三角形的内切圆
图片预览


文档简介
课件21张PPT。三角形的内切圆南城中学提出问题:
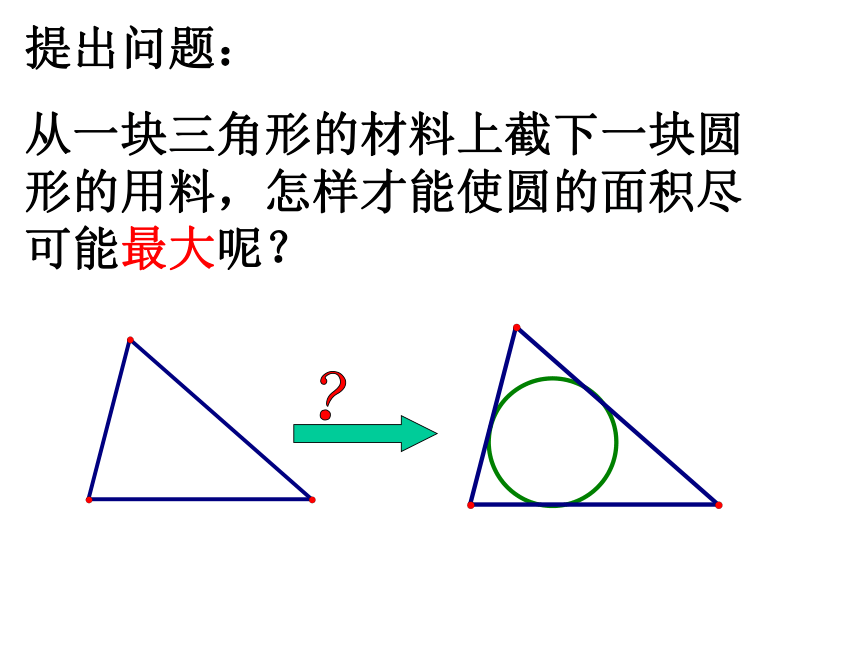
从一块三角形的材料上截下一块圆形的用料,怎样才能使圆的面积尽可能最大呢? 作圆: 使它和已知三角形的各边都相切已知:△ABC
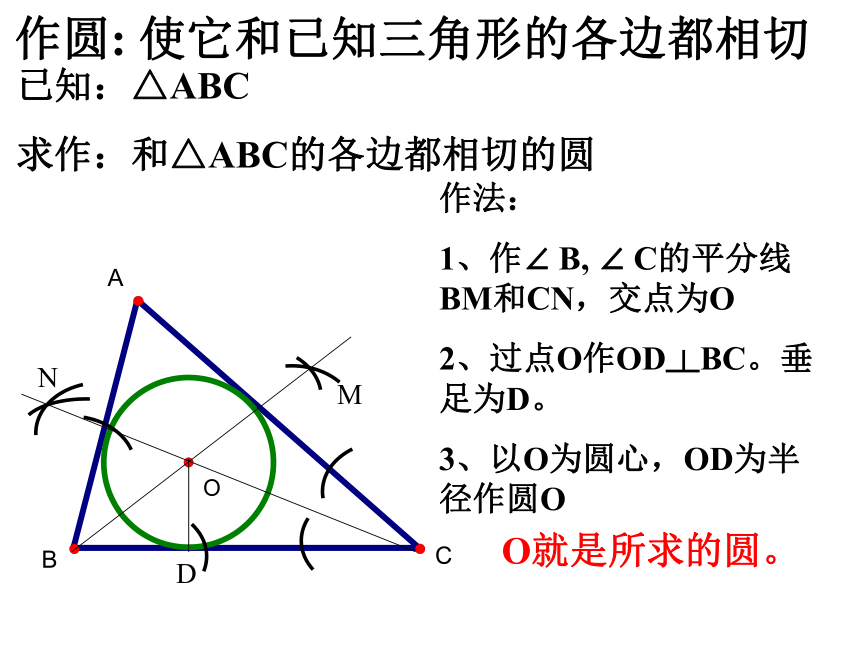
求作:和△ABC的各边都相切的圆O就是所求的圆。2、和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形。 概念;
1、和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。想一想:根据作法,和三角形各边都 相切的圆能作出几个? DEF1、什么是三角形的外接圆与内切圆?
2、如何画出一个三角形的外接圆与内切圆?画圆的关键:
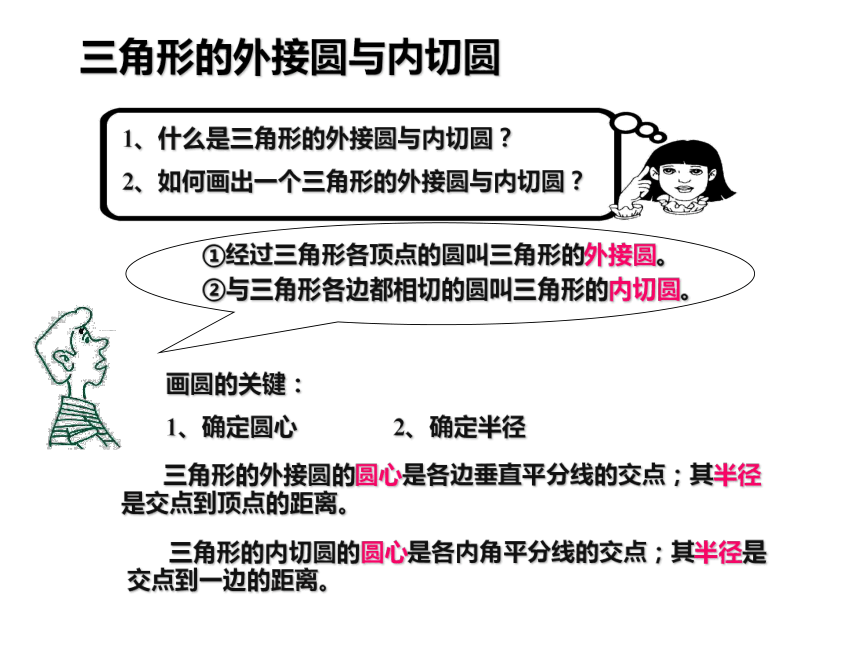
1、确定圆心 2、确定半径 三角形的外接圆的圆心是各边垂直平分线的交点;其半径是交点到顶点的距离。 三角形的内切圆的圆心是各内角平分线的交点;其半径是交点到一边的距离。三角形的外接圆与内切圆 ①经过三角形各顶点的圆叫三角形的外接圆。
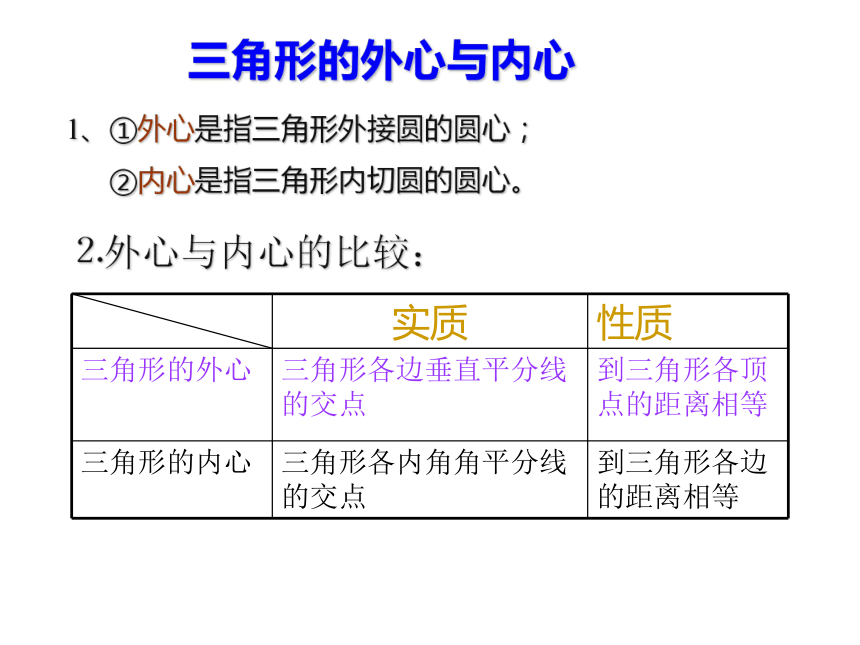
②与三角形各边都相切的圆叫三角形的内切圆。⒉外心与内心的比较:1、①外心是指三角形外接圆的圆心;
②内心是指三角形内切圆的圆心。三角形的外心与内心提示:关键是利用
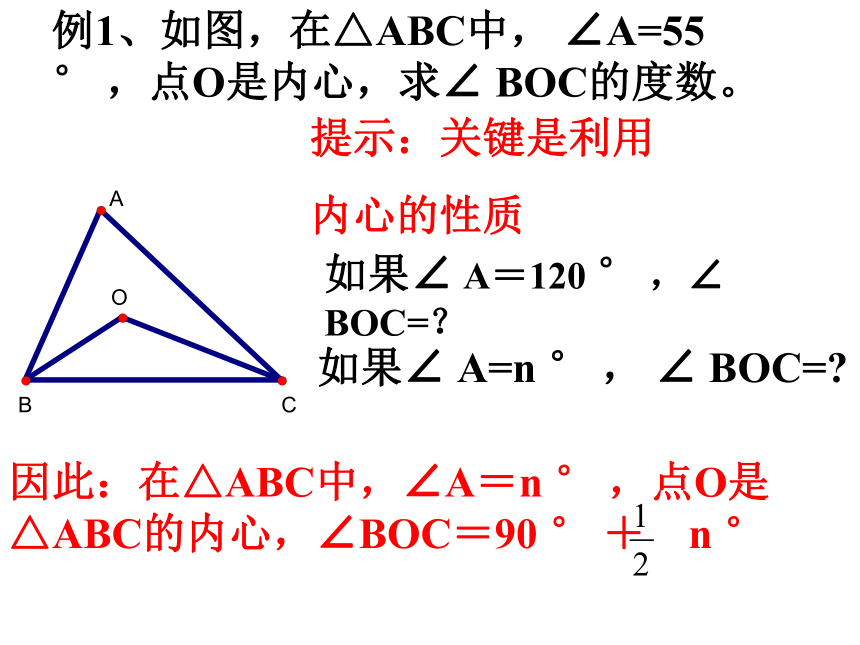
内心的性质如果∠ A=120 ° ,∠ BOC=?如果∠ A=n ° , ∠ BOC=?因此:在△ABC中,∠A=n ° ,点O是△ABC的内心,∠BOC=90 ° + n °例1、如图,在△ABC中, ∠A=55 ° ,点O是内心,求∠ BOC的度数。
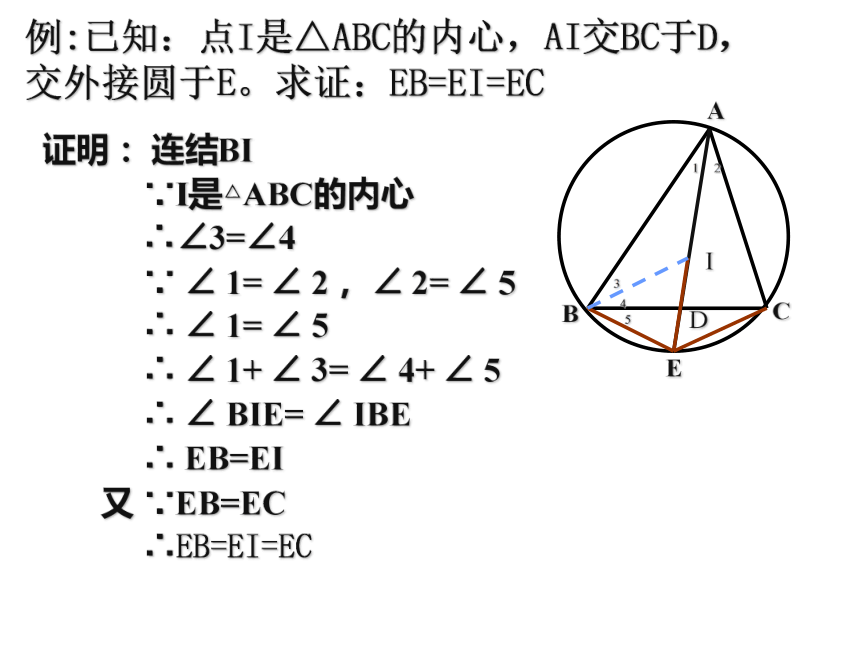
例:已知:点I是△ABC的内心,AI交BC于D,交外接圆于E。求证:EB=EI=EC
ABCIDE证明: 连结BI
∵I是△ABC的内心
∴∠3=∠4
∵ ∠ 1= ∠ 2, ∠ 2= ∠ 5
∴ ∠ 1= ∠ 5
∴ ∠ 1+ ∠ 3= ∠ 4+ ∠ 5
∴ ∠ BIE= ∠ IBE
∴ EB=EI
又 ∵EB=EC
∴EB=EI=EC
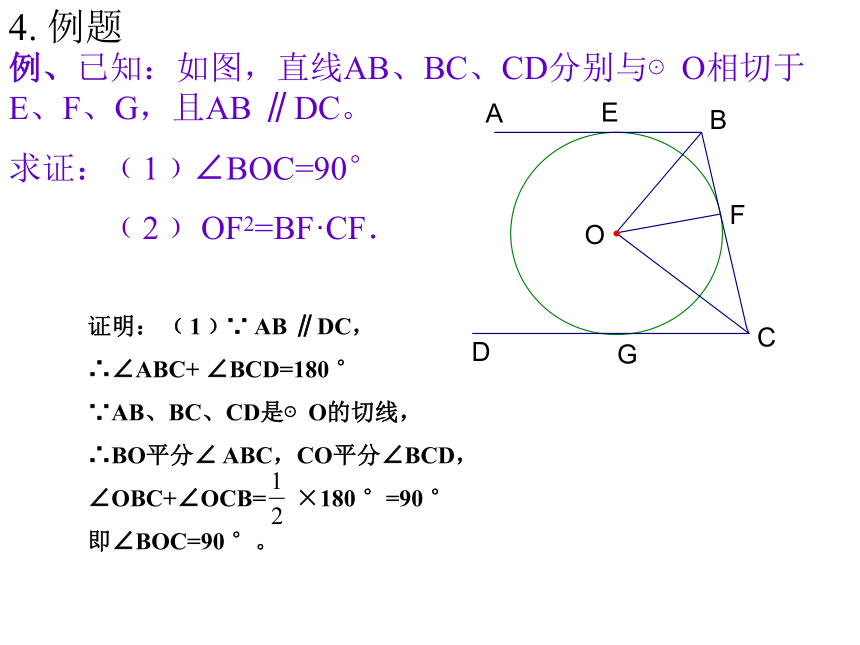
123454. 例题例、已知:如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB ∥DC。
求证:﹙1﹚∠BOC=90°
﹙2﹚ OF2=BF·CF.证明: ﹙1﹚∵ AB ∥DC,
∴∠ABC+ ∠BCD=180 °
∵AB、BC、CD是⊙O的切线,
∴BO平分∠ ABC,CO平分∠BCD,
∠OBC+∠OCB= ×180 °=90 °
即∠BOC=90 °。达标检测
一、判断。
1、三角形的外心到三角形各边的距离相等。 ( )
2、直角三角形的外心是斜边的中点。 ( )
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则它的外接圆
半径————,内切圆半径————。
2、等边三角形外接圆半径与内切圆半径之比————。
三、选择题:
下列命题正确的是( )
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆×√6.5cm2cm2:1C1、如图,⊙O是△ABC的内切圆,D、E、F是切点,∠A=50°,∠C=60°,则∠DOE=( )
(A)70° (B)110°
(C)120° (D)130° 2、等边三角形的内切圆半径、外接圆的半径和高的比为( )
(A)1∶ ∶ (B)1∶2∶
(C)1∶ ∶2 (D)1∶2∶3 巩固练习:ABCI1、如图,△ABC中,∠A=55度,I是内心
则,∠BIC=————度。ABCDEF2、如图,△ABC中,∠A=55度,其内切圆切△ABC 于D、E、F,则∠FDE=————度。
112.567.5课堂练习:
1、判断
(1)三角形的外心是三边中垂线的交点。( )
(2)三角形三边中线的交点是三角形内心。( )
(3)若O为△ABC的内心,
则OA=OB=OC。( )√××三个内角的角平分线的交点三边的距离相等ABCOI三、特殊三角形外接圆、内切圆半径的求法:R= —c2r = ————a+b-c2abc直角三角形外接圆、内切圆半径的求法若已知圆的三条切线呢?ABCDEF设△ABC的BC=a,CA=b,AB=c,内切圆I和BC、AC、AB分别相切于点D、E、F.Ixyzy+z=a
x+z=b
x+y=c分析:设 AF=x,BD=y,CE=z
例:已知在△ABC中,BC=14cm,AC=9cm,
AB=13cm,它的内切圆分别和BC、AC、
AB切于点D、E、F,求AF、BD和CE的长。xxyyzz已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。比一比
看谁做得快.ABCabcrr =a+b-c2例:直角三角形的两直角边分别是5cm,
12cm 则其内切圆的半径为______。OEF 练习2 已知:△ABC是⊙O外切三形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
? x+y=13
y+z=14
x+z=9课本第页 : 题。书山有路勤为径
从一块三角形的材料上截下一块圆形的用料,怎样才能使圆的面积尽可能最大呢? 作圆: 使它和已知三角形的各边都相切已知:△ABC
求作:和△ABC的各边都相切的圆O就是所求的圆。2、和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形。 概念;
1、和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。想一想:根据作法,和三角形各边都 相切的圆能作出几个? DEF1、什么是三角形的外接圆与内切圆?
2、如何画出一个三角形的外接圆与内切圆?画圆的关键:
1、确定圆心 2、确定半径 三角形的外接圆的圆心是各边垂直平分线的交点;其半径是交点到顶点的距离。 三角形的内切圆的圆心是各内角平分线的交点;其半径是交点到一边的距离。三角形的外接圆与内切圆 ①经过三角形各顶点的圆叫三角形的外接圆。
②与三角形各边都相切的圆叫三角形的内切圆。⒉外心与内心的比较:1、①外心是指三角形外接圆的圆心;
②内心是指三角形内切圆的圆心。三角形的外心与内心提示:关键是利用
内心的性质如果∠ A=120 ° ,∠ BOC=?如果∠ A=n ° , ∠ BOC=?因此:在△ABC中,∠A=n ° ,点O是△ABC的内心,∠BOC=90 ° + n °例1、如图,在△ABC中, ∠A=55 ° ,点O是内心,求∠ BOC的度数。
例:已知:点I是△ABC的内心,AI交BC于D,交外接圆于E。求证:EB=EI=EC
ABCIDE证明: 连结BI
∵I是△ABC的内心
∴∠3=∠4
∵ ∠ 1= ∠ 2, ∠ 2= ∠ 5
∴ ∠ 1= ∠ 5
∴ ∠ 1+ ∠ 3= ∠ 4+ ∠ 5
∴ ∠ BIE= ∠ IBE
∴ EB=EI
又 ∵EB=EC
∴EB=EI=EC
123454. 例题例、已知:如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB ∥DC。
求证:﹙1﹚∠BOC=90°
﹙2﹚ OF2=BF·CF.证明: ﹙1﹚∵ AB ∥DC,
∴∠ABC+ ∠BCD=180 °
∵AB、BC、CD是⊙O的切线,
∴BO平分∠ ABC,CO平分∠BCD,
∠OBC+∠OCB= ×180 °=90 °
即∠BOC=90 °。达标检测
一、判断。
1、三角形的外心到三角形各边的距离相等。 ( )
2、直角三角形的外心是斜边的中点。 ( )
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则它的外接圆
半径————,内切圆半径————。
2、等边三角形外接圆半径与内切圆半径之比————。
三、选择题:
下列命题正确的是( )
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆×√6.5cm2cm2:1C1、如图,⊙O是△ABC的内切圆,D、E、F是切点,∠A=50°,∠C=60°,则∠DOE=( )
(A)70° (B)110°
(C)120° (D)130° 2、等边三角形的内切圆半径、外接圆的半径和高的比为( )
(A)1∶ ∶ (B)1∶2∶
(C)1∶ ∶2 (D)1∶2∶3 巩固练习:ABCI1、如图,△ABC中,∠A=55度,I是内心
则,∠BIC=————度。ABCDEF2、如图,△ABC中,∠A=55度,其内切圆切△ABC 于D、E、F,则∠FDE=————度。
112.567.5课堂练习:
1、判断
(1)三角形的外心是三边中垂线的交点。( )
(2)三角形三边中线的交点是三角形内心。( )
(3)若O为△ABC的内心,
则OA=OB=OC。( )√××三个内角的角平分线的交点三边的距离相等ABCOI三、特殊三角形外接圆、内切圆半径的求法:R= —c2r = ————a+b-c2abc直角三角形外接圆、内切圆半径的求法若已知圆的三条切线呢?ABCDEF设△ABC的BC=a,CA=b,AB=c,内切圆I和BC、AC、AB分别相切于点D、E、F.Ixyzy+z=a
x+z=b
x+y=c分析:设 AF=x,BD=y,CE=z
例:已知在△ABC中,BC=14cm,AC=9cm,
AB=13cm,它的内切圆分别和BC、AC、
AB切于点D、E、F,求AF、BD和CE的长。xxyyzz已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。比一比
看谁做得快.ABCabcrr =a+b-c2例:直角三角形的两直角边分别是5cm,
12cm 则其内切圆的半径为______。OEF 练习2 已知:△ABC是⊙O外切三形,切点为D,E,F。若BC=14 cm ,AC=9cm,AB=13cm。求AF,BD,CE。
? x+y=13
y+z=14
x+z=9课本第页 : 题。书山有路勤为径
