第二十三章 旋转
图片预览


文档简介
第二十三章 旋 转
本章知识概览
[内容综述]
本章主要内容是图形的旋转,首先通过具体实例和现实生活中广泛存在的旋转现象对旋转有个初步认识,在此基础上进一步理解旋转的基本性质,并能作出简单平面图形旋转后的图形.
本章的重点是旋转的基本性质,并运用旋转的性质进行简单的旋转作图.
本章的难点是探索图形之间的变换关系以及旋转在现实生活中的应用.
[网络构建]
[学法指要]
1.学习本章要运用好观察、分析、归纳、概括的数学方法.旋转现象是现实生活中广泛存在的现象,学习本章就是从观察大量的生活中的旋转现象开始,直观地认识旋转,然后分析、归纳旋转的规律,最后概括出旋转的基本性质.
2.学习本章需要对图形进行观察和动手操作,学习时要充分利用这部分内容的特点经过大量的观察和动手操作等实践活动,积累丰富的数学活动经验,以形成良好的空间观念和一定的创新意识,同时在学习通过独立思考、自主探索和合作交流,进一步体会旋转的数学内涵.
3.学习本章要注重理解旋转概念和性质,而不能死记硬背,同时利用旋转的基本性质解释生活中的有关现象,在利用旋转的性质进行图案设计时要有不同的创新意识,对同一图案的分析要尽可能地提出不同的思路.
23.1图形的旋转
预习导航学案
[轻松启航]————————————————————————[激活思维]
1.在平面内,将一个图形绕一个定点沿某个方向如图23-1-1,如果把钟表的指针看作四边形
第二十三章 旋转
转动一个角度,这样的图形运动称为 ,这个定点称为 ,转动的角称为 ,旋转不改变图形的 .
2.经过旋转,图形上的每一点都绕 沿相同方向转动了 .任意一对对应点与旋转中心的连线所成的角都是 ,对应点到旋转中心的距离 ,旋转前后的图形 .
3.在旋转过程中,确定一个几何图形旋转后的位置,除需要此几何图形原来的位置外,还需要的条件是 和 .
4.把一个图案进行旋转,选择不同的 ,不同的 ,会出现不同效果.
AOBC,它绕点O按顺时针方向旋转到四边形DOEF,在这个旋转过程中:
(1)旋转中心是 ,旋转角是 .
(2)经过旋转,
点A、B分别移动
到什么位置?
(3)AO与DO的
长有什么关系?
BO与EO呢?
(4)∠AOD与∠BOE有什么大小关系?
互动研学教练
[教材研学]————————————————————————[举例说法]
一、对旋转概念的理解
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.这个定点叫旋转中心,转动的角度叫旋转解.
友情提示:(1)“将一个图形绕一个定点沿某个方向转动一个角度”,意味着图形上的每个点都按相同的方式转动相同的角度.
(2)旋转不改变图形的大小和形状.
二、旋转的性质
1.旋转后的图形与原图形的大小和形状不改变;
2.旋转前后两个图形的对应点到旋转中心的距离相等;
3.对应点到旋转中心的连线所成的角彼此相等.
1.作简单平面图形绕定点旋转一定角度后的图案,只要把平面图形上关键点都绕定点旋转一定角度,然后再按原来的式样连接这些点而成.
2.要确定一个简单平面图形旋转后的位置,除需要知道此平面图形原来位置外,还需要知道旋转中心和旋转角.
[例1]观察如图23-1-2所示的图
案,它可以看作是什么“基本图案”,
是通过怎样的旋转而得到的?
解:可以看作是一个“热带鱼”绕图案
的中心位置旋转600、1200、1800、2400、
3000形成的;也可以看作是相邻两个“热
带鱼”绕图案的中心位置旋转1200、2400形
成的;还可以看作是依次相邻的三个“热带
鱼”绕图案的中心位置旋转1800而形成的.
[例2]如图23-1-3,正方形
ABCD绕O点旋转后,顶点A的对应
点为A1,试确定B、C、D对应点的
位置,以及旋转后的正方形.
解:(1)连接OA1、OA、OB、OC、OD.
(2)如图23-1-4,分别以OB、OC、OD为一边作∠BOB1、∠COC1、∠DOD1,使得∠BOB1=∠COC1=∠DOD1=∠AOA1.
(3)分别在射线OB1、
OC1、OD1上截取OB1=OB、
OC1=OC、OD1=OD.
(4)连接B1C1、C1D1、
D1A1、A1B1.
正方形A1B1C1D1就
是正方形ABCD绕O点旋转后的图形.
点拨:假设顶点B、C、D的对应点分别为B1、C1、D1,则∠
BOB1、∠COC1、∠DOD1都是旋转角,且OB=OB1、OC=OC1、OD=
OD1 .
九年级数学(上)·人教版
中考真题在线
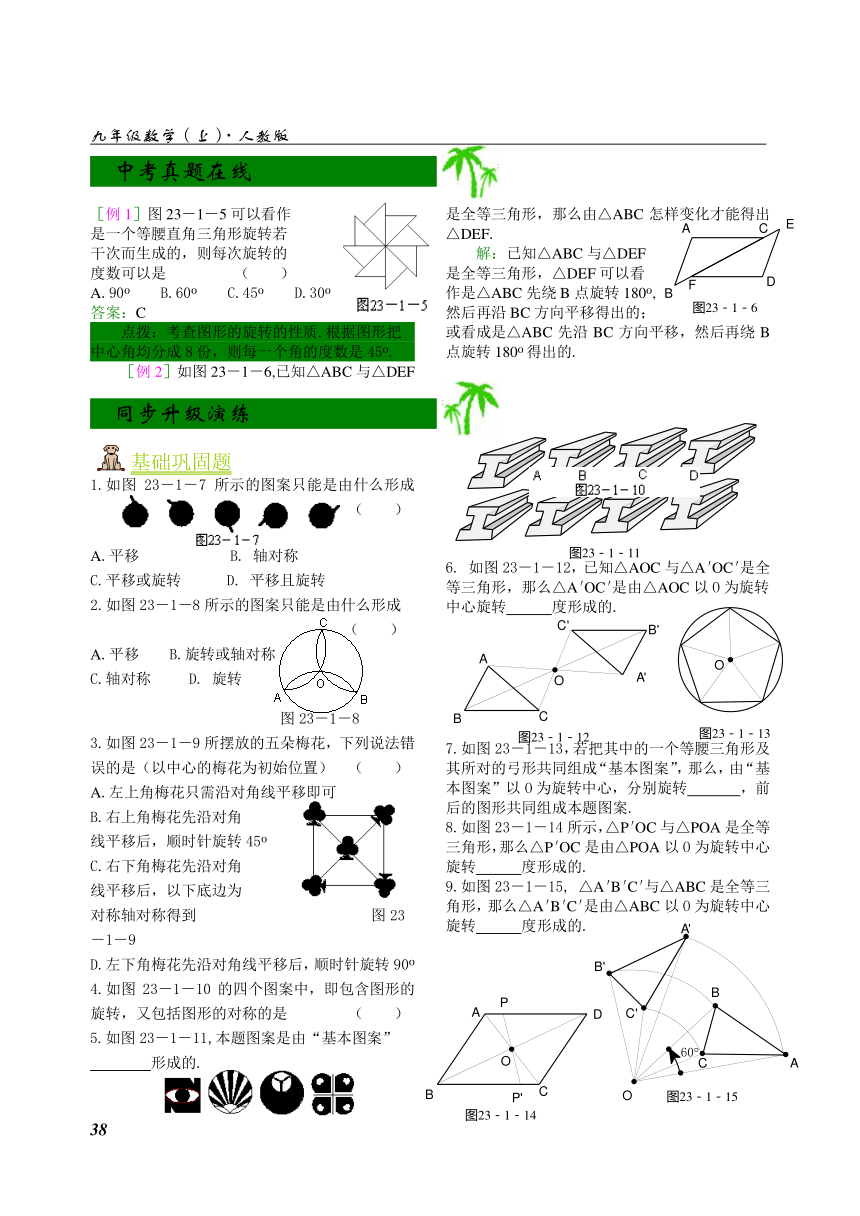
[例1]图23-1-5可以看作
是一个等腰直角三角形旋转若
干次而生成的,则每次旋转的
度数可以是 ( )
A.900 B.600 C.450 D.300
答案:C
点拨:考查图形的旋转的性质.根据图形把
中心角均分成8份,则每一个角的度数是450.
[例2]如图23-1-6,已知△ABC与△DEF是全等三角形,那么由△ABC怎样变化才能得出△DEF.
解:已知△ABC与△DEF
是全等三角形,△DEF可以看
作是△ABC先绕B点旋转1800,
然后再沿BC方向平移得出的;
或看成是△ABC先沿BC方向平移,然后再绕B点旋转1800得出的.
同步升级演练
基础巩固题
1.如图23-1-7所示的图案只能是由什么形成( )
A.平移 B. 轴对称
C.平移或旋转 D. 平移且旋转
2.如图23-1-8所示的图案只能是由什么形成( )
A.平移 B.旋转或轴对称
C.轴对称 D. 旋转
图23-1-8
3.如图23-1-9所摆放的五朵梅花,下列说法错误的是(以中心的梅花为初始位置) ( )
A.左上角梅花只需沿对角线平移即可
B.右上角梅花先沿对角
线平移后,顺时针旋转450
C.右下角梅花先沿对角
线平移后,以下底边为
对称轴对称得到 图23-1-9
D.左下角梅花先沿对角线平移后,顺时针旋转900
4.如图23-1-10的四个图案中,即包含图形的旋转,又包括图形的对称的是 ( )
5.如图23-1-11,本题图案是由“基本图案”
形成的.
6. 如图23-1-12,已知△AOC与△A′OC′是全等三角形,那么△A′OC′是由△AOC以O为旋转中心旋转 度形成的.
7.如图23-1-13,若把其中的一个等腰三角形及其所对的弓形共同组成“基本图案”,那么,由“基本图案”以O为旋转中心,分别旋转 ,前后的图形共同组成本题图案.
8.如图23-1-14所示,△P′OC与△POA是全等三角形,那么△P′OC是由△POA以O为旋转中心旋转 度形成的.
9.如图23-1-15, △A′B′C′与△ABC是全等三角形,那么△A′B′C′是由△ABC以O为旋转中心旋转 度形成的.
第二十三章 旋转
探究提高题
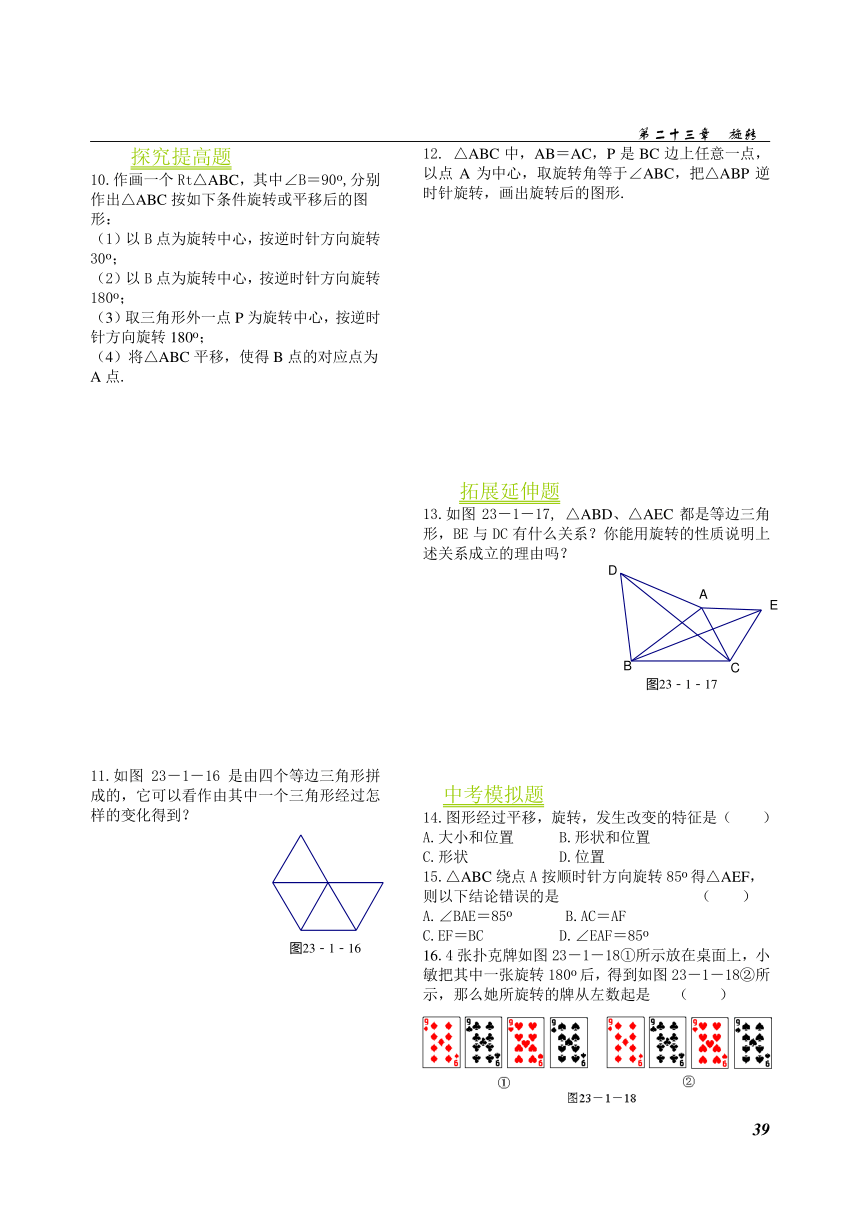
10.作画一个Rt△ABC,其中∠B=900,分别作出△ABC按如下条件旋转或平移后的图形:
(1)以B点为旋转中心,按逆时针方向旋转300;
(2)以B点为旋转中心,按逆时针方向旋转1800;
(3)取三角形外一点P为旋转中心,按逆时针方向旋转1800;
(4)将△ABC平移,使得B点的对应点为A点.
11.如图23-1-16是由四个等边三角形拼成的,它可以看作由其中一个三角形经过怎样的变化得到?
12. △ABC中,AB=AC,P是BC边上任意一点,以点A为中心,取旋转角等于∠ABC,把△ABP逆时针旋转,画出旋转后的图形.
拓展延伸题
13.如图23-1-17, △ABD、△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
中考模拟题
14.图形经过平移,旋转,发生改变的特征是( )
A.大小和位置 B.形状和位置
C.形状 D.位置
15.△ABC绕点A按顺时针方向旋转850得△AEF,则以下结论错误的是 ( )
A.∠BAE=850 B.AC=AF
C.EF=BC D.∠EAF=850
16.4张扑克牌如图23-1-18①所示放在桌面上,小敏把其中一张旋转1800后,得到如图23-1-18②所示,那么她所旋转的牌从左数起是 ( )
九年级数学(上)·人教版
23.2中心对称
预习导航学案
[轻松启航]————————————————————————[激活思维]
1.如图23-2-1,线段AC、BD相
交于点O,OA=OC,OB=OD,把
△OCD绕点O旋转1800,则△OCD
与△OAB .
2.把一个图形绕着某一个点旋转1800后,如果它能够与另一个图形重合,那么就说这两个图形关于这个点 或 ,这个点叫做 ,这两个图形中的对应点叫做 .
3.关于中心对称的两个图形,对称点所连线段都经过 ,而且 .
4.关于中心对称的两个图形是 .
5.把一个图形绕某一个点旋转1800,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做 ,这个点是 .
6.线段绕它的中点旋转1800后,它的两个端点互换了位置,旋转后的线段和 重合,因此,线段是 , 是它的对称中心.
7.两个点关于原点对称时,它们的坐标 相反,即点关于原点的对称点为 .
1.□ABCD中,点O 是对角线的交点,因为OA=OC,OB=OD,所以图形绕点O旋转 后,点A与点C,点B与点D分别互换了位置,旋转后的图形和原来的图形重合,因此平行四边形是 ,
是它的对称中心.
2.等边三角形是中心对称图形吗?为什么?
3.已知点A(a,1)与点A′(5,b)关于原点O的对称点,那么a、b是多少?
互动研学教练
[教材研学]————————————————————————[举例说法]
一、中心对称和中心对称图形的区别与联系
中心对称和中心对称图形是两个不同而又紧密联系的概念.
1.区别:中心对称是指两个全等图形之间的相互位置关系,这两个图形关于一点对称,这个点是对称中心,两个图形关于一点对称也叫中心对称.成中心对称的两个图形中,其中一个图形上所有点关于对称中心的对称点都在另一个图形上,反之,另一个图形上所有点的对称点,又都在这个图形上;而中心对称图形是指图形本身成中心对称,中心对称图形上所有点关于对称中心的对称点都在这个图形本身上.
2.联系:如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形;一个
[例1]如图23-2-2, □ABCD的对角线相交于O,E、F在直线BD上,且BE=DF,
说出图中:
(1)四边形AECF是不
是中心对称图形,说出理由.
(2)四边形AECF的对
称中心是什么?
解:(1)四边形AECF是中心对称图形.理由是:因为□ABCD对角线互相平分,所以OA=OC,OB=OD.而BE=DF,因此OB+BE=OD+DF,即OE=OF.由对角线互相平分的四边形是平行四边形,因此四边形AECF是平行四边形,故四边形AECF是中心对称图形.
(2)平行四边形AECF的对称中心是对角线交点O.
[例2]如图23-2-3中的扑克牌中,哪些牌的牌面是中心对称图形?
第二十三章 旋转
中心对称图形,如果把对称的部分看成两个图形,那么它们又是关于中心对称.
二、关于原点对称的坐标
两个点关于原点对称时,它们的坐标符号相反,即点P(a,b)关于原点的对称点为
友情提示:两个点关于原点对称的点的坐标特点一定要与两个点关于x轴或y轴对称的点的坐标特点区别开,两个点关于x轴对称时,它们的横坐标相同,纵坐标符号相反;两个点关于y轴对称时,它们的横坐标符号相反,纵坐标相同,即点P(a,b)关于x轴对称的点P1(a,-b),关于y轴对称的点P2(-a,b).
解:①②为中心对称图形.
点拨:考查中心对称图形,要注意区分每张扑
克牌中的小图案的方向,培养学生严谨的学习态度.
[例3]已知
解:由题意,得
点拨:根据关于原点对称的点的坐标特点,它
们的坐标符号相反,可得
解得a=-,b=4
中考真题在线
[例1] 下列图形中,不是中心对称的是 ( )
A.圆 B.菱形 C.矩形 D.等边三角形
答案:D
点拨:根据中心对称的定义,绕某个点旋转 1800后,旋转后的图形能够重合,故根据定义, 知不是中心对称的是D.
[例2]等边三角形、正方形、菱形、等腰梯形这四种图形中,是中心对称图形的有 ( )
A.1个 B.2个 C.3个 D.4个
答案:B.
点拨:根据中心对称的定义,知正方形、
菱形是中心对称图形,故应选B.
[例3]如图23-2-4,等腰梯形ABCD中,ABCD,AB=2CD,AC交BD于点O,点E、F分别为AO、BO的中点,则下
列关于点O成中心对称
的一组三角形是( )
A.△ABO与△CDO
B.△AOD与△BOC
C.△COD与△EOF
D.△ACD与△BCD
答案:C
点拨:根据中心对称的定义易得.
同步升级演练
基础巩固题
1.下列几何图形中,是中心对称图形而不是轴对称图形的是 ( )
A.等边三角形 B.矩形
C.平行四边形 D.菱形
2.国旗上的每个五角星 ( )
A.是中心对称图形而不是轴对称图形
B.是轴对称图形而不是中心对称图形
C.既是中心对称图形,又是轴对称图形
D.既不是中心对称图形,又不是轴对称图形
3.在等边三角形、平行四边形、正方形和线段四种图形中,既是轴对称图形,又是中心对称图形的有 ( )
A.1种 B.2种 C.3种 D.4种
4.在等腰三角形、等边三角形、平行四边形、矩形、正方形和圆六种图形中,是中心对称图形,而不轴对称图形的有 ( )
A.1种 B.2种 C.3种 D.6种
5.四边形ABCD对角线相交于O,且OA=OB=OC=OD,则这个四边形 ( )
A.仅是轴对称图形
B.仅是中心对称图形
C.既不是中心对称图形,又不是轴对称图形
D.既是中心对称图形,又是轴对称图形
6.图23-2-5中,既是中心对称图形,又是轴对称图形的是 ( )
九年级数学(上)·人教版
7. 图23-2-6中,是中心对称图形的是 ( )
8.中心对称图形上,每一对对称点连成的线段都被 平分.
9.平行四边形是 对称图形,矩形、菱形和正方形不仅是 图形,而且也是 图形.
10.过平行四边形对角线的交点任作一条直线与两边相交(或与两边延长线相交),交点到对角线交点的距离 ,这是因为平行四边形是 .
11.将正方形绕对称中心旋转 后,与原来位置重合.
12.如图23-2-7所示,观察图案并回答下列问题:
(1)图案是不是轴对称图形,如果是,图案有几条对称轴?
(2)图案是不是中心对称图形,为什么?找出对称中心.
(3)图案绕中心旋转多少度能和原来的图案重合?
探究提高题
13.仔细观察如图23-2-8,所列26英文字母,将相应的字填入表格中适当的空格内.
对称 中心对称图形 轴对称图形
只有一对称轴 有两条对称轴
英文字母
14.经过矩形的对称中心任作一直线能否将矩形平分为面积相等的两部分?说明理由.
拓展延伸题
15.如图23-2-9甲所示,魔术师把4张扑克牌放在桌上,然后蒙上眼睛,请一位观众上台,把某一张牌旋转1800,魔术师解除蒙具后,看到4张扑克牌如图23-2-9乙所示,他很快确定了哪一张牌被旋转过,请问:魔术师所指的哪一张牌被旋转过了?他是怎么知道的?
16.观察如图23-2-10中的甲、乙两图,回答下列问题:
甲
乙
图23-2-10
(1)它们是不是轴对称图形、中心对称图形?请分别加以说明.
(2)如果是轴对称图形找出对称轴,如果中心对称图形找出对称中心.
第二十三章 旋转
中考模拟题
17.(2006年·北京宣武质检)图形:①线段;②正五角星;③相交两圆(非等圆);④双曲线.其中是轴对称图形而不是中心对称图形的是( )
A.①③④ B.①③
C.②③ D.③④
18.(2006年·南昌测试)图23-2-11中的图案是几种名车标志,其中是中心对称图形的共( )
A.1个 B.2个 C.3个 D.4个
23.3课题学习 图案设计
23.3课题学习 图案设计
预习导航学案
[轻松启航]————————————————————————[激活思维]
1.在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为 ,平移不改变图形的 和 .
2.经过平移,对应点所连的线段 且 ,对应线段 且 ,对应角 .
3.经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了 ,任意一对对应点与旋转中心的连线所成的角都是 ,对应点到旋转中心的距离 .
4.把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线 ,这条直线叫做 ,两个图形关于直线对称也叫做 .
5.关于某条直线对称的两个图形是 .
1.观察图案23-3-1,可以看作由什么“基本图案”经过怎样的变换形成的?
2.如图23-3-2的图案可以看作是以一个怎样的图案为“基本图案”形成的?试用两种以上的方法分析它的形成过程.
互动研学教练
[教材研学]————————————————————————[举例说法]
一、运用平移、旋转、轴对称等知识对生活中见到的一些美丽的图案分析其形成过程
对生活中的图案,运用平移、旋转、轴对称的观点分析其形成过程,关键是在图案中找到“基本图案”,并运用平移、旋转、轴对称的组合进行变化,检验是否形成给出图案.
二、运用平移、旋转、轴对称进行图案设计
[例1]欣赏如图23-3-3的图案,
并分析图案的形成过程.
解:图案是由图形的四分之一,即四
根J形的“基本图案”,绕图形中心向同
一方向旋转900、1800、2700而形成的.
[例2]利用23-3-4所给图形进行图
案设计,并说明设计的含义.
解:如图23-3-5所示.
九年级数学(上)·人教版
运用平移、旋转、轴对称进行图案设计,首先要选择基本图形,然后制定设计思路,再遵照平移、旋转或轴对称的基本操作对基本图形及其组合进行变化,便可得到相应的图案.
点拨:图案设计就是运用变化图形的方法—
—平移、旋转和轴对称对基本图案进行适当的变
形,组成具有一定意义的新图形.
中考真题在线
[例1](2004年·南安)如图23-3-6,△ABC、△ADE均是顶角为420的等腰
三角形,BC、DE分别是底边,
图中的哪两个三角形可以通
过怎样的旋转而相互得到?
解:△ABC与△ADE可以
通过以点A为旋转中心的旋
转变换而相互得到,旋转角度为420.
[例2](2004年·嘉兴)如图23-3-7,过正方形的中心O点和边上一点P随意连一条曲线,将所画的曲线绕O点按同一方向连续旋转三次,每次的旋转角都是900,这样就将正方
形分成了四部分,这四部分之间
有什么关系?
解:这四部分是大小,形状完全
相同的四块图案.
同步升级演练
基础巩固题
1.利用平移分析图23-3-8中“三鸟”商标的图案(不考虑汉字),并设计一个你所喜欢的徽标图案.
2.利用轴对称分析图23-3-9中“钢鹰”商标的图案(不考虑汉字),并设计一个你喜欢的商标图案.
3.利用旋转分析图23-3-10中“三蝶”商标的图案(不考虑汉字),并设计一个你喜欢的商标图案.
探究提高题
4. 利用旋转和轴对称分析图23-3-11中的图案的形成过程.
第二十三章 旋转
5. 利用平移、旋转和轴对称分析图23-3-11中花边图案的形成过程.
拓展延伸题
6.利用角、线段等基本图形,借助旋转、平移或轴对称设计一个图案,并简述你的设计意图.
7.图23-3-13是一个由“树叶”状图形组成的图案,利用平移、轴对称或旋转分析这个图案的形成过程.
中考模拟题
8.(2006年·南京质检)如图23-3-15的图案中,由图23-3-14经过平移得到的是( )
九年级数学(上)·人教版
第二十二章质量评估
(时间:100分钟 满分:120分)
一、选择题(每小题4分,共24分)
1.在图23-2中,是由图23-1
通过平移得到的图形是 ( )
2.△ABC绕A点按顺时针方向旋转850,得△AEF则以下结论错误的是 ( )
A.∠BAE=850 B.AC=AF
C.EF=BC D.∠EAF=850
3.如图23-3所示,O是正六边形ABCDEF的中点,下列图形中可由△OBC
平移得到的是 ( )
A.△OCD
B.△OAB
C.△OAF
D.△OEF
4.(2005年·烟台)4根火柴棒形成如图23-4所示的象形“口”字,平移火柴棒后,原图形能变成的象形汉字是图23-5中的 ( )
5.在综合实践活动课上,
小红准备用两种不同颜色的布
料缝制一个正方形坐垫,坐垫
图案如图23-6所示,应该选
图23-7中的哪一块布料才能
使其与图23-6拼接符合原来
的图案模式 ( )
6.一电动玩具的正面是由
半径为10cm的小圆盘和半径
为20cm的大圆盘依图23-8
方式连接而成的,小圆盘在大
圆盘的圆周上外切,滚动一周
且不发生滑动(大圆盘不动),
回到原来的位置,在这一过程
中,判断虚线所示位置的三个圆内,图23-9所画的头发、眼睛、嘴巴位置正确的是( )
二、填空题:(每小题3分,共27分)
7.图23-10①②③④⑤⑥⑦中, 是由①平移得出的, 是由平移且旋转得出的.
8.如图23-11所示,已知矩形EFMN是由矩形ABCD经过平移而得到的,AB-1,∠EMF=300,则EM= ,∠ACB= ,矩形EFMN的面积= 。
9.如图23-12所示,
把正方形ABCD沿着对角线
AC的方向平移到正方形A′B′
C′D′的位置,它们的重叠部
分的面积是正方形ABCD的
面积的一半,若AC=,则
正方形移动的距离AA′是 .
10.如图23-13所示的
图案可以看作是一个正方形
经过 次旋转得到的,
每次旋转 .
11.皮皮与毛毛玩一种游
戏,他们要将图23-14中的
图(1)和图(2)中的三角形通过水平或竖直平移的方法得到图(3),平移过程中,每次水平或竖直平稳一个格,先拼完的为胜;皮皮选择了图(1),毛毛选择了图(2),那么 将获胜.
第二十三章 旋转
12.如图23-15所示,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有 个不同的四边形.
13.将5cm长的线段MN向右平移3cm得到线段PQ,则PQ的长度等于 cm,将MN绕平面内一点O旋转1000,得到线段EF,则线段EF的长度等于 cm.
14.将面积为12cm2的正方形ABCD,向上平移5cm得到图形FEGH,则图形EFGH是 形,面积等于 cm2.
15.已知=900,将∠ABC绕平面内一点O旋转300,得到∠EFG,则∠EFG的度数为 .
三、解答题(共66分)
16.(12分)(1)如图23-16,(甲),在方格纸中如何通过平移或旋转这两种变换,由图形A得到图形B,再由图形B得到图形C(对于平移变换要求回答出平移的方向和平移的距离,对于旋转变换要求回答出旋转中心、旋转方向和旋转角度);
(20如图23-16(甲),如果点P、点P3的坐标分别为(0,0)、(2,1),写出点P2的坐标;
(3)如图23-16(乙)是某设计师设计图案的一部分,请你运用旋转变换的方法,在方格纸中将图形绕点O顺时针依次旋转900,1800,2700,依次画出旋转后所得到的图形,你会得到一个美丽的图案,但涂阴影时不要涂错了位置,否则不会出现理想的效果,你来试一试吧!
注:方格纸中的小正方形的边长为1个单位长度.
17.(12分)将图23-17方格中的图案作下列变换,请画出相应的图案;
(1)沿y轴正向平移4个单位;
(2)关于y轴轴对称.
18.(8分)经过平移,图23-18的图形上A点移到E点,作出平移后的图形.
19.(10分)在图23-19中,将ABCO绕O点按顺时针方向分别旋转900,1800,2700,并将相应的△OBC部分涂上阴影,观察所得的图案.
九年级数学(上)·人教版
20.(12分)如图23-20所示,A点坐标为(3,3),将△ABC先向下平移4个单位得△A′B′C′,再将△A′B′C′绕点O逆时针旋转1800得△A′′B′′C′′.请你画出△A′B′C′和△A′′B′′C′′,并写出点A′′的坐标.
21.(12分)观察如图23-21所示图案,(1)它是由怎样的“基本图案”经过旋转而形成的?
(2)如果运用旋转和轴对称的组合,它又是由怎样的“基本图案”通过轴对称和旋转而成?
(3)如果仅用轴对称,它又是由怎样的“基本图案”经过几次轴对称而形成?
期中标准评估
期中标准评估
(时间:100分钟 满分:120分)
一、选择题(每小题4分,共24分)
1.下列各式正确的是 ( )
A.()2=-3 B. =3
C. =-3 D. (-)2=3
2.计算(-)2007·( + )2006的结果为 ( )
A.- B. +
C.-1 D.--
3.计算-(1-)是 ( )
A.3-1 B. 3+1
C.-1 D.+1
4.若1<x<2,则| x-3|+ 的值( )
A.2 x-4 B.-2
C.4-2 x D.2
5.已知3是关于x的方程x2-2a+1=0的一个根,则2 a的值是 ( )
A.11 B.12 C.13 D.14
6.一元二次方程2x2+3x-4=0的根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.不能确定
7.用配方法解关于x的方程x2-px+ q=0,此方程可变形为 ( )
A.( x + )2= B. ( x + )2=
C.( x-)2= D. ( x-)2=
8.一批上衣原价每件240元,经两次降价后每件194.4元,如果每次降价的百分数相同,则每次降价的百分率为 ( )
A.10% B.9% C.8% D.7%
9.如图Z-1所示是一只停泊在平静湖面上的小船,它的“倒影”是图Z-2中的 ( )
10.在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,图Z-3中,不能由一个基本图形通过旋转得到的是 ( )
二、填空题:(每小题3分,共27分)
11.方程(m-1) x|m|+1-2x=3是关于x的一元二次方程,则m= .
12.三角形两边长分别为2和4,第三边是方程x2-4x+3=0的解,则这个三角形的周长为 .
13. x2+5x+2=0的解为 .
14.若|x-3|+(x-y+1)2=0,则= .
15.如图Z-4所示,在
△ABC中,∠C=900,AC=2cm,
把这个三角形在平面内绕点所
走过的路线长是 cm.
16.如图Z-5,边长为
3的正方形ABCD绕点C顺
时针旋转300后得到正方形
EFCG,EF交AD于点H,那么
DH的长为 .
17.两个数的差是2,它们的
平方和是52,则这两个数为
.
18.函数y= +的自变量x的取值范围是 .
三、解答题(共74分)
19.(10分)解下列方程:
(1)3x2+5x=2;
(2)4(x+2)2=25(x-2)2.
九年级数学(上)·人教版
20.(6分)已知y=++18,求代数式-的值.
21.(10分)观察下列各式及其验证过程:
2=.
验证:2==
==.
3=.
验证:3==
==.
(1)按照上述两个等式及其验证过程的基本思想,猜想4的变形结果并进行验证.
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
22.(10分)如图Z-6,在Rt△ABC中,∠C=900,BC=4,AC=4,现将△ABC沿CB方向平移到△A′B′C′的位置.
(1)若平移的距离为3,求△ABC与△A′B′C′重叠部分的面积.
(2)若平移的距离为x(0≤x≤4),求△ABC与△A′B′C′重叠部分的面积y,列出y与x的关系式.
23.(8分)某商店如果将进货价为8元的商品按每件10元出售,每天可销售200件,现采用提高售价,减少进货量方法增加利润,已知这种商品每涨价0.5元,其销售量就减少10件,问应将销售价定为多少时,才能使所赚利润达到720元?这种商品的利润可以达到800元吗?为什么
期中标准评估
24.(10分)读下列解题过程:
题目:已知方程x2+3x+1=0的两个根为α、β,求 + 的值.
解:因为△=32-4×1×1=5>0,所以α≠β.(1)由一元二次方程根与系数的关系,得α+β=-3, αβ=1.(2)
所以 + = + = = =-3.(3)
阅读后回答问题:
上面的解题过程是否正确?若不正确,指出错在哪一步,并写出正确的解题过程.
25.如图Z-7(1)所示,已知两全等正方形ABCD与ABCD,正方形ABCD的顶点C与正方形的中心重合,且绕点C旋转.
(1)当正方形ABCD由图Z-7(1)位置旋转至图Z-7(2)位置时,两个正方形重叠部分的面积是否相等?说明理由.
(2)当正方形ABCD旋转至任意位置旋转至图Z-7(3)时,两个正方形重叠部分的面积会怎样变化?说明你的结论.
26.某商店进了一批服装,进货单价为50元,如果按每件60元出售,可销售800件,如果每件提价1元出售,其销量就减少20件,现在要获利12000元,且销售成本不超过24000元,问这种服装销售单价确定多少为宜,这时应进多少服装?
a+1=-(2a+1),
2b-3=―(―b-1).
a+1=-(2a+1),
2b-3=b+1.
PAGE
47
本章知识概览
[内容综述]
本章主要内容是图形的旋转,首先通过具体实例和现实生活中广泛存在的旋转现象对旋转有个初步认识,在此基础上进一步理解旋转的基本性质,并能作出简单平面图形旋转后的图形.
本章的重点是旋转的基本性质,并运用旋转的性质进行简单的旋转作图.
本章的难点是探索图形之间的变换关系以及旋转在现实生活中的应用.
[网络构建]
[学法指要]
1.学习本章要运用好观察、分析、归纳、概括的数学方法.旋转现象是现实生活中广泛存在的现象,学习本章就是从观察大量的生活中的旋转现象开始,直观地认识旋转,然后分析、归纳旋转的规律,最后概括出旋转的基本性质.
2.学习本章需要对图形进行观察和动手操作,学习时要充分利用这部分内容的特点经过大量的观察和动手操作等实践活动,积累丰富的数学活动经验,以形成良好的空间观念和一定的创新意识,同时在学习通过独立思考、自主探索和合作交流,进一步体会旋转的数学内涵.
3.学习本章要注重理解旋转概念和性质,而不能死记硬背,同时利用旋转的基本性质解释生活中的有关现象,在利用旋转的性质进行图案设计时要有不同的创新意识,对同一图案的分析要尽可能地提出不同的思路.
23.1图形的旋转
预习导航学案
[轻松启航]————————————————————————[激活思维]
1.在平面内,将一个图形绕一个定点沿某个方向如图23-1-1,如果把钟表的指针看作四边形
第二十三章 旋转
转动一个角度,这样的图形运动称为 ,这个定点称为 ,转动的角称为 ,旋转不改变图形的 .
2.经过旋转,图形上的每一点都绕 沿相同方向转动了 .任意一对对应点与旋转中心的连线所成的角都是 ,对应点到旋转中心的距离 ,旋转前后的图形 .
3.在旋转过程中,确定一个几何图形旋转后的位置,除需要此几何图形原来的位置外,还需要的条件是 和 .
4.把一个图案进行旋转,选择不同的 ,不同的 ,会出现不同效果.
AOBC,它绕点O按顺时针方向旋转到四边形DOEF,在这个旋转过程中:
(1)旋转中心是 ,旋转角是 .
(2)经过旋转,
点A、B分别移动
到什么位置?
(3)AO与DO的
长有什么关系?
BO与EO呢?
(4)∠AOD与∠BOE有什么大小关系?
互动研学教练
[教材研学]————————————————————————[举例说法]
一、对旋转概念的理解
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.这个定点叫旋转中心,转动的角度叫旋转解.
友情提示:(1)“将一个图形绕一个定点沿某个方向转动一个角度”,意味着图形上的每个点都按相同的方式转动相同的角度.
(2)旋转不改变图形的大小和形状.
二、旋转的性质
1.旋转后的图形与原图形的大小和形状不改变;
2.旋转前后两个图形的对应点到旋转中心的距离相等;
3.对应点到旋转中心的连线所成的角彼此相等.
1.作简单平面图形绕定点旋转一定角度后的图案,只要把平面图形上关键点都绕定点旋转一定角度,然后再按原来的式样连接这些点而成.
2.要确定一个简单平面图形旋转后的位置,除需要知道此平面图形原来位置外,还需要知道旋转中心和旋转角.
[例1]观察如图23-1-2所示的图
案,它可以看作是什么“基本图案”,
是通过怎样的旋转而得到的?
解:可以看作是一个“热带鱼”绕图案
的中心位置旋转600、1200、1800、2400、
3000形成的;也可以看作是相邻两个“热
带鱼”绕图案的中心位置旋转1200、2400形
成的;还可以看作是依次相邻的三个“热带
鱼”绕图案的中心位置旋转1800而形成的.
[例2]如图23-1-3,正方形
ABCD绕O点旋转后,顶点A的对应
点为A1,试确定B、C、D对应点的
位置,以及旋转后的正方形.
解:(1)连接OA1、OA、OB、OC、OD.
(2)如图23-1-4,分别以OB、OC、OD为一边作∠BOB1、∠COC1、∠DOD1,使得∠BOB1=∠COC1=∠DOD1=∠AOA1.
(3)分别在射线OB1、
OC1、OD1上截取OB1=OB、
OC1=OC、OD1=OD.
(4)连接B1C1、C1D1、
D1A1、A1B1.
正方形A1B1C1D1就
是正方形ABCD绕O点旋转后的图形.
点拨:假设顶点B、C、D的对应点分别为B1、C1、D1,则∠
BOB1、∠COC1、∠DOD1都是旋转角,且OB=OB1、OC=OC1、OD=
OD1 .
九年级数学(上)·人教版
中考真题在线
[例1]图23-1-5可以看作
是一个等腰直角三角形旋转若
干次而生成的,则每次旋转的
度数可以是 ( )
A.900 B.600 C.450 D.300
答案:C
点拨:考查图形的旋转的性质.根据图形把
中心角均分成8份,则每一个角的度数是450.
[例2]如图23-1-6,已知△ABC与△DEF是全等三角形,那么由△ABC怎样变化才能得出△DEF.
解:已知△ABC与△DEF
是全等三角形,△DEF可以看
作是△ABC先绕B点旋转1800,
然后再沿BC方向平移得出的;
或看成是△ABC先沿BC方向平移,然后再绕B点旋转1800得出的.
同步升级演练
基础巩固题
1.如图23-1-7所示的图案只能是由什么形成( )
A.平移 B. 轴对称
C.平移或旋转 D. 平移且旋转
2.如图23-1-8所示的图案只能是由什么形成( )
A.平移 B.旋转或轴对称
C.轴对称 D. 旋转
图23-1-8
3.如图23-1-9所摆放的五朵梅花,下列说法错误的是(以中心的梅花为初始位置) ( )
A.左上角梅花只需沿对角线平移即可
B.右上角梅花先沿对角
线平移后,顺时针旋转450
C.右下角梅花先沿对角
线平移后,以下底边为
对称轴对称得到 图23-1-9
D.左下角梅花先沿对角线平移后,顺时针旋转900
4.如图23-1-10的四个图案中,即包含图形的旋转,又包括图形的对称的是 ( )
5.如图23-1-11,本题图案是由“基本图案”
形成的.
6. 如图23-1-12,已知△AOC与△A′OC′是全等三角形,那么△A′OC′是由△AOC以O为旋转中心旋转 度形成的.
7.如图23-1-13,若把其中的一个等腰三角形及其所对的弓形共同组成“基本图案”,那么,由“基本图案”以O为旋转中心,分别旋转 ,前后的图形共同组成本题图案.
8.如图23-1-14所示,△P′OC与△POA是全等三角形,那么△P′OC是由△POA以O为旋转中心旋转 度形成的.
9.如图23-1-15, △A′B′C′与△ABC是全等三角形,那么△A′B′C′是由△ABC以O为旋转中心旋转 度形成的.
第二十三章 旋转
探究提高题
10.作画一个Rt△ABC,其中∠B=900,分别作出△ABC按如下条件旋转或平移后的图形:
(1)以B点为旋转中心,按逆时针方向旋转300;
(2)以B点为旋转中心,按逆时针方向旋转1800;
(3)取三角形外一点P为旋转中心,按逆时针方向旋转1800;
(4)将△ABC平移,使得B点的对应点为A点.
11.如图23-1-16是由四个等边三角形拼成的,它可以看作由其中一个三角形经过怎样的变化得到?
12. △ABC中,AB=AC,P是BC边上任意一点,以点A为中心,取旋转角等于∠ABC,把△ABP逆时针旋转,画出旋转后的图形.
拓展延伸题
13.如图23-1-17, △ABD、△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
中考模拟题
14.图形经过平移,旋转,发生改变的特征是( )
A.大小和位置 B.形状和位置
C.形状 D.位置
15.△ABC绕点A按顺时针方向旋转850得△AEF,则以下结论错误的是 ( )
A.∠BAE=850 B.AC=AF
C.EF=BC D.∠EAF=850
16.4张扑克牌如图23-1-18①所示放在桌面上,小敏把其中一张旋转1800后,得到如图23-1-18②所示,那么她所旋转的牌从左数起是 ( )
九年级数学(上)·人教版
23.2中心对称
预习导航学案
[轻松启航]————————————————————————[激活思维]
1.如图23-2-1,线段AC、BD相
交于点O,OA=OC,OB=OD,把
△OCD绕点O旋转1800,则△OCD
与△OAB .
2.把一个图形绕着某一个点旋转1800后,如果它能够与另一个图形重合,那么就说这两个图形关于这个点 或 ,这个点叫做 ,这两个图形中的对应点叫做 .
3.关于中心对称的两个图形,对称点所连线段都经过 ,而且 .
4.关于中心对称的两个图形是 .
5.把一个图形绕某一个点旋转1800,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做 ,这个点是 .
6.线段绕它的中点旋转1800后,它的两个端点互换了位置,旋转后的线段和 重合,因此,线段是 , 是它的对称中心.
7.两个点关于原点对称时,它们的坐标 相反,即点关于原点的对称点为 .
1.□ABCD中,点O 是对角线的交点,因为OA=OC,OB=OD,所以图形绕点O旋转 后,点A与点C,点B与点D分别互换了位置,旋转后的图形和原来的图形重合,因此平行四边形是 ,
是它的对称中心.
2.等边三角形是中心对称图形吗?为什么?
3.已知点A(a,1)与点A′(5,b)关于原点O的对称点,那么a、b是多少?
互动研学教练
[教材研学]————————————————————————[举例说法]
一、中心对称和中心对称图形的区别与联系
中心对称和中心对称图形是两个不同而又紧密联系的概念.
1.区别:中心对称是指两个全等图形之间的相互位置关系,这两个图形关于一点对称,这个点是对称中心,两个图形关于一点对称也叫中心对称.成中心对称的两个图形中,其中一个图形上所有点关于对称中心的对称点都在另一个图形上,反之,另一个图形上所有点的对称点,又都在这个图形上;而中心对称图形是指图形本身成中心对称,中心对称图形上所有点关于对称中心的对称点都在这个图形本身上.
2.联系:如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形;一个
[例1]如图23-2-2, □ABCD的对角线相交于O,E、F在直线BD上,且BE=DF,
说出图中:
(1)四边形AECF是不
是中心对称图形,说出理由.
(2)四边形AECF的对
称中心是什么?
解:(1)四边形AECF是中心对称图形.理由是:因为□ABCD对角线互相平分,所以OA=OC,OB=OD.而BE=DF,因此OB+BE=OD+DF,即OE=OF.由对角线互相平分的四边形是平行四边形,因此四边形AECF是平行四边形,故四边形AECF是中心对称图形.
(2)平行四边形AECF的对称中心是对角线交点O.
[例2]如图23-2-3中的扑克牌中,哪些牌的牌面是中心对称图形?
第二十三章 旋转
中心对称图形,如果把对称的部分看成两个图形,那么它们又是关于中心对称.
二、关于原点对称的坐标
两个点关于原点对称时,它们的坐标符号相反,即点P(a,b)关于原点的对称点为
友情提示:两个点关于原点对称的点的坐标特点一定要与两个点关于x轴或y轴对称的点的坐标特点区别开,两个点关于x轴对称时,它们的横坐标相同,纵坐标符号相反;两个点关于y轴对称时,它们的横坐标符号相反,纵坐标相同,即点P(a,b)关于x轴对称的点P1(a,-b),关于y轴对称的点P2(-a,b).
解:①②为中心对称图形.
点拨:考查中心对称图形,要注意区分每张扑
克牌中的小图案的方向,培养学生严谨的学习态度.
[例3]已知
解:由题意,得
点拨:根据关于原点对称的点的坐标特点,它
们的坐标符号相反,可得
解得a=-,b=4
中考真题在线
[例1] 下列图形中,不是中心对称的是 ( )
A.圆 B.菱形 C.矩形 D.等边三角形
答案:D
点拨:根据中心对称的定义,绕某个点旋转 1800后,旋转后的图形能够重合,故根据定义, 知不是中心对称的是D.
[例2]等边三角形、正方形、菱形、等腰梯形这四种图形中,是中心对称图形的有 ( )
A.1个 B.2个 C.3个 D.4个
答案:B.
点拨:根据中心对称的定义,知正方形、
菱形是中心对称图形,故应选B.
[例3]如图23-2-4,等腰梯形ABCD中,ABCD,AB=2CD,AC交BD于点O,点E、F分别为AO、BO的中点,则下
列关于点O成中心对称
的一组三角形是( )
A.△ABO与△CDO
B.△AOD与△BOC
C.△COD与△EOF
D.△ACD与△BCD
答案:C
点拨:根据中心对称的定义易得.
同步升级演练
基础巩固题
1.下列几何图形中,是中心对称图形而不是轴对称图形的是 ( )
A.等边三角形 B.矩形
C.平行四边形 D.菱形
2.国旗上的每个五角星 ( )
A.是中心对称图形而不是轴对称图形
B.是轴对称图形而不是中心对称图形
C.既是中心对称图形,又是轴对称图形
D.既不是中心对称图形,又不是轴对称图形
3.在等边三角形、平行四边形、正方形和线段四种图形中,既是轴对称图形,又是中心对称图形的有 ( )
A.1种 B.2种 C.3种 D.4种
4.在等腰三角形、等边三角形、平行四边形、矩形、正方形和圆六种图形中,是中心对称图形,而不轴对称图形的有 ( )
A.1种 B.2种 C.3种 D.6种
5.四边形ABCD对角线相交于O,且OA=OB=OC=OD,则这个四边形 ( )
A.仅是轴对称图形
B.仅是中心对称图形
C.既不是中心对称图形,又不是轴对称图形
D.既是中心对称图形,又是轴对称图形
6.图23-2-5中,既是中心对称图形,又是轴对称图形的是 ( )
九年级数学(上)·人教版
7. 图23-2-6中,是中心对称图形的是 ( )
8.中心对称图形上,每一对对称点连成的线段都被 平分.
9.平行四边形是 对称图形,矩形、菱形和正方形不仅是 图形,而且也是 图形.
10.过平行四边形对角线的交点任作一条直线与两边相交(或与两边延长线相交),交点到对角线交点的距离 ,这是因为平行四边形是 .
11.将正方形绕对称中心旋转 后,与原来位置重合.
12.如图23-2-7所示,观察图案并回答下列问题:
(1)图案是不是轴对称图形,如果是,图案有几条对称轴?
(2)图案是不是中心对称图形,为什么?找出对称中心.
(3)图案绕中心旋转多少度能和原来的图案重合?
探究提高题
13.仔细观察如图23-2-8,所列26英文字母,将相应的字填入表格中适当的空格内.
对称 中心对称图形 轴对称图形
只有一对称轴 有两条对称轴
英文字母
14.经过矩形的对称中心任作一直线能否将矩形平分为面积相等的两部分?说明理由.
拓展延伸题
15.如图23-2-9甲所示,魔术师把4张扑克牌放在桌上,然后蒙上眼睛,请一位观众上台,把某一张牌旋转1800,魔术师解除蒙具后,看到4张扑克牌如图23-2-9乙所示,他很快确定了哪一张牌被旋转过,请问:魔术师所指的哪一张牌被旋转过了?他是怎么知道的?
16.观察如图23-2-10中的甲、乙两图,回答下列问题:
甲
乙
图23-2-10
(1)它们是不是轴对称图形、中心对称图形?请分别加以说明.
(2)如果是轴对称图形找出对称轴,如果中心对称图形找出对称中心.
第二十三章 旋转
中考模拟题
17.(2006年·北京宣武质检)图形:①线段;②正五角星;③相交两圆(非等圆);④双曲线.其中是轴对称图形而不是中心对称图形的是( )
A.①③④ B.①③
C.②③ D.③④
18.(2006年·南昌测试)图23-2-11中的图案是几种名车标志,其中是中心对称图形的共( )
A.1个 B.2个 C.3个 D.4个
23.3课题学习 图案设计
23.3课题学习 图案设计
预习导航学案
[轻松启航]————————————————————————[激活思维]
1.在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为 ,平移不改变图形的 和 .
2.经过平移,对应点所连的线段 且 ,对应线段 且 ,对应角 .
3.经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了 ,任意一对对应点与旋转中心的连线所成的角都是 ,对应点到旋转中心的距离 .
4.把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线 ,这条直线叫做 ,两个图形关于直线对称也叫做 .
5.关于某条直线对称的两个图形是 .
1.观察图案23-3-1,可以看作由什么“基本图案”经过怎样的变换形成的?
2.如图23-3-2的图案可以看作是以一个怎样的图案为“基本图案”形成的?试用两种以上的方法分析它的形成过程.
互动研学教练
[教材研学]————————————————————————[举例说法]
一、运用平移、旋转、轴对称等知识对生活中见到的一些美丽的图案分析其形成过程
对生活中的图案,运用平移、旋转、轴对称的观点分析其形成过程,关键是在图案中找到“基本图案”,并运用平移、旋转、轴对称的组合进行变化,检验是否形成给出图案.
二、运用平移、旋转、轴对称进行图案设计
[例1]欣赏如图23-3-3的图案,
并分析图案的形成过程.
解:图案是由图形的四分之一,即四
根J形的“基本图案”,绕图形中心向同
一方向旋转900、1800、2700而形成的.
[例2]利用23-3-4所给图形进行图
案设计,并说明设计的含义.
解:如图23-3-5所示.
九年级数学(上)·人教版
运用平移、旋转、轴对称进行图案设计,首先要选择基本图形,然后制定设计思路,再遵照平移、旋转或轴对称的基本操作对基本图形及其组合进行变化,便可得到相应的图案.
点拨:图案设计就是运用变化图形的方法—
—平移、旋转和轴对称对基本图案进行适当的变
形,组成具有一定意义的新图形.
中考真题在线
[例1](2004年·南安)如图23-3-6,△ABC、△ADE均是顶角为420的等腰
三角形,BC、DE分别是底边,
图中的哪两个三角形可以通
过怎样的旋转而相互得到?
解:△ABC与△ADE可以
通过以点A为旋转中心的旋
转变换而相互得到,旋转角度为420.
[例2](2004年·嘉兴)如图23-3-7,过正方形的中心O点和边上一点P随意连一条曲线,将所画的曲线绕O点按同一方向连续旋转三次,每次的旋转角都是900,这样就将正方
形分成了四部分,这四部分之间
有什么关系?
解:这四部分是大小,形状完全
相同的四块图案.
同步升级演练
基础巩固题
1.利用平移分析图23-3-8中“三鸟”商标的图案(不考虑汉字),并设计一个你所喜欢的徽标图案.
2.利用轴对称分析图23-3-9中“钢鹰”商标的图案(不考虑汉字),并设计一个你喜欢的商标图案.
3.利用旋转分析图23-3-10中“三蝶”商标的图案(不考虑汉字),并设计一个你喜欢的商标图案.
探究提高题
4. 利用旋转和轴对称分析图23-3-11中的图案的形成过程.
第二十三章 旋转
5. 利用平移、旋转和轴对称分析图23-3-11中花边图案的形成过程.
拓展延伸题
6.利用角、线段等基本图形,借助旋转、平移或轴对称设计一个图案,并简述你的设计意图.
7.图23-3-13是一个由“树叶”状图形组成的图案,利用平移、轴对称或旋转分析这个图案的形成过程.
中考模拟题
8.(2006年·南京质检)如图23-3-15的图案中,由图23-3-14经过平移得到的是( )
九年级数学(上)·人教版
第二十二章质量评估
(时间:100分钟 满分:120分)
一、选择题(每小题4分,共24分)
1.在图23-2中,是由图23-1
通过平移得到的图形是 ( )
2.△ABC绕A点按顺时针方向旋转850,得△AEF则以下结论错误的是 ( )
A.∠BAE=850 B.AC=AF
C.EF=BC D.∠EAF=850
3.如图23-3所示,O是正六边形ABCDEF的中点,下列图形中可由△OBC
平移得到的是 ( )
A.△OCD
B.△OAB
C.△OAF
D.△OEF
4.(2005年·烟台)4根火柴棒形成如图23-4所示的象形“口”字,平移火柴棒后,原图形能变成的象形汉字是图23-5中的 ( )
5.在综合实践活动课上,
小红准备用两种不同颜色的布
料缝制一个正方形坐垫,坐垫
图案如图23-6所示,应该选
图23-7中的哪一块布料才能
使其与图23-6拼接符合原来
的图案模式 ( )
6.一电动玩具的正面是由
半径为10cm的小圆盘和半径
为20cm的大圆盘依图23-8
方式连接而成的,小圆盘在大
圆盘的圆周上外切,滚动一周
且不发生滑动(大圆盘不动),
回到原来的位置,在这一过程
中,判断虚线所示位置的三个圆内,图23-9所画的头发、眼睛、嘴巴位置正确的是( )
二、填空题:(每小题3分,共27分)
7.图23-10①②③④⑤⑥⑦中, 是由①平移得出的, 是由平移且旋转得出的.
8.如图23-11所示,已知矩形EFMN是由矩形ABCD经过平移而得到的,AB-1,∠EMF=300,则EM= ,∠ACB= ,矩形EFMN的面积= 。
9.如图23-12所示,
把正方形ABCD沿着对角线
AC的方向平移到正方形A′B′
C′D′的位置,它们的重叠部
分的面积是正方形ABCD的
面积的一半,若AC=,则
正方形移动的距离AA′是 .
10.如图23-13所示的
图案可以看作是一个正方形
经过 次旋转得到的,
每次旋转 .
11.皮皮与毛毛玩一种游
戏,他们要将图23-14中的
图(1)和图(2)中的三角形通过水平或竖直平移的方法得到图(3),平移过程中,每次水平或竖直平稳一个格,先拼完的为胜;皮皮选择了图(1),毛毛选择了图(2),那么 将获胜.
第二十三章 旋转
12.如图23-15所示,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有 个不同的四边形.
13.将5cm长的线段MN向右平移3cm得到线段PQ,则PQ的长度等于 cm,将MN绕平面内一点O旋转1000,得到线段EF,则线段EF的长度等于 cm.
14.将面积为12cm2的正方形ABCD,向上平移5cm得到图形FEGH,则图形EFGH是 形,面积等于 cm2.
15.已知=900,将∠ABC绕平面内一点O旋转300,得到∠EFG,则∠EFG的度数为 .
三、解答题(共66分)
16.(12分)(1)如图23-16,(甲),在方格纸中如何通过平移或旋转这两种变换,由图形A得到图形B,再由图形B得到图形C(对于平移变换要求回答出平移的方向和平移的距离,对于旋转变换要求回答出旋转中心、旋转方向和旋转角度);
(20如图23-16(甲),如果点P、点P3的坐标分别为(0,0)、(2,1),写出点P2的坐标;
(3)如图23-16(乙)是某设计师设计图案的一部分,请你运用旋转变换的方法,在方格纸中将图形绕点O顺时针依次旋转900,1800,2700,依次画出旋转后所得到的图形,你会得到一个美丽的图案,但涂阴影时不要涂错了位置,否则不会出现理想的效果,你来试一试吧!
注:方格纸中的小正方形的边长为1个单位长度.
17.(12分)将图23-17方格中的图案作下列变换,请画出相应的图案;
(1)沿y轴正向平移4个单位;
(2)关于y轴轴对称.
18.(8分)经过平移,图23-18的图形上A点移到E点,作出平移后的图形.
19.(10分)在图23-19中,将ABCO绕O点按顺时针方向分别旋转900,1800,2700,并将相应的△OBC部分涂上阴影,观察所得的图案.
九年级数学(上)·人教版
20.(12分)如图23-20所示,A点坐标为(3,3),将△ABC先向下平移4个单位得△A′B′C′,再将△A′B′C′绕点O逆时针旋转1800得△A′′B′′C′′.请你画出△A′B′C′和△A′′B′′C′′,并写出点A′′的坐标.
21.(12分)观察如图23-21所示图案,(1)它是由怎样的“基本图案”经过旋转而形成的?
(2)如果运用旋转和轴对称的组合,它又是由怎样的“基本图案”通过轴对称和旋转而成?
(3)如果仅用轴对称,它又是由怎样的“基本图案”经过几次轴对称而形成?
期中标准评估
期中标准评估
(时间:100分钟 满分:120分)
一、选择题(每小题4分,共24分)
1.下列各式正确的是 ( )
A.()2=-3 B. =3
C. =-3 D. (-)2=3
2.计算(-)2007·( + )2006的结果为 ( )
A.- B. +
C.-1 D.--
3.计算-(1-)是 ( )
A.3-1 B. 3+1
C.-1 D.+1
4.若1<x<2,则| x-3|+ 的值( )
A.2 x-4 B.-2
C.4-2 x D.2
5.已知3是关于x的方程x2-2a+1=0的一个根,则2 a的值是 ( )
A.11 B.12 C.13 D.14
6.一元二次方程2x2+3x-4=0的根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.不能确定
7.用配方法解关于x的方程x2-px+ q=0,此方程可变形为 ( )
A.( x + )2= B. ( x + )2=
C.( x-)2= D. ( x-)2=
8.一批上衣原价每件240元,经两次降价后每件194.4元,如果每次降价的百分数相同,则每次降价的百分率为 ( )
A.10% B.9% C.8% D.7%
9.如图Z-1所示是一只停泊在平静湖面上的小船,它的“倒影”是图Z-2中的 ( )
10.在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,图Z-3中,不能由一个基本图形通过旋转得到的是 ( )
二、填空题:(每小题3分,共27分)
11.方程(m-1) x|m|+1-2x=3是关于x的一元二次方程,则m= .
12.三角形两边长分别为2和4,第三边是方程x2-4x+3=0的解,则这个三角形的周长为 .
13. x2+5x+2=0的解为 .
14.若|x-3|+(x-y+1)2=0,则= .
15.如图Z-4所示,在
△ABC中,∠C=900,AC=2cm,
把这个三角形在平面内绕点所
走过的路线长是 cm.
16.如图Z-5,边长为
3的正方形ABCD绕点C顺
时针旋转300后得到正方形
EFCG,EF交AD于点H,那么
DH的长为 .
17.两个数的差是2,它们的
平方和是52,则这两个数为
.
18.函数y= +的自变量x的取值范围是 .
三、解答题(共74分)
19.(10分)解下列方程:
(1)3x2+5x=2;
(2)4(x+2)2=25(x-2)2.
九年级数学(上)·人教版
20.(6分)已知y=++18,求代数式-的值.
21.(10分)观察下列各式及其验证过程:
2=.
验证:2==
==.
3=.
验证:3==
==.
(1)按照上述两个等式及其验证过程的基本思想,猜想4的变形结果并进行验证.
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
22.(10分)如图Z-6,在Rt△ABC中,∠C=900,BC=4,AC=4,现将△ABC沿CB方向平移到△A′B′C′的位置.
(1)若平移的距离为3,求△ABC与△A′B′C′重叠部分的面积.
(2)若平移的距离为x(0≤x≤4),求△ABC与△A′B′C′重叠部分的面积y,列出y与x的关系式.
23.(8分)某商店如果将进货价为8元的商品按每件10元出售,每天可销售200件,现采用提高售价,减少进货量方法增加利润,已知这种商品每涨价0.5元,其销售量就减少10件,问应将销售价定为多少时,才能使所赚利润达到720元?这种商品的利润可以达到800元吗?为什么
期中标准评估
24.(10分)读下列解题过程:
题目:已知方程x2+3x+1=0的两个根为α、β,求 + 的值.
解:因为△=32-4×1×1=5>0,所以α≠β.(1)由一元二次方程根与系数的关系,得α+β=-3, αβ=1.(2)
所以 + = + = = =-3.(3)
阅读后回答问题:
上面的解题过程是否正确?若不正确,指出错在哪一步,并写出正确的解题过程.
25.如图Z-7(1)所示,已知两全等正方形ABCD与ABCD,正方形ABCD的顶点C与正方形的中心重合,且绕点C旋转.
(1)当正方形ABCD由图Z-7(1)位置旋转至图Z-7(2)位置时,两个正方形重叠部分的面积是否相等?说明理由.
(2)当正方形ABCD旋转至任意位置旋转至图Z-7(3)时,两个正方形重叠部分的面积会怎样变化?说明你的结论.
26.某商店进了一批服装,进货单价为50元,如果按每件60元出售,可销售800件,如果每件提价1元出售,其销量就减少20件,现在要获利12000元,且销售成本不超过24000元,问这种服装销售单价确定多少为宜,这时应进多少服装?
a+1=-(2a+1),
2b-3=―(―b-1).
a+1=-(2a+1),
2b-3=b+1.
PAGE
47
同课章节目录
