人教版高中数学选择性必修第二册5.3.2第2课时 函数的最大(小)值 同步练习(含解析)
文档属性
| 名称 | 人教版高中数学选择性必修第二册5.3.2第2课时 函数的最大(小)值 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 158.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-14 18:14:02 | ||
图片预览




文档简介
第2课时 函数的最大(小)值
基础过关练
题组一 函数最大(小)值的概念及其求解
1.设f(x)是区间[a,b]上的连续函数,且在(a,b)内可导,则下列结论中正确的是( )
A. f(x)的极值点一定是最值点
B. f(x)的最值点一定是极值点
C. f(x)在区间[a,b]上可能没有极值点
D. f(x)在区间[a,b]上可能没有最值点
2.(2020北京清华附中高二下期末)函数f(x)=x·ex的最小值是( )
A.-1
B.-e
C.-
D.不存在
3.(2020浙江杭州六校高二下期中)已知函数f(x)=x3-12x,x∈[-3,3],则f(x)的最大值为( )
A.-9
B.-16
C.16
D.9
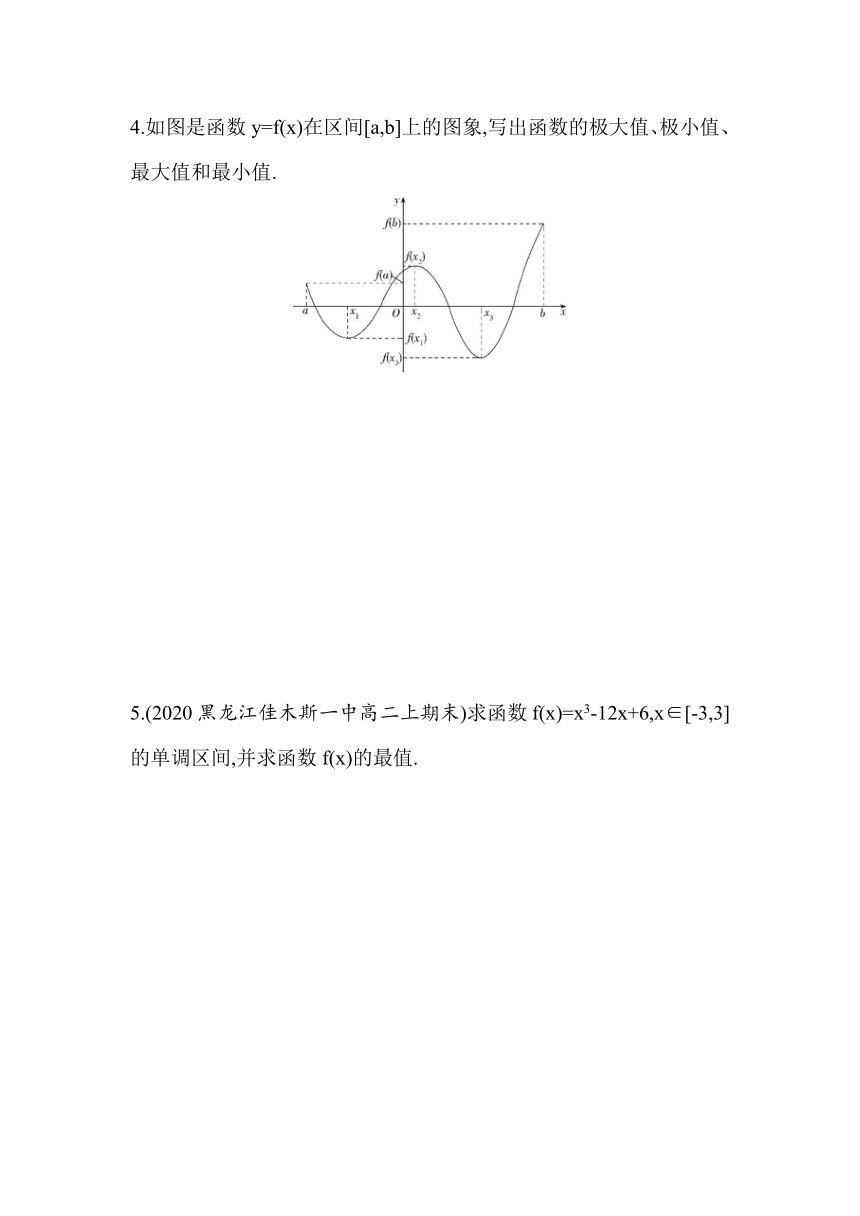
4.如图是函数y=f(x)在区间[a,b]上的图象,写出函数的极大值、极小值、最大值和最小值.
5.(2020黑龙江佳木斯一中高二上期末)求函数f(x)=x3-12x+6,x∈[-3,3]的单调区间,并求函数f(x)的最值.
题组二 含参函数的最大(小)值问题
6.若函数f(x)=asin x+sin 3x在x=处有最大(小)值,则a等于( )
A.2 B.1 C. D.0
7.若函数f(x)=-x3+mx2+1(m≠0)在区间(0,2)上的极大值为最大值,则m的取值范围是 ( )
A.(0,3) B.(-3,0)
C.(-∞,-3) D.(3,+∞)
8.已知函数y=(x>1)有最大值-4,则a的值为( )
A.1 B.-1 C.4 D.-4
9.(2020浙江杭州高二下期中)函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围为 .
10.已知a是实数,函数f(x)=x2(x-a),求f(x)在区间[0,2]上的最大值.
题组三 利用函数的最大(小)值解决不等式问题
11.已知函数f(x)=x2-2ln x,若在定义域内存在x0,使得不等式f(x0)-m≤0成立,则实数m的最小值是( )
A.2 B.-2 C.1 D.-1
12.已知函数f(x)=在区间[1,+∞)上为减函数,则实数a的取值范围为 .
13.设函数f(x)=ln x-x+1.
(1)求函数f(x)的极值;
(2)证明:ln x≤x-1.
14.已知函数f(x)=xln x.
(1)求f(x)的最小值;
(2)若对任意x≥1,都有f(x)≥ax-1,求实数a的取值范围.
题组四 利用导数解决生活中的优化问题
15.某产品的销售收入y1(万元)是产量x(千台)的函数,且函数解析式为y1=17x2(x>0),生产成本y2(万元)是产量x(千台)的函数,且函数解析式为y2=2x3-x2(x>0),要使利润最大,则该产品应生产( )
A.6千台 B.7千台 C.8千台 D.9千台
16.某批发商以每吨20元的价格购进一批建筑材料,若以每吨M元零售,销量N(单位:吨)与零售价M(单位:元)有如下关系:N=8 300-170M-M2,则该批材料零售价定为 元时利润最大,利润的最大值为 元.
17.时下,网校教学越来越受广大学生的喜爱,它已经成为学生课外学习的一种方式.假设某网校的套题每日的销售量y(单位:千套)与销售价格x(单位:元/套)满足关系式:y=+4(x-6)2,其中2(1)求m的值;
(2)假设网校的员工工资、办公费用等所有开销折合为每套题2元(只考虑售出的套题).试确定销售价格x为何值时,网校每日销售套题所获得的利润最大.(保留1位小数)
18.将一块2 m×6 m 的矩形钢板按如图所示的方式划线,要求①至⑦全为矩形,沿线裁去阴影部分,把剩余部分焊接成一个以⑦为底,⑤⑥为盖的水箱,设水箱的高为x m,容积为y m3.
(1)写出y关于x的函数关系式;
(2)当x取何值时,水箱的容积最大
能力提升练
题组一 函数最值问题的求解与应用
1.(2020重庆九校联盟高二上期末联考,)若直线l:x=a与函数f(x)=x2+1,g(x)=ln x的图象分别交于点P、Q,当P、Q两点距离最近时,a=( )
A. B. C.1 D.
2.(2020重庆七校联盟高二上期末联考,)已知函数f(x)的定义域为[-1,5],部分对应值如下表:
x -1 0 4 5
f(x) 1 2 2 1
y=f(x)的导函数y=f'(x)的图象如图所示:
给出下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1其中真命题的个数是( )
A.1 B.2 C.3 D.4
3.()已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调递减区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
题组二 含参函数的最大(小)值问题
4.(2020广东揭阳高二下期末,)若函数f(x)=x3+x2-1在区间(m,m+3)上存在最小值,则实数m的取值范围是( )
A.[-5,0) B.(-5,0)
C.[-3,0) D.(-3,0)
5.(2020湖南长沙长郡中学高二上期末,)已知函数f(x)=(a>0)在[1,+∞)上的最大值为,则a的值为( )
A.-1 B. C. D.+1
6.(2019吉林高二期末,)函数f(x)=ax4-4ax3+b(a>0),x∈[1,4], f(x)的最大值为3,最小值为-6,则ab= .
7.()已知函数f(x)=-2a2ln x+x2+ax(a∈R).
(1)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调区间;
(3)当a<0时,求函数f(x)在区间[1,e]上的最小值.
题组三 利用函数的最大(小)值解决不等式问题
8.()若对任意的x>0,恒有ln x≤px-1(p>0),则p的取值范围是( )
A.(0,1] B.(1,+∞)
C.(0,1) D.[1,+∞)
9.()已知f(x)=ln(x2+1),g(x)=-m,若 x1∈[0,3], x2∈[1,2],使得f(x1)≥g(x2),则实数m的取值范围是( )
A. B.
C. D.
10.(多选)()定义在R上的函数f(x),若存在函数g(x)=ax+b(a,b为常数),使得f(x)≥g(x)对一切实数x都成立,则称g(x)为函数f(x)的一个承托函数,下列命题中正确的是( )
A.函数g(x)=-2是函数f(x)=的一个承托函数
B.函数g(x)=x-1是函数f(x)=x+sin x的一个承托函数
C.若函数g(x)=ax是函数f(x)=ex的一个承托函数,则a的取值范围是[0,e]
D.值域是R的函数f(x)不存在承托函数
11.(2020河北保定高二上期末,)已知函数f(x)=sin x-1,g(x)=ln x-x,若对任意x1∈R都存在x2∈(1,e)使f(x1)12.(2020北京西城高三第一学期期末,)已知函数f(x)=ex-ax+x2,其中a>-1.
(1)当a=0时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)当a=1时,求函数f(x)的单调区间;
(3)若f(x)≥x2+x+b对任意x∈R恒成立,求b-a的最大值.
题组四 利用导数解决生活中的优化问题
13.()某公司生产某种产品,固定成本为20 000元,每生产一单位产品,成本增加100元,已知总营业收入R(元)与年产量x(万吨)的关系是R(x)=则总利润最大时,年产量是( )
A.100万吨 B.150万吨
C.200万吨 D.300万吨
14.()现有一个帐篷,它下部分的形状是高为1 m的正六棱柱,上部分的形状是侧棱长为3 m的正六棱锥(如图所示).当帐篷的体积最大时,帐篷的顶点O到底面中心O1的距离为( )
A.1 m B. m C.2 m D.3 m
15.()某厂生产x件某种产品的总成本为c(x)=(万元),已知产品单价的平方与产品件数x成反比,生产100件这样的产品单价为50万元,则产量定为 件时,总利润最大.
16.(2019山东泰安高三上期中,)如图,AOB是一块半径为r的扇形空地,∠BOG=,∠AOB=.某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.设∠AOD=θ.
(1)记活动场地与停车场占地总面积为f(θ),求f(θ)的表达式;
(2)当cos θ为何值时,可使活动场地与停车场占地总面积最大
答案全解全析
基础过关练
1.C 根据函数的极值与最值的概念知,选项A,B,D都不正确.故选C.
2.C 由题意得, f'(x)=ex+xex=(1+x)ex.
令f'(x)=0,得x=-1.
当x<-1时, f'(x)<0, f(x)单调递减;当x>-1时, f'(x)>0, f(x)单调递增.
因此f(x)在x=-1处取得极小值也是最小值,且最小值为f(-1)=-.故选C.
3.C 由题意得, f'(x)=3x2-12,令f'(x)=0,解得x=±2,易知f(x)在[-3,-2]上单调递增,在[-2,2]上单调递减,在[2,3]上单调递增,又f(-2)=16, f(3)=-9,所以f(x)的最大值为16,故选C.
4.解析 由题图可知y=f(x)在x1,x3处取极小值,在x2处取极大值,所以极小值为f(x1), f(x3),极大值为f(x2);比较极值和端点值可知函数的最小值是f(x3),最大值在b处取得,最大值为f(b).
5.解析 依题意得f'(x)=3x2-12=3(x-2)(x+2), 令f'(x)=0,得x=-2或x=2,列表如下:
x -3 (-3,-2) -2 (-2,2) 2 (2,3) 3
f'(x) + 0 - 0 +
f(x) 15 ↗ 22 ↘ -10 ↗ -3
所以函数f(x)在(-3,-2)和(2,3)上是增函数,在(-2,2)上是减函数,且函数f(x)的最大值是22,最小值是-10.
6.A ∵f(x)在x=处有最大(小)值,
∴x=是函数f(x)的极值点.
又∵f'(x)=acos x+cos 3x(x∈R),
∴f'=acos +cos π=0,解得a=2.
7.A 由题得f'(x)=-3x2+2mx,令f'(x)=0,得x=或x=0(舍去),因为f(x)在区间(0,2)内的极大值为最大值,所以∈(0,2),即0<<2,所以08.B 依题意得y'='===a,令y'=0,解得x=2或x=0(舍去).若函数在区间(1,+∞)上有最大值-4,则最大值必然在x=2处取得,所以=-4,解得a=-1,
此时y'=,
当10,当x>2时,y'<0,可以验证当x=2时y取得最大值-4,故选B.
9.答案 (0,1)
解析 由题意得, f'(x)=3x2-3a,
令f'(x)=0,得x2=a.
∵x∈(0,1),∴要使f(x)在(0,1)内有最小值,只需0<<1,即0当00,可以验证当x=时f(x)取得最小值,故a的取值范围是(0,1).
10.解析 由题意得, f'(x)=3x2-2ax.
令f'(x)=0,得x=0或x=.
①当≤0,即a≤0时, f(x)在[0,2]上单调递增,从而f(x)max=f(2)=8-4a.
②当≥2,即a≥3时, f(x)在[0,2]上单调递减,从而f(x)max=f(0)=0.
③当0<<2,即0综上所述, f(x)max=
11.C 由题可知,函数f(x)的定义域为(0,+∞), f'(x)=2x-.令f'(x)=0,得x=1或x=-1(舍).当x∈(0,1)时, f'(x)<0;当x∈(1,+∞)时, f'(x)>0.所以当x=1时,f(x)取得极小值,也是最小值,且最小值为1.
由题意知m≥1,因此实数m的最小值为1.
12.答案 [e,+∞)
解析 由题意得, f'(x)==.因为f(x)在[1,+∞)上为减函数,所以f'(x)≤0在[1,+∞)上恒成立,即ln a≥1-ln x在[1,+∞)上恒成立,令g(x)=1-ln x,易知函数g(x)=1-ln x在区间[1,+∞)上单调递减,所以g(x)max=g(1)=1,
故ln a≥1,即a≥e.
13.解析 (1)由题意得,函数f(x)的定义域为(0,+∞), f'(x)=-1=,令f'(x)=0,得x=1.
当x变化时, f'(x), f(x)的变化情况如下表:
x (0,1) 1 (1,+∞)
f'(x) + 0 -
f(x) ↗ 极大值 ↘
因此,当x=1时,函数f(x)有极大值,且极大值为f(1)=0.
(2)证明:由(1)可知函数f(x)在x=1处取得最大值,且最大值为0.
即f(x)=ln x-x+1≤0,得 ln x≤x-1.
14.解析 (1)易知f(x)的定义域为(0,+∞),f'(x)=1+ln x.
令f'(x)>0,解得x>,令f'(x)<0,解得0故f(x)的最小值为f=-.
(2)依题意得, f(x)≥ax-1在[1,+∞)上恒成立,即不等式a≤ln x+对任意x∈[1,+∞)恒成立.
令g(x)=ln x+,
则g'(x)=-=.
当x≥1时,g'(x)≥0,故g(x)在[1,+∞)上是增函数,所以g(x)的最小值是g(1)=1,因此a≤g(x)min=g(1)=1,
故a的取值范围为(-∞,1].
15.A 设利润为y万元,则y=y1-y2=17x2-(2x3-x2)=-2x3+18x2(x>0),
∴y'=-6x2+36x=-6x(x-6).
令y'=0,解得x=0(舍去)或x=6,经检验知x=6既是函数的极大值点又是函数的最大值点,∴应生产6千台该产品.
16.答案 30;23 000
解析 设该商品的利润为y元,由题意知,
y=N(M-20)=-M3-150M2+11 700M-166 000,
则y'=-3M2-300M+11 700,
令y'=0,得M=30或M=-130(舍去),
当M∈(0,30)时,y'>0,当M∈(30,+∞)时,y'<0,
因此当M=30时,y取得极大值,也是最大值,且ymax=23 000.
17.解析 (1)由题意知当x=4时,y=21,
代入y=+4(x-6)2,得+16=21,解得m=10.
(2)设每日销售套题所获得的利润为f(x)元.
由(1)可知,套题每日的销售量y=+4(x-6)2,2所以每日销售套题所获得的利润f(x)=(x-2)=10+4(x-6)2(x-2)=4x3-56x2+240x-278(2则f '(x)=12x2-112x+240=4(3x-10)(x-6)(2令f '(x)=0,得x=6(舍去)或x=.
当x∈时,f '(x)>0,函数f(x)单调递增;当x∈时,f '(x)<0,函数f(x)单调递减,
所以x=是函数f(x)在(2,6)内的极大值点,也是最大值点,
所以当x=≈3.3时,函数f(x)取得最大值.
故当销售价格为3.3元/套时,网校每日销售套题所获得的利润最大.
18.解析 (1)由水箱的高为x m,得水箱底面的宽为(2-2x)m,长为=(3-x)m.
故水箱的容积y=(2-2x)(3-x)x
=2x3-8x2+6x(0(2)由(1)得y'=6x2-16x+6,令y'=0,
解得x=(舍去)或x=,
所以y=2x3-8x2+6x(0能力提升练
1.D 由题意知|PQ|=a2+1-ln a.设h(x)=x2+1-ln x(x>0),则h'(x)=2x-=,令h'(x)=0,得4x2-1=0,解得x=(负值舍去).
当x在(0,+∞)上变化时,h'(x)与h(x)的变化情况如下表:
x
h'(x) - 0 +
h(x) ↘ 极小值 ↗
因此,当|PQ|最小时a的值为,故选D.
2.A 由函数f(x)的定义域为[-1,5],知函数y=f(x)不是周期函数,故①错误;由题图知在[0,2]上f'(x)≤0,故f(x)在[0,2]上单调递减,故②正确;依题意可画出函数f(x)的大致图象如图所示:
如果当x∈[-1,t]时, f(x)的最大值是2,那么t的最大值为5,故③错误;当x=2时,f(2)的值不确定,故13.解析 (1)由题意得, f'(x)=-3x2+6x+9.
令f'(x)<0,解得x<-1或x>3,
所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞).
(2)因为f(-2)=8+12-18+a=2+a,
f(2)=-8+12+18+a=22+a,
所以f(2)>f(-2).
因为在(-1,3)上f'(x)>0,
所以f(x)在[-1,2]上单调递增.
又f(x)在[-2,-1]上单调递减,
所以f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,
于是有22+a=20,解得a=-2.
故f(x)=-x3+3x2+9x-2,
因此f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最小值为-7.
4.D 函数f(x)=x3+x2-1的导函数为f'(x)=x2+2x,令f'(x)=0,得x=-2或x=0,
故f(x)在(-∞,-2),(0,+∞)上单调递增,在(-2,0)上单调递减,
则x=0为极小值点,x=-2为极大值点.
由f(x)在区间(m,m+3)上存在最小值,
可得m<0此时f(m)=m3+m2-1=m2(m+3)-1>-1=f(0),因此实数m的取值范围是(-3,0),故选D.
5.A 由f(x)=得, f'(x)=,当a>1时,若x>,则f'(x)<0, f(x)单调递减,若10, f(x)单调递增,故当x=时,函数f(x)有最大值=,得a=<1,不符合题意.当a=1时,函数f(x)在[1,+∞)上单调递减,最大值为f(1)=,不符合题意.当06.答案 1
解析 ∵函数f(x)=ax4-4ax3+b(a>0),x∈[1,4],∴f'(x)=4ax3-12ax2,
令4ax3-12ax2=0,解得x=0或x=3,
f(1)=b-3a, f(3)=b-27a, f(4)=b,且a>0,
∴b-27a∵f(x)的最大值为3,最小值为-6,
∴b=3,b-27a=-6,解得a=,
∴ab=×3=1.
7.解析 (1)函数f(x)的定义域为(0,+∞),当a=1时, f(x)=-2ln x+x2+x,
则f'(x)=-+x+1=,∴f'(1)=0.
又f(1)=,∴曲线y=f(x)在点(1, f(1))处的切线方程为y=.
(2)f'(x)=+x+a=
=(x>0).
若a=0,则f'(x)=x>0, f(x)的单调递增区间为(0,+∞).
若a<0,当x∈(0,-2a)时, f'(x)<0,当x∈(-2a,+∞)时, f'(x)>0,
∴f(x)的单调递减区间为(0,-2a),单调递增区间为(-2a,+∞).
若a>0,当x∈(0,a)时, f'(x)<0,当x∈(a,+∞)时, f'(x)>0,
∴f(x)的单调递减区间为(0,a),单调递增区间为(a,+∞).
(3)由(2)知,当a<0时, f(x)的单调递减区间为(0,-2a),单调递增区间为(-2a,+∞).
当-2a≤1,即-≤a<0时, f(x)在[1,e]上单调递增,则f(x)min=f(1)=+a;
当1<-2a则f(x)min=f(-2a)=-2a2ln(-2a);
当-2a≥e,即a≤-时, f(x)在[1,e]上单调递减,则f(x)min=f(e)=-2a2++ae.
综上,
f(x)min=
8.D 原不等式可化为ln x-px+1≤0,令f(x)=ln x-px+1,则f(x)max≤0.由f'(x)=-p知, f(x)在上单调递增,在上单调递减,故f(x)在x=处取得极大值,也是最大值,故f(x)max=f=-ln p,则有-ln p≤0,解得p≥1.
9.A 由题意得, f'(x)=,易得f(x)在[0,3]上单调递增,所以f(x1)∈[0,ln 10];g'(x)=·ln ,
易得g(x)在[1,2]上单调递减,所以g(x2)∈-m,-m.因为 x1∈[0,3], x2∈[1,2],使得f(x1)≥g(x2),
所以只需0≥-m m≥.故当m≥时,满足题意.
10.BC ∵当x>0时, f(x)=ln x∈(-∞,+∞),∴f(x)≥g(x)=-2对一切实数x不一定都成立,故A错误.
令t(x)=f(x)-g(x),则t(x)=x+sin x-(x-1)=sin x+1≥0恒成立,
∴函数g(x)=x-1是函数f(x)=x+sin x的一个承托函数,故B正确.
令h(x)=ex-ax,则h'(x)=ex-a,
若a=0,由题意知,结论成立.
若a>0,令h'(x)=0,得x=ln a,
∴函数h(x)在(-∞,ln a)上为减函数,在(ln a,+∞)上为增函数,
∴当x=ln a时,函数h(x)取得极小值,也是最小值,为a-aln a,
∵g(x)=ax是函数f(x)=ex的一个承托函数,∴a-aln a≥0,∴ln a≤1,∴0若a<0,当x→-∞时,h(x)→-∞,故不成立.
综上,当0≤a≤e时,函数g(x)=ax是函数f(x)=ex的一个承托函数,故C正确.
不妨令f(x)=2x,g(x)=2x-1,则f(x)-g(x)=1≥0恒成立,
故g(x)=2x-1是f(x)=2x的一个承托函数,故D错误.故选BC.
11.答案 (2e,+∞)
解析 因为对任意x1∈R都存在x2∈(1,e)使f(x1)所以f(x)max又f(x)=sin x-1,所以f(x)max=0,
即存在x∈(1,e),使ln x-x>0,此时ln x>0,
所以a>0,因此问题可转化为存在x∈(1,e),使<成立,
设h(x)=,则对h(x)求导得h'(x)=,
当x∈(1,e)时,h'(x)>0,h(x)单调递增,
所以h(x)2e,
所以实数a的取值范围是(2e,+∞).
解题模板易错警示 分离参数求解不等式恒成立问题的步骤:
12.解析 (1)当a=0时, f(x)=ex+x2,则f'(x)=ex+x, 所以f(0)=1, f'(0)=1.
所以曲线y=f(x)在点(0, f(0))处的切线方程为x-y+1=0.
(2)当a=1时, f(x)=ex-x+x2,
则f'(x)=ex-1+x.
因为f'(0)=0,且f'(x)=ex-1+x在(-∞,+∞)上单调递增,
所以当x>0时, f'(x)>0, f(x)单调递增,当x<0时, f'(x)<0, f(x)单调递减.所以函数f(x)的单调递增区间为(0,+∞),单调递减区间为(-∞,0).
(3)由f(x)≥x2+x+b对任意x∈R恒成立,得ex-(a+1)x-b≥0对任意x∈R恒成立.
设g(x)=ex-(a+1)x-b,则g'(x)=ex-(a+1).
令g'(x)=0,得x=ln(a+1)(a>-1).
当x变化时,g'(x)与g(x)的变化情况如下表所示:
x (-∞,ln(a+1)) ln(a+1) (ln(a+1),+∞)
g'(x) - 0 +
g(x) ↘ 极小值 ↗
所以g(x)在(-∞,ln(a+1))上单调递减,在(ln(a+1),+∞)上单调递增.
所以函数g(x)的最小值为g(ln(a+1))=(a+1)-(a+1)ln(a+1)-b.
由题意,得g(ln(a+1))≥0,即 b-a≤1-(a+1)ln(a+1).
设h(x)=1-xln x(x>0),则h'(x)=-ln x-1.
因为当00;当x>时,-ln x-1<0,
所以h(x)在上单调递增,在,+∞上单调递减.
所以当x=时,h(x)max=h=1+.
所以当a+1=,b=a+1-(a+1)ln(a+1),即a=-1,b=时,b-a有最大值,最大值为1+.
13.D 当年产量为x万吨时,总成本为(20 000+100x)元,总利润为f(x)元,
∴总利润
f(x)=
即f(x)=
所以f'(x)=
①当0≤x≤400时,令f'(x)=0,得x=300,
由f'(x)<0得300由f'(x)>0得0∴当0≤x≤400时,f(x)max=300×300-×3002-20 000=25 000;
②当x>400时,f(x)是减函数,
∴f(x)<60 000-100×400=20 000,
∴当x=300时,f(x)有最大值.故选D.
14.C 设OO1为x m,则1设底面正六边形的面积为S m2,帐篷的体积为V m3.
则由题设可得,正六棱锥底面边长为=(m),
于是S=6×
=(8+2x-x2),
所以V=×(8+2x-x2)(x-1)+×(8+2x-x2)=(8+2x-x2)[(x-1)+3]=(16+12x-x3)(1则V'=(12-3x2).
令V'=0,解得x=2或x=-2(舍去).
当10,V单调递增;
当2所以当x=2时,V最大.故选C.
15.答案 25
解析 设产品的单价为p万元,根据已知,可设p2=,其中k为比例系数.
因为当x=100时,p=50,所以k=250 000,
所以p2=,p=,x>0.
设总利润为y万元,
则y=·x-1 200-x3=500-x3-1 200,
则y'=-x2.令y'=0,得x=25.
故当00;当x>25时,y'<0.
因此当x=25时,函数y取得极大值,也是最大值.
16.解析 (1)由题意得,在矩形OCDE中,∠AOD=θ,∴OC=rcos θ,OE=rsin θ,
∴矩形OCDE的面积为S矩形OCDE=OC·OE=r2sin θcos θ.
又∠BOG=,四边形EFGH是矩形,
∴HG=rsin =,OH=rcos =,
∴HE=OH-OE=r,
∴矩形EFGH的面积为S矩形EFGH=HG·HE=,
∴f(θ)=S矩形OCDE+S矩形EFGH
=r2sin θcos θ+
=r2,θ∈.
(2)由(1)可得, f'(θ)=r2cos2θ-sin2θ-cos θ=·(4cos2θ-cos θ-2),
令f'(θ)=0,得4cos2θ-cos θ-2=0,
解得cos θ=或cos θ=(不合题意,舍去),
令cos θ0=,则θ0∈.
当θ∈(0,θ0)时, f'(θ)>0, f(θ)单调递增;当θ∈时, f'(θ)<0, f(θ)单调递减,
∴当θ=θ0时, f(θ)取得最大值,
即cos θ=时,可使活动场地与停车场占地总面积最大.
基础过关练
题组一 函数最大(小)值的概念及其求解
1.设f(x)是区间[a,b]上的连续函数,且在(a,b)内可导,则下列结论中正确的是( )
A. f(x)的极值点一定是最值点
B. f(x)的最值点一定是极值点
C. f(x)在区间[a,b]上可能没有极值点
D. f(x)在区间[a,b]上可能没有最值点
2.(2020北京清华附中高二下期末)函数f(x)=x·ex的最小值是( )
A.-1
B.-e
C.-
D.不存在
3.(2020浙江杭州六校高二下期中)已知函数f(x)=x3-12x,x∈[-3,3],则f(x)的最大值为( )
A.-9
B.-16
C.16
D.9
4.如图是函数y=f(x)在区间[a,b]上的图象,写出函数的极大值、极小值、最大值和最小值.
5.(2020黑龙江佳木斯一中高二上期末)求函数f(x)=x3-12x+6,x∈[-3,3]的单调区间,并求函数f(x)的最值.
题组二 含参函数的最大(小)值问题
6.若函数f(x)=asin x+sin 3x在x=处有最大(小)值,则a等于( )
A.2 B.1 C. D.0
7.若函数f(x)=-x3+mx2+1(m≠0)在区间(0,2)上的极大值为最大值,则m的取值范围是 ( )
A.(0,3) B.(-3,0)
C.(-∞,-3) D.(3,+∞)
8.已知函数y=(x>1)有最大值-4,则a的值为( )
A.1 B.-1 C.4 D.-4
9.(2020浙江杭州高二下期中)函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围为 .
10.已知a是实数,函数f(x)=x2(x-a),求f(x)在区间[0,2]上的最大值.
题组三 利用函数的最大(小)值解决不等式问题
11.已知函数f(x)=x2-2ln x,若在定义域内存在x0,使得不等式f(x0)-m≤0成立,则实数m的最小值是( )
A.2 B.-2 C.1 D.-1
12.已知函数f(x)=在区间[1,+∞)上为减函数,则实数a的取值范围为 .
13.设函数f(x)=ln x-x+1.
(1)求函数f(x)的极值;
(2)证明:ln x≤x-1.
14.已知函数f(x)=xln x.
(1)求f(x)的最小值;
(2)若对任意x≥1,都有f(x)≥ax-1,求实数a的取值范围.
题组四 利用导数解决生活中的优化问题
15.某产品的销售收入y1(万元)是产量x(千台)的函数,且函数解析式为y1=17x2(x>0),生产成本y2(万元)是产量x(千台)的函数,且函数解析式为y2=2x3-x2(x>0),要使利润最大,则该产品应生产( )
A.6千台 B.7千台 C.8千台 D.9千台
16.某批发商以每吨20元的价格购进一批建筑材料,若以每吨M元零售,销量N(单位:吨)与零售价M(单位:元)有如下关系:N=8 300-170M-M2,则该批材料零售价定为 元时利润最大,利润的最大值为 元.
17.时下,网校教学越来越受广大学生的喜爱,它已经成为学生课外学习的一种方式.假设某网校的套题每日的销售量y(单位:千套)与销售价格x(单位:元/套)满足关系式:y=+4(x-6)2,其中2
(2)假设网校的员工工资、办公费用等所有开销折合为每套题2元(只考虑售出的套题).试确定销售价格x为何值时,网校每日销售套题所获得的利润最大.(保留1位小数)
18.将一块2 m×6 m 的矩形钢板按如图所示的方式划线,要求①至⑦全为矩形,沿线裁去阴影部分,把剩余部分焊接成一个以⑦为底,⑤⑥为盖的水箱,设水箱的高为x m,容积为y m3.
(1)写出y关于x的函数关系式;
(2)当x取何值时,水箱的容积最大
能力提升练
题组一 函数最值问题的求解与应用
1.(2020重庆九校联盟高二上期末联考,)若直线l:x=a与函数f(x)=x2+1,g(x)=ln x的图象分别交于点P、Q,当P、Q两点距离最近时,a=( )
A. B. C.1 D.
2.(2020重庆七校联盟高二上期末联考,)已知函数f(x)的定义域为[-1,5],部分对应值如下表:
x -1 0 4 5
f(x) 1 2 2 1
y=f(x)的导函数y=f'(x)的图象如图所示:
给出下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1
A.1 B.2 C.3 D.4
3.()已知函数f(x)=-x3+3x2+9x+a.
(1)求f(x)的单调递减区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
题组二 含参函数的最大(小)值问题
4.(2020广东揭阳高二下期末,)若函数f(x)=x3+x2-1在区间(m,m+3)上存在最小值,则实数m的取值范围是( )
A.[-5,0) B.(-5,0)
C.[-3,0) D.(-3,0)
5.(2020湖南长沙长郡中学高二上期末,)已知函数f(x)=(a>0)在[1,+∞)上的最大值为,则a的值为( )
A.-1 B. C. D.+1
6.(2019吉林高二期末,)函数f(x)=ax4-4ax3+b(a>0),x∈[1,4], f(x)的最大值为3,最小值为-6,则ab= .
7.()已知函数f(x)=-2a2ln x+x2+ax(a∈R).
(1)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调区间;
(3)当a<0时,求函数f(x)在区间[1,e]上的最小值.
题组三 利用函数的最大(小)值解决不等式问题
8.()若对任意的x>0,恒有ln x≤px-1(p>0),则p的取值范围是( )
A.(0,1] B.(1,+∞)
C.(0,1) D.[1,+∞)
9.()已知f(x)=ln(x2+1),g(x)=-m,若 x1∈[0,3], x2∈[1,2],使得f(x1)≥g(x2),则实数m的取值范围是( )
A. B.
C. D.
10.(多选)()定义在R上的函数f(x),若存在函数g(x)=ax+b(a,b为常数),使得f(x)≥g(x)对一切实数x都成立,则称g(x)为函数f(x)的一个承托函数,下列命题中正确的是( )
A.函数g(x)=-2是函数f(x)=的一个承托函数
B.函数g(x)=x-1是函数f(x)=x+sin x的一个承托函数
C.若函数g(x)=ax是函数f(x)=ex的一个承托函数,则a的取值范围是[0,e]
D.值域是R的函数f(x)不存在承托函数
11.(2020河北保定高二上期末,)已知函数f(x)=sin x-1,g(x)=ln x-x,若对任意x1∈R都存在x2∈(1,e)使f(x1)
(1)当a=0时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)当a=1时,求函数f(x)的单调区间;
(3)若f(x)≥x2+x+b对任意x∈R恒成立,求b-a的最大值.
题组四 利用导数解决生活中的优化问题
13.()某公司生产某种产品,固定成本为20 000元,每生产一单位产品,成本增加100元,已知总营业收入R(元)与年产量x(万吨)的关系是R(x)=则总利润最大时,年产量是( )
A.100万吨 B.150万吨
C.200万吨 D.300万吨
14.()现有一个帐篷,它下部分的形状是高为1 m的正六棱柱,上部分的形状是侧棱长为3 m的正六棱锥(如图所示).当帐篷的体积最大时,帐篷的顶点O到底面中心O1的距离为( )
A.1 m B. m C.2 m D.3 m
15.()某厂生产x件某种产品的总成本为c(x)=(万元),已知产品单价的平方与产品件数x成反比,生产100件这样的产品单价为50万元,则产量定为 件时,总利润最大.
16.(2019山东泰安高三上期中,)如图,AOB是一块半径为r的扇形空地,∠BOG=,∠AOB=.某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.设∠AOD=θ.
(1)记活动场地与停车场占地总面积为f(θ),求f(θ)的表达式;
(2)当cos θ为何值时,可使活动场地与停车场占地总面积最大
答案全解全析
基础过关练
1.C 根据函数的极值与最值的概念知,选项A,B,D都不正确.故选C.
2.C 由题意得, f'(x)=ex+xex=(1+x)ex.
令f'(x)=0,得x=-1.
当x<-1时, f'(x)<0, f(x)单调递减;当x>-1时, f'(x)>0, f(x)单调递增.
因此f(x)在x=-1处取得极小值也是最小值,且最小值为f(-1)=-.故选C.
3.C 由题意得, f'(x)=3x2-12,令f'(x)=0,解得x=±2,易知f(x)在[-3,-2]上单调递增,在[-2,2]上单调递减,在[2,3]上单调递增,又f(-2)=16, f(3)=-9,所以f(x)的最大值为16,故选C.
4.解析 由题图可知y=f(x)在x1,x3处取极小值,在x2处取极大值,所以极小值为f(x1), f(x3),极大值为f(x2);比较极值和端点值可知函数的最小值是f(x3),最大值在b处取得,最大值为f(b).
5.解析 依题意得f'(x)=3x2-12=3(x-2)(x+2), 令f'(x)=0,得x=-2或x=2,列表如下:
x -3 (-3,-2) -2 (-2,2) 2 (2,3) 3
f'(x) + 0 - 0 +
f(x) 15 ↗ 22 ↘ -10 ↗ -3
所以函数f(x)在(-3,-2)和(2,3)上是增函数,在(-2,2)上是减函数,且函数f(x)的最大值是22,最小值是-10.
6.A ∵f(x)在x=处有最大(小)值,
∴x=是函数f(x)的极值点.
又∵f'(x)=acos x+cos 3x(x∈R),
∴f'=acos +cos π=0,解得a=2.
7.A 由题得f'(x)=-3x2+2mx,令f'(x)=0,得x=或x=0(舍去),因为f(x)在区间(0,2)内的极大值为最大值,所以∈(0,2),即0<<2,所以0
此时y'=,
当1
9.答案 (0,1)
解析 由题意得, f'(x)=3x2-3a,
令f'(x)=0,得x2=a.
∵x∈(0,1),∴要使f(x)在(0,1)内有最小值,只需0<<1,即0
10.解析 由题意得, f'(x)=3x2-2ax.
令f'(x)=0,得x=0或x=.
①当≤0,即a≤0时, f(x)在[0,2]上单调递增,从而f(x)max=f(2)=8-4a.
②当≥2,即a≥3时, f(x)在[0,2]上单调递减,从而f(x)max=f(0)=0.
③当0<<2,即0
11.C 由题可知,函数f(x)的定义域为(0,+∞), f'(x)=2x-.令f'(x)=0,得x=1或x=-1(舍).当x∈(0,1)时, f'(x)<0;当x∈(1,+∞)时, f'(x)>0.所以当x=1时,f(x)取得极小值,也是最小值,且最小值为1.
由题意知m≥1,因此实数m的最小值为1.
12.答案 [e,+∞)
解析 由题意得, f'(x)==.因为f(x)在[1,+∞)上为减函数,所以f'(x)≤0在[1,+∞)上恒成立,即ln a≥1-ln x在[1,+∞)上恒成立,令g(x)=1-ln x,易知函数g(x)=1-ln x在区间[1,+∞)上单调递减,所以g(x)max=g(1)=1,
故ln a≥1,即a≥e.
13.解析 (1)由题意得,函数f(x)的定义域为(0,+∞), f'(x)=-1=,令f'(x)=0,得x=1.
当x变化时, f'(x), f(x)的变化情况如下表:
x (0,1) 1 (1,+∞)
f'(x) + 0 -
f(x) ↗ 极大值 ↘
因此,当x=1时,函数f(x)有极大值,且极大值为f(1)=0.
(2)证明:由(1)可知函数f(x)在x=1处取得最大值,且最大值为0.
即f(x)=ln x-x+1≤0,得 ln x≤x-1.
14.解析 (1)易知f(x)的定义域为(0,+∞),f'(x)=1+ln x.
令f'(x)>0,解得x>,令f'(x)<0,解得0
(2)依题意得, f(x)≥ax-1在[1,+∞)上恒成立,即不等式a≤ln x+对任意x∈[1,+∞)恒成立.
令g(x)=ln x+,
则g'(x)=-=.
当x≥1时,g'(x)≥0,故g(x)在[1,+∞)上是增函数,所以g(x)的最小值是g(1)=1,因此a≤g(x)min=g(1)=1,
故a的取值范围为(-∞,1].
15.A 设利润为y万元,则y=y1-y2=17x2-(2x3-x2)=-2x3+18x2(x>0),
∴y'=-6x2+36x=-6x(x-6).
令y'=0,解得x=0(舍去)或x=6,经检验知x=6既是函数的极大值点又是函数的最大值点,∴应生产6千台该产品.
16.答案 30;23 000
解析 设该商品的利润为y元,由题意知,
y=N(M-20)=-M3-150M2+11 700M-166 000,
则y'=-3M2-300M+11 700,
令y'=0,得M=30或M=-130(舍去),
当M∈(0,30)时,y'>0,当M∈(30,+∞)时,y'<0,
因此当M=30时,y取得极大值,也是最大值,且ymax=23 000.
17.解析 (1)由题意知当x=4时,y=21,
代入y=+4(x-6)2,得+16=21,解得m=10.
(2)设每日销售套题所获得的利润为f(x)元.
由(1)可知,套题每日的销售量y=+4(x-6)2,2
当x∈时,f '(x)>0,函数f(x)单调递增;当x∈时,f '(x)<0,函数f(x)单调递减,
所以x=是函数f(x)在(2,6)内的极大值点,也是最大值点,
所以当x=≈3.3时,函数f(x)取得最大值.
故当销售价格为3.3元/套时,网校每日销售套题所获得的利润最大.
18.解析 (1)由水箱的高为x m,得水箱底面的宽为(2-2x)m,长为=(3-x)m.
故水箱的容积y=(2-2x)(3-x)x
=2x3-8x2+6x(0
解得x=(舍去)或x=,
所以y=2x3-8x2+6x(0
1.D 由题意知|PQ|=a2+1-ln a.设h(x)=x2+1-ln x(x>0),则h'(x)=2x-=,令h'(x)=0,得4x2-1=0,解得x=(负值舍去).
当x在(0,+∞)上变化时,h'(x)与h(x)的变化情况如下表:
x
h'(x) - 0 +
h(x) ↘ 极小值 ↗
因此,当|PQ|最小时a的值为,故选D.
2.A 由函数f(x)的定义域为[-1,5],知函数y=f(x)不是周期函数,故①错误;由题图知在[0,2]上f'(x)≤0,故f(x)在[0,2]上单调递减,故②正确;依题意可画出函数f(x)的大致图象如图所示:
如果当x∈[-1,t]时, f(x)的最大值是2,那么t的最大值为5,故③错误;当x=2时,f(2)的值不确定,故1
令f'(x)<0,解得x<-1或x>3,
所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞).
(2)因为f(-2)=8+12-18+a=2+a,
f(2)=-8+12+18+a=22+a,
所以f(2)>f(-2).
因为在(-1,3)上f'(x)>0,
所以f(x)在[-1,2]上单调递增.
又f(x)在[-2,-1]上单调递减,
所以f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,
于是有22+a=20,解得a=-2.
故f(x)=-x3+3x2+9x-2,
因此f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最小值为-7.
4.D 函数f(x)=x3+x2-1的导函数为f'(x)=x2+2x,令f'(x)=0,得x=-2或x=0,
故f(x)在(-∞,-2),(0,+∞)上单调递增,在(-2,0)上单调递减,
则x=0为极小值点,x=-2为极大值点.
由f(x)在区间(m,m+3)上存在最小值,
可得m<0
5.A 由f(x)=得, f'(x)=,当a>1时,若x>,则f'(x)<0, f(x)单调递减,若1
解析 ∵函数f(x)=ax4-4ax3+b(a>0),x∈[1,4],∴f'(x)=4ax3-12ax2,
令4ax3-12ax2=0,解得x=0或x=3,
f(1)=b-3a, f(3)=b-27a, f(4)=b,且a>0,
∴b-27a
∴b=3,b-27a=-6,解得a=,
∴ab=×3=1.
7.解析 (1)函数f(x)的定义域为(0,+∞),当a=1时, f(x)=-2ln x+x2+x,
则f'(x)=-+x+1=,∴f'(1)=0.
又f(1)=,∴曲线y=f(x)在点(1, f(1))处的切线方程为y=.
(2)f'(x)=+x+a=
=(x>0).
若a=0,则f'(x)=x>0, f(x)的单调递增区间为(0,+∞).
若a<0,当x∈(0,-2a)时, f'(x)<0,当x∈(-2a,+∞)时, f'(x)>0,
∴f(x)的单调递减区间为(0,-2a),单调递增区间为(-2a,+∞).
若a>0,当x∈(0,a)时, f'(x)<0,当x∈(a,+∞)时, f'(x)>0,
∴f(x)的单调递减区间为(0,a),单调递增区间为(a,+∞).
(3)由(2)知,当a<0时, f(x)的单调递减区间为(0,-2a),单调递增区间为(-2a,+∞).
当-2a≤1,即-≤a<0时, f(x)在[1,e]上单调递增,则f(x)min=f(1)=+a;
当1<-2a
当-2a≥e,即a≤-时, f(x)在[1,e]上单调递减,则f(x)min=f(e)=-2a2++ae.
综上,
f(x)min=
8.D 原不等式可化为ln x-px+1≤0,令f(x)=ln x-px+1,则f(x)max≤0.由f'(x)=-p知, f(x)在上单调递增,在上单调递减,故f(x)在x=处取得极大值,也是最大值,故f(x)max=f=-ln p,则有-ln p≤0,解得p≥1.
9.A 由题意得, f'(x)=,易得f(x)在[0,3]上单调递增,所以f(x1)∈[0,ln 10];g'(x)=·ln ,
易得g(x)在[1,2]上单调递减,所以g(x2)∈-m,-m.因为 x1∈[0,3], x2∈[1,2],使得f(x1)≥g(x2),
所以只需0≥-m m≥.故当m≥时,满足题意.
10.BC ∵当x>0时, f(x)=ln x∈(-∞,+∞),∴f(x)≥g(x)=-2对一切实数x不一定都成立,故A错误.
令t(x)=f(x)-g(x),则t(x)=x+sin x-(x-1)=sin x+1≥0恒成立,
∴函数g(x)=x-1是函数f(x)=x+sin x的一个承托函数,故B正确.
令h(x)=ex-ax,则h'(x)=ex-a,
若a=0,由题意知,结论成立.
若a>0,令h'(x)=0,得x=ln a,
∴函数h(x)在(-∞,ln a)上为减函数,在(ln a,+∞)上为增函数,
∴当x=ln a时,函数h(x)取得极小值,也是最小值,为a-aln a,
∵g(x)=ax是函数f(x)=ex的一个承托函数,∴a-aln a≥0,∴ln a≤1,∴0
综上,当0≤a≤e时,函数g(x)=ax是函数f(x)=ex的一个承托函数,故C正确.
不妨令f(x)=2x,g(x)=2x-1,则f(x)-g(x)=1≥0恒成立,
故g(x)=2x-1是f(x)=2x的一个承托函数,故D错误.故选BC.
11.答案 (2e,+∞)
解析 因为对任意x1∈R都存在x2∈(1,e)使f(x1)
即存在x∈(1,e),使ln x-x>0,此时ln x>0,
所以a>0,因此问题可转化为存在x∈(1,e),使<成立,
设h(x)=,则
当x∈(1,e)时,h'(x)>0,h(x)单调递增,
所以h(x)
所以实数a的取值范围是(2e,+∞).
解题模板易错警示 分离参数求解不等式恒成立问题的步骤:
12.解析 (1)当a=0时, f(x)=ex+x2,则f'(x)=ex+x, 所以f(0)=1, f'(0)=1.
所以曲线y=f(x)在点(0, f(0))处的切线方程为x-y+1=0.
(2)当a=1时, f(x)=ex-x+x2,
则f'(x)=ex-1+x.
因为f'(0)=0,且f'(x)=ex-1+x在(-∞,+∞)上单调递增,
所以当x>0时, f'(x)>0, f(x)单调递增,当x<0时, f'(x)<0, f(x)单调递减.所以函数f(x)的单调递增区间为(0,+∞),单调递减区间为(-∞,0).
(3)由f(x)≥x2+x+b对任意x∈R恒成立,得ex-(a+1)x-b≥0对任意x∈R恒成立.
设g(x)=ex-(a+1)x-b,则g'(x)=ex-(a+1).
令g'(x)=0,得x=ln(a+1)(a>-1).
当x变化时,g'(x)与g(x)的变化情况如下表所示:
x (-∞,ln(a+1)) ln(a+1) (ln(a+1),+∞)
g'(x) - 0 +
g(x) ↘ 极小值 ↗
所以g(x)在(-∞,ln(a+1))上单调递减,在(ln(a+1),+∞)上单调递增.
所以函数g(x)的最小值为g(ln(a+1))=(a+1)-(a+1)ln(a+1)-b.
由题意,得g(ln(a+1))≥0,即 b-a≤1-(a+1)ln(a+1).
设h(x)=1-xln x(x>0),则h'(x)=-ln x-1.
因为当0
所以h(x)在上单调递增,在,+∞上单调递减.
所以当x=时,h(x)max=h=1+.
所以当a+1=,b=a+1-(a+1)ln(a+1),即a=-1,b=时,b-a有最大值,最大值为1+.
13.D 当年产量为x万吨时,总成本为(20 000+100x)元,总利润为f(x)元,
∴总利润
f(x)=
即f(x)=
所以f'(x)=
①当0≤x≤400时,令f'(x)=0,得x=300,
由f'(x)<0得300
②当x>400时,f(x)是减函数,
∴f(x)<60 000-100×400=20 000,
∴当x=300时,f(x)有最大值.故选D.
14.C 设OO1为x m,则1
则由题设可得,正六棱锥底面边长为=(m),
于是S=6×
=(8+2x-x2),
所以V=×(8+2x-x2)(x-1)+×(8+2x-x2)=(8+2x-x2)[(x-1)+3]=(16+12x-x3)(1
令V'=0,解得x=2或x=-2(舍去).
当1
当2
15.答案 25
解析 设产品的单价为p万元,根据已知,可设p2=,其中k为比例系数.
因为当x=100时,p=50,所以k=250 000,
所以p2=,p=,x>0.
设总利润为y万元,
则y=·x-1 200-x3=500-x3-1 200,
则y'=-x2.令y'=0,得x=25.
故当0
因此当x=25时,函数y取得极大值,也是最大值.
16.解析 (1)由题意得,在矩形OCDE中,∠AOD=θ,∴OC=rcos θ,OE=rsin θ,
∴矩形OCDE的面积为S矩形OCDE=OC·OE=r2sin θcos θ.
又∠BOG=,四边形EFGH是矩形,
∴HG=rsin =,OH=rcos =,
∴HE=OH-OE=r,
∴矩形EFGH的面积为S矩形EFGH=HG·HE=,
∴f(θ)=S矩形OCDE+S矩形EFGH
=r2sin θcos θ+
=r2,θ∈.
(2)由(1)可得, f'(θ)=r2cos2θ-sin2θ-cos θ=·(4cos2θ-cos θ-2),
令f'(θ)=0,得4cos2θ-cos θ-2=0,
解得cos θ=或cos θ=(不合题意,舍去),
令cos θ0=,则θ0∈.
当θ∈(0,θ0)时, f'(θ)>0, f(θ)单调递增;当θ∈时, f'(θ)<0, f(θ)单调递减,
∴当θ=θ0时, f(θ)取得最大值,
即cos θ=时,可使活动场地与停车场占地总面积最大.
