1.1探索勾股定理(第二课时) 课件(24张PPT)
文档属性
| 名称 | 1.1探索勾股定理(第二课时) 课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
新课标 北师大版 八年级上册
2023-2024学年度上学期北师大版精品课件
第一章勾股定理
1.1探索勾股定理(第二课时)
1.会用拼图的方法验证勾股定理,培养探究能力.
2.掌握勾股定理,并能运用勾股定理解决一些实际问题.
学习目标
复习提问
1、勾股定理的内容
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,
探究新知
探究活动一:
请利用边长分别为a,b,c的四个全等直角三角形拼出以斜边c为边长的正方形.
有哪些拼法?
a
b
c
a
b
c
a
b
c
a
b
c
探究新知
拼图展示
图 1
图 2
a
b
c
a
b
c
探究新知
如图1,你能把正方形ABCD的面积表示出来吗?有哪些表示方法?
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
验证方法一:毕达哥拉斯证法
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4× ab
∵ (a+b)2 = c2 + 4× ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
探究新知
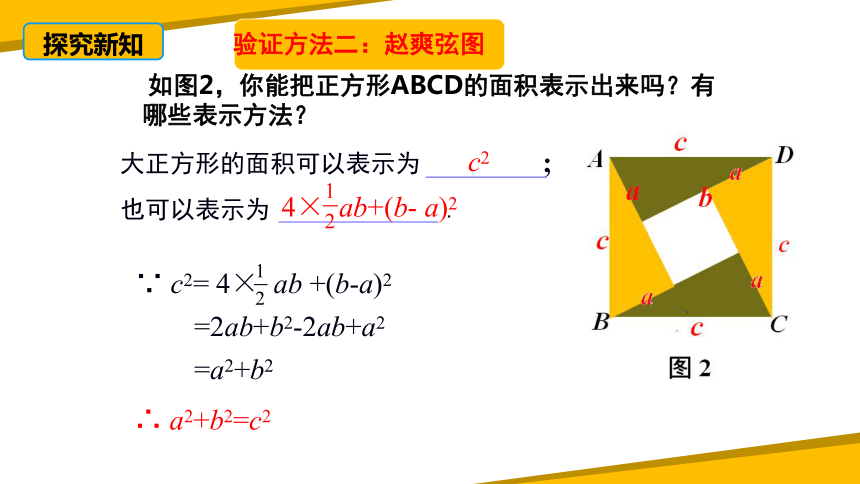
验证方法二:赵爽弦图
大正方形的面积可以表示为 ;
也可以表示为 .
∵ c2= 4× ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴ a2+b2=c2
c2
4× ab+(b- a)2
如图2,你能把正方形ABCD的面积表示出来吗?有哪些表示方法?
例题讲解
例1 我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
解:∵在Rt△ABC中 ∠ACB=90°,
由勾股定理,得AB2=BC2+AC2,
即 5002=BC2+4002,
所以,BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m)
即它行驶的速度为108km/h.
探究新知
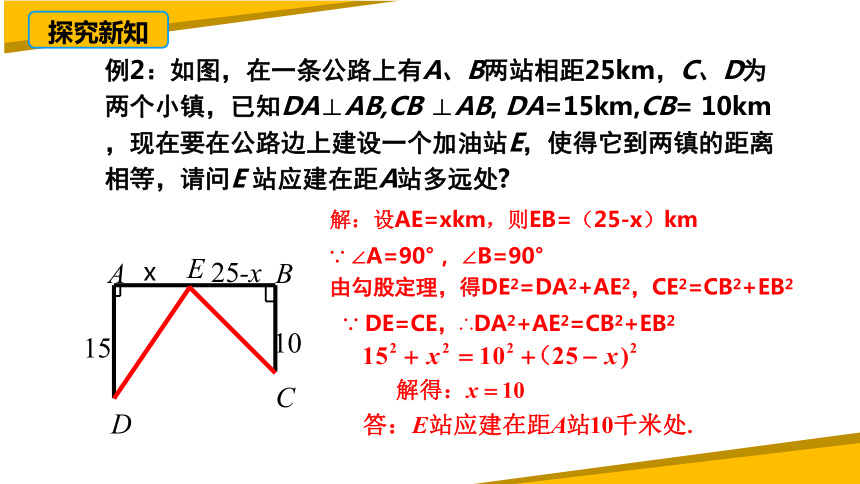
例2:如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E 站应建在距A站多远处
D
A
E
B
C
15
10
25-x
x
解:设AE=xkm,则EB=(25-x)km
∵ ∠A=90°, ∠B=90°
由勾股定理,得DE2=DA2+AE2,CE2=CB2+EB2
∵ DE=CE,∴DA2+AE2=CB2+EB2
探究新知
观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2 。
延伸拓展
A
B
C
A的面积 SA B的面积 SB C的面积
SC
图1
图2
A
B
C
图1
图2
8
9
29
5
8
9
钝角三角形:a2+b2 < c2
锐角三角形:a2+b2 > c2
随堂练习
1.如图是某沿江地区交通图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是100万元/千米,该沿江高速的造价预计是多少?
解:在Rt△MNO中,
根据勾股定理,
∴OM =MN +NO
=300 +400
=5002
∴OM=500 km
同理,得 OQ=1300 km
∴沿江高速长为 OM+OQ=500 +1300=1800 km
∴该沿江高速的造价为 1800× 100=180000 万元
答:该沿江高速的造价预计是180000 万元
随堂练习
2.如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
S梯形ABCD
S梯形ABCD
b
c
a
b
c
a
A
B
C
D
验证方法三:美国总统证法
随堂练习
3.如图,高速公路的同侧有A,B两个村庄,它们到高速公路所在直线MN的距离分别为AA1=2km,BB1=4km,A1B1=8km.现要在高速公路上A1、B1之间设一个出口P,使A,B两个村庄到P的距离之和最短,求这个最短距离和.
随堂练习
解:作点B关于MN的对称
点B′,连接AB′,交A1B1于
P点,连BP.
则AP+BP=AP+PB′=AB′,
易知P点即为到点A,B距离之和最短的点.
过点A作AE⊥BB′于点E,
则AE=A1B1=8km,B′E=AA1+BB1=2+4=6(km).
由勾股定理,得B′A2=AE2+B′E2=82+62,
∴AB′=10(km).即AP+BP=AB′=10km,
故出口P到A,B两村庄的最短距离和是10km.
中考链接
中考链接
课堂小结
探索勾股定理
验证
勾股定理
勾股定理应用
验证方法二:赵爽弦图
验证方法一:毕达哥拉斯证法
验证方法三:美国总统证法
当堂测试
当堂测试
分层作业
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 北师大版 八年级上册
2023-2024学年度上学期北师大版精品课件
第一章勾股定理
1.1探索勾股定理(第二课时)
1.会用拼图的方法验证勾股定理,培养探究能力.
2.掌握勾股定理,并能运用勾股定理解决一些实际问题.
学习目标
复习提问
1、勾股定理的内容
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,
探究新知
探究活动一:
请利用边长分别为a,b,c的四个全等直角三角形拼出以斜边c为边长的正方形.
有哪些拼法?
a
b
c
a
b
c
a
b
c
a
b
c
探究新知
拼图展示
图 1
图 2
a
b
c
a
b
c
探究新知
如图1,你能把正方形ABCD的面积表示出来吗?有哪些表示方法?
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
验证方法一:毕达哥拉斯证法
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4× ab
∵ (a+b)2 = c2 + 4× ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
探究新知
验证方法二:赵爽弦图
大正方形的面积可以表示为 ;
也可以表示为 .
∵ c2= 4× ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴ a2+b2=c2
c2
4× ab+(b- a)2
如图2,你能把正方形ABCD的面积表示出来吗?有哪些表示方法?
例题讲解
例1 我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
解:∵在Rt△ABC中 ∠ACB=90°,
由勾股定理,得AB2=BC2+AC2,
即 5002=BC2+4002,
所以,BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m)
即它行驶的速度为108km/h.
探究新知
例2:如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E 站应建在距A站多远处
D
A
E
B
C
15
10
25-x
x
解:设AE=xkm,则EB=(25-x)km
∵ ∠A=90°, ∠B=90°
由勾股定理,得DE2=DA2+AE2,CE2=CB2+EB2
∵ DE=CE,∴DA2+AE2=CB2+EB2
探究新知
观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2 。
延伸拓展
A
B
C
A的面积 SA B的面积 SB C的面积
SC
图1
图2
A
B
C
图1
图2
8
9
29
5
8
9
钝角三角形:a2+b2 < c2
锐角三角形:a2+b2 > c2
随堂练习
1.如图是某沿江地区交通图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是100万元/千米,该沿江高速的造价预计是多少?
解:在Rt△MNO中,
根据勾股定理,
∴OM =MN +NO
=300 +400
=5002
∴OM=500 km
同理,得 OQ=1300 km
∴沿江高速长为 OM+OQ=500 +1300=1800 km
∴该沿江高速的造价为 1800× 100=180000 万元
答:该沿江高速的造价预计是180000 万元
随堂练习
2.如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
S梯形ABCD
S梯形ABCD
b
c
a
b
c
a
A
B
C
D
验证方法三:美国总统证法
随堂练习
3.如图,高速公路的同侧有A,B两个村庄,它们到高速公路所在直线MN的距离分别为AA1=2km,BB1=4km,A1B1=8km.现要在高速公路上A1、B1之间设一个出口P,使A,B两个村庄到P的距离之和最短,求这个最短距离和.
随堂练习
解:作点B关于MN的对称
点B′,连接AB′,交A1B1于
P点,连BP.
则AP+BP=AP+PB′=AB′,
易知P点即为到点A,B距离之和最短的点.
过点A作AE⊥BB′于点E,
则AE=A1B1=8km,B′E=AA1+BB1=2+4=6(km).
由勾股定理,得B′A2=AE2+B′E2=82+62,
∴AB′=10(km).即AP+BP=AB′=10km,
故出口P到A,B两村庄的最短距离和是10km.
中考链接
中考链接
课堂小结
探索勾股定理
验证
勾股定理
勾股定理应用
验证方法二:赵爽弦图
验证方法一:毕达哥拉斯证法
验证方法三:美国总统证法
当堂测试
当堂测试
分层作业
分层作业
分层作业
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
