12.1函数 同步练习(含答案)沪科版数学八年级上册
文档属性
| 名称 | 12.1函数 同步练习(含答案)沪科版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 312.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 22:30:19 | ||
图片预览


文档简介
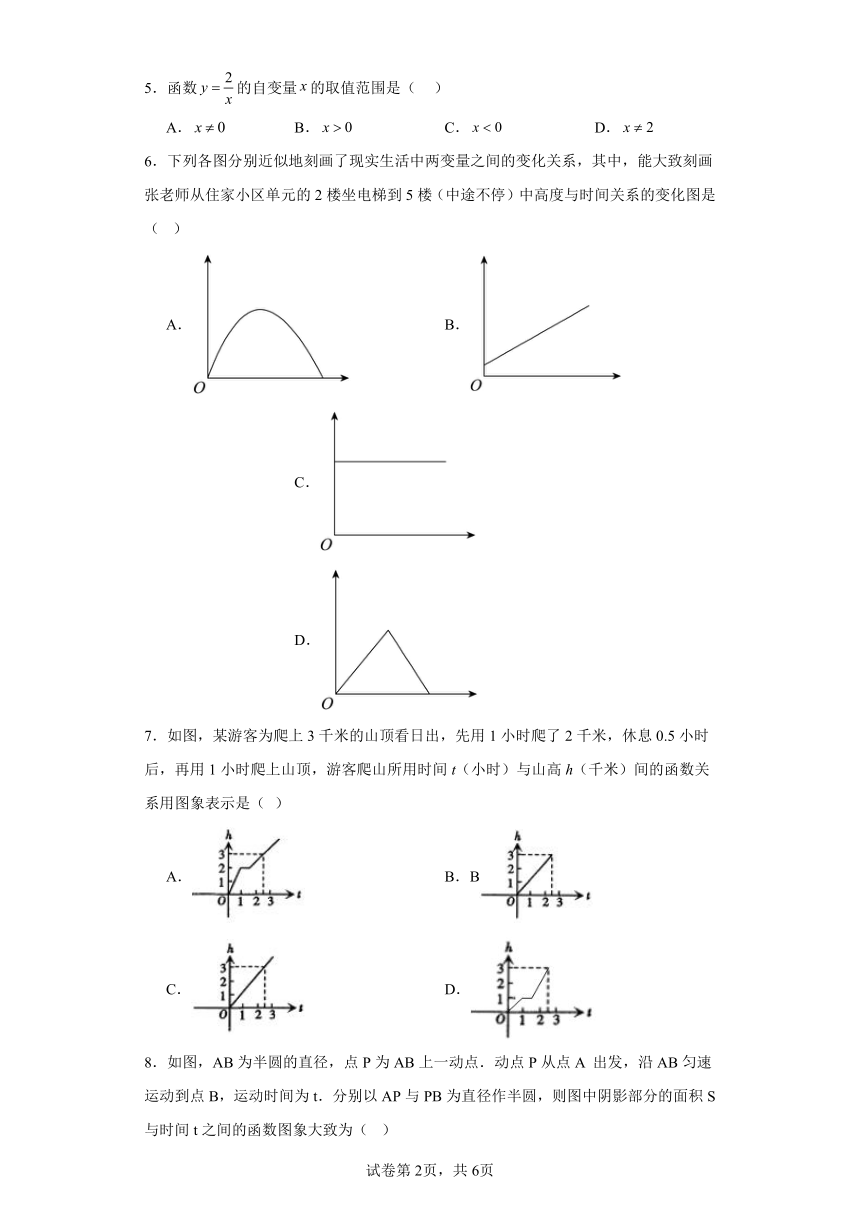
12.1函数同步练习-沪科版数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数中,自变量的取值范围是( )
A. B. C. D.
2.在函数y=中,自变量x的取值范围是( )
A.x≥0 B.x>0 C.x≠0 D.x>0且x≠1
3.甲、乙两车在同一直线公路上匀速行驶,开始时甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设乙车行驶的时间为x秒,两车间的距离为y米,图中折线表示y关于x的函数图象,下列四种说法中正确的有( )
①开始时,两车的距离为500米;②转货用了100秒;
③甲的速度为25米/秒,乙的速度为30米/秒;
④当乙车返回到出发地时,甲车离乙车900米.
A.① B.①② C.②③ D.①②④
4.小明的父亲饭后出去散步,从家中出发走20分钟到一个离家900米的报亭看报10分钟后,用15分钟返回家,下列图中表示小明的父亲离家的距离y(米)与离家的时间x(分)之间的函数关系的是( )
A. B. C. D.
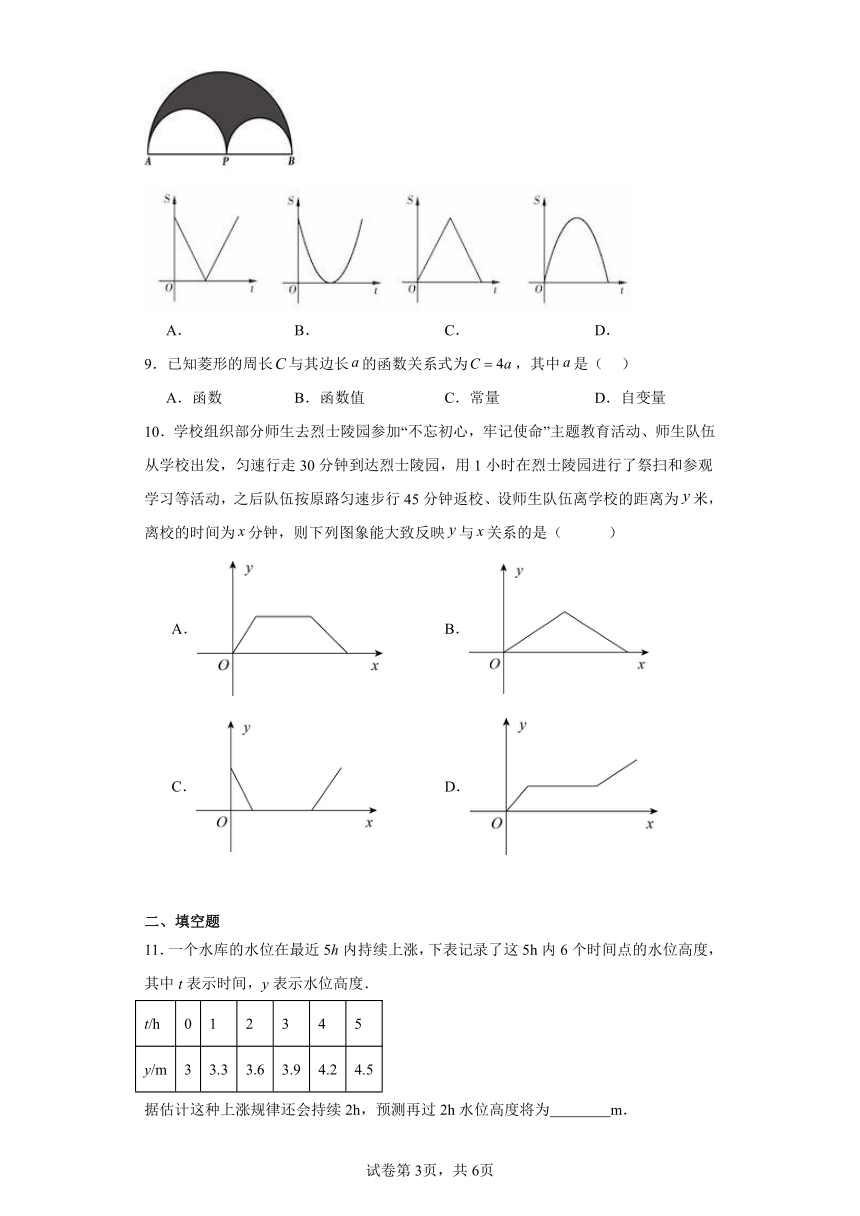
5.函数的自变量的取值范围是( )
A. B. C. D.
6.下列各图分别近似地刻画了现实生活中两变量之间的变化关系,其中,能大致刻画张老师从住家小区单元的2楼坐电梯到5楼(中途不停)中高度与时间关系的变化图是( )
A. B. C. D.
7.如图,某游客为爬上3千米的山顶看日出,先用1小时爬了2千米,休息0.5小时后,再用1小时爬上山顶,游客爬山所用时间t(小时)与山高h(千米)间的函数关系用图象表示是( )
A. B.B
C. D.
8.如图,AB为半圆的直径,点P为AB上一动点.动点P从点A 出发,沿AB匀速运动到点B,运动时间为t.分别以AP与PB为直径作半圆,则图中阴影部分的面积S与时间t之间的函数图象大致为( )
A. B. C. D.
9.已知菱形的周长与其边长的函数关系式为,其中是( )
A.函数 B.函数值 C.常量 D.自变量
10.学校组织部分师生去烈士陵园参加“不忘初心,牢记使命”主题教育活动、师生队伍从学校出发,匀速行走30分钟到达烈士陵园,用1小时在烈士陵园进行了祭扫和参观学习等活动,之后队伍按原路匀速步行45分钟返校、设师生队伍离学校的距离为米,离校的时间为分钟,则下列图象能大致反映与关系的是( )
A. B.
C. D.
二、填空题
11.一个水库的水位在最近5h内持续上涨,下表记录了这5h内6个时间点的水位高度,其中t表示时间,y表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
据估计这种上涨规律还会持续2h,预测再过2h水位高度将为 m.
12.若函数的函数值,则自变量的值为 .
13.AB两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离S(km)与时间t(h)的关系如图所示,则甲出发 小时后与乙相遇.
14.函数中,自变量x的取值范围为 .
15.如果表示一条直线,那么k的取值范围是 .
16.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是 .
17.某工程队承建km的管道铺设,工期天,施工天后剩余管道km,则与的关系式为 .
18.函数y=中,自变量x的取值范围是
19.函数中,自变量的取值范围为 .
20.已知点P(3,m),Q(n,2)都在函数y=x+b的图象上,则m+n= .
三、解答题
21.某电动车厂2017年各月份生产电动车的数量情况如下表:
时间x/月 1 2 3 4 5 6 7 8 9 10 11 12
月产量y/万辆 8 8.5 9 10 11 12 10 9.5 9 10 10 10.5
(1)为什么称电动车的月产量y为因变量 它是谁的因变量
(2)哪个月份电动车的产量最高 哪个月份电动车的产量最低
(3)哪两个月份之间产量相差最大 根据这两个月的产量,电动车厂的厂长应该怎么做
22.为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程 0 100 200 300 400 …
油箱剩余油量 50 42 34 26 18 …
(1)该轿车油箱的容量为_________L,行驶时,油箱剩余油量为________L;
(2)根据上表数据,写出油箱剩余油量与轿车行驶的路程之间的表达式.
23.某影院的观众席的座位按照下表的方式设置
排数(x) 1 2 3 4 …
座位数(y) 50 53 56 59 …
(1)写出第6排对应的座位数;
(2)写出座位数y与排数x之间的关系;
(3)按照上表所示的规律,某一排可能有70个座位吗?说说你的理由.
24.数学综合实践课上,老师提出问题:如图,有一张长为,宽为的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究:
(1)设小正方形的边长为,长方体体积为,根据长方体的体积公式,可以得到与的函数关系式是 ,其中自变量的取值范围是 ;
(2)列出与的几组对应值如下表:
… 1 …
… 1.3 2.2 2.7 3.0 2.8 2.5 1.5 0.9 …
(注:补全表格,保留1位小数点)
(3)结合函数图象回答:当小正方形的边长约为 时,无盖长方体盒子的体积最大,最
大值约为 .
25.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD 和折线 OABC 表示“龟兔赛跑”时的路程与时间关系,请你根据图中给出的信息,解决下列问题:
(1)折线 OABC 表示赛跑过程中_______的路程与时间的关系, 线段 OD 表示赛跑过程中_______的路程与时间的关系, 赛跑的全程是________米.
(2)兔子在起初每分钟跑多少米,乌龟用多少分钟追上了正在睡觉的兔子.
(3)兔子醒来,以 48 千米/小时的速度跑向终点,结果还是比乌龟晚到 0.5 分钟,请你算算兔子中间停下睡觉用了多少分钟?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.B
4.D
5.A
6.B
7.D
8.D
9.D
10.A
11.5.1
12.3或±2
13.2
14..
15.任意实数
16.h=n+6/ h=6+n
17.y=30-0.5x(0≤x≤60)
18.x≥
19.x≥且x≠1
20.5
21.(1)月产量y是时间x的因变量;(2)6月份产量最高,1月份产量最低;(3)6月份和1月份相差最大,在1月份加紧生产,实现产量的增值
22.(1)50,30;(2)
23.(1)第6排的座位数为65个
(2)座位数y与排数x之间的关系式为:y=3x+47
(3)某一排座位数不可能70个座位;
24.(1);0﹤﹤(2)3.0;2.0(3)0.55;3.03
25.(1)兔子,乌龟,1500;(2)兔子在起初每分钟跑700米,乌龟用14分钟追上了正在睡觉的兔子;(3)兔子中间停下睡觉用了28.5分钟.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.函数中,自变量的取值范围是( )
A. B. C. D.
2.在函数y=中,自变量x的取值范围是( )
A.x≥0 B.x>0 C.x≠0 D.x>0且x≠1
3.甲、乙两车在同一直线公路上匀速行驶,开始时甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设乙车行驶的时间为x秒,两车间的距离为y米,图中折线表示y关于x的函数图象,下列四种说法中正确的有( )
①开始时,两车的距离为500米;②转货用了100秒;
③甲的速度为25米/秒,乙的速度为30米/秒;
④当乙车返回到出发地时,甲车离乙车900米.
A.① B.①② C.②③ D.①②④
4.小明的父亲饭后出去散步,从家中出发走20分钟到一个离家900米的报亭看报10分钟后,用15分钟返回家,下列图中表示小明的父亲离家的距离y(米)与离家的时间x(分)之间的函数关系的是( )
A. B. C. D.
5.函数的自变量的取值范围是( )
A. B. C. D.
6.下列各图分别近似地刻画了现实生活中两变量之间的变化关系,其中,能大致刻画张老师从住家小区单元的2楼坐电梯到5楼(中途不停)中高度与时间关系的变化图是( )
A. B. C. D.
7.如图,某游客为爬上3千米的山顶看日出,先用1小时爬了2千米,休息0.5小时后,再用1小时爬上山顶,游客爬山所用时间t(小时)与山高h(千米)间的函数关系用图象表示是( )
A. B.B
C. D.
8.如图,AB为半圆的直径,点P为AB上一动点.动点P从点A 出发,沿AB匀速运动到点B,运动时间为t.分别以AP与PB为直径作半圆,则图中阴影部分的面积S与时间t之间的函数图象大致为( )
A. B. C. D.
9.已知菱形的周长与其边长的函数关系式为,其中是( )
A.函数 B.函数值 C.常量 D.自变量
10.学校组织部分师生去烈士陵园参加“不忘初心,牢记使命”主题教育活动、师生队伍从学校出发,匀速行走30分钟到达烈士陵园,用1小时在烈士陵园进行了祭扫和参观学习等活动,之后队伍按原路匀速步行45分钟返校、设师生队伍离学校的距离为米,离校的时间为分钟,则下列图象能大致反映与关系的是( )
A. B.
C. D.
二、填空题
11.一个水库的水位在最近5h内持续上涨,下表记录了这5h内6个时间点的水位高度,其中t表示时间,y表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
据估计这种上涨规律还会持续2h,预测再过2h水位高度将为 m.
12.若函数的函数值,则自变量的值为 .
13.AB两地相距20km,甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离S(km)与时间t(h)的关系如图所示,则甲出发 小时后与乙相遇.
14.函数中,自变量x的取值范围为 .
15.如果表示一条直线,那么k的取值范围是 .
16.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是 .
17.某工程队承建km的管道铺设,工期天,施工天后剩余管道km,则与的关系式为 .
18.函数y=中,自变量x的取值范围是
19.函数中,自变量的取值范围为 .
20.已知点P(3,m),Q(n,2)都在函数y=x+b的图象上,则m+n= .
三、解答题
21.某电动车厂2017年各月份生产电动车的数量情况如下表:
时间x/月 1 2 3 4 5 6 7 8 9 10 11 12
月产量y/万辆 8 8.5 9 10 11 12 10 9.5 9 10 10 10.5
(1)为什么称电动车的月产量y为因变量 它是谁的因变量
(2)哪个月份电动车的产量最高 哪个月份电动车的产量最低
(3)哪两个月份之间产量相差最大 根据这两个月的产量,电动车厂的厂长应该怎么做
22.为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程 0 100 200 300 400 …
油箱剩余油量 50 42 34 26 18 …
(1)该轿车油箱的容量为_________L,行驶时,油箱剩余油量为________L;
(2)根据上表数据,写出油箱剩余油量与轿车行驶的路程之间的表达式.
23.某影院的观众席的座位按照下表的方式设置
排数(x) 1 2 3 4 …
座位数(y) 50 53 56 59 …
(1)写出第6排对应的座位数;
(2)写出座位数y与排数x之间的关系;
(3)按照上表所示的规律,某一排可能有70个座位吗?说说你的理由.
24.数学综合实践课上,老师提出问题:如图,有一张长为,宽为的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究:
(1)设小正方形的边长为,长方体体积为,根据长方体的体积公式,可以得到与的函数关系式是 ,其中自变量的取值范围是 ;
(2)列出与的几组对应值如下表:
… 1 …
… 1.3 2.2 2.7 3.0 2.8 2.5 1.5 0.9 …
(注:补全表格,保留1位小数点)
(3)结合函数图象回答:当小正方形的边长约为 时,无盖长方体盒子的体积最大,最
大值约为 .
25.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD 和折线 OABC 表示“龟兔赛跑”时的路程与时间关系,请你根据图中给出的信息,解决下列问题:
(1)折线 OABC 表示赛跑过程中_______的路程与时间的关系, 线段 OD 表示赛跑过程中_______的路程与时间的关系, 赛跑的全程是________米.
(2)兔子在起初每分钟跑多少米,乌龟用多少分钟追上了正在睡觉的兔子.
(3)兔子醒来,以 48 千米/小时的速度跑向终点,结果还是比乌龟晚到 0.5 分钟,请你算算兔子中间停下睡觉用了多少分钟?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.B
4.D
5.A
6.B
7.D
8.D
9.D
10.A
11.5.1
12.3或±2
13.2
14..
15.任意实数
16.h=n+6/ h=6+n
17.y=30-0.5x(0≤x≤60)
18.x≥
19.x≥且x≠1
20.5
21.(1)月产量y是时间x的因变量;(2)6月份产量最高,1月份产量最低;(3)6月份和1月份相差最大,在1月份加紧生产,实现产量的增值
22.(1)50,30;(2)
23.(1)第6排的座位数为65个
(2)座位数y与排数x之间的关系式为:y=3x+47
(3)某一排座位数不可能70个座位;
24.(1);0﹤﹤(2)3.0;2.0(3)0.55;3.03
25.(1)兔子,乌龟,1500;(2)兔子在起初每分钟跑700米,乌龟用14分钟追上了正在睡觉的兔子;(3)兔子中间停下睡觉用了28.5分钟.
答案第1页,共2页
答案第1页,共2页
