2.4 线段、角的轴对称性(第2课时) 课件(31张PPT)
文档属性
| 名称 | 2.4 线段、角的轴对称性(第2课时) 课件(31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
第2章 · 轴对称图形
2.4 线段、角的轴对称性
第2课时 线段垂直平分线的判定
学习目标
1.探索并理解线段垂直平分线是具有特殊性质得点的集合;
2.能运用线段垂直平分线的判定定理解决问题;
3.会用直尺和圆规作已知线段的垂直平分线.
问题情景
如果一个点在一条线段的垂直平分线上,那么这个点到这条线段________的距离相等.
两端
反过来,
如果一个点到一条线段两端的距离相等,那么这个点在这条线段的垂直平分线上吗?
●
●
A
B
探索与思考
操作 在一张薄纸上画一条线段AB.
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
思考1 你能在线段AB上找到一点到线段AB两端距离相等吗?
●
●
A
B
●
O
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
线段AB的中点
思考2 你能在线段AB外找到一点到线段AB两端距离相等吗?
●
●
A
B
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
以线段AB为底边的等腰三角形的顶点
●
P1
思考3 这样的点你能找到多少个?
●
●
A
B
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
●
P1
●
P2
●
P3
●
P3
无数个
这些点有什么特征?
在同一条直线上
猜想:这条直线与线段AB有什么关系?
折一折
这条直线是线段AB的垂直平分线
思考4 怎样证明你的猜测呢?小组合作完成猜想的证明.
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
●
●
A
B
●
P
已知:如图,点P是线段AB外一点,且PA =PB.
求证:点P 在线段AB 的垂直平分线上.
●
O
证明:过点P 作AB 的垂线PO,垂足为点O.
则∠POA =∠POB =90°.
在Rt△POA 和Rt△POB 中,
∴ Rt△POA ≌Rt△POB(HL).
∴ AO =BO.
又 PO⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
你还有其他的证明方法吗?
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
●
●
A
B
●
P
●
O
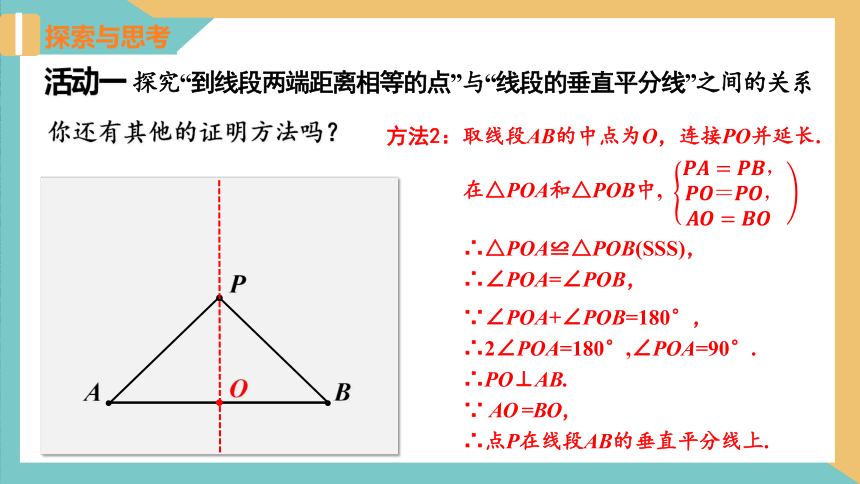
方法2:取线段AB的中点为O,连接PO并延长.
在△POA和△POB中,
∴△POA≌△POB(SSS),
∴∠POA=∠POB,
∵∠POA+∠POB=180°,
∴2∠POA=180°,∠POA=90°.
∴PO⊥AB.
∵ AO =BO,
∴点P在线段AB的垂直平分线上.
你还有其他的证明方法吗?
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
●
●
A
B
●
P
●
O
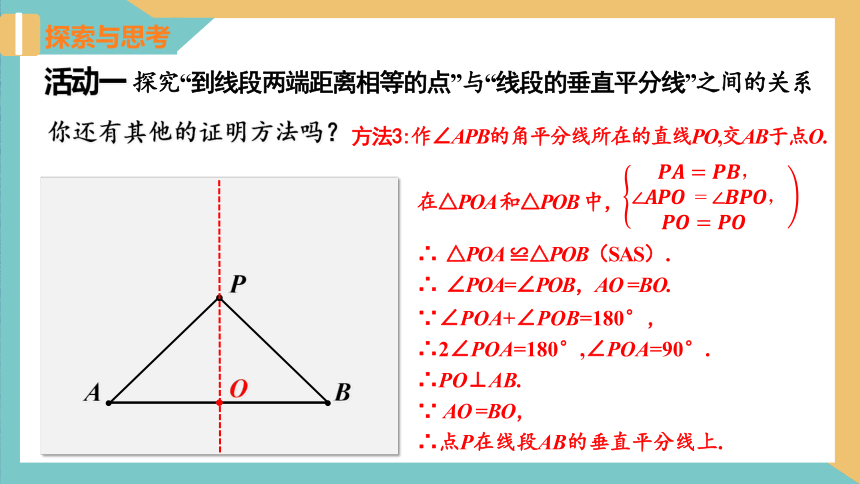
方法3:作∠APB的角平分线所在的直线PO,交AB于点O.
∵∠POA+∠POB=180°,
∴2∠POA=180°,∠POA=90°.
∴PO⊥AB.
∵ AO =BO,
∴点P在线段AB的垂直平分线上.
∴ △POA ≌△POB(SAS).
∴ ∠POA=∠POB,AO =BO.
在△POA 和△POB 中,
到线段两端距离相等的点,在线段的垂直平分线上.
新知归纳
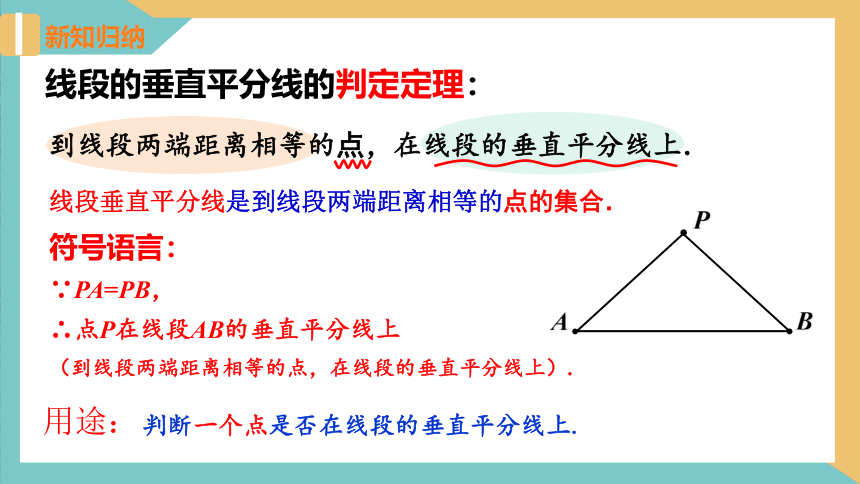
线段的垂直平分线的判定定理:
∵PA=PB,
∴点P在线段AB的垂直平分线上
(到线段两端距离相等的点,在线段的垂直平分线上).
符号语言:
●
●
A
B
●
P
用途:
判断一个点是否在线段的垂直平分线上.
线段垂直平分线是到线段两端距离相等的点的集合.
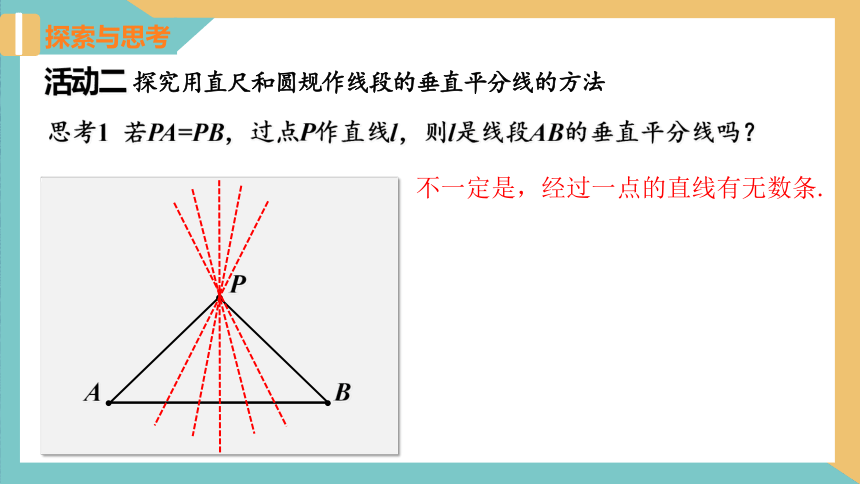
思考1 若PA=PB,过点P作直线l,则l是线段AB的垂直平分线吗?
探索与思考
●
●
A
B
●
P
不一定是,经过一点的直线有无数条.
活动二 探究用直尺和圆规作线段的垂直平分线的方法
思考2 若PA=PB,同时MA=MB,则直线PM是线段AB的垂直平分线吗?
探索与思考
●
●
A
B
●
P
●
M
是,理由:两点确定一条直线.
∵PA =PB,MA =MB,
∴点P、M均在线段AB的垂直平分线上.
根据两点确定一条直线,
∴直线PM垂直平分线段AB.
判定线段垂直平分线的方法
活动二 探究用直尺和圆规作线段的垂直平分线的方法
思考3 你能用尺规画出任一条已知线段的垂直平分线吗?如果能,说说你作图的依据.
探索与思考
●
●
A
B
活动二 探究用直尺和圆规作线段的垂直平分线的方法
作法:
1.分别以点A、B为圆心,大于AB的长为半径画弧,两弧相交于点C、D.
●
C
●
D
2.过C、D两点作直线.
直线CD就是线段AB的垂直平分线.
例题讲解
例 已知:如图,△ABC中,AB、AC的垂直平分线l1、l2相交于点O.
求证:点O在BC的垂直平分线上
B
A
C
O
l1
l2
证明:连接OA、OB、OC.
∵ 点O在AB的垂直平分线上,
∴ OA=OB,
(线段垂直平分线上的点与线段两端距离相等)
同理 OA=OC.
∴ OB=OC.
∴ 点O在BC的垂直平分线上
(与线段两端距离相等的点在这条线段的垂直平分线上) .
新知巩固
1. 已知:如图,点D在BC边上.
(1)若AD=BD,则点D在线段_______的垂直平分线上;
(2)若AC=CD,则点C在线段_______ 的垂直平分线上;
(3)若AB=AC,则点A在线段_______ 的垂直平分线上.
B
A
C
D
AB
AD
BC
新知巩固
2. 如图,四边形ABCD是一个“风筝”骨架,其中AB=AD,CB=CD.
(1)小明认为四边形ABCD的两条对角线AC⊥BD,垂足为E,并且BE=ED,你同意他的说法吗?
解:同意,理由
∵AB=AD,CB=CD,
∴AC是BD的垂直平分线,
∴AC⊥BD,BE=EB.
B
A
D
C
E
新知巩固
(2)设对角线AC=a,BD=b,请用含a、b的式子表示四边形ABCD的面积.
B
A
D
C
E
解:S四边形ABCD=S△CBD+S△ABD
=+
=AC
=b
3. 用直尺和圆规作图:
如图,已知∠AOB和C、D两点,在OB上求作一点P,使PC=PD.
解:连接CD,作CD的垂直平分线与OB相交,交点即为所求.
A
B
O
●
C
●
D
●
P
新知巩固
课堂小结
线段垂直平分线的判定
内容
到线段两端距离相等的点,在线段的垂直平分线上.
用直尺和圆规作已知线段的垂直平分线
作用
判断一个点是否在线段的垂直平分线上.
当堂检测
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.以上都不正确
C
B
D
A
A
当堂检测
2.已知线段AB,在平面上找到三个点D、E、F,使DA=DB,EA=EB,FA=FB,这样的点的组合共有( )种.
A. 1 B. 2 C. 3 D. 无数
D
3. 已知△ABC的三边的垂直平分线交点在△ABC的边上,则△ABC的形状为( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
B
当堂检测
4. 如图,点D在△ABC的边BC上,且BC=BD+DA,则点D在线段( )的垂直平分线上.
A. AB B. AC C. BC D.不能确定
B
B
A
C
D
当堂检测
5.如图,在△ABC中,∠B=70°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为_________.
50°
当堂检测
6.如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E.若△ABC的周长为30,BE=6,则△ABD的周长为______.
18
C
B
A
D
E
当堂检测
证明:∵AD⊥BC,BD=DC,∴AD是BC的垂直平分线,
∴AB=AC.∵AB+BD=DE,
∴AB+BD=DC+CE,∴AC=CE,
∴点C在AE的垂直平分线上.
7. 如图,已知AD⊥BC,BD=DC,AB+BD=DE,
求证:点C在AE的垂直平分线上.
B
A
C
D
E
当堂检测
8. 已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D,连接CD.
求证:OE是CD的垂直平分线.
证明:
∵OE平分∠AOB,
∴∠DOE=∠COE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴△OED≌△OEC(AAS).
∴DO=CO,DE=CE.
∵EC⊥OA,ED⊥OB,
∴∠EDO=∠ECO=90°.
B
A
C
D
O
E
9. 某城区规划局为了方便居民的生活,计划在三个住宅小区A、B、C(如图所示)之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?
(1)在图中用尺规作图确定购物商场的位置;(保留作图痕迹)
●
P
解:(1)作△ABC任意两边的垂直平分线,交点即为所求.
B
●
A
●
C
●
当堂检测
●
P
B
●
A
●
C
●
(2)证明:如答图②,连接PA,PB,PC.∵PF,PQ是BC,AB的垂直平分线,∴PB=PC,PB=PA,
∴PA=PB=PC.
(2)证明你所确定的位置到三个住宅小区的距离相等.
当堂检测
当堂检测
10. 如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,△ADE的周长为12 cm.(1)求BC的长;
解:(1)∵l1垂直平分AB,∴DB=DA,
同理可得EA=EC.∴BC=BD+DE+EC
=DA+DE+EA
=12 cm.
B
A
E
D
C
l1
O
l2
当堂检测
(2)分别连接OA,OB,OC,若△OBC的周长为26 cm,求OA的长.
解:(2)∵l1垂直平分AB,
∴OB=OA.同理可得OA=OC,∴OA=OB=OC.又∵△OBC的周长为26 cm,
BC=12 cm,∴OB+OC=26-12=14(cm),∴OB=OC=7 cm,
∴OA=7 cm.
B
A
E
D
C
l1
O
l2
第2章 · 轴对称图形
2.4 线段、角的轴对称性
第2课时 线段垂直平分线的判定
学习目标
1.探索并理解线段垂直平分线是具有特殊性质得点的集合;
2.能运用线段垂直平分线的判定定理解决问题;
3.会用直尺和圆规作已知线段的垂直平分线.
问题情景
如果一个点在一条线段的垂直平分线上,那么这个点到这条线段________的距离相等.
两端
反过来,
如果一个点到一条线段两端的距离相等,那么这个点在这条线段的垂直平分线上吗?
●
●
A
B
探索与思考
操作 在一张薄纸上画一条线段AB.
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
思考1 你能在线段AB上找到一点到线段AB两端距离相等吗?
●
●
A
B
●
O
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
线段AB的中点
思考2 你能在线段AB外找到一点到线段AB两端距离相等吗?
●
●
A
B
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
以线段AB为底边的等腰三角形的顶点
●
P1
思考3 这样的点你能找到多少个?
●
●
A
B
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
●
P1
●
P2
●
P3
●
P3
无数个
这些点有什么特征?
在同一条直线上
猜想:这条直线与线段AB有什么关系?
折一折
这条直线是线段AB的垂直平分线
思考4 怎样证明你的猜测呢?小组合作完成猜想的证明.
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
●
●
A
B
●
P
已知:如图,点P是线段AB外一点,且PA =PB.
求证:点P 在线段AB 的垂直平分线上.
●
O
证明:过点P 作AB 的垂线PO,垂足为点O.
则∠POA =∠POB =90°.
在Rt△POA 和Rt△POB 中,
∴ Rt△POA ≌Rt△POB(HL).
∴ AO =BO.
又 PO⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
你还有其他的证明方法吗?
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
●
●
A
B
●
P
●
O
方法2:取线段AB的中点为O,连接PO并延长.
在△POA和△POB中,
∴△POA≌△POB(SSS),
∴∠POA=∠POB,
∵∠POA+∠POB=180°,
∴2∠POA=180°,∠POA=90°.
∴PO⊥AB.
∵ AO =BO,
∴点P在线段AB的垂直平分线上.
你还有其他的证明方法吗?
探索与思考
活动一 探究“到线段两端距离相等的点”与“线段的垂直平分线”之间的关系
●
●
A
B
●
P
●
O
方法3:作∠APB的角平分线所在的直线PO,交AB于点O.
∵∠POA+∠POB=180°,
∴2∠POA=180°,∠POA=90°.
∴PO⊥AB.
∵ AO =BO,
∴点P在线段AB的垂直平分线上.
∴ △POA ≌△POB(SAS).
∴ ∠POA=∠POB,AO =BO.
在△POA 和△POB 中,
到线段两端距离相等的点,在线段的垂直平分线上.
新知归纳
线段的垂直平分线的判定定理:
∵PA=PB,
∴点P在线段AB的垂直平分线上
(到线段两端距离相等的点,在线段的垂直平分线上).
符号语言:
●
●
A
B
●
P
用途:
判断一个点是否在线段的垂直平分线上.
线段垂直平分线是到线段两端距离相等的点的集合.
思考1 若PA=PB,过点P作直线l,则l是线段AB的垂直平分线吗?
探索与思考
●
●
A
B
●
P
不一定是,经过一点的直线有无数条.
活动二 探究用直尺和圆规作线段的垂直平分线的方法
思考2 若PA=PB,同时MA=MB,则直线PM是线段AB的垂直平分线吗?
探索与思考
●
●
A
B
●
P
●
M
是,理由:两点确定一条直线.
∵PA =PB,MA =MB,
∴点P、M均在线段AB的垂直平分线上.
根据两点确定一条直线,
∴直线PM垂直平分线段AB.
判定线段垂直平分线的方法
活动二 探究用直尺和圆规作线段的垂直平分线的方法
思考3 你能用尺规画出任一条已知线段的垂直平分线吗?如果能,说说你作图的依据.
探索与思考
●
●
A
B
活动二 探究用直尺和圆规作线段的垂直平分线的方法
作法:
1.分别以点A、B为圆心,大于AB的长为半径画弧,两弧相交于点C、D.
●
C
●
D
2.过C、D两点作直线.
直线CD就是线段AB的垂直平分线.
例题讲解
例 已知:如图,△ABC中,AB、AC的垂直平分线l1、l2相交于点O.
求证:点O在BC的垂直平分线上
B
A
C
O
l1
l2
证明:连接OA、OB、OC.
∵ 点O在AB的垂直平分线上,
∴ OA=OB,
(线段垂直平分线上的点与线段两端距离相等)
同理 OA=OC.
∴ OB=OC.
∴ 点O在BC的垂直平分线上
(与线段两端距离相等的点在这条线段的垂直平分线上) .
新知巩固
1. 已知:如图,点D在BC边上.
(1)若AD=BD,则点D在线段_______的垂直平分线上;
(2)若AC=CD,则点C在线段_______ 的垂直平分线上;
(3)若AB=AC,则点A在线段_______ 的垂直平分线上.
B
A
C
D
AB
AD
BC
新知巩固
2. 如图,四边形ABCD是一个“风筝”骨架,其中AB=AD,CB=CD.
(1)小明认为四边形ABCD的两条对角线AC⊥BD,垂足为E,并且BE=ED,你同意他的说法吗?
解:同意,理由
∵AB=AD,CB=CD,
∴AC是BD的垂直平分线,
∴AC⊥BD,BE=EB.
B
A
D
C
E
新知巩固
(2)设对角线AC=a,BD=b,请用含a、b的式子表示四边形ABCD的面积.
B
A
D
C
E
解:S四边形ABCD=S△CBD+S△ABD
=+
=AC
=b
3. 用直尺和圆规作图:
如图,已知∠AOB和C、D两点,在OB上求作一点P,使PC=PD.
解:连接CD,作CD的垂直平分线与OB相交,交点即为所求.
A
B
O
●
C
●
D
●
P
新知巩固
课堂小结
线段垂直平分线的判定
内容
到线段两端距离相等的点,在线段的垂直平分线上.
用直尺和圆规作已知线段的垂直平分线
作用
判断一个点是否在线段的垂直平分线上.
当堂检测
1.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.以上都不正确
C
B
D
A
A
当堂检测
2.已知线段AB,在平面上找到三个点D、E、F,使DA=DB,EA=EB,FA=FB,这样的点的组合共有( )种.
A. 1 B. 2 C. 3 D. 无数
D
3. 已知△ABC的三边的垂直平分线交点在△ABC的边上,则△ABC的形状为( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
B
当堂检测
4. 如图,点D在△ABC的边BC上,且BC=BD+DA,则点D在线段( )的垂直平分线上.
A. AB B. AC C. BC D.不能确定
B
B
A
C
D
当堂检测
5.如图,在△ABC中,∠B=70°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为_________.
50°
当堂检测
6.如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E.若△ABC的周长为30,BE=6,则△ABD的周长为______.
18
C
B
A
D
E
当堂检测
证明:∵AD⊥BC,BD=DC,∴AD是BC的垂直平分线,
∴AB=AC.∵AB+BD=DE,
∴AB+BD=DC+CE,∴AC=CE,
∴点C在AE的垂直平分线上.
7. 如图,已知AD⊥BC,BD=DC,AB+BD=DE,
求证:点C在AE的垂直平分线上.
B
A
C
D
E
当堂检测
8. 已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D,连接CD.
求证:OE是CD的垂直平分线.
证明:
∵OE平分∠AOB,
∴∠DOE=∠COE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴△OED≌△OEC(AAS).
∴DO=CO,DE=CE.
∵EC⊥OA,ED⊥OB,
∴∠EDO=∠ECO=90°.
B
A
C
D
O
E
9. 某城区规划局为了方便居民的生活,计划在三个住宅小区A、B、C(如图所示)之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场距离相等?
(1)在图中用尺规作图确定购物商场的位置;(保留作图痕迹)
●
P
解:(1)作△ABC任意两边的垂直平分线,交点即为所求.
B
●
A
●
C
●
当堂检测
●
P
B
●
A
●
C
●
(2)证明:如答图②,连接PA,PB,PC.∵PF,PQ是BC,AB的垂直平分线,∴PB=PC,PB=PA,
∴PA=PB=PC.
(2)证明你所确定的位置到三个住宅小区的距离相等.
当堂检测
当堂检测
10. 如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,△ADE的周长为12 cm.(1)求BC的长;
解:(1)∵l1垂直平分AB,∴DB=DA,
同理可得EA=EC.∴BC=BD+DE+EC
=DA+DE+EA
=12 cm.
B
A
E
D
C
l1
O
l2
当堂检测
(2)分别连接OA,OB,OC,若△OBC的周长为26 cm,求OA的长.
解:(2)∵l1垂直平分AB,
∴OB=OA.同理可得OA=OC,∴OA=OB=OC.又∵△OBC的周长为26 cm,
BC=12 cm,∴OB+OC=26-12=14(cm),∴OB=OC=7 cm,
∴OA=7 cm.
B
A
E
D
C
l1
O
l2
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
