第4章 几何图形初步 单元复习课件(54张PPT)
文档属性
| 名称 | 第4章 几何图形初步 单元复习课件(54张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 13:57:55 | ||
图片预览


文档简介
(共54张PPT)
单元小结
第四单元
第4章 几何图形初步
01
03
04
02
05
举一反三
知识梳理
易错考点
高频考点
章节框图
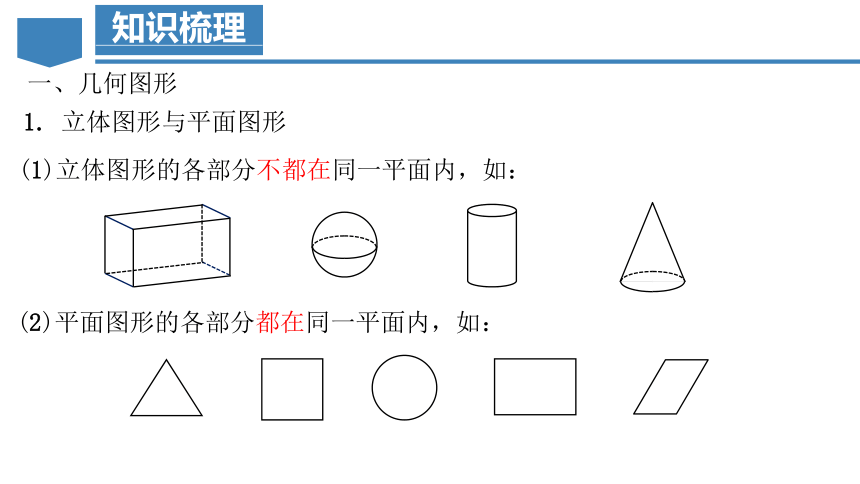
一、几何图形
1. 立体图形与平面图形
(1)立体图形的各部分不都在同一平面内,如:
(2)平面图形的各部分都在同一平面内,如:
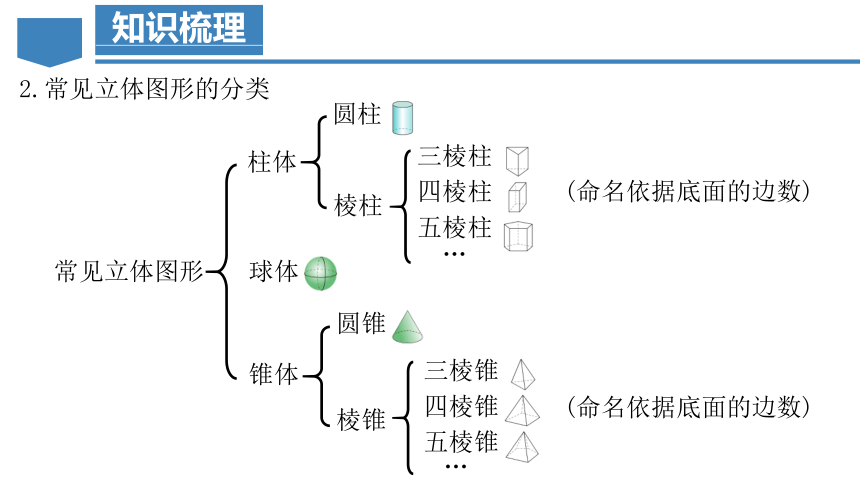
常见立体图形
柱体
锥体
球体
圆柱
棱柱
三棱柱
四棱柱
五棱柱
…
圆锥
棱锥
三棱锥
四棱锥
五棱锥
…
2.常见立体图形的分类
(命名依据底面的边数)
(命名依据底面的边数)
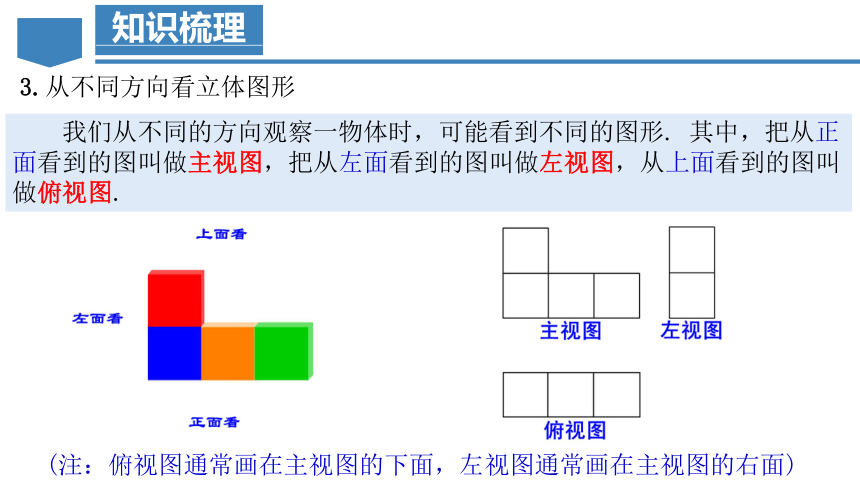
我们从不同的方向观察一物体时,可能看到不同的图形. 其中,把从正面看到的图叫做主视图,把从左面看到的图叫做左视图,从上面看到的图叫做俯视图.
(注:俯视图通常画在主视图的下面,左视图通常画在主视图的右面)
3.从不同方向看立体图形
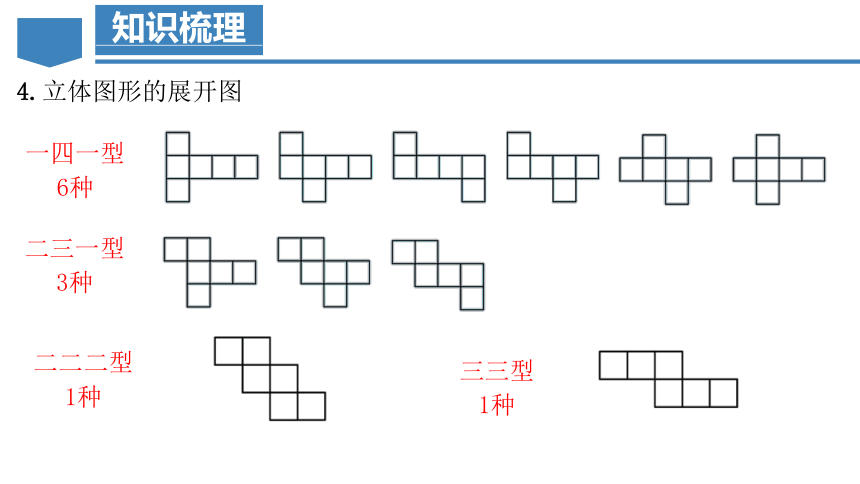
一四一型
6种
二三一型
3种
二二二型
1种
三三型
1种
4.立体图形的展开图
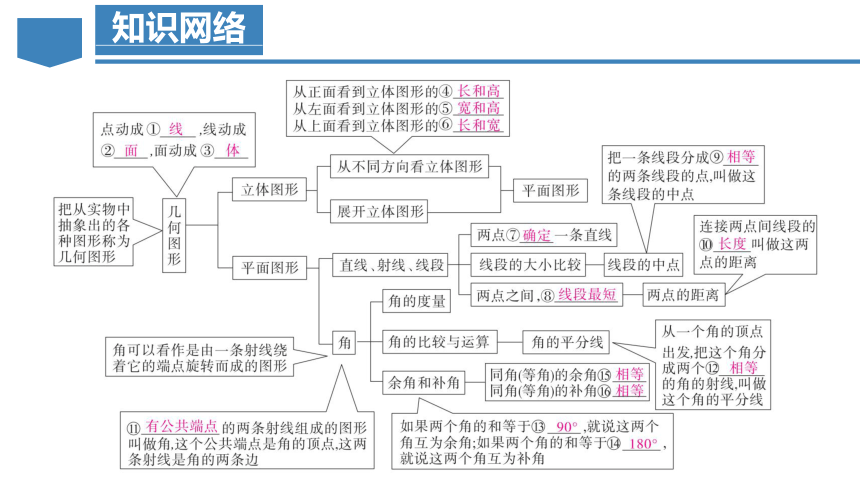
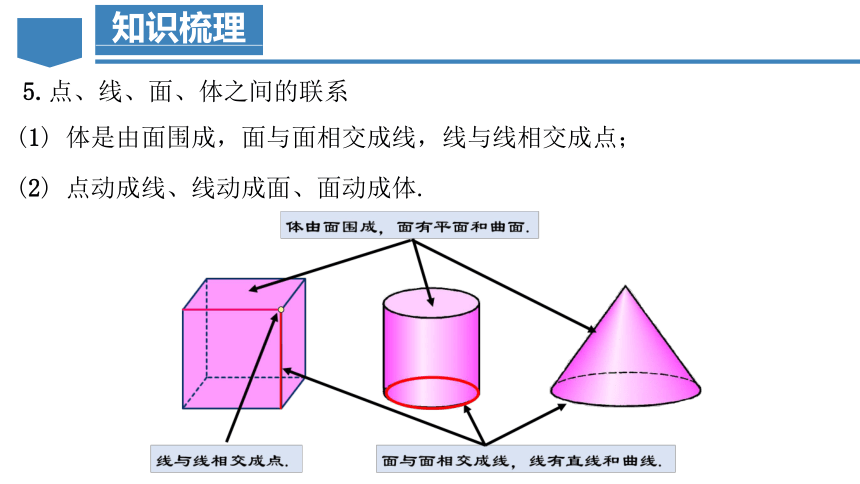
5.点、线、面、体之间的联系
(1) 体是由面围成,面与面相交成线,线与线相交成点;
(2) 点动成线、线动成面、面动成体.
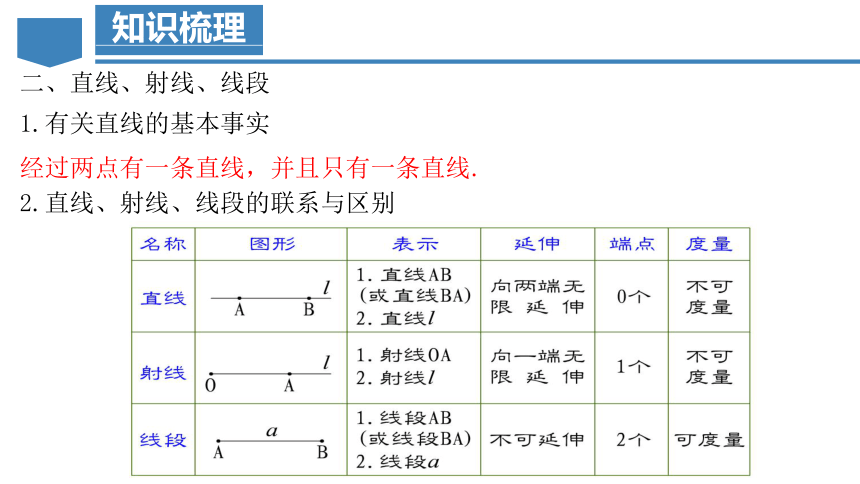
二、直线、射线、线段
1.有关直线的基本事实
经过两点有一条直线,并且只有一条直线.
2.直线、射线、线段的联系与区别
3.基本作图
(1)作一线段等于已知线段;
(2)利用尺规作图作一条线段等于两条线段的和、差.
5.有关线段的基本事实
两点之间,线段最短.
4.线段的中点
6.连接两点的线段的长度,叫做这两点间的距离.
C是线段AB的中点,
AC=BC= AB,
AB=2AC=2BC.
A
C
B
三、角
1. 角的定义
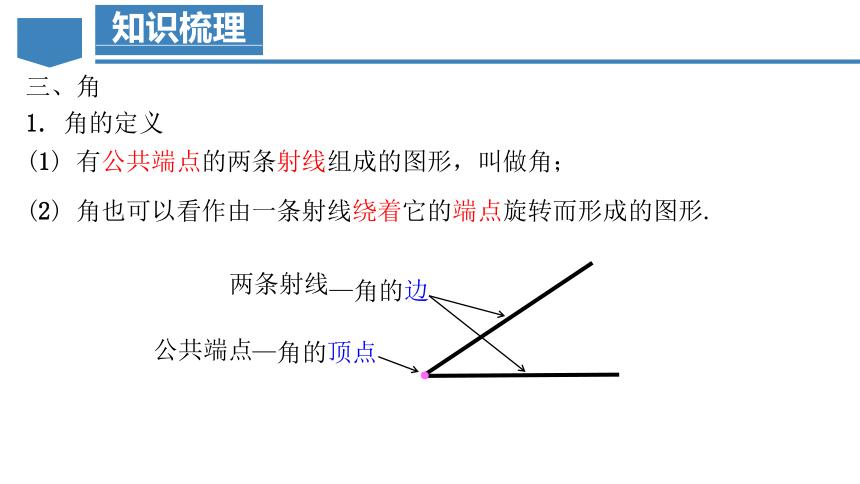
(1) 有公共端点的两条射线组成的图形,叫做角;
(2) 角也可以看作由一条射线绕着它的端点旋转而形成的图形.
公共端点
—角的顶点
两条射线
—角的边
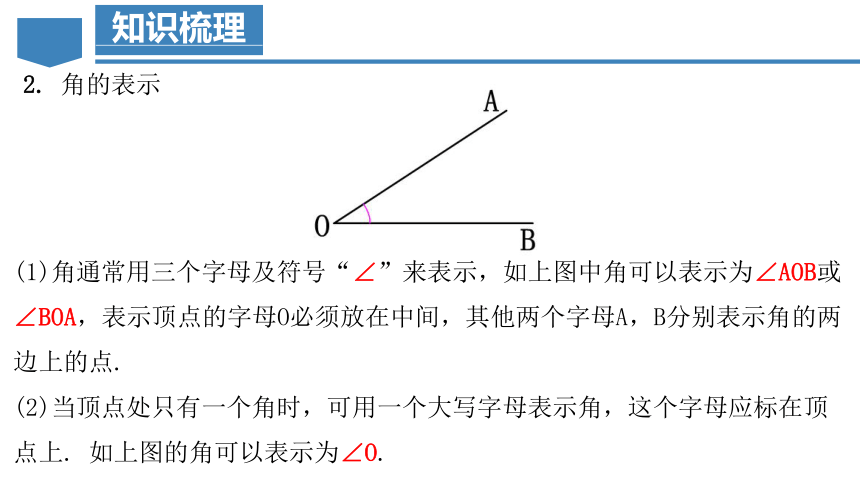
(1)角通常用三个字母及符号“∠”来表示,如上图中角可以表示为∠AOB或∠BOA,表示顶点的字母O必须放在中间,其他两个字母A,B分别表示角的两边上的点.
(2)当顶点处只有一个角时,可用一个大写字母表示角,这个字母应标在顶点上. 如上图的角可以表示为∠O.
2. 角的表示
(3)用一个数字表示一个角,如左图的角可以表示为∠1.
(4)用一个字母(希腊字母α、β、γ等)表示一个角,如右图的角可以表示为∠α.
注意:这两种方法必须在图上标注后才能使用,并且只能表示单独的一个角.
2. 角的表示
1周角=____°,1平角=____°,1°=_____′,1′=_____″,
1″=_____′,1′=_____°,1°=_____″,1″=_____°.
把一个周角360等分,每一份就是1度的角,记作1°;把1度的角60等分,每一份叫做1分的角,记作1′;把1分的角60等分,每一份叫做1秒的角,记作1″.
360
180
60
60
3600
如:∠α的度数是48度56分37秒,记作:∠α=48°56′37″.
3. 角的度量
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
OB是∠AOC的平分线
4.角的平分线
∵OB是∠AOC的角平分线,
∴∠AOB=∠BOC= ∠AOC
∠AOC=2∠AOB=2∠BOC
如果两个角的和等于90°(直角),就说这两个角互为余角,即其中一个角是另一个角的余角.如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
补角的性质:同角(等角)的补角相等.
余角的性质:同角(等角)的余角相等.
5.余角和补角
6.方位角
①定义
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向.
②书写
通常要先写北或南,再写偏东或偏西
高频考点一
立体图形与平面图形的转化
1.从不同方向看立体图形
例1.如图是由5个相同的小正方体组成的立体图形,分别画出从正面、左面、上面观察得到的平面图形.
1.如图摆放的立体图形中,从上面看与从左面看得到的平面图形相同的是
( )
C
2.用若干个棱长为1的小正方体摆成如图所示的立体图形,现拿掉一个小正方体后,从正面看得到的平面图形的面积与拿掉前相同,则这个拿掉的小正方体可以是( )
A.① B.② C.③ D.④
D
高频考点一
立体图形与平面图形的转化
2.立体图形的展开与折叠
例2.如图是正方体的展开图,则原正方体相对两个面上的数的积最小是____.
-8
1.下列四个图中,是三棱柱的表面展开图的是( )
D
2.某正方体的展开图如图所示,则原正方体“中”字所在面的对面上的汉字是( )
A.国 B.的 C.我 D.梦
B
3.小明用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有( )
A.1种 B.2种 C.3种 D.4种
C
高频考点二
点、线、面、体的关系
例3.你见过一种折叠灯笼吗 它看起来是平面的,可是提起来后却变成了美丽的灯笼,这个过程可近似地用哪个数学原理来解释( )
A.点动成线 B.线动成面 C.面动成体 D.面与面相交的地方是线
C
1.(1)转动自行车的轮子,轮子上的辐条会形成一个圆面说明____________;
(2)流星划过夜空留下一条“尾巴”说明_____________;
(3)旋转一扇门,门在空中运动的痕迹说明_____________.
2.如图,将长方形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
线动成面
点动成线
面动成体
B
高频考点三
直线、射线、线段、角的有关概念、性质
例4.如图,已知平面上三点A,B,C.
(1)请画出图形:①画直线AC;②画射线BA;③画线段BC.
(2)在(1)的条件下,图中共有______条射线.
(3)比较大小:AB+AC____BC(填“>”“<”或“=”),依据是_______________________.
两点之间,线段最短
6
>
解:(1)如图,直线AC,射线BA,线段BC即为所求.
下列四种说法:①直线AB与直线BA是同一条直线;②如图,∠α可以用∠O 表示;③建筑工人在砌墙时经常在两个墙脚处分别立一根标志杆,在两根标志杆之间拉一根绳子,沿这根绳子可以砌出直的墙,依据的数学原理是两点确定一条直线;④图中小于平角的角共有7个.其中正确的是__________.
①③④
高频考点四
线段的有关计算
例5.已知线段AB=6,在直线AB上取一点C,恰好使AC=2BC,D为BC的中点,求线段AD的长.
高频考点四
线段的有关计算
例5.已知线段AB=6,在直线AB上取一点C,恰好使AC=2BC,D为BC的中点,求线段AD的长.
解:①当点C在线段AB上时,如图①.
因为AC=2BC,设BC=x,则AC=2x.
因为AB=AC+BC,所以6=2x+x,解得x=2.
所以BC=2,AC=4.
因为D是BC的中点,
所以CD=BC=1,所以AD=AC+CD=5.
高频考点四
线段的有关计算
例5.已知线段AB=6,在直线AB上取一点C,恰好使AC=2BC,D为BC的中点,求线段AD的长.
②当点C在线段AB的延长线上时,如图②.因为AC=2BC,
所以AB=AC-BC=2BC-BC=6.
所以BC=6,AC=12.
因为D是BC的中点,所以BD=BC=3.
所以AD=AB+BD=6+3=9
高频考点四
线段的有关计算
例5.已知线段AB=6,在直线AB上取一点C,恰好使AC=2BC,D为BC的中点,求线段AD的长.
③当点C在线段BA的延长线上时,AC<BC,不存在AC=2BC,
所以此种情况不存在综上所述,线段AD的长为5或9.
1.如图,点C把线段MN分成两部分,其长度比MC:CN=5:4.若P是MN的中点,PC=2cm,则MN的长为( )
A.30cm B.36cm C.40cm D.48cm
B
2.如图,点M在线段AN的延长线上,且线段MN=51,第一次操作:分别取线段 AM和AN的中点M1,N1;第二次操作:分别取线段AM1和AN1的中点M2,N2;第三次操作:分别取线段AM2和AN2的中点M3,N3……连续这样操作20次,则M20N20=
_______.
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(1)在点B的左侧作线段BC=AB,在B的右侧作线段BD=3AB(要求尺规作图,不写作法,保留作图痕迹);
(2)若点C表示的数为c,点D表示的数为d,且AB=20,求c,d的值;
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(1)在点B的左侧作线段BC=AB,在B的右侧作线段BD=3AB(要求尺规作图,不写作法,保留作图痕迹);
(2)若点C表示的数为c,点D表示的数为d,且AB=20,求c,d的值;
解:(1)如图,线段BC,BD为所求线段
(2)因为AB=20,BC=AB,BD=3AB
所以AC=2AB=40,AD=BD-AB=2AB=40.
因为a=12,所以c=12-40=-28,d=12+40=52
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
(3)分两种情况讨论:
①点N在线段CD上,由(2)得CD=d-c=52-(-28)=80,点B对应的数为b=a-20= 12-20=-8,所以BD=d-b=52-(-8)=60.
因为M是BD的中点,
所以点M对应的数为d-30=52-30=22.
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
因为CN=2DN,所以DN=CD=,
所以点N对应的数为52->22,
所以MN=-22=.
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
②点N在线段CD的延长线上,
因为CN=2DN,所以DN=CD=80,
所以点N对应的数为d+80=52+80=132.
所以MN=132-22=110.
故 MN的长为或110.
高频考点五
角的有关计算
例6.如图,OM平分∠AOB,ON为∠AOM内的一条射线.
(1)若∠BON=55°,∠AON=15°求∠MON的度数.
(2)小明得出一个关系式: ∠MON=(∠BON-∠AON),你认为这个关系式正确吗 请说明理由.
高频考点五
角的有关计算
例6.如图,OM平分∠AOB,ON为∠AOM内的一条射线.
(1)若∠BON=55°,∠AON=15°求∠MON的度数.
高频考点五
角的有关计算
例6.如图,OM平分∠AOB,ON为∠AOM内的一条射线.
(1)若∠BON=55°,∠AON=15°求∠MON的度数.
解:(1)因为∠BON=55°,∠AON=15°,
所以∠AOB=∠AON+∠BON=70°
因为OM平分∠AOB
所以∠AOM=∠AOB=35°
所以∠MON=∠AOM-∠AON=20°
高频考点五
角的有关计算
(2)小明得出一个关系式: ∠MON=(∠BON-∠AON),你认为这个关系式正确吗 请说明理由.
(2)正确.理由如下:
∠MON=∠AOM-∠AON=∠AOB-∠AON
=(∠AON+∠BON)-∠AON
=(∠BON-∠AON).
1.如图,将量角器的中心与∠AOB的顶点重合,射线OA,OB分别经过刻度18和140,把∠AOB绕点O旋转到∠A′OB′,∠AOA′的平分线OC经过刻度32,则∠AOB′的平分线经过的刻度是_______.
93
2.如图①,点0在直线AB上,∠BOC=40°,∠COE=90°,作射线OD,使∠AOC=2∠AOD,求∠DOE的度数.甲同学给出以下解答过程.
解:如图②,因为∠AOB=180°,∠BOC=40°,
所以∠AOC=______°.
因为∠AOC=2∠AOD,
所以OD平分∠AOC.
所以∠COD=∠AOC=_____°.
因为∠COE=90°,
所以∠DOE=∠COD+∠COE=______°.
140
70
160
(1)请将甲同学的解答过程补充完整.
(2)乙同学认为还有一种情况,你认为乙同学的说法是否正确.若正确,请求∠DOE的度数;若不正确,请说明理由.
(2)乙同学的说法正确.
当OD在∠AOC外部时,如图,
因为点O在直线AB上,
所以∠AOB=180°.
因为∠BOC=40°,
所以∠AOC=∠AOB-∠BOC=140°.
(1)请将甲同学的解答过程补充完整.
(2)乙同学认为还有一种情况,你认为乙同学的说法是否正确.若正确,请求∠DOE的度数;若不正确,请说明理由.
因为∠AOC=2∠AOD,
所以∠AOD=-∠AOC=70°.
因为∠COE=90°,
所以∠BOE=∠COE-∠BOC=50°,
所以∠DOE=∠AOB-∠AOD-∠BOE=60°.
综上所述,∠DOE的度数是160°或60°.
高频考点六
余角和补角、方位角、钟面角
例7.如图,将一副三角板按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A
1.钟面上7时30分时,时针与分针的夹角的度数是_______.
2.如图,射线OB表示北偏西20°方向,射线OC表示南偏东60°方向,OA平分∠BOC,射线OA表示( )方向.
A.北偏东50° B.北偏东70° C.北偏东45° D.北偏东60°
45°
B
3.一个角的余角等于它的补角的,求这个角的度数.
解:设这个角的度数为x°.
由题意,得90-x=(180-x) ,
解得x=60.
故这个角的度数为60°.
易错考点一
由展开图还原立体图形出错
例1.将如图的平面图形经过折叠得到的正方体(图案露在外面)是( )
C
易错考点二
对有关概念理解不透彻
例2.下列说法正确的有( )
①延长射线0A到点C;②连接两点间的线段叫做这两点的距离;③锐角和钝角互补;④如果两个角是同一个角的余角,那么这两个角相等.
A.1个 B.2个 C.3个 D.4个
A
易错考点三
角度换算错误
例3.比较大小: 14°15′_____14.15°. (填“>”“<”或“=”)
正解:14°15′=14.25°.
因为14.25°>14.15°,
所以14°15′>14.15°.
>
易错考点四
没有分类讨论导致漏解
例4.已知射线0A,若从点O引两条射线OB,OC,使∠AOB=50°,∠BOC=20°,
求∠AOC的度数.
正解:①当0C在∠AOB的外部时,如图①,∠AOC=∠AOB+∠BOC=50°+20°=70°;
当OC在∠AOB的内部时,如图②,
∠AOC=∠AOB-∠BOC=50°-20°=30°.
综上所述,∠AOC的度数为70°或30°.
单元小结
第四单元
第4章 几何图形初步
01
03
04
02
05
举一反三
知识梳理
易错考点
高频考点
章节框图
一、几何图形
1. 立体图形与平面图形
(1)立体图形的各部分不都在同一平面内,如:
(2)平面图形的各部分都在同一平面内,如:
常见立体图形
柱体
锥体
球体
圆柱
棱柱
三棱柱
四棱柱
五棱柱
…
圆锥
棱锥
三棱锥
四棱锥
五棱锥
…
2.常见立体图形的分类
(命名依据底面的边数)
(命名依据底面的边数)
我们从不同的方向观察一物体时,可能看到不同的图形. 其中,把从正面看到的图叫做主视图,把从左面看到的图叫做左视图,从上面看到的图叫做俯视图.
(注:俯视图通常画在主视图的下面,左视图通常画在主视图的右面)
3.从不同方向看立体图形
一四一型
6种
二三一型
3种
二二二型
1种
三三型
1种
4.立体图形的展开图
5.点、线、面、体之间的联系
(1) 体是由面围成,面与面相交成线,线与线相交成点;
(2) 点动成线、线动成面、面动成体.
二、直线、射线、线段
1.有关直线的基本事实
经过两点有一条直线,并且只有一条直线.
2.直线、射线、线段的联系与区别
3.基本作图
(1)作一线段等于已知线段;
(2)利用尺规作图作一条线段等于两条线段的和、差.
5.有关线段的基本事实
两点之间,线段最短.
4.线段的中点
6.连接两点的线段的长度,叫做这两点间的距离.
C是线段AB的中点,
AC=BC= AB,
AB=2AC=2BC.
A
C
B
三、角
1. 角的定义
(1) 有公共端点的两条射线组成的图形,叫做角;
(2) 角也可以看作由一条射线绕着它的端点旋转而形成的图形.
公共端点
—角的顶点
两条射线
—角的边
(1)角通常用三个字母及符号“∠”来表示,如上图中角可以表示为∠AOB或∠BOA,表示顶点的字母O必须放在中间,其他两个字母A,B分别表示角的两边上的点.
(2)当顶点处只有一个角时,可用一个大写字母表示角,这个字母应标在顶点上. 如上图的角可以表示为∠O.
2. 角的表示
(3)用一个数字表示一个角,如左图的角可以表示为∠1.
(4)用一个字母(希腊字母α、β、γ等)表示一个角,如右图的角可以表示为∠α.
注意:这两种方法必须在图上标注后才能使用,并且只能表示单独的一个角.
2. 角的表示
1周角=____°,1平角=____°,1°=_____′,1′=_____″,
1″=_____′,1′=_____°,1°=_____″,1″=_____°.
把一个周角360等分,每一份就是1度的角,记作1°;把1度的角60等分,每一份叫做1分的角,记作1′;把1分的角60等分,每一份叫做1秒的角,记作1″.
360
180
60
60
3600
如:∠α的度数是48度56分37秒,记作:∠α=48°56′37″.
3. 角的度量
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
OB是∠AOC的平分线
4.角的平分线
∵OB是∠AOC的角平分线,
∴∠AOB=∠BOC= ∠AOC
∠AOC=2∠AOB=2∠BOC
如果两个角的和等于90°(直角),就说这两个角互为余角,即其中一个角是另一个角的余角.如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
补角的性质:同角(等角)的补角相等.
余角的性质:同角(等角)的余角相等.
5.余角和补角
6.方位角
①定义
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向.
②书写
通常要先写北或南,再写偏东或偏西
高频考点一
立体图形与平面图形的转化
1.从不同方向看立体图形
例1.如图是由5个相同的小正方体组成的立体图形,分别画出从正面、左面、上面观察得到的平面图形.
1.如图摆放的立体图形中,从上面看与从左面看得到的平面图形相同的是
( )
C
2.用若干个棱长为1的小正方体摆成如图所示的立体图形,现拿掉一个小正方体后,从正面看得到的平面图形的面积与拿掉前相同,则这个拿掉的小正方体可以是( )
A.① B.② C.③ D.④
D
高频考点一
立体图形与平面图形的转化
2.立体图形的展开与折叠
例2.如图是正方体的展开图,则原正方体相对两个面上的数的积最小是____.
-8
1.下列四个图中,是三棱柱的表面展开图的是( )
D
2.某正方体的展开图如图所示,则原正方体“中”字所在面的对面上的汉字是( )
A.国 B.的 C.我 D.梦
B
3.小明用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有( )
A.1种 B.2种 C.3种 D.4种
C
高频考点二
点、线、面、体的关系
例3.你见过一种折叠灯笼吗 它看起来是平面的,可是提起来后却变成了美丽的灯笼,这个过程可近似地用哪个数学原理来解释( )
A.点动成线 B.线动成面 C.面动成体 D.面与面相交的地方是线
C
1.(1)转动自行车的轮子,轮子上的辐条会形成一个圆面说明____________;
(2)流星划过夜空留下一条“尾巴”说明_____________;
(3)旋转一扇门,门在空中运动的痕迹说明_____________.
2.如图,将长方形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
线动成面
点动成线
面动成体
B
高频考点三
直线、射线、线段、角的有关概念、性质
例4.如图,已知平面上三点A,B,C.
(1)请画出图形:①画直线AC;②画射线BA;③画线段BC.
(2)在(1)的条件下,图中共有______条射线.
(3)比较大小:AB+AC____BC(填“>”“<”或“=”),依据是_______________________.
两点之间,线段最短
6
>
解:(1)如图,直线AC,射线BA,线段BC即为所求.
下列四种说法:①直线AB与直线BA是同一条直线;②如图,∠α可以用∠O 表示;③建筑工人在砌墙时经常在两个墙脚处分别立一根标志杆,在两根标志杆之间拉一根绳子,沿这根绳子可以砌出直的墙,依据的数学原理是两点确定一条直线;④图中小于平角的角共有7个.其中正确的是__________.
①③④
高频考点四
线段的有关计算
例5.已知线段AB=6,在直线AB上取一点C,恰好使AC=2BC,D为BC的中点,求线段AD的长.
高频考点四
线段的有关计算
例5.已知线段AB=6,在直线AB上取一点C,恰好使AC=2BC,D为BC的中点,求线段AD的长.
解:①当点C在线段AB上时,如图①.
因为AC=2BC,设BC=x,则AC=2x.
因为AB=AC+BC,所以6=2x+x,解得x=2.
所以BC=2,AC=4.
因为D是BC的中点,
所以CD=BC=1,所以AD=AC+CD=5.
高频考点四
线段的有关计算
例5.已知线段AB=6,在直线AB上取一点C,恰好使AC=2BC,D为BC的中点,求线段AD的长.
②当点C在线段AB的延长线上时,如图②.因为AC=2BC,
所以AB=AC-BC=2BC-BC=6.
所以BC=6,AC=12.
因为D是BC的中点,所以BD=BC=3.
所以AD=AB+BD=6+3=9
高频考点四
线段的有关计算
例5.已知线段AB=6,在直线AB上取一点C,恰好使AC=2BC,D为BC的中点,求线段AD的长.
③当点C在线段BA的延长线上时,AC<BC,不存在AC=2BC,
所以此种情况不存在综上所述,线段AD的长为5或9.
1.如图,点C把线段MN分成两部分,其长度比MC:CN=5:4.若P是MN的中点,PC=2cm,则MN的长为( )
A.30cm B.36cm C.40cm D.48cm
B
2.如图,点M在线段AN的延长线上,且线段MN=51,第一次操作:分别取线段 AM和AN的中点M1,N1;第二次操作:分别取线段AM1和AN1的中点M2,N2;第三次操作:分别取线段AM2和AN2的中点M3,N3……连续这样操作20次,则M20N20=
_______.
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(1)在点B的左侧作线段BC=AB,在B的右侧作线段BD=3AB(要求尺规作图,不写作法,保留作图痕迹);
(2)若点C表示的数为c,点D表示的数为d,且AB=20,求c,d的值;
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(1)在点B的左侧作线段BC=AB,在B的右侧作线段BD=3AB(要求尺规作图,不写作法,保留作图痕迹);
(2)若点C表示的数为c,点D表示的数为d,且AB=20,求c,d的值;
解:(1)如图,线段BC,BD为所求线段
(2)因为AB=20,BC=AB,BD=3AB
所以AC=2AB=40,AD=BD-AB=2AB=40.
因为a=12,所以c=12-40=-28,d=12+40=52
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
(3)分两种情况讨论:
①点N在线段CD上,由(2)得CD=d-c=52-(-28)=80,点B对应的数为b=a-20= 12-20=-8,所以BD=d-b=52-(-8)=60.
因为M是BD的中点,
所以点M对应的数为d-30=52-30=22.
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
因为CN=2DN,所以DN=CD=,
所以点N对应的数为52->22,
所以MN=-22=.
3.如图,已知数轴上有两点A,B,它们表示的数分别为a,b,其中a=12.
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
②点N在线段CD的延长线上,
因为CN=2DN,所以DN=CD=80,
所以点N对应的数为d+80=52+80=132.
所以MN=132-22=110.
故 MN的长为或110.
高频考点五
角的有关计算
例6.如图,OM平分∠AOB,ON为∠AOM内的一条射线.
(1)若∠BON=55°,∠AON=15°求∠MON的度数.
(2)小明得出一个关系式: ∠MON=(∠BON-∠AON),你认为这个关系式正确吗 请说明理由.
高频考点五
角的有关计算
例6.如图,OM平分∠AOB,ON为∠AOM内的一条射线.
(1)若∠BON=55°,∠AON=15°求∠MON的度数.
高频考点五
角的有关计算
例6.如图,OM平分∠AOB,ON为∠AOM内的一条射线.
(1)若∠BON=55°,∠AON=15°求∠MON的度数.
解:(1)因为∠BON=55°,∠AON=15°,
所以∠AOB=∠AON+∠BON=70°
因为OM平分∠AOB
所以∠AOM=∠AOB=35°
所以∠MON=∠AOM-∠AON=20°
高频考点五
角的有关计算
(2)小明得出一个关系式: ∠MON=(∠BON-∠AON),你认为这个关系式正确吗 请说明理由.
(2)正确.理由如下:
∠MON=∠AOM-∠AON=∠AOB-∠AON
=(∠AON+∠BON)-∠AON
=(∠BON-∠AON).
1.如图,将量角器的中心与∠AOB的顶点重合,射线OA,OB分别经过刻度18和140,把∠AOB绕点O旋转到∠A′OB′,∠AOA′的平分线OC经过刻度32,则∠AOB′的平分线经过的刻度是_______.
93
2.如图①,点0在直线AB上,∠BOC=40°,∠COE=90°,作射线OD,使∠AOC=2∠AOD,求∠DOE的度数.甲同学给出以下解答过程.
解:如图②,因为∠AOB=180°,∠BOC=40°,
所以∠AOC=______°.
因为∠AOC=2∠AOD,
所以OD平分∠AOC.
所以∠COD=∠AOC=_____°.
因为∠COE=90°,
所以∠DOE=∠COD+∠COE=______°.
140
70
160
(1)请将甲同学的解答过程补充完整.
(2)乙同学认为还有一种情况,你认为乙同学的说法是否正确.若正确,请求∠DOE的度数;若不正确,请说明理由.
(2)乙同学的说法正确.
当OD在∠AOC外部时,如图,
因为点O在直线AB上,
所以∠AOB=180°.
因为∠BOC=40°,
所以∠AOC=∠AOB-∠BOC=140°.
(1)请将甲同学的解答过程补充完整.
(2)乙同学认为还有一种情况,你认为乙同学的说法是否正确.若正确,请求∠DOE的度数;若不正确,请说明理由.
因为∠AOC=2∠AOD,
所以∠AOD=-∠AOC=70°.
因为∠COE=90°,
所以∠BOE=∠COE-∠BOC=50°,
所以∠DOE=∠AOB-∠AOD-∠BOE=60°.
综上所述,∠DOE的度数是160°或60°.
高频考点六
余角和补角、方位角、钟面角
例7.如图,将一副三角板按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A
1.钟面上7时30分时,时针与分针的夹角的度数是_______.
2.如图,射线OB表示北偏西20°方向,射线OC表示南偏东60°方向,OA平分∠BOC,射线OA表示( )方向.
A.北偏东50° B.北偏东70° C.北偏东45° D.北偏东60°
45°
B
3.一个角的余角等于它的补角的,求这个角的度数.
解:设这个角的度数为x°.
由题意,得90-x=(180-x) ,
解得x=60.
故这个角的度数为60°.
易错考点一
由展开图还原立体图形出错
例1.将如图的平面图形经过折叠得到的正方体(图案露在外面)是( )
C
易错考点二
对有关概念理解不透彻
例2.下列说法正确的有( )
①延长射线0A到点C;②连接两点间的线段叫做这两点的距离;③锐角和钝角互补;④如果两个角是同一个角的余角,那么这两个角相等.
A.1个 B.2个 C.3个 D.4个
A
易错考点三
角度换算错误
例3.比较大小: 14°15′_____14.15°. (填“>”“<”或“=”)
正解:14°15′=14.25°.
因为14.25°>14.15°,
所以14°15′>14.15°.
>
易错考点四
没有分类讨论导致漏解
例4.已知射线0A,若从点O引两条射线OB,OC,使∠AOB=50°,∠BOC=20°,
求∠AOC的度数.
正解:①当0C在∠AOB的外部时,如图①,∠AOC=∠AOB+∠BOC=50°+20°=70°;
当OC在∠AOB的内部时,如图②,
∠AOC=∠AOB-∠BOC=50°-20°=30°.
综上所述,∠AOC的度数为70°或30°.
