5 数学广角——鸽巢问题课件六年级下册数学人教版(共15张PPT)
文档属性
| 名称 | 5 数学广角——鸽巢问题课件六年级下册数学人教版(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
若安 老师
5.1 数学广角——鸽巢问题(一)
人教版六年级下册第五单元
情景导入
游戏引入 激发兴趣
游戏名称:抢坐椅子
游戏准备: 4名同学,抢坐3把椅子
游戏规则:三把椅子背靠背,四人围着椅子转,当老师说停止时快速坐到椅子上,不管什么情况,每个同学都要坐下。
观察结果:每次总有一把椅子要坐2人
若安 老师
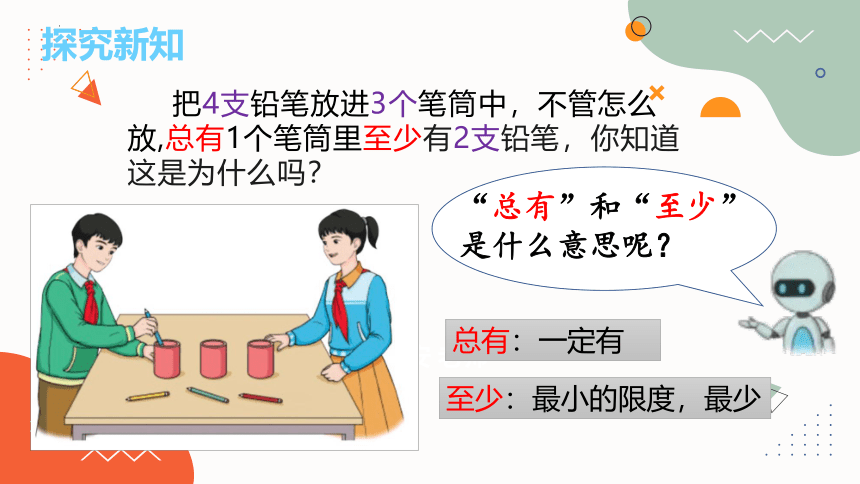
把4支铅笔放进3个笔筒中,不管怎么放,总有1个笔筒里至少有2支铅笔,你知道这是为什么吗?
“总有”和“至少”是什么意思呢?
探究新知
总有:一定有
至少:最小的限度,最少
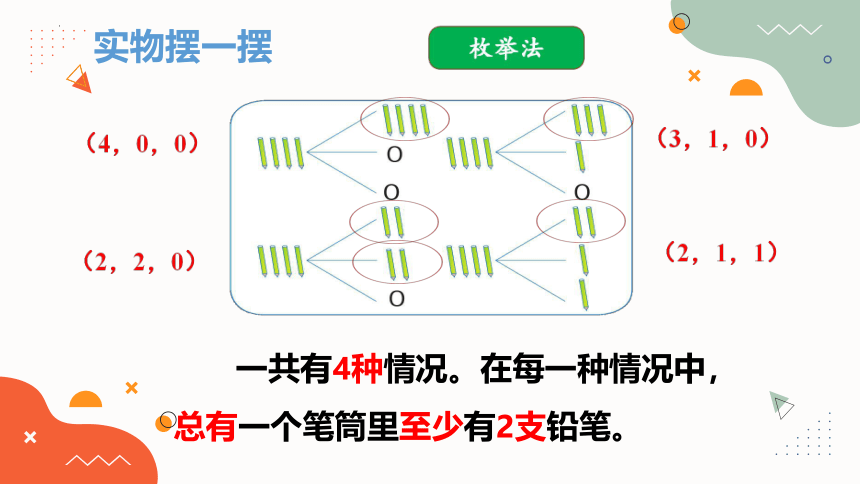
实物摆一摆
一共有4种情况。在每一种情况中,
总有一个笔筒里至少有2支铅笔。
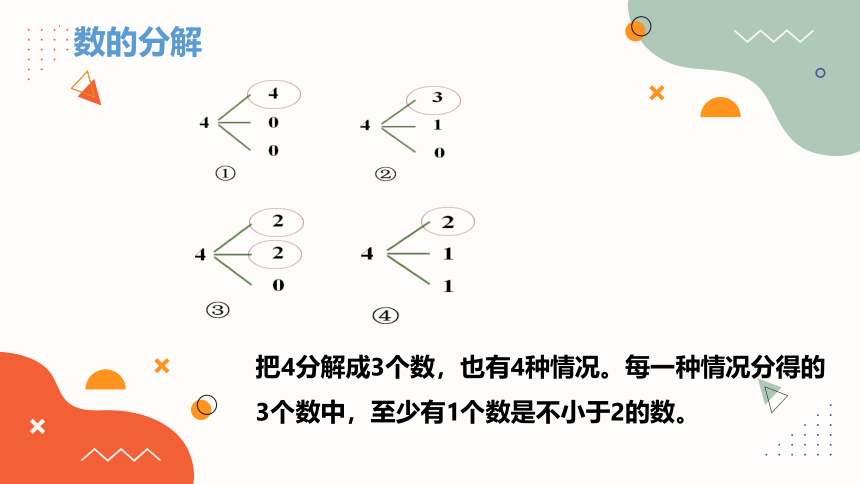
数的分解
把4分解成3个数,也有4种情况。每一种情况分得的
3个数中,至少有1个数是不小于2的数。
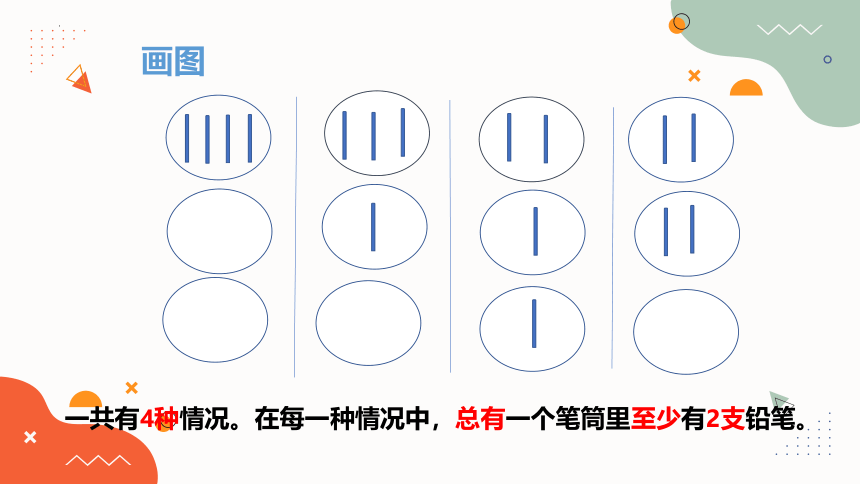
画图
一共有4种情况。在每一种情况中,总有一个笔筒里至少有2支铅笔。
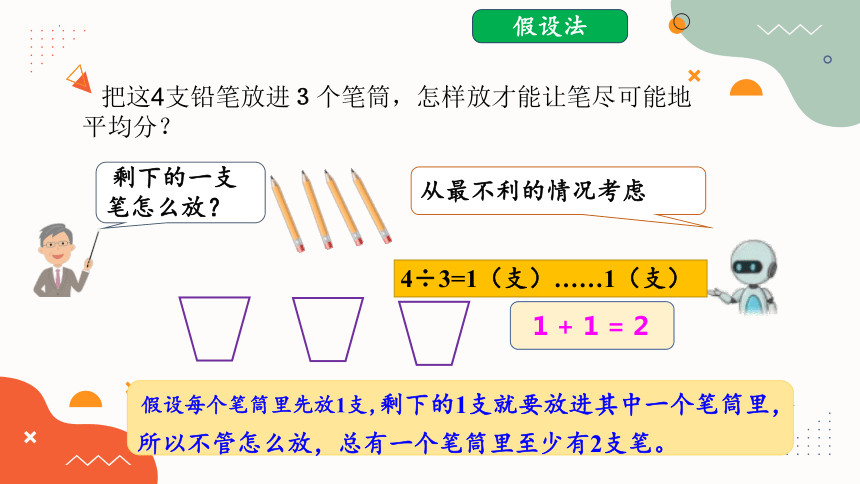
假设法
把这4支铅笔放进3个笔筒,怎样放才能让笔尽可能地平均分?
所以不管怎么放,总有一个笔筒里至少有2支笔。
剩下的1支就要放进其中一个笔筒里,
假设每个笔筒里先放1支,
从最不利的情况考虑
剩下的一支 笔怎么放?
1+1=2
4÷3=1(支)……1(支)
认识鸽巢问题
像前面这样的问题就是“鸽巢问题”,它里面蕴涵的数学原理就叫做“鸽巢原理”。
鸽巢问题
物体
4支铅笔
4个要分放的物体
鸽巢
3 个笔筒
3个鸽巢
提升思维,构建模型
把5支铅笔放进4 个盒子里,总有一个盒子至少放进几支铅笔?
鸽巢
物体
5 ÷4=1(支) … …1(支)
用前面你喜欢的方法试着验证一下。
1+1=2(支)
铅笔支数 盒子个数 总有一个盒子里至少放的铅笔数
6
n
…
…
5
7
6
8
7
9
8
N+1
2
2
2
2
2
归纳、推理、总结
得出结论:
只要放的铅笔数比笔筒的数量多,总有1个笔筒里至少放进2支铅笔
把m个物体任意放进n个鸽巢中(m和n是非0自然数,且m>n),那么一定有一个鸽巢里至少放进了2个物体。
只要铅笔的支数比笔筒数多,总有一个笔筒里至少放进2支铅笔。
鸽巢原理(一)
分组讨论:如果铅笔的支数比笔筒的数量多2、多3、多4,那么,总有一个笔筒里至少放入几支铅笔?
拓展模型、解释应用
课堂收获
枚举和假设,都是解决问题的好办法。
从最不利的角度去思考
解决这类问题的经验以后也可以帮助我们解决其他问题。
归纳、推理、总结,是学习数学的好方法
课堂练习
“鸽子”数:13
随意找13位老师,他们中至少有2个人的属相相同。为什么
13÷12=1(个)……1(个)
“鸽巢”数:12
1+1=2(个)
课后巩固
数学书第67页做一做第2题
数学书第67页做一做第2题
数学书第67页做一做第1、2题
若安 老师
5.1 数学广角——鸽巢问题(一)
人教版六年级下册第五单元
情景导入
游戏引入 激发兴趣
游戏名称:抢坐椅子
游戏准备: 4名同学,抢坐3把椅子
游戏规则:三把椅子背靠背,四人围着椅子转,当老师说停止时快速坐到椅子上,不管什么情况,每个同学都要坐下。
观察结果:每次总有一把椅子要坐2人
若安 老师
把4支铅笔放进3个笔筒中,不管怎么放,总有1个笔筒里至少有2支铅笔,你知道这是为什么吗?
“总有”和“至少”是什么意思呢?
探究新知
总有:一定有
至少:最小的限度,最少
实物摆一摆
一共有4种情况。在每一种情况中,
总有一个笔筒里至少有2支铅笔。
数的分解
把4分解成3个数,也有4种情况。每一种情况分得的
3个数中,至少有1个数是不小于2的数。
画图
一共有4种情况。在每一种情况中,总有一个笔筒里至少有2支铅笔。
假设法
把这4支铅笔放进3个笔筒,怎样放才能让笔尽可能地平均分?
所以不管怎么放,总有一个笔筒里至少有2支笔。
剩下的1支就要放进其中一个笔筒里,
假设每个笔筒里先放1支,
从最不利的情况考虑
剩下的一支 笔怎么放?
1+1=2
4÷3=1(支)……1(支)
认识鸽巢问题
像前面这样的问题就是“鸽巢问题”,它里面蕴涵的数学原理就叫做“鸽巢原理”。
鸽巢问题
物体
4支铅笔
4个要分放的物体
鸽巢
3 个笔筒
3个鸽巢
提升思维,构建模型
把5支铅笔放进4 个盒子里,总有一个盒子至少放进几支铅笔?
鸽巢
物体
5 ÷4=1(支) … …1(支)
用前面你喜欢的方法试着验证一下。
1+1=2(支)
铅笔支数 盒子个数 总有一个盒子里至少放的铅笔数
6
n
…
…
5
7
6
8
7
9
8
N+1
2
2
2
2
2
归纳、推理、总结
得出结论:
只要放的铅笔数比笔筒的数量多,总有1个笔筒里至少放进2支铅笔
把m个物体任意放进n个鸽巢中(m和n是非0自然数,且m>n),那么一定有一个鸽巢里至少放进了2个物体。
只要铅笔的支数比笔筒数多,总有一个笔筒里至少放进2支铅笔。
鸽巢原理(一)
分组讨论:如果铅笔的支数比笔筒的数量多2、多3、多4,那么,总有一个笔筒里至少放入几支铅笔?
拓展模型、解释应用
课堂收获
枚举和假设,都是解决问题的好办法。
从最不利的角度去思考
解决这类问题的经验以后也可以帮助我们解决其他问题。
归纳、推理、总结,是学习数学的好方法
课堂练习
“鸽子”数:13
随意找13位老师,他们中至少有2个人的属相相同。为什么
13÷12=1(个)……1(个)
“鸽巢”数:12
1+1=2(个)
课后巩固
数学书第67页做一做第2题
数学书第67页做一做第2题
数学书第67页做一做第1、2题
