陕西省西安市碑林区2022-2023学年高二下学期期末考试理科数学试题(扫描版无答案)
文档属性
| 名称 | 陕西省西安市碑林区2022-2023学年高二下学期期末考试理科数学试题(扫描版无答案) |  | |
| 格式 | |||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 11:48:42 | ||
图片预览

文档简介
2022-2023-2高二年级期末考试
(理科)试题
时间:120分满分:150分
一.选释题.本题共12小题每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的.
1若高一(1)班参加田赛的学生有15人,参加径赛的学生有13人,两项都参加的有5人,那么高一
(1)班参加本次运动会的人数共有()
A.28
B.23
C.18
D.16
2若命器:x∈R。'2<0,则-力衣运准确的是()
A3xeR12≥0
20
x-2
B.∈R
x-2
c.reR,1,>0或x=2
>0或x=2
x-2
D,冰eR
x-2
x=3-tsin 20'
3.已知直线的参数方程为
(t为参数),则该直线的倾斜角为()
y=2+tc0s70°
A20°
B.45°
C.110
D.135
4若国写P闭=号,P到-写
2
则事件A与B的关系是()
A相互独立
B对立
C,互斥但不对立
D.既互斥又独立
5.已知向量a=(1,2),b=(2+x,1-y),且a1b,则2y-x的值为()
A.-4
B.-3
C.0
D.4
6t+e+克
展开式中x4项的系数为()
A.6
B.7
c.8
D.9
7.已知数列{a,}的通项公式为a。=97-3n(n∈N),那么当数列{a,a4,2{neN)的前n项和取得最大
值时,n的值为()
A.30
B31
C32
D.33
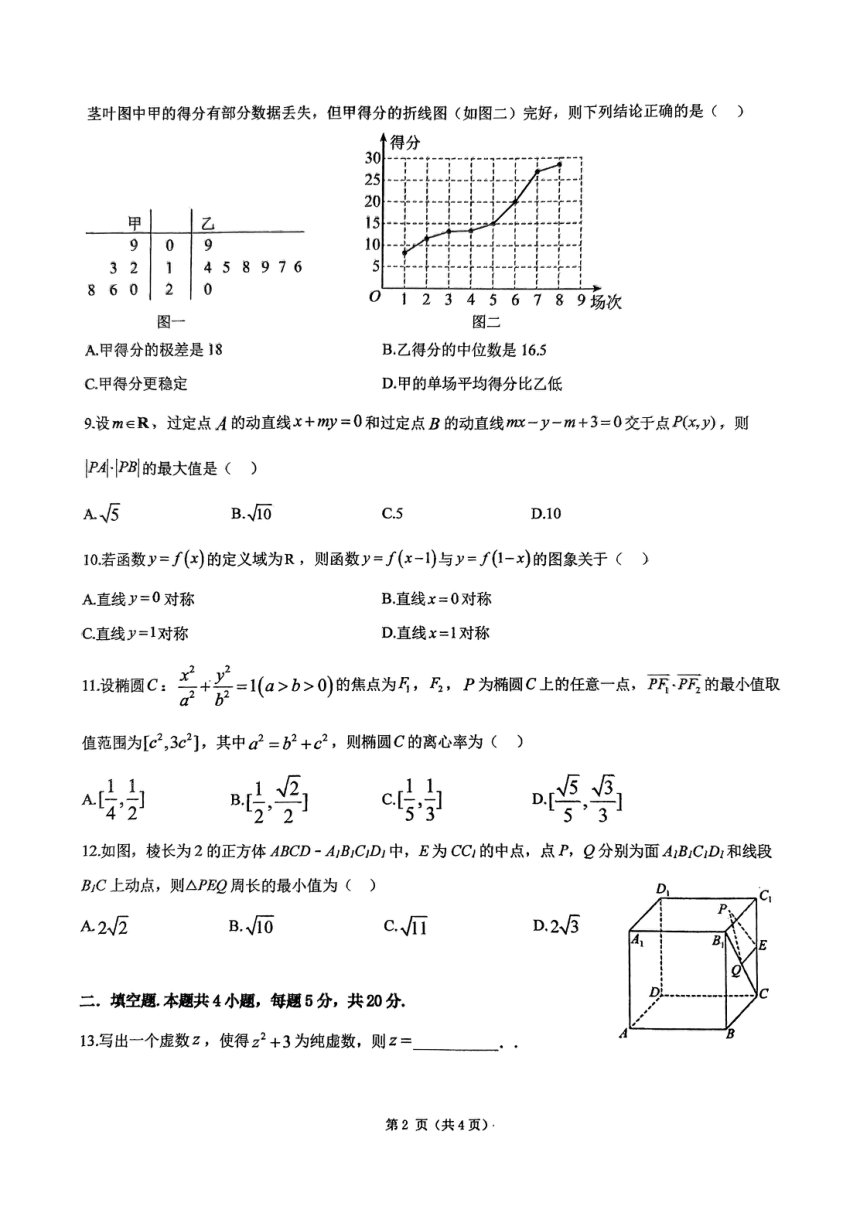
8,在某校高中篮球联赛中,某班甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(如图一),
第1页(共4页)
茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(如图二)完好,则下列结论正确的是()
得分
30
25
20
甲
15
0
9
10
32
1
458976
5
860
2
0
123456789场次
图一
图二
A.甲得分的极差是18
B.乙得分的中位数是16.5
C.甲得分更稳定
D.甲的单场平均得分比乙低
9.设m∈R,过定点A的动直线x+y=O和过定点B的动直线m一y-m+3=0交于点P(x,y),则
PAPB的最大值是()
A.5
B.√10
C.5
D.10
10.若函数y=f(x)的定义域为R,则函数y=f(x-1)与y=f(1-x)的图象关于)
A直线y=0对称
B.直线x=0对称
C.直线y=1对称
D.直线x兰1对称
11.设椭圆C:
产+存=1(a>b>0)的焦点为,B,P为椭圆C上的任意一点,P丙丽的最小值取
值范围为[c2,3c2],其中a2=b2+c2,则椭圆C的离心率为()
12如图,棱长为2的正方体ABCD-A1BCD!巾,E为CC,的中点,点P,Q分别为面ABCD!和线段
BC上动点,则△PE2周长的最小值为()
D
A22
B.10
c.1
D.25
二.填空题.本题共4小题,每题5分,共20分.
13.写出一个虚数z,使得z2+3为纯虚数,则z=
第2页(共4页)
(理科)试题
时间:120分满分:150分
一.选释题.本题共12小题每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的.
1若高一(1)班参加田赛的学生有15人,参加径赛的学生有13人,两项都参加的有5人,那么高一
(1)班参加本次运动会的人数共有()
A.28
B.23
C.18
D.16
2若命器:x∈R。'2<0,则-力衣运准确的是()
A3xeR12≥0
20
x-2
B.∈R
x-2
c.reR,1,>0或x=2
>0或x=2
x-2
D,冰eR
x-2
x=3-tsin 20'
3.已知直线的参数方程为
(t为参数),则该直线的倾斜角为()
y=2+tc0s70°
A20°
B.45°
C.110
D.135
4若国写P闭=号,P到-写
2
则事件A与B的关系是()
A相互独立
B对立
C,互斥但不对立
D.既互斥又独立
5.已知向量a=(1,2),b=(2+x,1-y),且a1b,则2y-x的值为()
A.-4
B.-3
C.0
D.4
6t+e+克
展开式中x4项的系数为()
A.6
B.7
c.8
D.9
7.已知数列{a,}的通项公式为a。=97-3n(n∈N),那么当数列{a,a4,2{neN)的前n项和取得最大
值时,n的值为()
A.30
B31
C32
D.33
8,在某校高中篮球联赛中,某班甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(如图一),
第1页(共4页)
茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(如图二)完好,则下列结论正确的是()
得分
30
25
20
甲
15
0
9
10
32
1
458976
5
860
2
0
123456789场次
图一
图二
A.甲得分的极差是18
B.乙得分的中位数是16.5
C.甲得分更稳定
D.甲的单场平均得分比乙低
9.设m∈R,过定点A的动直线x+y=O和过定点B的动直线m一y-m+3=0交于点P(x,y),则
PAPB的最大值是()
A.5
B.√10
C.5
D.10
10.若函数y=f(x)的定义域为R,则函数y=f(x-1)与y=f(1-x)的图象关于)
A直线y=0对称
B.直线x=0对称
C.直线y=1对称
D.直线x兰1对称
11.设椭圆C:
产+存=1(a>b>0)的焦点为,B,P为椭圆C上的任意一点,P丙丽的最小值取
值范围为[c2,3c2],其中a2=b2+c2,则椭圆C的离心率为()
12如图,棱长为2的正方体ABCD-A1BCD!巾,E为CC,的中点,点P,Q分别为面ABCD!和线段
BC上动点,则△PE2周长的最小值为()
D
A22
B.10
c.1
D.25
二.填空题.本题共4小题,每题5分,共20分.
13.写出一个虚数z,使得z2+3为纯虚数,则z=
第2页(共4页)
同课章节目录
