四则运算-括号课件四年级下册数学人教版(共17张PPT)
文档属性
| 名称 | 四则运算-括号课件四年级下册数学人教版(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 12:50:47 | ||
图片预览






文档简介
(共17张PPT)
四则运算—括号
说一说下面算式的运算顺序。
A组 35-23+18 75+40-26
B组 34×15÷20 63÷9×24
C组 46-18×5 56÷8+5
D组 12×24-32÷8 63÷21+12×6
课前热身
观察A、B、C、D四组算式,你发现每组两个算式的运算顺序有什么共同的特点?
先乘除后加减、只有加减或者乘除的时候,从左往右依次计算,这些都是四则混合运算当中的法则。
四则混合运算
通常把4种运算统称为:
感受括号的作用
感受小括号的作用
2. 如果变成96÷(12+4)×2,运算顺序怎样?
3. 先说一说运算的顺序,再计算。
96÷12+4×2
问题:1. 说一说这道题的运算顺序是什么。
要先算小括号里面的。
预设:96÷(12+4)×2
=96÷16×2
=6×2
=12
思考与交流:如果想改变96÷ (12+4)×2 的运算顺序:先算加法,再算乘法,最后算除法,应该怎么办?
引入中括号
个算式用了小括号后,还需要改变运算顺序,就要使用中括号。
96÷[(12+4)×2]
( )
符号“[ ]”是中括号。它的作用与小括号一样,也是改变
混合运算的运算顺序,中括号要用在小括号的外面。当一
96÷[(12+4)×2]
=96÷
=96
=3
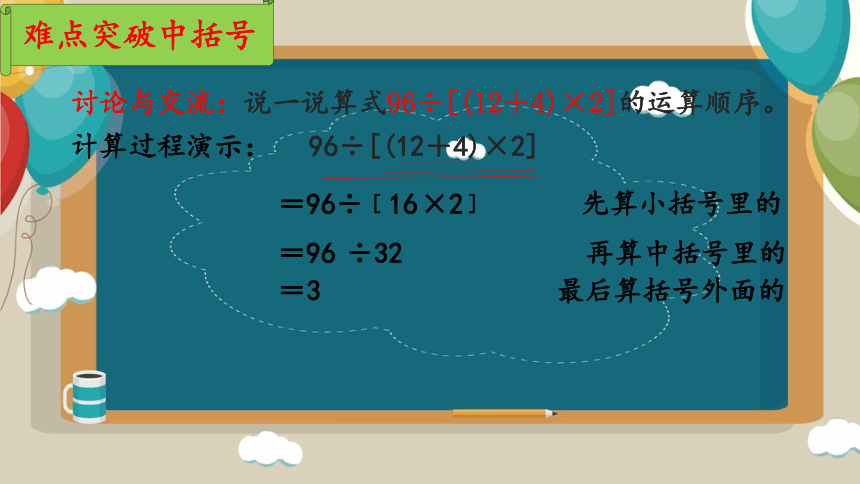
难点突破中括号
[ ]
16
先算小括号里的
再算中括号里的
最后算括号外面的
讨论与交流:说一说算式96÷[(12+4)×2]的运算顺序。
计算过程演示:
×2
÷32
运算顺序对比
合作与交流:比较以下三道算式的计算过程,找出它们在运算顺序上的区别。
③96÷[(12+4)×2]
=96÷[16×2]
=96÷32
=3
①96÷12+4×2
= 8+8
= 16
②96÷(12+4)×2
=96÷16×2
=6×2
=12
①在没有括号的算式里,如果既有加减法又有乘除法,要先算乘除法,再算加减法。同级运算从左往右依次计算。
②一个算式里,有小括号,要先算小括号里面的,再算括号外面的。
③一个算式里既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算括号外面的。
(1)计算3600÷60-30+10时,先算( )法,再算( )法,最后算( )法,计算结果是( )。
(2)计算3600÷(60-30)+10时,先算( )法,再算( )法,最后算( )法,计算结果是( )。
(3)计算3600÷[60-(30+10)]时,先算( )法,再算( )法,最后算( )法,计算结果是( )。
除
减
加
40
加
加
除
除
减
减
180
130
达标训练
填空我最棒!
÷
18 2 3 6 =
[ ]
添上适当的数学符号,使等式成立
1
×
( )
+
①
②
③
÷
18 2 3 6 =
[ ]
中括号和小括号都存在的时候,要先算小括号里的,再算中括号里的。
添上适当的数学符号,使等式成立
1
×
( )
+
中括号是怎么产生的?
谈谈对[ ]中括号的感受
“你的作用真大呀!”
“谢谢你,又帮我们解决了一个难题。”
“下次我再要改变运算顺序的时候就找你来帮忙。”
“数学符号家族里有你的加入,一定会更加有趣的。”
括号的产生
小括号“( )”公元17世纪由荷兰人吉拉特首先使用。
中括号“[ ]”公元17世纪英国数学家瓦里士最先使用。
大括号“{ }”法国数学家韦达在1593年首先使用。
1629年,荷兰基拉德采用了全部括号,18世纪开始世界通用。
巩固新知
填一填
2、计算(168-144)÷12×8时,要先算( )法,再算( )法,最后算( )法。
3、计算32×[(6+24)÷3]时,要先算( )法,再算( )法,最后算( )法。
1、在有括号的算式里,要先算( )括号里面的,再算( )括号里面的。
小
中
减
除
乘
加
除
乘
巩固新知
辩一辩
2、645-189×2 的计算结果是912。 ( )
1、30+60÷60-30 与(30+60)÷( 60 -30 ),的运算顺序和结果都是一样的。 ( )
3、4000与20的商减去15与24的和正确列式是4000÷20-( 15+274 )。 ( )
√
×
×
按照顺序计算,并填写下面的 ,然后列出综合算式。
275
6
275
11
3520
926
31484
320×[(128+147)÷25]=3520
(920+438÷73)×34=31484
巩固新知
课堂小结
这节课的学习中
(1)你新认识的数学符号是什么
(2)中括号、小括号在四则运算中有什么作用
(3)怎样计算含有中括号的混合运算
四则运算—括号
说一说下面算式的运算顺序。
A组 35-23+18 75+40-26
B组 34×15÷20 63÷9×24
C组 46-18×5 56÷8+5
D组 12×24-32÷8 63÷21+12×6
课前热身
观察A、B、C、D四组算式,你发现每组两个算式的运算顺序有什么共同的特点?
先乘除后加减、只有加减或者乘除的时候,从左往右依次计算,这些都是四则混合运算当中的法则。
四则混合运算
通常把4种运算统称为:
感受括号的作用
感受小括号的作用
2. 如果变成96÷(12+4)×2,运算顺序怎样?
3. 先说一说运算的顺序,再计算。
96÷12+4×2
问题:1. 说一说这道题的运算顺序是什么。
要先算小括号里面的。
预设:96÷(12+4)×2
=96÷16×2
=6×2
=12
思考与交流:如果想改变96÷ (12+4)×2 的运算顺序:先算加法,再算乘法,最后算除法,应该怎么办?
引入中括号
个算式用了小括号后,还需要改变运算顺序,就要使用中括号。
96÷[(12+4)×2]
( )
符号“[ ]”是中括号。它的作用与小括号一样,也是改变
混合运算的运算顺序,中括号要用在小括号的外面。当一
96÷[(12+4)×2]
=96÷
=96
=3
难点突破中括号
[ ]
16
先算小括号里的
再算中括号里的
最后算括号外面的
讨论与交流:说一说算式96÷[(12+4)×2]的运算顺序。
计算过程演示:
×2
÷32
运算顺序对比
合作与交流:比较以下三道算式的计算过程,找出它们在运算顺序上的区别。
③96÷[(12+4)×2]
=96÷[16×2]
=96÷32
=3
①96÷12+4×2
= 8+8
= 16
②96÷(12+4)×2
=96÷16×2
=6×2
=12
①在没有括号的算式里,如果既有加减法又有乘除法,要先算乘除法,再算加减法。同级运算从左往右依次计算。
②一个算式里,有小括号,要先算小括号里面的,再算括号外面的。
③一个算式里既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算括号外面的。
(1)计算3600÷60-30+10时,先算( )法,再算( )法,最后算( )法,计算结果是( )。
(2)计算3600÷(60-30)+10时,先算( )法,再算( )法,最后算( )法,计算结果是( )。
(3)计算3600÷[60-(30+10)]时,先算( )法,再算( )法,最后算( )法,计算结果是( )。
除
减
加
40
加
加
除
除
减
减
180
130
达标训练
填空我最棒!
÷
18 2 3 6 =
[ ]
添上适当的数学符号,使等式成立
1
×
( )
+
①
②
③
÷
18 2 3 6 =
[ ]
中括号和小括号都存在的时候,要先算小括号里的,再算中括号里的。
添上适当的数学符号,使等式成立
1
×
( )
+
中括号是怎么产生的?
谈谈对[ ]中括号的感受
“你的作用真大呀!”
“谢谢你,又帮我们解决了一个难题。”
“下次我再要改变运算顺序的时候就找你来帮忙。”
“数学符号家族里有你的加入,一定会更加有趣的。”
括号的产生
小括号“( )”公元17世纪由荷兰人吉拉特首先使用。
中括号“[ ]”公元17世纪英国数学家瓦里士最先使用。
大括号“{ }”法国数学家韦达在1593年首先使用。
1629年,荷兰基拉德采用了全部括号,18世纪开始世界通用。
巩固新知
填一填
2、计算(168-144)÷12×8时,要先算( )法,再算( )法,最后算( )法。
3、计算32×[(6+24)÷3]时,要先算( )法,再算( )法,最后算( )法。
1、在有括号的算式里,要先算( )括号里面的,再算( )括号里面的。
小
中
减
除
乘
加
除
乘
巩固新知
辩一辩
2、645-189×2 的计算结果是912。 ( )
1、30+60÷60-30 与(30+60)÷( 60 -30 ),的运算顺序和结果都是一样的。 ( )
3、4000与20的商减去15与24的和正确列式是4000÷20-( 15+274 )。 ( )
√
×
×
按照顺序计算,并填写下面的 ,然后列出综合算式。
275
6
275
11
3520
926
31484
320×[(128+147)÷25]=3520
(920+438÷73)×34=31484
巩固新知
课堂小结
这节课的学习中
(1)你新认识的数学符号是什么
(2)中括号、小括号在四则运算中有什么作用
(3)怎样计算含有中括号的混合运算
