北师大版八年级数学上册 1.3 勾股定理的应用最短路径问题同步练习(含答案)
文档属性
| 名称 | 北师大版八年级数学上册 1.3 勾股定理的应用最短路径问题同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 563.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 16:33:06 | ||
图片预览


文档简介
1.3 勾股定理的应用---最短路径问题
一、单选题
1.将一根的筷子,置于底面直径为,高的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度,则的取值范围是( )
A. B. C. D.
2.如图,底面周长为12,高为8的圆柱体上有一只小蚂蚁要从点A爬到点B,则蚂蚁爬行的最短距离是( )
A. B.8 C.10 D.12
3.如图,牧童家在B处,A、B两处相距河岸的距离AC、BD分别为500m和300m,且C、D两处的距离为600m,天黑牧童从A处将牛牵到河边去饮水,在赶回家,那么牧童最少要走( )
A.800m B.1000m C.1200m D.1500m
4.如图所示,有一根高为的木柱,它的底面周长为,在准备元旦联欢晚会时,为了营造喜庆的气氛,老师要求小明将一根彩带从底柱向柱顶均匀地缠绕7圈,一直缠到起点的正上方为止,小明需要准备的这根彩带的长至少为( ).
A. B. C. D.
5.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
6.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为的半圆,其边缘.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )m.(取3)
A.30 B.28 C.25 D.22
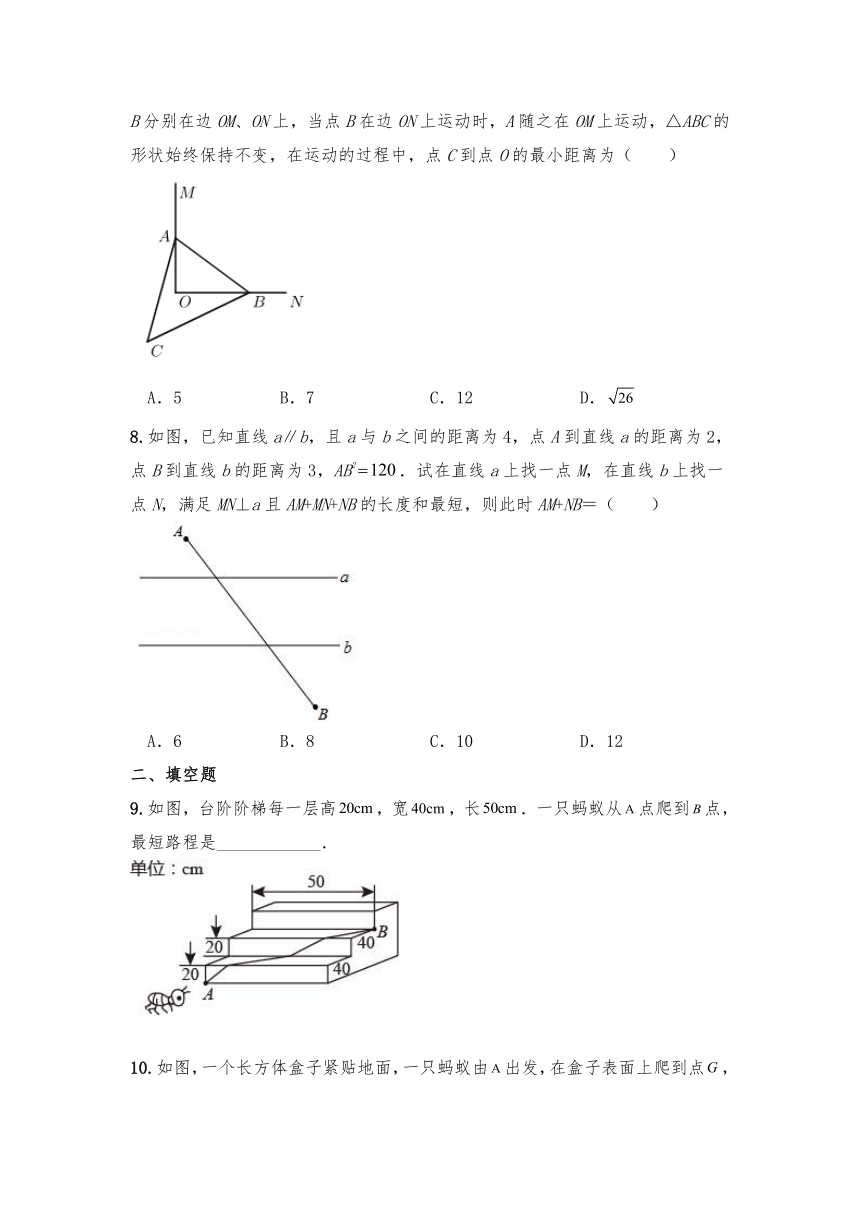
7.如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为( )
A.5 B.7 C.12 D.
8.如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB2.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
A.6 B.8 C.10 D.12
二、填空题
9.如图,台阶阶梯每一层高,宽,长.一只蚂蚁从点爬到点,最短路程是____________.
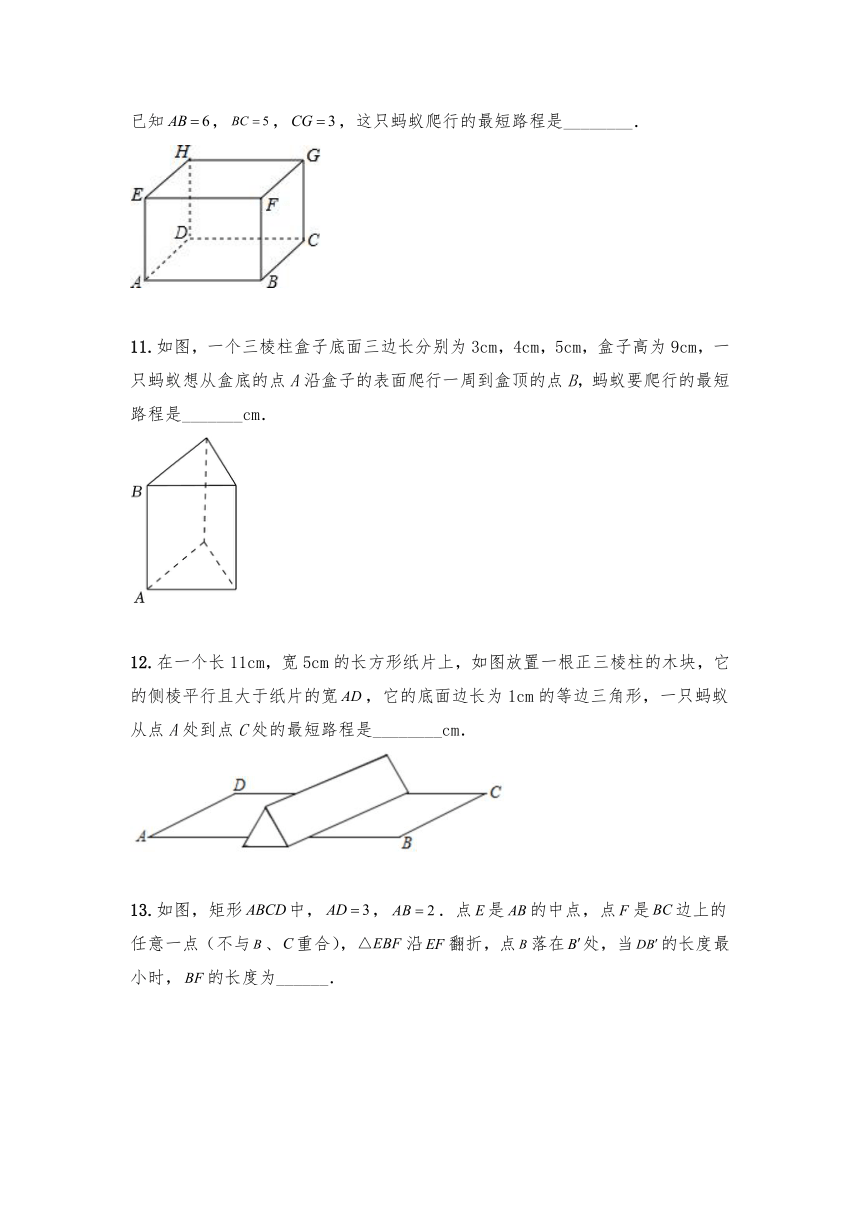
10.如图,一个长方体盒子紧贴地面,一只蚂蚁由出发,在盒子表面上爬到点,已知,,,这只蚂蚁爬行的最短路程是________.
11.如图,一个三棱柱盒子底面三边长分别为3cm,4cm,5cm,盒子高为9cm,一只蚂蚁想从盒底的点A沿盒子的表面爬行一周到盒顶的点B,蚂蚁要爬行的最短路程是_______cm.
12.在一个长11cm,宽5cm的长方形纸片上,如图放置一根正三棱柱的木块,它的侧棱平行且大于纸片的宽,它的底面边长为1cm的等边三角形,一只蚂蚁从点A处到点C处的最短路程是________cm.
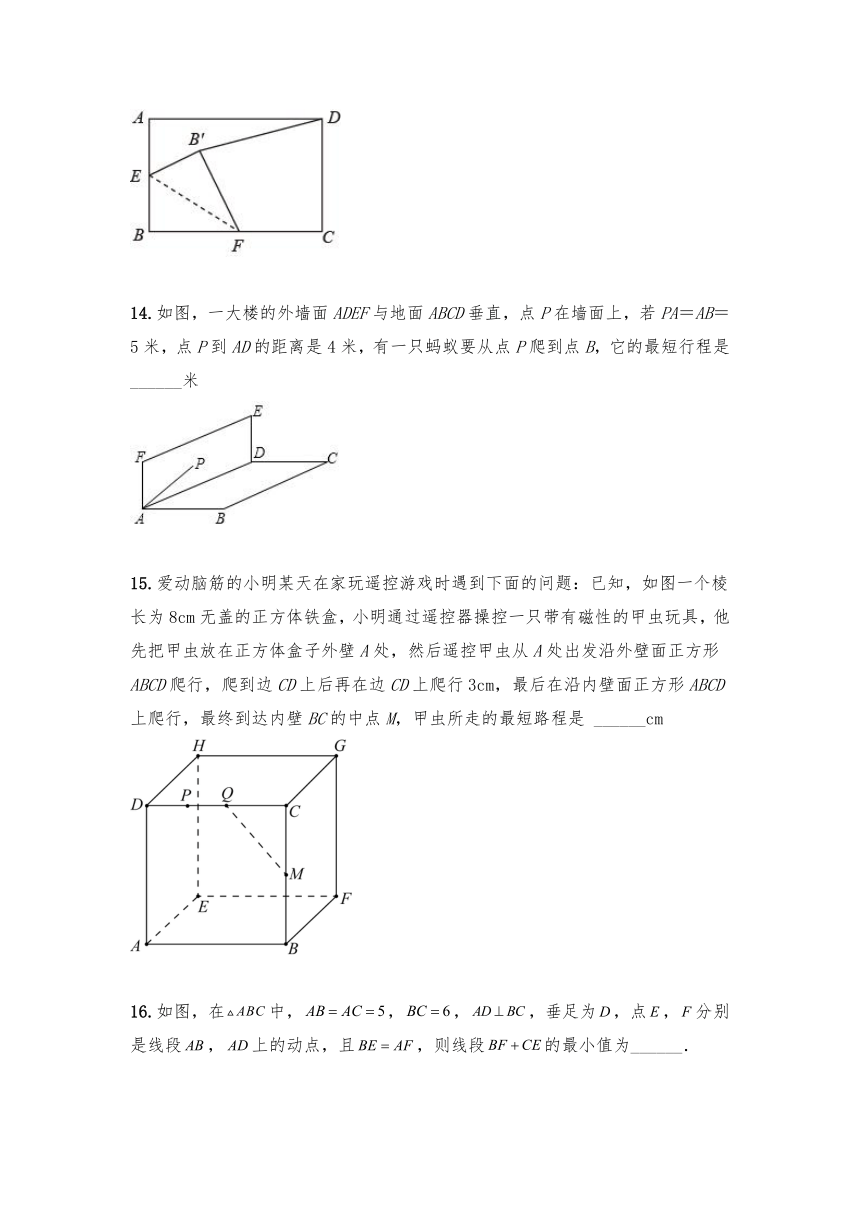
13.如图,矩形中,,.点是的中点,点是边上的任意一点(不与、重合),沿翻折,点落在处,当的长度最小时,的长度为______.
14.如图,一大楼的外墙面ADEF与地面ABCD垂直,点P在墙面上,若PA=AB=5米,点P到AD的距离是4米,有一只蚂蚁要从点P爬到点B,它的最短行程是______米
15.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是 ______cm
16.如图,在中,,,,垂足为,点,分别是线段,上的动点,且,则线段的最小值为______.
三、解答题
17.如图,小明家在一条东西走向的公路北侧米的点处,小红家位于小明家北米(米)、东米(米)点处.
(1)求小明家离小红家的距离;(2)现要在公路上的点处建一个快递驿站,使最小,请确定点的位置,并求的最小值.
18.如图,在四边形ABCD形状的池塘上,要从C处出发,架设一座小桥CP连接对岸AD,已知AB=BC=6米,AB⊥BC,∠A=105°且∠BCD=135°,求小桥CP长度的最小值.
19.有一个如图所示的长方体透明玻璃水缸,高,水深,在水面线上紧贴内壁处有一粒食物,且,一只小虫想从水缸外的处沿水缸壁爬到水缸内的处吃掉食物.(1)你认为小虫应该沿怎样的路线爬行才能使爬行的路线最短,请你画出它爬行的最短路线,并用箭头标注.(2)求小虫爬行的最短路线长(不计缸壁厚度).
20.如图,在公路的同侧有两个居民点、,居民点、分别到公路的距离千米和千米,且两个居民点、相距千米.
(1)要在公路边修一个污水处理站来收集处理居民点、的污水,污水处理站修在什么地方到居民点、所用的水管最短;请你在图中设计出污水处理站的位置.(保留作图痕迹,不要证明)
(2)如图铺设水管的工程费用为每千米万元,为使铺设水管的费用最节省,请求出最节省的费用为多少万元?(3)要在公路边修一个汽车站,使汽车站到两个居民点、的距离相等,则点应该修在距点多远的地方(另画图并写出解答过程)
21.(1)如图1,长方体的底面边长分别为3m和2m,高为1m,在盒子里,可以放入最长为_______m的木棒;(2)如图2,在与(1)相同的长方体中,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点C,那么所用细线最短需要______m;(3)如图3,长方体的棱长分别为AB=BC=6cm,假设昆虫甲从盒内顶点以2厘米/秒的速度在盒子的内部沿棱向下爬行,同时昆虫乙从盒内顶点A以相同的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉昆虫甲
22.早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.
如图2,作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是所求的位置.
证明:如图3,在直线l上另取任一点C′,连结AC′,BC′,B′C′,
∵直线l是点B,B′的对称轴,点C,C′在l上,∴CB=CB′,C′B=C′B′,
∴AC+CB=AC+ = .
在△AC′B′中,∵AB′<AC′+C′B′∴AC+CB<AC′+C′B′即AC+CB最小.
本问题实际上是利用轴对称变换的思想,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A、C、B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.
1.简单应用(1)如图4,在等边△ABC中,AB=6,AD⊥BC,E是AC的中点,M是AD上的一点,求EM+MC的最小值
借助上面的模型,由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,EM+MC的最小值就是线段 的长度,则EM+MC的最小值是 ;
(2)如图5,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M、N当△AMN周长最小时,∠AMN+∠ANM= °.
2.拓展应用:如图6,是一个港湾,港湾两岸有A、B两个码头,∠AOB=30°,OA=1千米,OB=2千米,现有一艘货船从码头A出发,根据计划,货船应先停靠OB岸C处装货,再停靠OA岸D处装货,最后到达码头B.怎样安排两岸的装货地点,使货船行驶的水路最短?请画出最短路线并求出最短路程.
答案
一、单选题
D.C.B.B.B.C.B.B.
二、填空题
9.
10.
11.15
12.13
13.
14.
15.16
16.
三、解答题
17.解:(1)如图,连接AB,
由题意知AC=500,BC=1200,∠ACB=90°,
在Rt△ABC中,∵∠ACB=90°,∴AB2=AC2+BC2=5002+12002=1690000,
∵AB>0∴AB=1300米;
(2)如图,作点A关于直线MN的对称点A',连接A'B交MN于点P.
驿站到小明家和到小红家距离和的最小值即为A'B,
由题意知AD=200米,A'C⊥MN,∴A'C=AC+AD+A'D=500+200+200=900米,
在Rt△A'BC中,∵∠ACB=90°,∴A'B2=A'C2+BC2=9002+12002=2250000,
∵A'B>0,∴A'B=1500米,即从驿站到小明家和到小红家距离和的最小值为1500米.
18.解:当CP⊥AD时,CP的长度最小, 如图,连接AC,
∵AB=BC,∠B=90°,∴∠BAC=45°,∴∠PAC=∠BAP﹣∠BAC=105°﹣45°=60°,
∵CP⊥AD,∴∠PCA=30°,在Rt△ABC中,AB=BC=6米,∴AC==6(米),
在Rt△APC中,AP=AC=3(米),∴CP=(米).
答:小桥CP长度的最小值为3米.
19.解:(1)如下图所示,
作点A关于BC所在直线的对称点,连接,与交于点,
由两点之间线段最短,此时A’G最短,则为最短路线.
(2)∵,∴,∴.
在中,,,∴.
由对称性可知,∴.故小虫爬行的最短路线长为100cm.
20.(1)如图1所示,点即为所求.
(2)如图1,过点作于点,过点作,交延长线于点,
则四边形和四边形均为矩形,
,,则,,
在中,,,
则,所以最节省的费用为(万元).
(3)如图,作的中垂线,交于点,则点即为所求;
连接、,设,则,
,,即,
解得:,即点在距离点的地方.
21.(1)最长的为斜对角线:=;
(2)这根细线的长为:=;
(3)设昆虫甲从顶点沿棱向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F,爬行捕捉到昆虫甲需x秒钟,如图1在Rt△ACF中, ∵x>0,解得:
答:昆虫乙至少需要秒钟才能捕捉到昆虫甲.
22.解:AC+CB=AC+C′B=AB′,故答案为:C′B;AB′;
1.简单应用(1)由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,
EM+MC的最小值就是线段BE的长度,BE=,
则EM+MC的最小值是,故答案为:BE;;
(2)如图5,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,
则A′A″即为△AMN的周长最小值,∵∠DAB=130°,∴∠A′+∠A″=50°,
∵∠A′=∠MAA′,∠NAD=∠A″,且∠A′+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAD+∠A″=2(∠A′+∠A″)=2×50°=100°,故答案为:100;
2.拓展应用:如图6,分别作点A关于OB的对称点A′,点B关于OA的对称点B′,连接A′B′,交OB于C,交OA于D,则C、D为两岸的装货地点,A′B′是货船行驶的水路最短路程,
由轴对称的性质可知,OA′=OA=1,OB′=OB=2,∠BOA′=∠AOB=30°,∠AOB′=∠AOB=30°,
∴∠A′OB′=90°,∴A′B′=,答:货船行驶的水路最短路程为千米.
一、单选题
1.将一根的筷子,置于底面直径为,高的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度,则的取值范围是( )
A. B. C. D.
2.如图,底面周长为12,高为8的圆柱体上有一只小蚂蚁要从点A爬到点B,则蚂蚁爬行的最短距离是( )
A. B.8 C.10 D.12
3.如图,牧童家在B处,A、B两处相距河岸的距离AC、BD分别为500m和300m,且C、D两处的距离为600m,天黑牧童从A处将牛牵到河边去饮水,在赶回家,那么牧童最少要走( )
A.800m B.1000m C.1200m D.1500m
4.如图所示,有一根高为的木柱,它的底面周长为,在准备元旦联欢晚会时,为了营造喜庆的气氛,老师要求小明将一根彩带从底柱向柱顶均匀地缠绕7圈,一直缠到起点的正上方为止,小明需要准备的这根彩带的长至少为( ).
A. B. C. D.
5.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
6.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为的半圆,其边缘.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )m.(取3)
A.30 B.28 C.25 D.22
7.如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为( )
A.5 B.7 C.12 D.
8.如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB2.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
A.6 B.8 C.10 D.12
二、填空题
9.如图,台阶阶梯每一层高,宽,长.一只蚂蚁从点爬到点,最短路程是____________.
10.如图,一个长方体盒子紧贴地面,一只蚂蚁由出发,在盒子表面上爬到点,已知,,,这只蚂蚁爬行的最短路程是________.
11.如图,一个三棱柱盒子底面三边长分别为3cm,4cm,5cm,盒子高为9cm,一只蚂蚁想从盒底的点A沿盒子的表面爬行一周到盒顶的点B,蚂蚁要爬行的最短路程是_______cm.
12.在一个长11cm,宽5cm的长方形纸片上,如图放置一根正三棱柱的木块,它的侧棱平行且大于纸片的宽,它的底面边长为1cm的等边三角形,一只蚂蚁从点A处到点C处的最短路程是________cm.
13.如图,矩形中,,.点是的中点,点是边上的任意一点(不与、重合),沿翻折,点落在处,当的长度最小时,的长度为______.
14.如图,一大楼的外墙面ADEF与地面ABCD垂直,点P在墙面上,若PA=AB=5米,点P到AD的距离是4米,有一只蚂蚁要从点P爬到点B,它的最短行程是______米
15.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是 ______cm
16.如图,在中,,,,垂足为,点,分别是线段,上的动点,且,则线段的最小值为______.
三、解答题
17.如图,小明家在一条东西走向的公路北侧米的点处,小红家位于小明家北米(米)、东米(米)点处.
(1)求小明家离小红家的距离;(2)现要在公路上的点处建一个快递驿站,使最小,请确定点的位置,并求的最小值.
18.如图,在四边形ABCD形状的池塘上,要从C处出发,架设一座小桥CP连接对岸AD,已知AB=BC=6米,AB⊥BC,∠A=105°且∠BCD=135°,求小桥CP长度的最小值.
19.有一个如图所示的长方体透明玻璃水缸,高,水深,在水面线上紧贴内壁处有一粒食物,且,一只小虫想从水缸外的处沿水缸壁爬到水缸内的处吃掉食物.(1)你认为小虫应该沿怎样的路线爬行才能使爬行的路线最短,请你画出它爬行的最短路线,并用箭头标注.(2)求小虫爬行的最短路线长(不计缸壁厚度).
20.如图,在公路的同侧有两个居民点、,居民点、分别到公路的距离千米和千米,且两个居民点、相距千米.
(1)要在公路边修一个污水处理站来收集处理居民点、的污水,污水处理站修在什么地方到居民点、所用的水管最短;请你在图中设计出污水处理站的位置.(保留作图痕迹,不要证明)
(2)如图铺设水管的工程费用为每千米万元,为使铺设水管的费用最节省,请求出最节省的费用为多少万元?(3)要在公路边修一个汽车站,使汽车站到两个居民点、的距离相等,则点应该修在距点多远的地方(另画图并写出解答过程)
21.(1)如图1,长方体的底面边长分别为3m和2m,高为1m,在盒子里,可以放入最长为_______m的木棒;(2)如图2,在与(1)相同的长方体中,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点C,那么所用细线最短需要______m;(3)如图3,长方体的棱长分别为AB=BC=6cm,假设昆虫甲从盒内顶点以2厘米/秒的速度在盒子的内部沿棱向下爬行,同时昆虫乙从盒内顶点A以相同的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉昆虫甲
22.早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.
如图2,作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是所求的位置.
证明:如图3,在直线l上另取任一点C′,连结AC′,BC′,B′C′,
∵直线l是点B,B′的对称轴,点C,C′在l上,∴CB=CB′,C′B=C′B′,
∴AC+CB=AC+ = .
在△AC′B′中,∵AB′<AC′+C′B′∴AC+CB<AC′+C′B′即AC+CB最小.
本问题实际上是利用轴对称变换的思想,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A、C、B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.
1.简单应用(1)如图4,在等边△ABC中,AB=6,AD⊥BC,E是AC的中点,M是AD上的一点,求EM+MC的最小值
借助上面的模型,由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,EM+MC的最小值就是线段 的长度,则EM+MC的最小值是 ;
(2)如图5,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M、N当△AMN周长最小时,∠AMN+∠ANM= °.
2.拓展应用:如图6,是一个港湾,港湾两岸有A、B两个码头,∠AOB=30°,OA=1千米,OB=2千米,现有一艘货船从码头A出发,根据计划,货船应先停靠OB岸C处装货,再停靠OA岸D处装货,最后到达码头B.怎样安排两岸的装货地点,使货船行驶的水路最短?请画出最短路线并求出最短路程.
答案
一、单选题
D.C.B.B.B.C.B.B.
二、填空题
9.
10.
11.15
12.13
13.
14.
15.16
16.
三、解答题
17.解:(1)如图,连接AB,
由题意知AC=500,BC=1200,∠ACB=90°,
在Rt△ABC中,∵∠ACB=90°,∴AB2=AC2+BC2=5002+12002=1690000,
∵AB>0∴AB=1300米;
(2)如图,作点A关于直线MN的对称点A',连接A'B交MN于点P.
驿站到小明家和到小红家距离和的最小值即为A'B,
由题意知AD=200米,A'C⊥MN,∴A'C=AC+AD+A'D=500+200+200=900米,
在Rt△A'BC中,∵∠ACB=90°,∴A'B2=A'C2+BC2=9002+12002=2250000,
∵A'B>0,∴A'B=1500米,即从驿站到小明家和到小红家距离和的最小值为1500米.
18.解:当CP⊥AD时,CP的长度最小, 如图,连接AC,
∵AB=BC,∠B=90°,∴∠BAC=45°,∴∠PAC=∠BAP﹣∠BAC=105°﹣45°=60°,
∵CP⊥AD,∴∠PCA=30°,在Rt△ABC中,AB=BC=6米,∴AC==6(米),
在Rt△APC中,AP=AC=3(米),∴CP=(米).
答:小桥CP长度的最小值为3米.
19.解:(1)如下图所示,
作点A关于BC所在直线的对称点,连接,与交于点,
由两点之间线段最短,此时A’G最短,则为最短路线.
(2)∵,∴,∴.
在中,,,∴.
由对称性可知,∴.故小虫爬行的最短路线长为100cm.
20.(1)如图1所示,点即为所求.
(2)如图1,过点作于点,过点作,交延长线于点,
则四边形和四边形均为矩形,
,,则,,
在中,,,
则,所以最节省的费用为(万元).
(3)如图,作的中垂线,交于点,则点即为所求;
连接、,设,则,
,,即,
解得:,即点在距离点的地方.
21.(1)最长的为斜对角线:=;
(2)这根细线的长为:=;
(3)设昆虫甲从顶点沿棱向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F,爬行捕捉到昆虫甲需x秒钟,如图1在Rt△ACF中, ∵x>0,解得:
答:昆虫乙至少需要秒钟才能捕捉到昆虫甲.
22.解:AC+CB=AC+C′B=AB′,故答案为:C′B;AB′;
1.简单应用(1)由等边三角形的轴对称性可知,B与C关于直线AD对称,连结BM,
EM+MC的最小值就是线段BE的长度,BE=,
则EM+MC的最小值是,故答案为:BE;;
(2)如图5,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,
则A′A″即为△AMN的周长最小值,∵∠DAB=130°,∴∠A′+∠A″=50°,
∵∠A′=∠MAA′,∠NAD=∠A″,且∠A′+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAD+∠A″=2(∠A′+∠A″)=2×50°=100°,故答案为:100;
2.拓展应用:如图6,分别作点A关于OB的对称点A′,点B关于OA的对称点B′,连接A′B′,交OB于C,交OA于D,则C、D为两岸的装货地点,A′B′是货船行驶的水路最短路程,
由轴对称的性质可知,OA′=OA=1,OB′=OB=2,∠BOA′=∠AOB=30°,∠AOB′=∠AOB=30°,
∴∠A′OB′=90°,∴A′B′=,答:货船行驶的水路最短路程为千米.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
