3.2.1双曲线及其标准方程 课件(共15张PPT)
文档属性
| 名称 | 3.2.1双曲线及其标准方程 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 12:21:43 | ||
图片预览






文档简介
(共15张PPT)
3.2.1
双曲线及其标准方程
人教A版(2019)选择性必修第一册
学习目标
1. 掌握双曲线的定义及其标准方程的推导过程。
2. 运用解析法(坐标法)研究双曲线的标准方程,并能利用其解决相关问题。
3. 核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
椭圆的概念及其标准方程
定义:我们把平面内与两个定点, 的距离的和等于常数(大于||)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间距离叫做椭圆的焦距,焦距的一半称为半焦距.
椭圆的标准方程:①焦点在:1 (0).
②焦点在:1 (0).
二、新课讲授
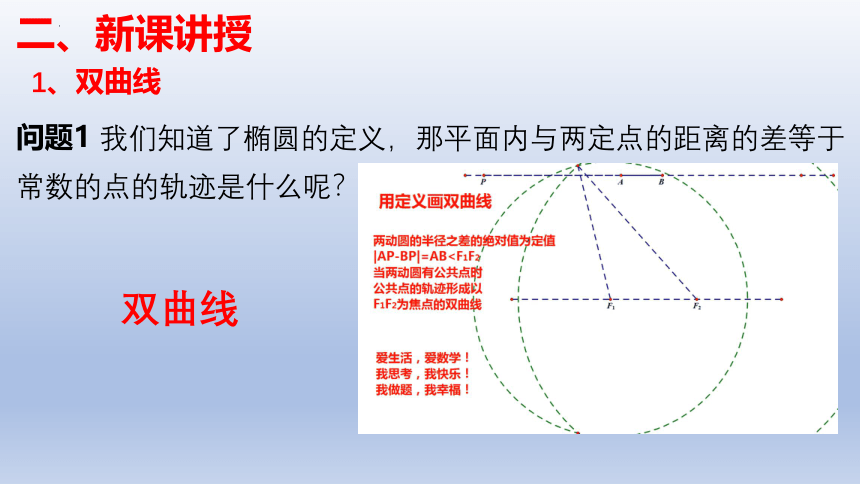
1、双曲线
问题1 我们知道了椭圆的定义,那平面内与两定点的距离的差等于常数的点的轨迹是什么呢?
双曲线
问题2 你能类比椭圆的定义给出双曲线的定义吗?
定义:一般地,我们把平面内与两个定点, 的距离的差的绝对值等于非零常数(小于||)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间距离叫做双曲线的焦距.
追问1 “差的绝对值”把“绝对值”去掉可以吗,此时的轨迹是什么?
分析:当平面内与两个定点, 的距离的差等于非零常数(小于||)时,点的轨迹是双曲线的一支.
差是大于0的常数时,轨迹是双曲线右支
差是小于0的常数时,轨迹是双曲线左支
追问2 “小于||”改为“等于||” 可以吗,此时的轨迹是什么?改为“大于”呢?
分析:“等于||”时轨迹是一条射线;“大于||”时,轨迹不存在.
追问3 “非零常数”去掉“非零” 可以吗?
分析:当平面内与两个定点, 的距离的差等于0时,点的轨迹是线段的中垂线.
2、双曲线的标准方程
问题3 你能类比椭圆标准方程的推导过程推导出双曲线的标准方程?
建系→设点→列式→化简→检验
建系:以经过双曲线两焦点的直线为轴,线段的垂直平分线为轴,建立直角坐标系.
1、建立适当的坐标系,用有序数对()表示曲线上的任意一点的坐标;
2、写出合适条件的点的集合是建立曲线方程的依据;
3、用坐标表示条件,列出方程0,这是建立曲线方程是关键;
4、将方程0化为最简形式,以化简后的方程的解为坐标的点都在曲线上,反之也成立.
问题4 如何用坐标表示双曲线上的点所满足的条件?
分析:由双曲线的定义可知,双曲线可看作点集:
设是双曲线上任意一点,双曲线的焦距为,那么焦点, 的坐标分别为, .
由有
类比椭圆,化简得 ()
上式同除以得到1(0).
令 ,
则上式变形为 ,
因为方程 变形到1 (0)的过程中都是同解变形,所以双曲线上任意一点的坐标都满足该方程;反之,以方程1 (0)的解为坐标的点都在双曲线上.
我们称方程1 (0)是双曲线的标准方程,它表示焦点在轴上,两焦点分别是 , 的双曲线,这里
.
追问1 1 (0)是双曲线的标准方程吗?
分析:1 (0)是双曲线的标准方程,它表示焦点在轴上,两焦点分别是 , 的双曲线.
双曲线的标准方程:①焦点在: 1 (0).
②焦点在: 1 (0).
三、巩固新知
例1 设双曲线的两个焦点坐标分别为 , ,双曲线上一点与 ,的距离差的绝对值等于6 ,求双曲线的标准方程.
解:因为双曲线的焦点在轴上,所以设它的标准方程为1 (0).
由10, 6,得5, 3,
则 9=16.
所求双曲线的标准方程为 1.
例2 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
解:如图所示,建立直角坐标系, 使A、B两点在轴上,并且点O与线段AB的中点重合.
由题意可知, ,所以,点轨迹是以为焦点的双曲线的右支.
所以=680,则=340, =115600,
=800,则=400,则 =44400,
所以炮弹爆炸点的轨迹方程为 1( ≥340).
四、课堂小结
1、双曲线的概念及其标准方程
五、作业布置
课本P121:练习 第3、4题
椭圆及其标准方程 双曲线及其标准方程
0, 0,
焦点在1 (0) 焦点在1 (0) 焦点在1 (0) 焦点在 1 (0)
3.2.1
双曲线及其标准方程
人教A版(2019)选择性必修第一册
学习目标
1. 掌握双曲线的定义及其标准方程的推导过程。
2. 运用解析法(坐标法)研究双曲线的标准方程,并能利用其解决相关问题。
3. 核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
椭圆的概念及其标准方程
定义:我们把平面内与两个定点, 的距离的和等于常数(大于||)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间距离叫做椭圆的焦距,焦距的一半称为半焦距.
椭圆的标准方程:①焦点在:1 (0).
②焦点在:1 (0).
二、新课讲授
1、双曲线
问题1 我们知道了椭圆的定义,那平面内与两定点的距离的差等于常数的点的轨迹是什么呢?
双曲线
问题2 你能类比椭圆的定义给出双曲线的定义吗?
定义:一般地,我们把平面内与两个定点, 的距离的差的绝对值等于非零常数(小于||)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间距离叫做双曲线的焦距.
追问1 “差的绝对值”把“绝对值”去掉可以吗,此时的轨迹是什么?
分析:当平面内与两个定点, 的距离的差等于非零常数(小于||)时,点的轨迹是双曲线的一支.
差是大于0的常数时,轨迹是双曲线右支
差是小于0的常数时,轨迹是双曲线左支
追问2 “小于||”改为“等于||” 可以吗,此时的轨迹是什么?改为“大于”呢?
分析:“等于||”时轨迹是一条射线;“大于||”时,轨迹不存在.
追问3 “非零常数”去掉“非零” 可以吗?
分析:当平面内与两个定点, 的距离的差等于0时,点的轨迹是线段的中垂线.
2、双曲线的标准方程
问题3 你能类比椭圆标准方程的推导过程推导出双曲线的标准方程?
建系→设点→列式→化简→检验
建系:以经过双曲线两焦点的直线为轴,线段的垂直平分线为轴,建立直角坐标系.
1、建立适当的坐标系,用有序数对()表示曲线上的任意一点的坐标;
2、写出合适条件的点的集合是建立曲线方程的依据;
3、用坐标表示条件,列出方程0,这是建立曲线方程是关键;
4、将方程0化为最简形式,以化简后的方程的解为坐标的点都在曲线上,反之也成立.
问题4 如何用坐标表示双曲线上的点所满足的条件?
分析:由双曲线的定义可知,双曲线可看作点集:
设是双曲线上任意一点,双曲线的焦距为,那么焦点, 的坐标分别为, .
由有
类比椭圆,化简得 ()
上式同除以得到1(0).
令 ,
则上式变形为 ,
因为方程 变形到1 (0)的过程中都是同解变形,所以双曲线上任意一点的坐标都满足该方程;反之,以方程1 (0)的解为坐标的点都在双曲线上.
我们称方程1 (0)是双曲线的标准方程,它表示焦点在轴上,两焦点分别是 , 的双曲线,这里
.
追问1 1 (0)是双曲线的标准方程吗?
分析:1 (0)是双曲线的标准方程,它表示焦点在轴上,两焦点分别是 , 的双曲线.
双曲线的标准方程:①焦点在: 1 (0).
②焦点在: 1 (0).
三、巩固新知
例1 设双曲线的两个焦点坐标分别为 , ,双曲线上一点与 ,的距离差的绝对值等于6 ,求双曲线的标准方程.
解:因为双曲线的焦点在轴上,所以设它的标准方程为1 (0).
由10, 6,得5, 3,
则 9=16.
所求双曲线的标准方程为 1.
例2 已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.
解:如图所示,建立直角坐标系, 使A、B两点在轴上,并且点O与线段AB的中点重合.
由题意可知, ,所以,点轨迹是以为焦点的双曲线的右支.
所以=680,则=340, =115600,
=800,则=400,则 =44400,
所以炮弹爆炸点的轨迹方程为 1( ≥340).
四、课堂小结
1、双曲线的概念及其标准方程
五、作业布置
课本P121:练习 第3、4题
椭圆及其标准方程 双曲线及其标准方程
0, 0,
焦点在1 (0) 焦点在1 (0) 焦点在1 (0) 焦点在 1 (0)
