2023年广西壮族自治区贵港市平南县中考模拟预测数学试题(含解析)
文档属性
| 名称 | 2023年广西壮族自治区贵港市平南县中考模拟预测数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 647.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 21:19:50 | ||
图片预览




文档简介
2023年广西壮族自治区贵港市平南县中考模拟预测数学试题
一、选择题(共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)
1.2023的相反数是( )
A. B. C.2023 D.﹣2023
2.随着我国航天领域的快速发展,从“天宫一号”发射升空,到天和核心舱归位,其图标既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.截至5月17日,南水北调东中线一期工程已累计向北方输水超6.2×1010立方米,直接受益人口超1.5亿人,其中6.2×1010立方米可表示为( )
A.6.2亿立方米 B.62亿立方米
C.620亿立方米 D.6200亿立方米
4.下列运算正确的是( )
A.a3+a2=a5 B.(a4)2=a8
C.a6÷a2=a3 D.﹣3(a﹣b)=﹣3a﹣3b
5.在直角坐标系中,点A的坐标为(2,﹣3),那么点A关于原点对称的点A1的坐标是( )
A.(﹣2,3) B.(﹣2,﹣3) C.(2,3) D.(﹣3,﹣2)
6.如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转( )
A.10° B.20° C.30° D.40°
7.若关于x的方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A.k>﹣1 B.k<﹣1 C.k≥﹣1且k≠0 D.k>﹣1且k≠0
8.下列事件中,是必然事件的是( )
A.疫情期间,对从疫情高风险区归来的人员进行核酸检测,检测结果为阳性
B.任意画一个三角形,其内角和为180°
C.某校开展“喜迎二十大,筑梦向未来”主题学习活动中,抽到A同学分享发言
D.打开电视机,正在播放“天宫课堂”
9.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,引绳度之,余绳四尺五寸,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余4.5尺;将绳子对折再量木头,问木头长多少尺?可设木头长为x尺,绳子长为y尺( )
A. B.
C. D.
10.如图,在5×4的网格图中,每个小正方形的边长均为1.设经过格点A,B,则弧AD的弧长为( )
A.π B.π C.π D.π
11.某天早晨7:00,小龚从家骑自行车去上学,途中因自行车发生故障,修好车后继续骑行,7:20赶到了学校,结合图象,判断下列结论正确的是( )
A.小龚修好车后骑行到学校的平均速度是3m/s
B.小龚家距离学校750m
C.小龚修好车后花了20分钟到达学校
D.小龚修车花了10分钟
12.如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,AE∥OB,反比例函数,若 OA=6,OC=4( )
A.6 B.11.25 C.12 D.18
二、填空题(本大题共6小题,每小题2分,共12分.)
13.(2分)化简= .
14.(2分)已知分式=0,则x= .
15.(2分)明珠塔楼是一栋古代工艺与现代精工艺完美融合的中式建筑.数学活动课上,老师带领兴趣小组去测量明珠塔的高度.如图,在C处用高0.5米的测倾器CE测得塔顶A的仰角为30°,在D处测得塔顶A的仰角为 60°,则明珠塔的高约为 米(结果保留根号).
16.(2分)有一组数据:3,a,4,6,7.它们的平均数是5,那么这组数据的方差是 .
17.(2分)在平面直角坐标系中,一次函数y=2x+3的图象与x轴的交点坐标是 .
18.(2分)如图,将半径为4,圆心角为90°的扇形ABC绕弧AC的中点P逆时针旋转 45°,B,C的对应点分别为点D,E,F,点D落在AB上,则图中阴影部分的面积为 .
三、解答题(本大题共8小题,满分72分,解答应写出文字说明、证明过程或演算步骤)
19.(6分)计算:(﹣3)2×3﹣1+(﹣8+5)+tan60°
20.(6分)先化简,再求值:
,其中x=﹣1,y=2.
21.(10分)如图,AB为⊙O的直径,点C在⊙O上.
(1)尺规作图(不写作法,保留作图痕迹):在⊙O上作点D,使得线段DB=DC,
且线段AD与BC相交;
(2)在(1)的条件下,AD与BC相交于点P,求∠ADC 的度数.
22.(10分)阅读理解学习
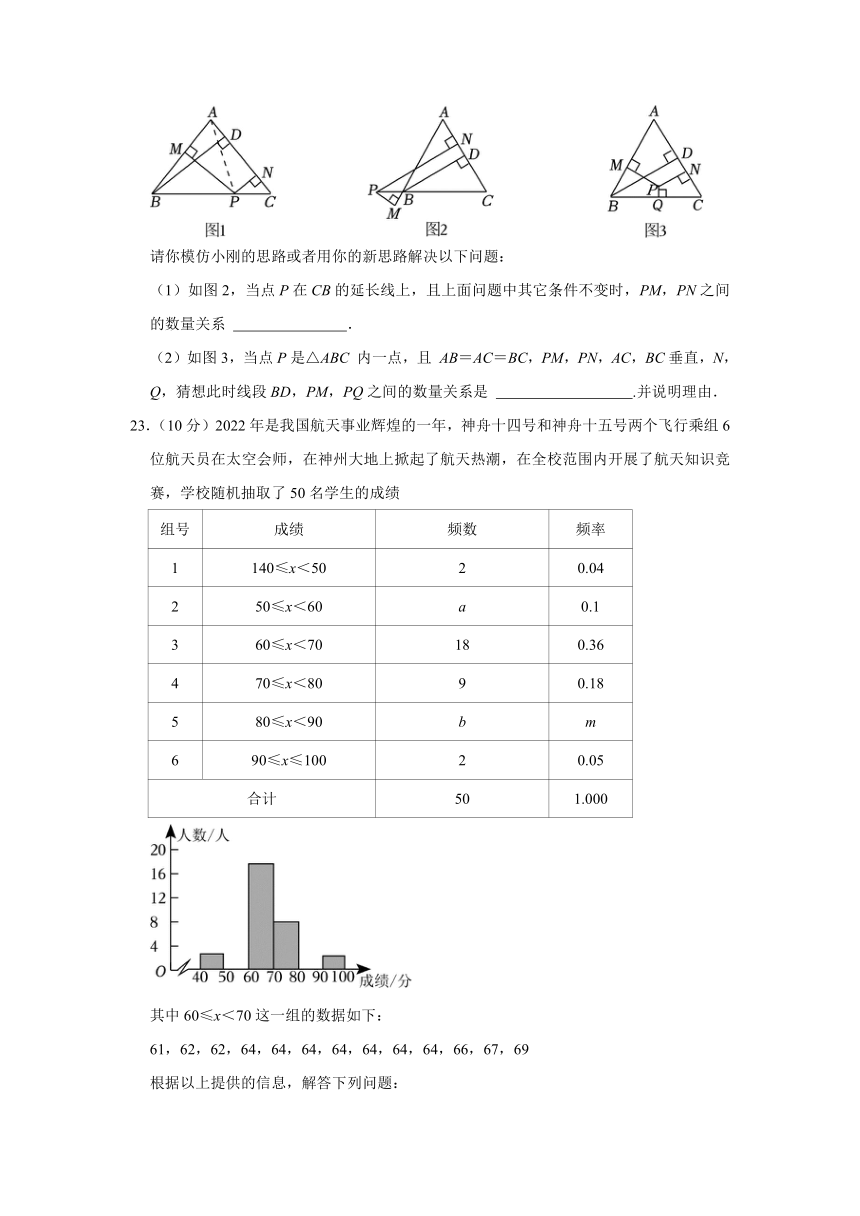
如图1,在△ABC中,AB=AC,P是BC边上一点,PM,AC垂直,垂足分别为M,N,有 S△ABC=S△ABP+S△ACP,即,由AB=AC 可得 BD=PM+PN.
请你模仿小刚的思路或者用你的新思路解决以下问题:
(1)如图2,当点P在CB的延长线上,且上面问题中其它条件不变时,PM,PN之间的数量关系 .
(2)如图3,当点P是△ABC 内一点,且 AB=AC=BC,PM,PN,AC,BC垂直,N,Q,猜想此时线段BD,PM,PQ之间的数量关系是 .并说明理由.
23.(10分)2022年是我国航天事业辉煌的一年,神舟十四号和神舟十五号两个飞行乘组6位航天员在太空会师,在神州大地上掀起了航天热潮,在全校范围内开展了航天知识竞赛,学校随机抽取了50名学生的成绩
组号 成绩 频数 频率
1 140≤x<50 2 0.04
2 50≤x<60 a 0.1
3 60≤x<70 18 0.36
4 70≤x<80 9 0.18
5 80≤x<90 b m
6 90≤x≤100 2 0.05
合计 50 1.000
其中60≤x<70这一组的数据如下:
61,62,62,64,64,64,64,64,64,64,66,67,69
根据以上提供的信息,解答下列问题:
(1)表格中a= ,b= ,m= ;
(2)60≤x<70这一组数据的众数是 ,中位数是 ;
(3)若以组中值(每组正中间数值)为本组数据的平均数,全校共有1500名学生参与竞赛
24.(10分)为实现“乡村振兴”战略目标,某乡镇制定了“以产业带动发展”的策略,开发出了某新型农产品,B两种型号的货车将该农产品运往外地销售,已知用1辆A型车和2辆B型车载满该农产品一次可运11吨,计划一次运完,且每辆车都满载.
(1)1辆A型货车和1辆B型货车满载时一次分别运该农产品多少吨?
(2)若1辆A型货车需租金100元/次,1辆B型货车需租金120元/次,请问有几种租车方案?哪种最省钱?
25.(10分)综合与实践
【问题情境】数学活动课上,老师准备了若干张正方形纸片ABCD,组织同学们进行折纸探究活动.
【初步尝试】把正方形对折,折痕为EF,然后展开,点B落在点B'处,连接 B'C,请直接写出∠AEB'与∠ECB'的数量关系.
【能力提升】把正方形对折,折痕为EF,然后展开,使点B落在EF上的点P处,连接PD,猜想∠APD的度数,并说明理由.
【拓展延伸】在图2的条件下,作点A关于直线CP的对称点A',连接PA′,AC,如图3
26.(10分)综合与探究.
如图1,在平面直角坐标系中,已知二次函数,B两点(点A在点B的左侧),与y轴交于点C
(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式;
(2)点P是二次函数图象上的一个动点,请问是否存在点P使∠PCB=∠ABC?若存在,请求出点P的坐标,请说明理由;
(3)如图2,作出该二次函数图象的对称轴直线l,交x轴于点D.若点M是二次函数图象上一动点,作直线AM,BM,F,在点M的运动过程中,DE+DF的值是否为定值?若是;若不是,请说明理由.
参考答案与试题解析
一、选择题(共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)
1.2023的相反数是( )
A. B. C.2023 D.﹣2023
【分析】只有符号不同的两个数叫做互为相反数,由此即可得到答案.
【解答】解:2023的相反数是﹣2023.
故选:D.
【点评】本题考查相反数,关键是掌握相反数的定义.
2.随着我国航天领域的快速发展,从“天宫一号”发射升空,到天和核心舱归位,其图标既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形与轴对称图形的概念进行判断即可.
【解答】解:A、原图不是轴对称图形,故此选项不合题意;
B、原图既是中心对称图形,故此选项符合题意;
C、原图是轴对称图形,故此选项不合题意;
D、原图不是中心对称图形,故此选项不合题意;
故选:B.
【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
3.截至5月17日,南水北调东中线一期工程已累计向北方输水超6.2×1010立方米,直接受益人口超1.5亿人,其中6.2×1010立方米可表示为( )
A.6.2亿立方米 B.62亿立方米
C.620亿立方米 D.6200亿立方米
【分析】逆运用科学记数法的定义进行求解.
【解答】解:6.2×1010=620×107=620亿,
故选:C.
【点评】此题考查了科学记数法的逆运用能力,关键是能准确理解并运用科学记数法的定义.
4.下列运算正确的是( )
A.a3+a2=a5 B.(a4)2=a8
C.a6÷a2=a3 D.﹣3(a﹣b)=﹣3a﹣3b
【分析】根据同底数幂的除法,去括号与添括号,幂的乘方与积的乘方,合并同类项法则进行计算,逐一判断即可解答.
【解答】解:A、a3与a2不能合并,故A不符合题意;
B、(a5)2=a8,故B符合题意;
C、a7÷a2=a4,故C不符合题意;
D、﹣3(a﹣b)=﹣3a+3b;
故选:B.
【点评】本题考查了同底数幂的除法,去括号与添括号,幂的乘方与积的乘方,合并同类项,准确熟练地进行计算是解题的关键.
5.在直角坐标系中,点A的坐标为(2,﹣3),那么点A关于原点对称的点A1的坐标是( )
A.(﹣2,3) B.(﹣2,﹣3) C.(2,3) D.(﹣3,﹣2)
【分析】直接利用关于原点对称点的坐标特点即可得出答案.
【解答】解:∵点A的坐标为(2,﹣3),
∴点A关于原点对称的点A4的坐标是(﹣2,3).
故选:A.
【点评】此题主要考查了关于原点对称点的坐标特点,谁两个点关于原点对称时,它们的坐标符号相反是解题关键.
6.如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转( )
A.10° B.20° C.30° D.40°
【分析】由平行线的判定“同位角相等,两直线平行”可知,∠EGB=∠EHD时,AB∥CD,即∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°即可.
【解答】解:当∠EGB=∠EHD时,AB∥CD,
∵∠EGB=100°,∠EHD=80°,
∴∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°.
故选:B.
【点评】本题主要考查平行线的性质与判定,熟知平行线的性质与判定定理是解题的关键.
7.若关于x的方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A.k>﹣1 B.k<﹣1 C.k≥﹣1且k≠0 D.k>﹣1且k≠0
【分析】根据△的意义得到k≠0且Δ=4﹣4k×(﹣1)>0,然后求出两不等式的公共部分即可.
【解答】解:∵x的方程kx2+2x﹣4=0有两个不相等的实数根,
∴k≠0且Δ=5﹣4k×(﹣1)>6,解得k>﹣1,
∴k的取值范围为k>﹣1且k≠3.
故选:D.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2﹣4ac:当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.也考查了一元二次方程的定义.
8.下列事件中,是必然事件的是( )
A.疫情期间,对从疫情高风险区归来的人员进行核酸检测,检测结果为阳性
B.任意画一个三角形,其内角和为180°
C.某校开展“喜迎二十大,筑梦向未来”主题学习活动中,抽到A同学分享发言
D.打开电视机,正在播放“天宫课堂”
【分析】根据事件发生的可能性大小判断即可.
【解答】解:A、疫情期间,检测结果为阳性,不符合题意;
B、任意画一个三角形,是必然事件;
C、某校开展“喜迎二十大,抽到A同学分享发言,不符合题意;
D、打开电视机,是随机事件;
故选:B.
【点评】本题考查的是三角形内角和定理,必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
9.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,引绳度之,余绳四尺五寸,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余4.5尺;将绳子对折再量木头,问木头长多少尺?可设木头长为x尺,绳子长为y尺( )
A. B.
C. D.
【分析】根据题意可以列出相应的方程组,本题得以解决.
【解答】解:由题意可得,
,
故选:A.
【点评】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
10.如图,在5×4的网格图中,每个小正方形的边长均为1.设经过格点A,B,则弧AD的弧长为( )
A.π B.π C.π D.π
【分析】连接AC,AD,根据的勾股定理得到AC=AB==,BC==,根据勾股定理的逆定理得到∠ACB=90°,根据圆周角定理得到∠ADB=90°,根据弧长公式即可得到结论.
【解答】解:连接AC,AD,
∵AC=AB==,BC==,
∴AC7+AB2=BC2,
∴∠ACB=90°,
∴△ABC是等腰直角三角形,
∵∠AEB=90°,
∴AB是圆的直径,
∴∠ADB=90°,
∴AD⊥BD,
∴∠ABD=∠DAB=45°,
∴弧AD所对的圆心角为90°,
∴的长==π,
故选:C.
【点评】本题主要考查的是弧长的计算、等腰直角三角形的判定,锐角三角函数的性质,掌握本题的辅助线的作法是解题的关键.
11.某天早晨7:00,小龚从家骑自行车去上学,途中因自行车发生故障,修好车后继续骑行,7:20赶到了学校,结合图象,判断下列结论正确的是( )
A.小龚修好车后骑行到学校的平均速度是3m/s
B.小龚家距离学校750m
C.小龚修好车后花了20分钟到达学校
D.小龚修车花了10分钟
【分析】根据横坐标,可得时间;根据函数图象的纵坐标,可得路程.
【解答】解:A.由题意可知=2.5(m/s);
B.由纵坐标看出,故本选项不合题意;
C.由横坐标看出,故本选项不合题意;
D.小龚修车花了:15﹣4=10(分钟).
故选:D.
【点评】本题考查了函数图象,观察函数图象得出相应的时间,函数图象的纵坐标得出路程是解题关键.
12.如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,AE∥OB,反比例函数,若 OA=6,OC=4( )
A.6 B.11.25 C.12 D.18
【分析】连接DE,交AB于F,先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,证出四边形AEBD是菱形,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;把点E坐标代入求出k的值即可.
【解答】解:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,OA=6,
∴DA=ACOB,AB=OC=3,
∴DA=DB,
∴四边形AEBD是菱形;
连接DE,交AB于F
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=6,OC=4,
∴EF=DF=OA=3AB=2,
∴点E坐标为:(3,2).
∵反比例函数的图象经过点E,
∴k=5×2=18,
故选:D.
【点评】本题考查了平行四边形的判定、菱形的判定、矩形的性质、坐标与图形特征以及反比例函数解析式的求法;本题综合性强,有一定难度.
二、填空题(本大题共6小题,每小题2分,共12分.)
13.(2分)化简= 3 .
【分析】利用二次根式的运算法则进行化简即可.
【解答】解:=×=5,
故答案为:3.
【点评】本题考查利用二次根式的运算法则将其化为最简二次根式,其相关运算法则是基础且重要知识点,必须熟练掌握.
14.(2分)已知分式=0,则x= ﹣3 .
【分析】让分子为0,分母不为0列式求值即可.
【解答】解:由题意得:,
解①得:x=±6,
解②得x≠3,
∴x=﹣3,
故答案为﹣5.
【点评】考查分式值为0的条件;用到的知识点为:分式值为0,分子为0,分母不为0.
15.(2分)明珠塔楼是一栋古代工艺与现代精工艺完美融合的中式建筑.数学活动课上,老师带领兴趣小组去测量明珠塔的高度.如图,在C处用高0.5米的测倾器CE测得塔顶A的仰角为30°,在D处测得塔顶A的仰角为 60°,则明珠塔的高约为 (23+0.5) 米(结果保留根号).
【分析】设AG=x米,分别在Rt△AFG和Rt△AEG中,表示出FG和GE的长度,然后根据CD=40米,求出x的值,继而可求出明珠塔的高度AB.
【解答】解:如图,
设AG=x米,
在Rt△AFG中,∠AFG=60°=,
∴FG=x,
在Rt△AEG中,∠AEG=30°,
∴EG=x,
∴x﹣,
解得:x=23.
∴AG=23米,
则AB=(23+0.5)米.
答:明珠塔的高AB为(23+0.5)米.
故答案为:(23+0.5).
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.
16.(2分)有一组数据:3,a,4,6,7.它们的平均数是5,那么这组数据的方差是 2 .
【分析】先由平均数的公式计算出a的值,再根据方差的公式计算.一般地设n个数据,x1,x2,…,xn的平均数为,=(x1+x2+…+xn),则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
【解答】解:a=5×5﹣3﹣4﹣6﹣8=5,
s2=[(3﹣3)2+(5﹣5)2+(4﹣3)2+(6﹣5)2+(7﹣2)2]=2.
故答案为:5.
【点评】本题考查了方差的定义:一般地设n个数据,x1,x2,…,xn的平均数为,=(x1+x2+…+xn),则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
17.(2分)在平面直角坐标系中,一次函数y=2x+3的图象与x轴的交点坐标是 (﹣,0) .
【分析】令一次函数解析式中y=0,则可得出关于x的一元一次方程,解方程得出x值,从而得出一次函数图象与x轴的交点坐标.
【解答】解:令y=2x+3中y=6,则2x+3=8,
解得:x=﹣.
∴一次函数y=﹣4x+3的图象与x轴的交点坐标为(﹣,0).
故答案为:(﹣,0).
【点评】本题考查了一次函数图象上点的坐标特征.本题属于基础题,难度不大,解决该题型题目时,令一次函数解析式中y(或x)=0,求出x(或y)值是关键.
18.(2分)如图,将半径为4,圆心角为90°的扇形ABC绕弧AC的中点P逆时针旋转 45°,B,C的对应点分别为点D,E,F,点D落在AB上,则图中阴影部分的面积为 4π+8﹣16 .
【分析】设DE与BC的交点为Q,连接BP、DP、AP,过点P作PG⊥AB于点G,由S弓形AP=S弓形DP可得S阴影=S扇形ABC﹣S△ADP﹣S△DBQ,再证△BPG,△DBQ是等腰直角三角形,求出相关线段长度,进而求出S△ADP,S△DBQ,代入计算即可.
【解答】解:如图,设DE与BC的交点为Q、DP,过点P作PG⊥AB于点G,
∵扇形ABC绕点P逆时针旋转45°得到扇形DEF,
∴S弓形AP=S弓形DP,扇形ABC中空白部分的面积=S△ADP+S△DBQ,
∴S阴影=S扇形ABC﹣S△ADP﹣S△DBQ.
∵AP=DP,
∴△ADP是等腰三角形,
∴AG=GD,
∵∠ABC=90°,P为弧AC的中点,
∴∠ABP=45°,
∴△BPG是等腰直角三角形,
∵BP=4,
∴GB=GP=2,
∴AG=4﹣2,
∴AD=8﹣4,
∴S△ADP= AD PG=)×6﹣2,
∵∠PDQ=∠PAD,
∴∠QDB=45°,
∴△DBQ为等腰直角三角形,
∴S△DBQ=BD3=(3﹣AD)2=24﹣16,
∵S扇形ABC==4π,
∴S阴影=8﹣(4﹣16﹣16.
故答案为:4π+8﹣16.
【点评】本题考查旋转的性质,扇形的面积,等腰三角形的判定和性质等,解题的关键是通过推导得出S阴影=S扇形ABC﹣S△ADP﹣S△DBQ.
三、解答题(本大题共8小题,满分72分,解答应写出文字说明、证明过程或演算步骤)
19.(6分)计算:(﹣3)2×3﹣1+(﹣8+5)+tan60°
【分析】根据负整数指数幂,有理数的乘方,有理数的乘法,有理数的加法,特殊锐角三角函数值进行计算即可.
【解答】解:原式=9×+(﹣3)+
=5﹣3+
=.
【点评】本题考查实数的混合运算,其相关运算法则是基础且重要知识点,必须熟练掌握.
20.(6分)先化简,再求值:
,其中x=﹣1,y=2.
【分析】根据平方差公式、完全平方公式和多项式除以单项式将题目中的式子展开,然后合并同类项,最后将x、y的值代入化简后的式子计算即可.
【解答】解:
=x6﹣y2+x2﹣6xy+y2+xy﹣4
=8x2﹣xy﹣4,
当x=﹣3,y=2时2﹣(﹣5)×2﹣4=3.
【点评】本题考查分式的化简求值,熟练掌握运算法则是解答本题的关键,注意平方差公式和完全平方公式的应用.
21.(10分)如图,AB为⊙O的直径,点C在⊙O上.
(1)尺规作图(不写作法,保留作图痕迹):在⊙O上作点D,使得线段DB=DC,
且线段AD与BC相交;
(2)在(1)的条件下,AD与BC相交于点P,求∠ADC 的度数.
【分析】(1)根据垂径定理,作BC的垂直平分线即可;
(2)根据圆周角定理求解.
【解答】解:(1)如图:点D即为所求;
(2)∵∠ABP=∠BAP,
∴AC=BD,
∵DB=DC,
∴AC=BD=CD,
∴∠ADC=30°.
【点评】本题考查了复杂作图,掌握圆周角定理是解题的关键.
22.(10分)阅读理解学习
如图1,在△ABC中,AB=AC,P是BC边上一点,PM,AC垂直,垂足分别为M,N,有 S△ABC=S△ABP+S△ACP,即,由AB=AC 可得 BD=PM+PN.
请你模仿小刚的思路或者用你的新思路解决以下问题:
(1)如图2,当点P在CB的延长线上,且上面问题中其它条件不变时,PM,PN之间的数量关系 BD=PM﹣PN .
(2)如图3,当点P是△ABC 内一点,且 AB=AC=BC,PM,PN,AC,BC垂直,N,Q,猜想此时线段BD,PM,PQ之间的数量关系是 BD=PM+PN+PQ .并说明理由.
【分析】(1)连接PA,由△ABC的面积=△APC的面积﹣△APB的面积,得到AC BD=AC PN﹣AB PM,又AB=AC,即可推出BD=PM﹣PN;
(2)连接PA、PB、PC,由△ABC的面积=△PAB的面积+△PAC的面积+△PBC的面积,得到AC BD=AB PM+AC PN+BC PQ,又AB=AC=BC,即可证明BD=PM+PN+PQ.
【解答】解:(1)BD=PM﹣PN,理由如下:
连接PA,
∵PN⊥AC,BD⊥AC,
∴△APC的面积=AC PNAB PMAC BD,
∵△ABC的面积=△APC的面积﹣△APB的面积,
∴AC BD=AB PM,
∵AB=AC,
∴BD=PM﹣PN,
故答案为:BD=PM﹣PN.
(2)BD=PM+PN+PQ,理由如下:
连接PA、PB,
∵BD是△ABC 的高,PM,PQ分别与直线AB,BC垂直,
∴△ABC的面积=AC BDAB PMAC PNBC PQ,
∵△ABC的面积=△PAB的面积+△PAC的面积+△PBC的面积,
∴AC BD=AC PN+,
∵AB=AC=BC,
∴BD=PM+PN+PQ,
故答案为:BD=PM+PN+PQ.
【点评】本题考查三角形的面积,等腰三角形、等边三角形的性质,关键是由三角形面积公式来解决问题.
23.(10分)2022年是我国航天事业辉煌的一年,神舟十四号和神舟十五号两个飞行乘组6位航天员在太空会师,在神州大地上掀起了航天热潮,在全校范围内开展了航天知识竞赛,学校随机抽取了50名学生的成绩
组号 成绩 频数 频率
1 140≤x<50 2 0.04
2 50≤x<60 a 0.1
3 60≤x<70 18 0.36
4 70≤x<80 9 0.18
5 80≤x<90 b m
6 90≤x≤100 2 0.05
合计 50 1.000
其中60≤x<70这一组的数据如下:
61,62,62,64,64,64,64,64,64,64,66,67,69
根据以上提供的信息,解答下列问题:
(1)表格中a= 5 ,b= 14 ,m= 0.28 ;
(2)60≤x<70这一组数据的众数是 64 ,中位数是 64 ;
(3)若以组中值(每组正中间数值)为本组数据的平均数,全校共有1500名学生参与竞赛
【分析】(1)根据频数=频率×总数及各组频数之和等于总数求解即可;
(2)根据众数和中位数的定义求解即可;
(3)利用加权平均数的定义及样本估计总体求解即可.
【解答】解:(1)a=50×0.1=4,b=50﹣(2+5+18+2+2)=14,
∴m=14÷50=0.28,
故答案为:2,14;
(2)根据60≤x<70这一组的数据:61,62,64,64,64,64,64,64,64,69;
中位数是:=64,
故答案为:64,64;
(3)×(45×5+55×5+65×18+75×9+85×14+95×7)=71.8(分),
答:估计所有学生成绩的平均分约为71.8分.
【点评】本题考查频数分布直方图、用样本估计总体、中位数,解答本题的关键是明确题意,利用数形结合的思想解答.
24.(10分)为实现“乡村振兴”战略目标,某乡镇制定了“以产业带动发展”的策略,开发出了某新型农产品,B两种型号的货车将该农产品运往外地销售,已知用1辆A型车和2辆B型车载满该农产品一次可运11吨,计划一次运完,且每辆车都满载.
(1)1辆A型货车和1辆B型货车满载时一次分别运该农产品多少吨?
(2)若1辆A型货车需租金100元/次,1辆B型货车需租金120元/次,请问有几种租车方案?哪种最省钱?
【分析】(1)设1辆A型货车载满该农产品一次可运送x吨,1辆B型货车载满该农产品一次可运送y吨,根据“用2辆A型车和1辆B型车载满洋葱一次可运走10吨;用1辆A型车和2辆B型车载满洋葱一次可运走11吨”,列出二元一次方程组,解之即可;
(2)设租用A型货车α辆,B型货车b辆,根据一次运送31吨该农产品,即可得出关于a,b的二元一次方程,解之a,b均为非负整数,即可得出各租车方案;
【解答】解:(1)设1辆A型货车载满该农产品一次可运送x吨,1辆B型货车载满该农产品一次可运送y吨,
由题意可得:,
解得:,
答:1辆A型货车载满该农产品一次可运送3吨,6辆B型货车载满该农产品一次可运送4吨;
(2)设租用A型货车α辆,B型货车b辆,
由题意可得:3a+3b=31,
∴a=,
又∵a,b均为非负整数,
∴或或,
∴该物流公司共有5种租车方案,
方案1:租用9辆A型车,4辆B型车;
方案2:租用5辆A型车,3辆B型车;
方案3:租用1辆A型车,7辆B型车,
∴方案1的费用:9×100+4×120=1020元,
方案2的费用:5×100+8×120=980元,
方案1的费用:1×100+2×120=940元,
∵1020>980>940,
∴方案3最省钱.
【点评】本题考查了二元一次方程组的应用,二次一次方程的应用,找到正确的数量关系是解题的关键.
25.(10分)综合与实践
【问题情境】数学活动课上,老师准备了若干张正方形纸片ABCD,组织同学们进行折纸探究活动.
【初步尝试】把正方形对折,折痕为EF,然后展开,点B落在点B'处,连接 B'C,请直接写出∠AEB'与∠ECB'的数量关系.
【能力提升】把正方形对折,折痕为EF,然后展开,使点B落在EF上的点P处,连接PD,猜想∠APD的度数,并说明理由.
【拓展延伸】在图2的条件下,作点A关于直线CP的对称点A',连接PA′,AC,如图3
【分析】(1)连接BB',由折叠的性质证出BE=BE',∠AEB=∠AEB',BB'⊥AE,得出AE∥CB',由平行线的性质得出∠AEB=∠ECB',则可得出结论;
(2)证明△APD是等边三角形,由等边三角形的性质得出∠APD=60°;
(3)连接A'C、AA',证明△AA'B≌△CA'B(SSS),得出∠AA'B=∠CA'B=∠AA'C=30°,则可得出答案.
【解答】解:(1)∠AEB'=∠ECB'.
连接BB',
∵把正方形对折,
∴E为BC的中点,
∴BE=CE,
∵沿过点A与点E所在的直线折叠,点B落在点B'处,
∴BE=BE',∠AEB=∠AEB',
∴BE=CE=BE'
∴∠BB'C=90°,
∴AE∥CB',
∴∠AEB=∠ECB',
∴∠AEB'=∠ECB';
(2)猜想:∠APD=60°.
理由:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ADC=90°,
由折叠性质可得:,EF⊥AD.
∴PA=PD=AD,
∴△APD是等边三角形,
∴∠APD=60°;
(3)解:连接A'C、AA',
由(2)得△APD是等边三角形,
∴∠PAD=∠PDA=∠APD=60°,AP=DP=AD,
∵∠ADC=90°,
∴∠PDC=30°,
又∵PD=AD=DC,
∴∠DPC=∠DCP=,∠DAC=∠DCA=45°,
∴∠PAC=∠PAD﹣∠DAC=60°﹣45°=15°,∠ACP=∠DCP﹣∠DCA=75°﹣45°=30°.
由对称性质得:AC=A'C,∠ACP=∠A'CP=30°,
∴∠ACA'=60°,
∴△ACA'是等边三角形,
在△AA'B 与△CA'B中,
,
∴△AA'B≌△CA'B(SSS),
∴∠AA'B=∠CA'B=∠AA'C=30°,
又∵∠CA'P=∠CAP=15°,
∴∠PA'B=∠CA'B﹣∠CA'P=15°.
【点评】本题是几何变换综合题,考查了折叠的性质,正方形的性质,全等三角形的判定与性质,等边三角形的判定与性质,熟练掌握正方形的性质和翻折变换的性质是解题的关键.
26.(10分)综合与探究.
如图1,在平面直角坐标系中,已知二次函数,B两点(点A在点B的左侧),与y轴交于点C
(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式;
(2)点P是二次函数图象上的一个动点,请问是否存在点P使∠PCB=∠ABC?若存在,请求出点P的坐标,请说明理由;
(3)如图2,作出该二次函数图象的对称轴直线l,交x轴于点D.若点M是二次函数图象上一动点,作直线AM,BM,F,在点M的运动过程中,DE+DF的值是否为定值?若是;若不是,请说明理由.
【分析】(1)先根据二次函数的性质求出A,B,C的坐标,再利用待定系数法求一次函数解析式;
(2)分两种情况讨论,当点P在BC上方时,当点P在BC下方时,再利用勾股定理和待定系数法进行求解即可;
(3)由(2)得抛物线的对称轴为直线x=1,求出点D的坐标,设且﹣1<t<3,分别求出直线AM的解析式和直线BM的解析式,进而表示出,即可求解.
【解答】解:(1)当y=0时,即,
解得:x8=﹣1,x2=4.
∴图象与x轴交于点A(﹣1,0),6),
当x=0时,y=2,4),
∴直线BC的函数表达式为;
(2)存在,理由如下:
当点P在BC上方时,
∵∠PCB=∠ABC,
∴CP∥AB,即CP∥x轴,
∴点P与点C关于抛物线的对称轴对称,
∵,
∴抛物线的对称轴为直线;
∵C(0,2),
∴P(8,2);
当点P在BC下方时,设CP交x轴于点K(m,
则OK=m,KB=3﹣m.
∵∠PCB=∠ABC,
∴CK=BK=5﹣m.
在Rt△COK中,OC2+OK2=CK4,
∴22+m3=(3﹣m)2,
解得:,
∴,
设直线CK的解析式为y=kx+d,
,
解得:,
∴直线CK的解析式为,
联立,得,
解得:(舍去),,
∴.
综上所述,点P的坐标为(2;
(3)存在,DE+DF的值为定值
由(2)得抛物线的对称轴为直线x=1,
∴D(4,0),
设且﹣1<t<4,
设直线AM的解析式为y=k1x+b1,
将A(﹣6,0)和点M的坐标代入得:
,
解得:,
∴直线AM的解析式为,
当x=7时,,
∴,
同理,直线BM的解析式为:,
当x=1时,,
∴,
∴,
∴,
∴DE+DF的值是定值,.
【点评】本题考查了二次函数的综合题目,涉及待定系数法求一次函数解析式,二次函数解析式,二次函数的图象和性质,熟练掌握知识点是解题的关键.
一、选择题(共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)
1.2023的相反数是( )
A. B. C.2023 D.﹣2023
2.随着我国航天领域的快速发展,从“天宫一号”发射升空,到天和核心舱归位,其图标既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.截至5月17日,南水北调东中线一期工程已累计向北方输水超6.2×1010立方米,直接受益人口超1.5亿人,其中6.2×1010立方米可表示为( )
A.6.2亿立方米 B.62亿立方米
C.620亿立方米 D.6200亿立方米
4.下列运算正确的是( )
A.a3+a2=a5 B.(a4)2=a8
C.a6÷a2=a3 D.﹣3(a﹣b)=﹣3a﹣3b
5.在直角坐标系中,点A的坐标为(2,﹣3),那么点A关于原点对称的点A1的坐标是( )
A.(﹣2,3) B.(﹣2,﹣3) C.(2,3) D.(﹣3,﹣2)
6.如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转( )
A.10° B.20° C.30° D.40°
7.若关于x的方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A.k>﹣1 B.k<﹣1 C.k≥﹣1且k≠0 D.k>﹣1且k≠0
8.下列事件中,是必然事件的是( )
A.疫情期间,对从疫情高风险区归来的人员进行核酸检测,检测结果为阳性
B.任意画一个三角形,其内角和为180°
C.某校开展“喜迎二十大,筑梦向未来”主题学习活动中,抽到A同学分享发言
D.打开电视机,正在播放“天宫课堂”
9.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,引绳度之,余绳四尺五寸,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余4.5尺;将绳子对折再量木头,问木头长多少尺?可设木头长为x尺,绳子长为y尺( )
A. B.
C. D.
10.如图,在5×4的网格图中,每个小正方形的边长均为1.设经过格点A,B,则弧AD的弧长为( )
A.π B.π C.π D.π
11.某天早晨7:00,小龚从家骑自行车去上学,途中因自行车发生故障,修好车后继续骑行,7:20赶到了学校,结合图象,判断下列结论正确的是( )
A.小龚修好车后骑行到学校的平均速度是3m/s
B.小龚家距离学校750m
C.小龚修好车后花了20分钟到达学校
D.小龚修车花了10分钟
12.如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,AE∥OB,反比例函数,若 OA=6,OC=4( )
A.6 B.11.25 C.12 D.18
二、填空题(本大题共6小题,每小题2分,共12分.)
13.(2分)化简= .
14.(2分)已知分式=0,则x= .
15.(2分)明珠塔楼是一栋古代工艺与现代精工艺完美融合的中式建筑.数学活动课上,老师带领兴趣小组去测量明珠塔的高度.如图,在C处用高0.5米的测倾器CE测得塔顶A的仰角为30°,在D处测得塔顶A的仰角为 60°,则明珠塔的高约为 米(结果保留根号).
16.(2分)有一组数据:3,a,4,6,7.它们的平均数是5,那么这组数据的方差是 .
17.(2分)在平面直角坐标系中,一次函数y=2x+3的图象与x轴的交点坐标是 .
18.(2分)如图,将半径为4,圆心角为90°的扇形ABC绕弧AC的中点P逆时针旋转 45°,B,C的对应点分别为点D,E,F,点D落在AB上,则图中阴影部分的面积为 .
三、解答题(本大题共8小题,满分72分,解答应写出文字说明、证明过程或演算步骤)
19.(6分)计算:(﹣3)2×3﹣1+(﹣8+5)+tan60°
20.(6分)先化简,再求值:
,其中x=﹣1,y=2.
21.(10分)如图,AB为⊙O的直径,点C在⊙O上.
(1)尺规作图(不写作法,保留作图痕迹):在⊙O上作点D,使得线段DB=DC,
且线段AD与BC相交;
(2)在(1)的条件下,AD与BC相交于点P,求∠ADC 的度数.
22.(10分)阅读理解学习
如图1,在△ABC中,AB=AC,P是BC边上一点,PM,AC垂直,垂足分别为M,N,有 S△ABC=S△ABP+S△ACP,即,由AB=AC 可得 BD=PM+PN.
请你模仿小刚的思路或者用你的新思路解决以下问题:
(1)如图2,当点P在CB的延长线上,且上面问题中其它条件不变时,PM,PN之间的数量关系 .
(2)如图3,当点P是△ABC 内一点,且 AB=AC=BC,PM,PN,AC,BC垂直,N,Q,猜想此时线段BD,PM,PQ之间的数量关系是 .并说明理由.
23.(10分)2022年是我国航天事业辉煌的一年,神舟十四号和神舟十五号两个飞行乘组6位航天员在太空会师,在神州大地上掀起了航天热潮,在全校范围内开展了航天知识竞赛,学校随机抽取了50名学生的成绩
组号 成绩 频数 频率
1 140≤x<50 2 0.04
2 50≤x<60 a 0.1
3 60≤x<70 18 0.36
4 70≤x<80 9 0.18
5 80≤x<90 b m
6 90≤x≤100 2 0.05
合计 50 1.000
其中60≤x<70这一组的数据如下:
61,62,62,64,64,64,64,64,64,64,66,67,69
根据以上提供的信息,解答下列问题:
(1)表格中a= ,b= ,m= ;
(2)60≤x<70这一组数据的众数是 ,中位数是 ;
(3)若以组中值(每组正中间数值)为本组数据的平均数,全校共有1500名学生参与竞赛
24.(10分)为实现“乡村振兴”战略目标,某乡镇制定了“以产业带动发展”的策略,开发出了某新型农产品,B两种型号的货车将该农产品运往外地销售,已知用1辆A型车和2辆B型车载满该农产品一次可运11吨,计划一次运完,且每辆车都满载.
(1)1辆A型货车和1辆B型货车满载时一次分别运该农产品多少吨?
(2)若1辆A型货车需租金100元/次,1辆B型货车需租金120元/次,请问有几种租车方案?哪种最省钱?
25.(10分)综合与实践
【问题情境】数学活动课上,老师准备了若干张正方形纸片ABCD,组织同学们进行折纸探究活动.
【初步尝试】把正方形对折,折痕为EF,然后展开,点B落在点B'处,连接 B'C,请直接写出∠AEB'与∠ECB'的数量关系.
【能力提升】把正方形对折,折痕为EF,然后展开,使点B落在EF上的点P处,连接PD,猜想∠APD的度数,并说明理由.
【拓展延伸】在图2的条件下,作点A关于直线CP的对称点A',连接PA′,AC,如图3
26.(10分)综合与探究.
如图1,在平面直角坐标系中,已知二次函数,B两点(点A在点B的左侧),与y轴交于点C
(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式;
(2)点P是二次函数图象上的一个动点,请问是否存在点P使∠PCB=∠ABC?若存在,请求出点P的坐标,请说明理由;
(3)如图2,作出该二次函数图象的对称轴直线l,交x轴于点D.若点M是二次函数图象上一动点,作直线AM,BM,F,在点M的运动过程中,DE+DF的值是否为定值?若是;若不是,请说明理由.
参考答案与试题解析
一、选择题(共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)
1.2023的相反数是( )
A. B. C.2023 D.﹣2023
【分析】只有符号不同的两个数叫做互为相反数,由此即可得到答案.
【解答】解:2023的相反数是﹣2023.
故选:D.
【点评】本题考查相反数,关键是掌握相反数的定义.
2.随着我国航天领域的快速发展,从“天宫一号”发射升空,到天和核心舱归位,其图标既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形与轴对称图形的概念进行判断即可.
【解答】解:A、原图不是轴对称图形,故此选项不合题意;
B、原图既是中心对称图形,故此选项符合题意;
C、原图是轴对称图形,故此选项不合题意;
D、原图不是中心对称图形,故此选项不合题意;
故选:B.
【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
3.截至5月17日,南水北调东中线一期工程已累计向北方输水超6.2×1010立方米,直接受益人口超1.5亿人,其中6.2×1010立方米可表示为( )
A.6.2亿立方米 B.62亿立方米
C.620亿立方米 D.6200亿立方米
【分析】逆运用科学记数法的定义进行求解.
【解答】解:6.2×1010=620×107=620亿,
故选:C.
【点评】此题考查了科学记数法的逆运用能力,关键是能准确理解并运用科学记数法的定义.
4.下列运算正确的是( )
A.a3+a2=a5 B.(a4)2=a8
C.a6÷a2=a3 D.﹣3(a﹣b)=﹣3a﹣3b
【分析】根据同底数幂的除法,去括号与添括号,幂的乘方与积的乘方,合并同类项法则进行计算,逐一判断即可解答.
【解答】解:A、a3与a2不能合并,故A不符合题意;
B、(a5)2=a8,故B符合题意;
C、a7÷a2=a4,故C不符合题意;
D、﹣3(a﹣b)=﹣3a+3b;
故选:B.
【点评】本题考查了同底数幂的除法,去括号与添括号,幂的乘方与积的乘方,合并同类项,准确熟练地进行计算是解题的关键.
5.在直角坐标系中,点A的坐标为(2,﹣3),那么点A关于原点对称的点A1的坐标是( )
A.(﹣2,3) B.(﹣2,﹣3) C.(2,3) D.(﹣3,﹣2)
【分析】直接利用关于原点对称点的坐标特点即可得出答案.
【解答】解:∵点A的坐标为(2,﹣3),
∴点A关于原点对称的点A4的坐标是(﹣2,3).
故选:A.
【点评】此题主要考查了关于原点对称点的坐标特点,谁两个点关于原点对称时,它们的坐标符号相反是解题关键.
6.如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转( )
A.10° B.20° C.30° D.40°
【分析】由平行线的判定“同位角相等,两直线平行”可知,∠EGB=∠EHD时,AB∥CD,即∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°即可.
【解答】解:当∠EGB=∠EHD时,AB∥CD,
∵∠EGB=100°,∠EHD=80°,
∴∠EGB需要变小20°,即将木棒AB绕点G逆时针旋转20°.
故选:B.
【点评】本题主要考查平行线的性质与判定,熟知平行线的性质与判定定理是解题的关键.
7.若关于x的方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A.k>﹣1 B.k<﹣1 C.k≥﹣1且k≠0 D.k>﹣1且k≠0
【分析】根据△的意义得到k≠0且Δ=4﹣4k×(﹣1)>0,然后求出两不等式的公共部分即可.
【解答】解:∵x的方程kx2+2x﹣4=0有两个不相等的实数根,
∴k≠0且Δ=5﹣4k×(﹣1)>6,解得k>﹣1,
∴k的取值范围为k>﹣1且k≠3.
故选:D.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2﹣4ac:当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.也考查了一元二次方程的定义.
8.下列事件中,是必然事件的是( )
A.疫情期间,对从疫情高风险区归来的人员进行核酸检测,检测结果为阳性
B.任意画一个三角形,其内角和为180°
C.某校开展“喜迎二十大,筑梦向未来”主题学习活动中,抽到A同学分享发言
D.打开电视机,正在播放“天宫课堂”
【分析】根据事件发生的可能性大小判断即可.
【解答】解:A、疫情期间,检测结果为阳性,不符合题意;
B、任意画一个三角形,是必然事件;
C、某校开展“喜迎二十大,抽到A同学分享发言,不符合题意;
D、打开电视机,是随机事件;
故选:B.
【点评】本题考查的是三角形内角和定理,必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
9.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,引绳度之,余绳四尺五寸,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长、绳子还剩余4.5尺;将绳子对折再量木头,问木头长多少尺?可设木头长为x尺,绳子长为y尺( )
A. B.
C. D.
【分析】根据题意可以列出相应的方程组,本题得以解决.
【解答】解:由题意可得,
,
故选:A.
【点评】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
10.如图,在5×4的网格图中,每个小正方形的边长均为1.设经过格点A,B,则弧AD的弧长为( )
A.π B.π C.π D.π
【分析】连接AC,AD,根据的勾股定理得到AC=AB==,BC==,根据勾股定理的逆定理得到∠ACB=90°,根据圆周角定理得到∠ADB=90°,根据弧长公式即可得到结论.
【解答】解:连接AC,AD,
∵AC=AB==,BC==,
∴AC7+AB2=BC2,
∴∠ACB=90°,
∴△ABC是等腰直角三角形,
∵∠AEB=90°,
∴AB是圆的直径,
∴∠ADB=90°,
∴AD⊥BD,
∴∠ABD=∠DAB=45°,
∴弧AD所对的圆心角为90°,
∴的长==π,
故选:C.
【点评】本题主要考查的是弧长的计算、等腰直角三角形的判定,锐角三角函数的性质,掌握本题的辅助线的作法是解题的关键.
11.某天早晨7:00,小龚从家骑自行车去上学,途中因自行车发生故障,修好车后继续骑行,7:20赶到了学校,结合图象,判断下列结论正确的是( )
A.小龚修好车后骑行到学校的平均速度是3m/s
B.小龚家距离学校750m
C.小龚修好车后花了20分钟到达学校
D.小龚修车花了10分钟
【分析】根据横坐标,可得时间;根据函数图象的纵坐标,可得路程.
【解答】解:A.由题意可知=2.5(m/s);
B.由纵坐标看出,故本选项不合题意;
C.由横坐标看出,故本选项不合题意;
D.小龚修车花了:15﹣4=10(分钟).
故选:D.
【点评】本题考查了函数图象,观察函数图象得出相应的时间,函数图象的纵坐标得出路程是解题关键.
12.如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,AE∥OB,反比例函数,若 OA=6,OC=4( )
A.6 B.11.25 C.12 D.18
【分析】连接DE,交AB于F,先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,证出四边形AEBD是菱形,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;把点E坐标代入求出k的值即可.
【解答】解:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,OA=6,
∴DA=ACOB,AB=OC=3,
∴DA=DB,
∴四边形AEBD是菱形;
连接DE,交AB于F
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=6,OC=4,
∴EF=DF=OA=3AB=2,
∴点E坐标为:(3,2).
∵反比例函数的图象经过点E,
∴k=5×2=18,
故选:D.
【点评】本题考查了平行四边形的判定、菱形的判定、矩形的性质、坐标与图形特征以及反比例函数解析式的求法;本题综合性强,有一定难度.
二、填空题(本大题共6小题,每小题2分,共12分.)
13.(2分)化简= 3 .
【分析】利用二次根式的运算法则进行化简即可.
【解答】解:=×=5,
故答案为:3.
【点评】本题考查利用二次根式的运算法则将其化为最简二次根式,其相关运算法则是基础且重要知识点,必须熟练掌握.
14.(2分)已知分式=0,则x= ﹣3 .
【分析】让分子为0,分母不为0列式求值即可.
【解答】解:由题意得:,
解①得:x=±6,
解②得x≠3,
∴x=﹣3,
故答案为﹣5.
【点评】考查分式值为0的条件;用到的知识点为:分式值为0,分子为0,分母不为0.
15.(2分)明珠塔楼是一栋古代工艺与现代精工艺完美融合的中式建筑.数学活动课上,老师带领兴趣小组去测量明珠塔的高度.如图,在C处用高0.5米的测倾器CE测得塔顶A的仰角为30°,在D处测得塔顶A的仰角为 60°,则明珠塔的高约为 (23+0.5) 米(结果保留根号).
【分析】设AG=x米,分别在Rt△AFG和Rt△AEG中,表示出FG和GE的长度,然后根据CD=40米,求出x的值,继而可求出明珠塔的高度AB.
【解答】解:如图,
设AG=x米,
在Rt△AFG中,∠AFG=60°=,
∴FG=x,
在Rt△AEG中,∠AEG=30°,
∴EG=x,
∴x﹣,
解得:x=23.
∴AG=23米,
则AB=(23+0.5)米.
答:明珠塔的高AB为(23+0.5)米.
故答案为:(23+0.5).
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.
16.(2分)有一组数据:3,a,4,6,7.它们的平均数是5,那么这组数据的方差是 2 .
【分析】先由平均数的公式计算出a的值,再根据方差的公式计算.一般地设n个数据,x1,x2,…,xn的平均数为,=(x1+x2+…+xn),则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
【解答】解:a=5×5﹣3﹣4﹣6﹣8=5,
s2=[(3﹣3)2+(5﹣5)2+(4﹣3)2+(6﹣5)2+(7﹣2)2]=2.
故答案为:5.
【点评】本题考查了方差的定义:一般地设n个数据,x1,x2,…,xn的平均数为,=(x1+x2+…+xn),则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
17.(2分)在平面直角坐标系中,一次函数y=2x+3的图象与x轴的交点坐标是 (﹣,0) .
【分析】令一次函数解析式中y=0,则可得出关于x的一元一次方程,解方程得出x值,从而得出一次函数图象与x轴的交点坐标.
【解答】解:令y=2x+3中y=6,则2x+3=8,
解得:x=﹣.
∴一次函数y=﹣4x+3的图象与x轴的交点坐标为(﹣,0).
故答案为:(﹣,0).
【点评】本题考查了一次函数图象上点的坐标特征.本题属于基础题,难度不大,解决该题型题目时,令一次函数解析式中y(或x)=0,求出x(或y)值是关键.
18.(2分)如图,将半径为4,圆心角为90°的扇形ABC绕弧AC的中点P逆时针旋转 45°,B,C的对应点分别为点D,E,F,点D落在AB上,则图中阴影部分的面积为 4π+8﹣16 .
【分析】设DE与BC的交点为Q,连接BP、DP、AP,过点P作PG⊥AB于点G,由S弓形AP=S弓形DP可得S阴影=S扇形ABC﹣S△ADP﹣S△DBQ,再证△BPG,△DBQ是等腰直角三角形,求出相关线段长度,进而求出S△ADP,S△DBQ,代入计算即可.
【解答】解:如图,设DE与BC的交点为Q、DP,过点P作PG⊥AB于点G,
∵扇形ABC绕点P逆时针旋转45°得到扇形DEF,
∴S弓形AP=S弓形DP,扇形ABC中空白部分的面积=S△ADP+S△DBQ,
∴S阴影=S扇形ABC﹣S△ADP﹣S△DBQ.
∵AP=DP,
∴△ADP是等腰三角形,
∴AG=GD,
∵∠ABC=90°,P为弧AC的中点,
∴∠ABP=45°,
∴△BPG是等腰直角三角形,
∵BP=4,
∴GB=GP=2,
∴AG=4﹣2,
∴AD=8﹣4,
∴S△ADP= AD PG=)×6﹣2,
∵∠PDQ=∠PAD,
∴∠QDB=45°,
∴△DBQ为等腰直角三角形,
∴S△DBQ=BD3=(3﹣AD)2=24﹣16,
∵S扇形ABC==4π,
∴S阴影=8﹣(4﹣16﹣16.
故答案为:4π+8﹣16.
【点评】本题考查旋转的性质,扇形的面积,等腰三角形的判定和性质等,解题的关键是通过推导得出S阴影=S扇形ABC﹣S△ADP﹣S△DBQ.
三、解答题(本大题共8小题,满分72分,解答应写出文字说明、证明过程或演算步骤)
19.(6分)计算:(﹣3)2×3﹣1+(﹣8+5)+tan60°
【分析】根据负整数指数幂,有理数的乘方,有理数的乘法,有理数的加法,特殊锐角三角函数值进行计算即可.
【解答】解:原式=9×+(﹣3)+
=5﹣3+
=.
【点评】本题考查实数的混合运算,其相关运算法则是基础且重要知识点,必须熟练掌握.
20.(6分)先化简,再求值:
,其中x=﹣1,y=2.
【分析】根据平方差公式、完全平方公式和多项式除以单项式将题目中的式子展开,然后合并同类项,最后将x、y的值代入化简后的式子计算即可.
【解答】解:
=x6﹣y2+x2﹣6xy+y2+xy﹣4
=8x2﹣xy﹣4,
当x=﹣3,y=2时2﹣(﹣5)×2﹣4=3.
【点评】本题考查分式的化简求值,熟练掌握运算法则是解答本题的关键,注意平方差公式和完全平方公式的应用.
21.(10分)如图,AB为⊙O的直径,点C在⊙O上.
(1)尺规作图(不写作法,保留作图痕迹):在⊙O上作点D,使得线段DB=DC,
且线段AD与BC相交;
(2)在(1)的条件下,AD与BC相交于点P,求∠ADC 的度数.
【分析】(1)根据垂径定理,作BC的垂直平分线即可;
(2)根据圆周角定理求解.
【解答】解:(1)如图:点D即为所求;
(2)∵∠ABP=∠BAP,
∴AC=BD,
∵DB=DC,
∴AC=BD=CD,
∴∠ADC=30°.
【点评】本题考查了复杂作图,掌握圆周角定理是解题的关键.
22.(10分)阅读理解学习
如图1,在△ABC中,AB=AC,P是BC边上一点,PM,AC垂直,垂足分别为M,N,有 S△ABC=S△ABP+S△ACP,即,由AB=AC 可得 BD=PM+PN.
请你模仿小刚的思路或者用你的新思路解决以下问题:
(1)如图2,当点P在CB的延长线上,且上面问题中其它条件不变时,PM,PN之间的数量关系 BD=PM﹣PN .
(2)如图3,当点P是△ABC 内一点,且 AB=AC=BC,PM,PN,AC,BC垂直,N,Q,猜想此时线段BD,PM,PQ之间的数量关系是 BD=PM+PN+PQ .并说明理由.
【分析】(1)连接PA,由△ABC的面积=△APC的面积﹣△APB的面积,得到AC BD=AC PN﹣AB PM,又AB=AC,即可推出BD=PM﹣PN;
(2)连接PA、PB、PC,由△ABC的面积=△PAB的面积+△PAC的面积+△PBC的面积,得到AC BD=AB PM+AC PN+BC PQ,又AB=AC=BC,即可证明BD=PM+PN+PQ.
【解答】解:(1)BD=PM﹣PN,理由如下:
连接PA,
∵PN⊥AC,BD⊥AC,
∴△APC的面积=AC PNAB PMAC BD,
∵△ABC的面积=△APC的面积﹣△APB的面积,
∴AC BD=AB PM,
∵AB=AC,
∴BD=PM﹣PN,
故答案为:BD=PM﹣PN.
(2)BD=PM+PN+PQ,理由如下:
连接PA、PB,
∵BD是△ABC 的高,PM,PQ分别与直线AB,BC垂直,
∴△ABC的面积=AC BDAB PMAC PNBC PQ,
∵△ABC的面积=△PAB的面积+△PAC的面积+△PBC的面积,
∴AC BD=AC PN+,
∵AB=AC=BC,
∴BD=PM+PN+PQ,
故答案为:BD=PM+PN+PQ.
【点评】本题考查三角形的面积,等腰三角形、等边三角形的性质,关键是由三角形面积公式来解决问题.
23.(10分)2022年是我国航天事业辉煌的一年,神舟十四号和神舟十五号两个飞行乘组6位航天员在太空会师,在神州大地上掀起了航天热潮,在全校范围内开展了航天知识竞赛,学校随机抽取了50名学生的成绩
组号 成绩 频数 频率
1 140≤x<50 2 0.04
2 50≤x<60 a 0.1
3 60≤x<70 18 0.36
4 70≤x<80 9 0.18
5 80≤x<90 b m
6 90≤x≤100 2 0.05
合计 50 1.000
其中60≤x<70这一组的数据如下:
61,62,62,64,64,64,64,64,64,64,66,67,69
根据以上提供的信息,解答下列问题:
(1)表格中a= 5 ,b= 14 ,m= 0.28 ;
(2)60≤x<70这一组数据的众数是 64 ,中位数是 64 ;
(3)若以组中值(每组正中间数值)为本组数据的平均数,全校共有1500名学生参与竞赛
【分析】(1)根据频数=频率×总数及各组频数之和等于总数求解即可;
(2)根据众数和中位数的定义求解即可;
(3)利用加权平均数的定义及样本估计总体求解即可.
【解答】解:(1)a=50×0.1=4,b=50﹣(2+5+18+2+2)=14,
∴m=14÷50=0.28,
故答案为:2,14;
(2)根据60≤x<70这一组的数据:61,62,64,64,64,64,64,64,64,69;
中位数是:=64,
故答案为:64,64;
(3)×(45×5+55×5+65×18+75×9+85×14+95×7)=71.8(分),
答:估计所有学生成绩的平均分约为71.8分.
【点评】本题考查频数分布直方图、用样本估计总体、中位数,解答本题的关键是明确题意,利用数形结合的思想解答.
24.(10分)为实现“乡村振兴”战略目标,某乡镇制定了“以产业带动发展”的策略,开发出了某新型农产品,B两种型号的货车将该农产品运往外地销售,已知用1辆A型车和2辆B型车载满该农产品一次可运11吨,计划一次运完,且每辆车都满载.
(1)1辆A型货车和1辆B型货车满载时一次分别运该农产品多少吨?
(2)若1辆A型货车需租金100元/次,1辆B型货车需租金120元/次,请问有几种租车方案?哪种最省钱?
【分析】(1)设1辆A型货车载满该农产品一次可运送x吨,1辆B型货车载满该农产品一次可运送y吨,根据“用2辆A型车和1辆B型车载满洋葱一次可运走10吨;用1辆A型车和2辆B型车载满洋葱一次可运走11吨”,列出二元一次方程组,解之即可;
(2)设租用A型货车α辆,B型货车b辆,根据一次运送31吨该农产品,即可得出关于a,b的二元一次方程,解之a,b均为非负整数,即可得出各租车方案;
【解答】解:(1)设1辆A型货车载满该农产品一次可运送x吨,1辆B型货车载满该农产品一次可运送y吨,
由题意可得:,
解得:,
答:1辆A型货车载满该农产品一次可运送3吨,6辆B型货车载满该农产品一次可运送4吨;
(2)设租用A型货车α辆,B型货车b辆,
由题意可得:3a+3b=31,
∴a=,
又∵a,b均为非负整数,
∴或或,
∴该物流公司共有5种租车方案,
方案1:租用9辆A型车,4辆B型车;
方案2:租用5辆A型车,3辆B型车;
方案3:租用1辆A型车,7辆B型车,
∴方案1的费用:9×100+4×120=1020元,
方案2的费用:5×100+8×120=980元,
方案1的费用:1×100+2×120=940元,
∵1020>980>940,
∴方案3最省钱.
【点评】本题考查了二元一次方程组的应用,二次一次方程的应用,找到正确的数量关系是解题的关键.
25.(10分)综合与实践
【问题情境】数学活动课上,老师准备了若干张正方形纸片ABCD,组织同学们进行折纸探究活动.
【初步尝试】把正方形对折,折痕为EF,然后展开,点B落在点B'处,连接 B'C,请直接写出∠AEB'与∠ECB'的数量关系.
【能力提升】把正方形对折,折痕为EF,然后展开,使点B落在EF上的点P处,连接PD,猜想∠APD的度数,并说明理由.
【拓展延伸】在图2的条件下,作点A关于直线CP的对称点A',连接PA′,AC,如图3
【分析】(1)连接BB',由折叠的性质证出BE=BE',∠AEB=∠AEB',BB'⊥AE,得出AE∥CB',由平行线的性质得出∠AEB=∠ECB',则可得出结论;
(2)证明△APD是等边三角形,由等边三角形的性质得出∠APD=60°;
(3)连接A'C、AA',证明△AA'B≌△CA'B(SSS),得出∠AA'B=∠CA'B=∠AA'C=30°,则可得出答案.
【解答】解:(1)∠AEB'=∠ECB'.
连接BB',
∵把正方形对折,
∴E为BC的中点,
∴BE=CE,
∵沿过点A与点E所在的直线折叠,点B落在点B'处,
∴BE=BE',∠AEB=∠AEB',
∴BE=CE=BE'
∴∠BB'C=90°,
∴AE∥CB',
∴∠AEB=∠ECB',
∴∠AEB'=∠ECB';
(2)猜想:∠APD=60°.
理由:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ADC=90°,
由折叠性质可得:,EF⊥AD.
∴PA=PD=AD,
∴△APD是等边三角形,
∴∠APD=60°;
(3)解:连接A'C、AA',
由(2)得△APD是等边三角形,
∴∠PAD=∠PDA=∠APD=60°,AP=DP=AD,
∵∠ADC=90°,
∴∠PDC=30°,
又∵PD=AD=DC,
∴∠DPC=∠DCP=,∠DAC=∠DCA=45°,
∴∠PAC=∠PAD﹣∠DAC=60°﹣45°=15°,∠ACP=∠DCP﹣∠DCA=75°﹣45°=30°.
由对称性质得:AC=A'C,∠ACP=∠A'CP=30°,
∴∠ACA'=60°,
∴△ACA'是等边三角形,
在△AA'B 与△CA'B中,
,
∴△AA'B≌△CA'B(SSS),
∴∠AA'B=∠CA'B=∠AA'C=30°,
又∵∠CA'P=∠CAP=15°,
∴∠PA'B=∠CA'B﹣∠CA'P=15°.
【点评】本题是几何变换综合题,考查了折叠的性质,正方形的性质,全等三角形的判定与性质,等边三角形的判定与性质,熟练掌握正方形的性质和翻折变换的性质是解题的关键.
26.(10分)综合与探究.
如图1,在平面直角坐标系中,已知二次函数,B两点(点A在点B的左侧),与y轴交于点C
(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式;
(2)点P是二次函数图象上的一个动点,请问是否存在点P使∠PCB=∠ABC?若存在,请求出点P的坐标,请说明理由;
(3)如图2,作出该二次函数图象的对称轴直线l,交x轴于点D.若点M是二次函数图象上一动点,作直线AM,BM,F,在点M的运动过程中,DE+DF的值是否为定值?若是;若不是,请说明理由.
【分析】(1)先根据二次函数的性质求出A,B,C的坐标,再利用待定系数法求一次函数解析式;
(2)分两种情况讨论,当点P在BC上方时,当点P在BC下方时,再利用勾股定理和待定系数法进行求解即可;
(3)由(2)得抛物线的对称轴为直线x=1,求出点D的坐标,设且﹣1<t<3,分别求出直线AM的解析式和直线BM的解析式,进而表示出,即可求解.
【解答】解:(1)当y=0时,即,
解得:x8=﹣1,x2=4.
∴图象与x轴交于点A(﹣1,0),6),
当x=0时,y=2,4),
∴直线BC的函数表达式为;
(2)存在,理由如下:
当点P在BC上方时,
∵∠PCB=∠ABC,
∴CP∥AB,即CP∥x轴,
∴点P与点C关于抛物线的对称轴对称,
∵,
∴抛物线的对称轴为直线;
∵C(0,2),
∴P(8,2);
当点P在BC下方时,设CP交x轴于点K(m,
则OK=m,KB=3﹣m.
∵∠PCB=∠ABC,
∴CK=BK=5﹣m.
在Rt△COK中,OC2+OK2=CK4,
∴22+m3=(3﹣m)2,
解得:,
∴,
设直线CK的解析式为y=kx+d,
,
解得:,
∴直线CK的解析式为,
联立,得,
解得:(舍去),,
∴.
综上所述,点P的坐标为(2;
(3)存在,DE+DF的值为定值
由(2)得抛物线的对称轴为直线x=1,
∴D(4,0),
设且﹣1<t<4,
设直线AM的解析式为y=k1x+b1,
将A(﹣6,0)和点M的坐标代入得:
,
解得:,
∴直线AM的解析式为,
当x=7时,,
∴,
同理,直线BM的解析式为:,
当x=1时,,
∴,
∴,
∴,
∴DE+DF的值是定值,.
【点评】本题考查了二次函数的综合题目,涉及待定系数法求一次函数解析式,二次函数解析式,二次函数的图象和性质,熟练掌握知识点是解题的关键.
同课章节目录
