15.3.2完全平方公式
图片预览






文档简介
课件14张PPT。15.3.2 完全平方公式15.3.2 完全平方公式探究
计算下列各式,你能发现什么规律?
(p+1)2 = (p+1) (p+1) = ______
(m+2)2= _________;
(p-1)2 = (p-1 ) (p-1) = ________;
(m-2)2 = __________.P2+2p+1m2+4m+4P2-2p+1m2-4m+4我们来计算(a+b)2, (a-b)2.(a+b)2=(a+b) (a+b) = a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2
=a2-2ab+b2一般地,我们有
即两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.
这两个公式叫做(乘法的)完全平方公式. (a+b)2=a2+2ab+b2,
(a-b) 2 = a2-2ab +b2.
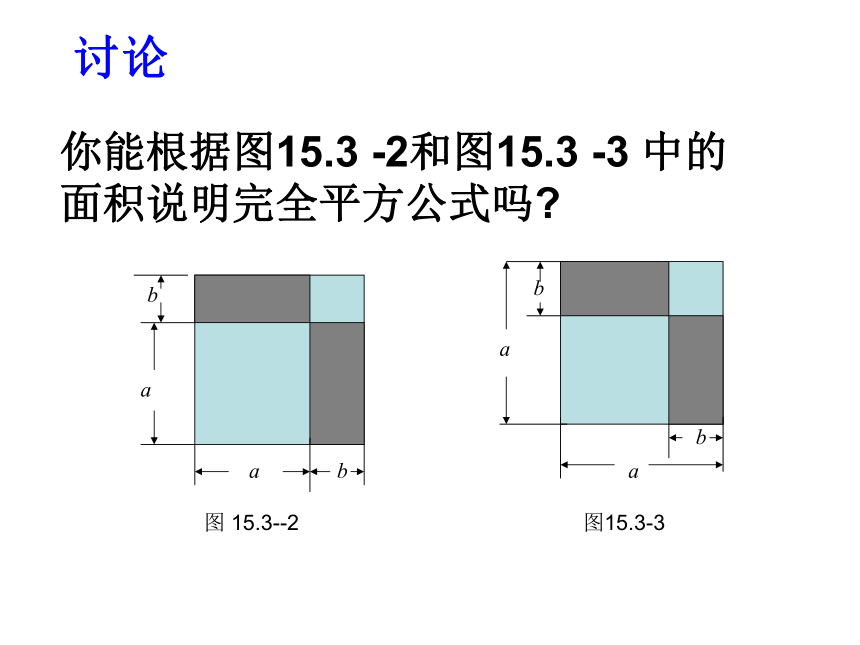
你能根据图15.3 -2和图15.3 -3 中的面积说明完全平方公式吗?讨论例3 运用完全平方公式计算:
(1) (4m+n)2; (2) (y- )2.解: (1) (4m+n) 2= (4m)2 + 2?(4m)?n+n2
= 16m2+8mn +n2;
(2) (y - )2 = y2 - 2?y? + ( )2
= y2-y + 例4 运用完全平方公式计算:
(1) 1022 ; (2) 992 .解: (1) 1022 = (100 +2) 2
= 1002 +2Χ100Χ2 + 22
= 10 000 +400 +4
= 10 404 .(2) 992 = (100 -1)2
= 1002 -2Χ100Χ1+12
= 10 000 - 200 + 1
= 9 801.思考
(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2与a2-b2相等吗?
为什么?练习
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
2.下面各式的计算错在哪里?应当怎样改正?
(1) (a+ b)2 = a2 +b2;
(2) (a – b) 2 =a2 – b2.添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号.a+(b+c) = a+b+c; a- (b+c) = a - b – c.a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .例5 运用乘法公式计算:
(1) ( x +2y-3) (x- 2y +3) ; (2) (a + b +c ) 2.解: (1) ( x +2y-3) (x- 2y +3)
= [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9.(a + b +c ) 2
= [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac.练习
1.在等号右边的括号内填上适当的项:
(1) a + b + c = a + ( );
a – b – c = a – ( ) ;
a - b + c = a – ( );
a + b + c = a - ( ).能否用去括号法则检查添括号是否正确?2.运用乘法公式计算:
(a + 2b – 1 ) 2 ;
(2x +y +z ) (2x – y – z )3.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.再见
计算下列各式,你能发现什么规律?
(p+1)2 = (p+1) (p+1) = ______
(m+2)2= _________;
(p-1)2 = (p-1 ) (p-1) = ________;
(m-2)2 = __________.P2+2p+1m2+4m+4P2-2p+1m2-4m+4我们来计算(a+b)2, (a-b)2.(a+b)2=(a+b) (a+b) = a2+ab+ab+b2
=a2+2ab+b2.
(a-b)2 = (a-b) (a-b) = a2-ab-ab+b2
=a2-2ab+b2一般地,我们有
即两数和(或差)的平方,等于它们的平方和,加(或减)它们的积的2倍.
这两个公式叫做(乘法的)完全平方公式. (a+b)2=a2+2ab+b2,
(a-b) 2 = a2-2ab +b2.
你能根据图15.3 -2和图15.3 -3 中的面积说明完全平方公式吗?讨论例3 运用完全平方公式计算:
(1) (4m+n)2; (2) (y- )2.解: (1) (4m+n) 2= (4m)2 + 2?(4m)?n+n2
= 16m2+8mn +n2;
(2) (y - )2 = y2 - 2?y? + ( )2
= y2-y + 例4 运用完全平方公式计算:
(1) 1022 ; (2) 992 .解: (1) 1022 = (100 +2) 2
= 1002 +2Χ100Χ2 + 22
= 10 000 +400 +4
= 10 404 .(2) 992 = (100 -1)2
= 1002 -2Χ100Χ1+12
= 10 000 - 200 + 1
= 9 801.思考
(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2与a2-b2相等吗?
为什么?练习
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
2.下面各式的计算错在哪里?应当怎样改正?
(1) (a+ b)2 = a2 +b2;
(2) (a – b) 2 =a2 – b2.添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号.a+(b+c) = a+b+c; a- (b+c) = a - b – c.a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .例5 运用乘法公式计算:
(1) ( x +2y-3) (x- 2y +3) ; (2) (a + b +c ) 2.解: (1) ( x +2y-3) (x- 2y +3)
= [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9.(a + b +c ) 2
= [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac.练习
1.在等号右边的括号内填上适当的项:
(1) a + b + c = a + ( );
a – b – c = a – ( ) ;
a - b + c = a – ( );
a + b + c = a - ( ).能否用去括号法则检查添括号是否正确?2.运用乘法公式计算:
(a + 2b – 1 ) 2 ;
(2x +y +z ) (2x – y – z )3.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.再见
