【名师解析】湖南省长郡中学2015届高三月考试卷(三)数学(文)试题
文档属性
| 名称 | 【名师解析】湖南省长郡中学2015届高三月考试卷(三)数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 386.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-28 08:22:43 | ||
图片预览




文档简介
【名师解析】湖南省长郡中学2015届高三月考试卷(三)数学(文)试题
【试卷综述】本试卷注重对数学基础知识、基本技能、基本思想和方法的考查,突出了对数学的计算能力、逻辑思维能力等方面的考察。突出考查数学主干知识 ,侧重于中学数学学科的基础知识和基本技能的考查;侧重于知识交汇点的考查。注重双基和数学思想数学方法的复习,注重运算能力思维能力的培养。较多试题是以综合题的形式出现,在考查学生基础知识的同时,能考查学生的能力。
【题文】一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
【题文】1.设集合,则
A. B. C. D.
【知识点】 指数、对数不等式的解法;集合运算. E1 A1
【答案】【解析】B解析:,所以,
故选B.
【思路点拨】先化简集合A、B,再利用补集、交集的意义求结论.
【题文】2.复数(i是虚数单位)的虚部是
A. B. C. D.
【知识点】复数运算. L4
【答案】【解析】D解析:因为=,所以其虚部是,
故选D.
【思路点拨】利用复数运算,把已知复数化为a+bi,形式即可.
【题文】3.下列命题错误的是
A.命题“若则”的逆否命题为“若则”
B.若为假命题,则均为假命题
C.命题存在使得,则任意都有
D.“x>2”是“”的充分不必要条件
【知识点】 命题及其关系;基本逻辑联结词及量词. A2 A3
【答案】【解析】B解析:显然命题A正确;对于命题B:若为假命题,则中至少有一个为假命题 .所以命题B是错误的,故选B.
【思路点拨】逐个分析每个命题的正误即得结论.
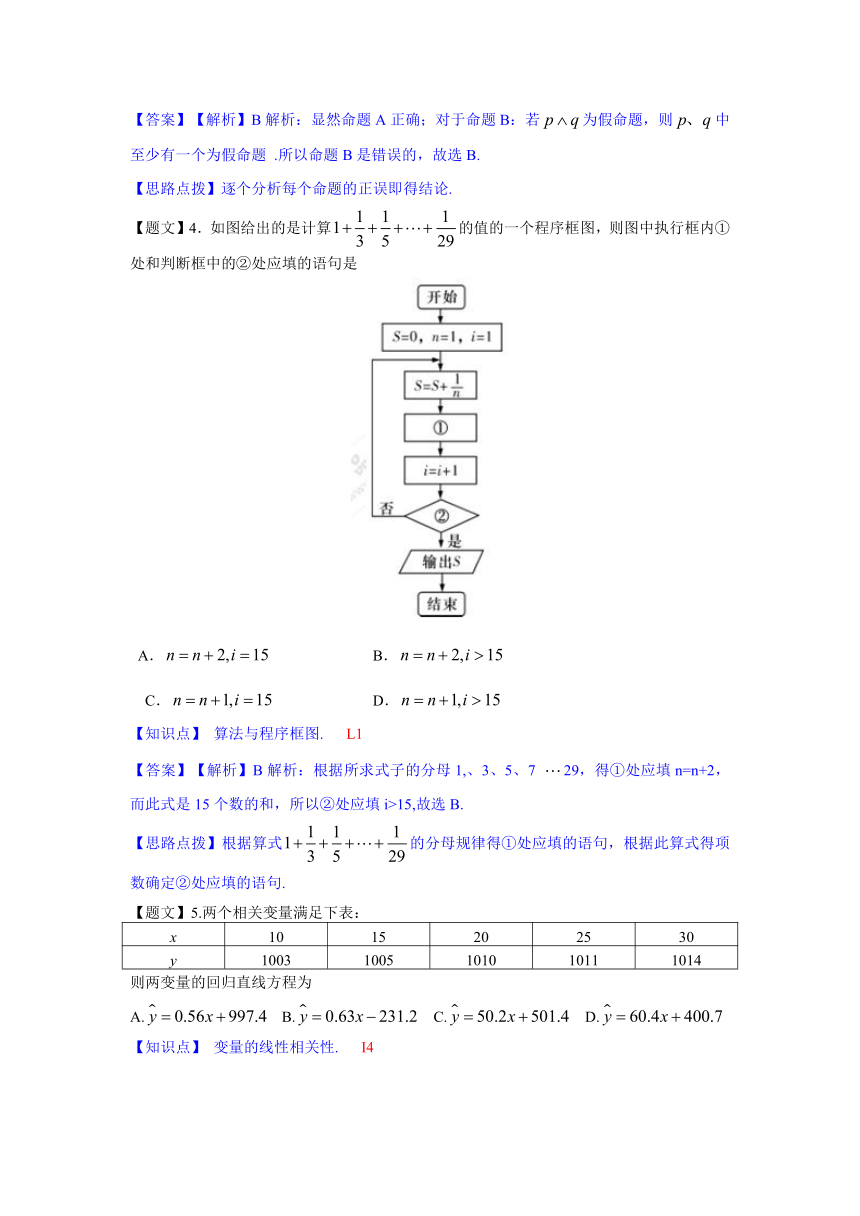
【题文】4.如图给出的是计算的值的一个程序框图,则图中执行框内①处和判断框中的②处应填的语句是
A. B.
C. D.
【知识点】 算法与程序框图. L1
【答案】【解析】B解析:根据所求式子的分母1,、3、5、7 29,得①处应填n=n+2,而此式是15个数的和,所以②处应填i>15,故选B.
【思路点拨】根据算式的分母规律得①处应填的语句,根据此算式得项数确定②处应填的语句.
【题文】5.两个相关变量满足下表:
x
10
15
20
25
30
y
1003
1005
1010
1011
1014
则两变量的回归直线方程为
A. B. C. D.
【知识点】 变量的线性相关性. I4
【答案】【解析】A解析:,,
,故选A.
【思路点拨】先求出样本中心点,再用最小二乘法求得即可.
【题文】6.已知函数把方程的根按从小到大的顺序排成一个数列,则该数列的前n项和为
A. B.
C. D.
【知识点】 函数与方程. B9
【答案】【解析】B解析:,所以 方程的根按从小到大的顺序排成一个数列为:0、1、2、3、4、,所以该数列的前n项和为
,故选B.
【思路点拨】根据已知条件写出函数f(x)表达式的规律,其与y=x交点横坐标依次为0、1、2、3、4,所以所求为.
【题文】7.一个几何体的三视图如图所示,则这个几何体的体积等于
A.12 B.4 C. D.
【知识点】几何体的三视图. G2
【答案】【解析】B解析:由三视图可知此几何体是底面为直角梯形(其上底长2,下底长4,高2),高为2的四棱锥,所以其体积为,故选B.
【思路点拨】由几何体的三视图得此几何体的结构,从而求得该几何体的体积.
【题文】8.已知点F1、F2分别是椭圆的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率e是
A. B. C. D.
【知识点】 椭圆的几何性质. H5
【答案】【解析】D解析:设A在第二象限,则A的纵坐标是,因为中,
,,所以,与
联立得离心率.故选D.
【思路点拨】由已知得是,的
直角三角形,由此得关于a,b,c的等量关系,再与联立得离心率.
【题文】9.已知函数,若恒成立,则ab的最大值为
A. B. C. D.
【知识点】 导数法确定不等式恒成立的条件;B12 E8
【答案】【解析】D解析:因为,所以时 f(x)是增函数,不恒成立,当a>0时,=0得x=lna,易得f(x)在x=lna处有最小值,要使恒成立,需使,即,
所以,
设,易得函数在
处有最大值,所以ab的最大值为,故选D.
【思路点拨】利用导数确定函数恒成立的条件为(a>0),从而得:
,然后再用导数求的最大值即可.
【题文】10.A,B,C是平面内不共线的三点,点P在该平面内且有,现将一粒芝麻随机撒在△ABC内,则这粒芝麻落在△PBC内的概率为
A. B. C. D.
【知识点】几何概型. K3
【答案】【解析】D解析:由
,
得,设C到AB距离d,如图,则:,
,所以
,所以所求概率为 .故选D.
【思路点拨】根据已知确定点P位置,结合图形求与面积等量关系.
【题文】二、填空题:本大题共5小题,每小题5分,共25分。把答案填在答题卡中对应题号后的横线上.
【题文】11.已知x,y满足约束条件,且的最小值为-6,则常数k=______.
【知识点】 简单的线性规划问题. E5
【答案】【解析】0解析:画出可行域如图,平移目标函数得点B(3,-3-k)为最优解,所以.
【思路点拨】画出可行域,平移目标函数,确定最优解,代入目标函数求得k值.
【题文】12.在极坐标系中,直线被圆截得的弦长为______.
【知识点】 极坐标的意义. N3
【答案】【解析】解析:直线的直角坐标方程为,
圆的 直角坐标方程为,因为圆心(0,0)到直线的距离d=2,半径r=4,
所以截得的弦长为.
【思路点拨】先把直线和圆的极坐标方程化为直角坐标方程,再利用直角坐标方程求弦长.
【题文】13.过原点作曲线的切线,则切线方程为________________.
【知识点】导数的几何意义. B11
【答案】【解析】解析:设的、切点(a,lna),由,所以切线方程为,此直线过原点,得a=e,所以所求切线方程为.
【思路点拨】设出切点坐标,由导数求得斜率关于切点横坐标的表达式,从而得切线方程,再由切线过原点得,切点横坐标,进一步得结论.
【题文】14.已知不等式对任意恒成立,则实数m的取值范围是______.
【知识点】指数不等式解法;不等式恒成立的条件. E1 E8
【答案】【解析】-3【思路点拨】利用指数函数单调性,将已知转化为一元二次不等式恒成立问题即可.
【题文】15. 设△AnBnCn的三边长分别为an,bn,cn,n=1,2,3…,若
,则的最大值是________________.
【知识点】 数列;函数最值. D1 B3
【答案】【解析】解析:由得
,又,所以
,而,所以,所以
,所以的最大值是
【思路点拨】由已知得数列{}是常数列,代入余弦定理,再由基本不等式求得的最小值,从而得的最大值.
【题文】三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
【题文】16.(本小题满分12分)
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定综合得分85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
【知识点】用样本估计总体;茎叶图;古典概型. I2 K2
【答案】【解析】(1) 东城区的平均分较高;(2).解析:(1) 根据茎叶图知,东城区的平均分为
西城区的平均分为,
∴东城区的平均分较高.………………………………………………………(5分)
(2)从两个区域各选一个优秀厂家,所有的基本事件数为种,
满足得分差距不超过5分的事件:
9种,
∴满足条件的概率为…………………………………………………………(12分)
【思路点拨】(1)根据平均数得定义求得东、西两个城区厂家的平均分;(2)用列举法写出
从两个区域各选一个优秀厂家的所有情况共15种,其中满足得分差距不超过5分的情况有9种,所以满足条件的概率为.
【题文】17.(本小题满分12分)
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE=,平面ABCD⊥平面ABE.
(1)求证:平面ADE⊥平面BCE;
(2)求三棱锥D—ACE的体积.
【知识点】线面垂直的判定;锥体的体积公式. G5 G1
【答案】【解析】(1)证明:见解析;(2)解析:(1)∵四边形ABCD是正方形,
∴AD⊥AB.又∵平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,AD平面ABCD,
∴AD⊥平面ABE,而BE平面ABE,∴AD⊥BE.
又∵AE=BE=,AB=2,∴,∴AE⊥BE.
而AD∩AE=A,AD、AE平面ADE,∴BE⊥平面ADE,而BE平面BCE,
∴平面ADE⊥平面BCE.……………………………………………(6分)
(2)取AB的中点O,连接OE,∵△ABE是等腰三角形,∴OE⊥AB.
又∵AD⊥平面ABE,OE平面ABE,∴AD⊥OE,∴OE⊥平面ABCD,
即OE是三棱锥D—ACE的高.又∵AB=AE=BE=2,∴OE=1,
∴.--------(12分)
【思路点拨】(1)根据线面垂直的判定定理,只需在平面BCE内找到直线与平面ADE垂直即可,易知此直线是BE;(2)利用等体积转化法,转化为求三棱锥E-ACD的体积即可.
【题文】18.(本小题满分12分)
设记
(1)求函数的最小正周期;
(2)试用“五点法”画出函数在区间的简图,并指出该函数的图象可由的图象经过怎样的平移和伸缩变换得到;
(3)若时,函数的最小值为2,试求出函数的最大值并指出x取何值时,函数取得最大值.
【知识点】 向量的数量积;二倍角公式;两角和与差的三角函数;函数的图像与性质;F3 C6 C5 C4
【答案】【解析】(1);(2)见解析;(2)时取得最大,最大值为
解析:(1)
, ∴………………………………(3分)
(2)
x
0
0
1
0
-1
0
y
向左平移得到,再保持纵坐标不变,横坐标缩短为原的变为,最后再向上平移个单位得到.……………(8分)
(3)
当即时取得最大,最大值为………………………………(12分)
【思路点拨】(1)利用向量数量积得坐标公式,二倍角公式,两角和与差的三角函数公式,求得,从而得函数的最小正周期;(2)计算时的范围,从而确定“五点法”中的关键点,然后列表、描点、画出图像;可以将
的图像先平移再横伸缩变换得y图像.也可以先进行横伸缩变换再 进行平移变换得y图像;(3)先计算时的范围,
从而得最值关于m的表达式,进而求得结论.
【题文】19.(本小题满分13分)
已知等差数列满足.
(1)求的通项公式; (2)若,数列满足关系式
求证:数列的通项公式为
(3)设(2)中的数列的前项和Sn,对任意的正整数n,
恒成立,求实数p的取值范围.
【知识点】等差数列;已知递推公式求通项;不等式恒成立问题. D2 D1 E8
【答案】【解析】(1)(2)证明:见解析;(3).
解析:(1)设等差数列的公差为d,由已知,有解得
所以即等差数列的通项公式为(3分)
(2)因为所以当时,.
证:当时,,所以
将这n-1个式子相加,得即.
当n=1时,也满足上式.
所以数列的通项公式为.……………………………………(7分)
(3)由(2),所以
所以原不等式变为即
所以对任意恒成立,所以
所以p的取值范围是.……………………………………………………(13分)
【思路点拨】(1)利用已知求得首项和公差即可;(2)累加法证明结论;(3)由(2)中结论化简恒成立的不等式,即对任意恒成立,而,所以
【题文】20.(本小题满分13分)
已知椭圆以坐标原点为中心,坐标轴为对称轴,且椭圆以抛物线y2 =16x的焦点为其一个焦点,以双曲线的焦点为顶点.
(1)求椭圆的标准方程;
(2)已知点A(-1,0),B(1,0),且C,D分别为椭圆的上顶点和右顶点,点P是线段CD上的动点,求的取值范围;
(3)试问在圆上是否存在一点M,使△F1MF2的面积(其中a为椭圆的半长轴长,b为椭圆的半短轴长,F1,F2为椭圆的两个焦点),若存在,求的值;若不存在,请说明理由.
【知识点】 椭圆的方程;向量数量积坐标运算;三角形的面积公式. H5 F3
【答案】【解析】(1);(2);(3)存在点M且=2.
解析:(1)因为抛物线y2=16x的焦点坐标和双曲线的焦点分别为(4,0)和(5,0).
所以所以椭圆的标准方程:.…………………………(3分)
(2)设,则
则当OP⊥CD时,取到最小值,即:
当点P在D点时,取到最大值:OD=5.所以:.……………(7分)
(3)如图所示:
由第一问可知,圆的方程为.△F1MF2的面积
设M(x,y),又△F1MF2的面积
又F1(-4,0),F2(4,0),设直线MF2的倾斜角为,直线MF1的倾斜角为,则
即的值为2.………………………………………………………………(13分)
【思路点拨】(1)由已知得椭圆中的参数a,b,c的值即可;(2)求得线段CD方程
,设出点得向量坐标,从而得
,再化为关于的函数,由得的取值范围;
(3)由(1)得出圆的方程为.△F1MF2的面积不妨设M在x轴上方,结合图形可得点M的纵坐标,进一步求得的三角函数值.
【题文】21.(本小题满分13分)
已知函数
(1)当a=0时,求的极值;
(2)当a<0时,求的单调区间;
(3)若对任意当及,恒有成立,求实数m的取值范围.
【知识点】 导数的应用;不等式恒成立问题. B12 E8
【答案】【解析】(1)的极小值为无极大值;(2)当时,的递减区间为和,递增区间为;当时,在上单调递减;当时,的递减区间为和,递增区间为;
(3)
解析:(1)依题意知的定义域为,
当时,
令,解得当时,;当时,.
又∵∴的极小值为无极大值.………………(3分)
(2)
当时,令得或,
令得当时,得
令得,令得
当时,
综上所述,当时,的递减区间为和,递增区间为;
当时,在上单调递减;
当时,的递减区间为和,递增区间为.…(8分)
(3)由(2)可知,当时,在区间上单调递减;
当x=1时,取得最大值;当x=3时,取得最小值;
恒成立,
,整理得,
恒成立,
………………………………………………………………(13分)
【思路点拨】(1)通过判断导函数为零的点两侧,导函数值的符号,确定极值情况;
(2)通过对a取值的讨论,确定:导函数大于零的x范围是增区间,导函数小于零的范围是减区间;(3)由(2)的结论,化简恒成立的不等式为:,
恒成立,由此求得实数m的取值范围.
【典例剖析】本题第(3)小问是不等式恒成立问题,虽然是常见题型,但本题有一定难度.
需要利用第(2)小问的结论求在上的最大值,从而转化为常规的恒成立问题求解.
【试卷综述】本试卷注重对数学基础知识、基本技能、基本思想和方法的考查,突出了对数学的计算能力、逻辑思维能力等方面的考察。突出考查数学主干知识 ,侧重于中学数学学科的基础知识和基本技能的考查;侧重于知识交汇点的考查。注重双基和数学思想数学方法的复习,注重运算能力思维能力的培养。较多试题是以综合题的形式出现,在考查学生基础知识的同时,能考查学生的能力。
【题文】一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
【题文】1.设集合,则
A. B. C. D.
【知识点】 指数、对数不等式的解法;集合运算. E1 A1
【答案】【解析】B解析:,所以,
故选B.
【思路点拨】先化简集合A、B,再利用补集、交集的意义求结论.
【题文】2.复数(i是虚数单位)的虚部是
A. B. C. D.
【知识点】复数运算. L4
【答案】【解析】D解析:因为=,所以其虚部是,
故选D.
【思路点拨】利用复数运算,把已知复数化为a+bi,形式即可.
【题文】3.下列命题错误的是
A.命题“若则”的逆否命题为“若则”
B.若为假命题,则均为假命题
C.命题存在使得,则任意都有
D.“x>2”是“”的充分不必要条件
【知识点】 命题及其关系;基本逻辑联结词及量词. A2 A3
【答案】【解析】B解析:显然命题A正确;对于命题B:若为假命题,则中至少有一个为假命题 .所以命题B是错误的,故选B.
【思路点拨】逐个分析每个命题的正误即得结论.
【题文】4.如图给出的是计算的值的一个程序框图,则图中执行框内①处和判断框中的②处应填的语句是
A. B.
C. D.
【知识点】 算法与程序框图. L1
【答案】【解析】B解析:根据所求式子的分母1,、3、5、7 29,得①处应填n=n+2,而此式是15个数的和,所以②处应填i>15,故选B.
【思路点拨】根据算式的分母规律得①处应填的语句,根据此算式得项数确定②处应填的语句.
【题文】5.两个相关变量满足下表:
x
10
15
20
25
30
y
1003
1005
1010
1011
1014
则两变量的回归直线方程为
A. B. C. D.
【知识点】 变量的线性相关性. I4
【答案】【解析】A解析:,,
,故选A.
【思路点拨】先求出样本中心点,再用最小二乘法求得即可.
【题文】6.已知函数把方程的根按从小到大的顺序排成一个数列,则该数列的前n项和为
A. B.
C. D.
【知识点】 函数与方程. B9
【答案】【解析】B解析:,所以 方程的根按从小到大的顺序排成一个数列为:0、1、2、3、4、,所以该数列的前n项和为
,故选B.
【思路点拨】根据已知条件写出函数f(x)表达式的规律,其与y=x交点横坐标依次为0、1、2、3、4,所以所求为.
【题文】7.一个几何体的三视图如图所示,则这个几何体的体积等于
A.12 B.4 C. D.
【知识点】几何体的三视图. G2
【答案】【解析】B解析:由三视图可知此几何体是底面为直角梯形(其上底长2,下底长4,高2),高为2的四棱锥,所以其体积为,故选B.
【思路点拨】由几何体的三视图得此几何体的结构,从而求得该几何体的体积.
【题文】8.已知点F1、F2分别是椭圆的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率e是
A. B. C. D.
【知识点】 椭圆的几何性质. H5
【答案】【解析】D解析:设A在第二象限,则A的纵坐标是,因为中,
,,所以,与
联立得离心率.故选D.
【思路点拨】由已知得是,的
直角三角形,由此得关于a,b,c的等量关系,再与联立得离心率.
【题文】9.已知函数,若恒成立,则ab的最大值为
A. B. C. D.
【知识点】 导数法确定不等式恒成立的条件;B12 E8
【答案】【解析】D解析:因为,所以时 f(x)是增函数,不恒成立,当a>0时,=0得x=lna,易得f(x)在x=lna处有最小值,要使恒成立,需使,即,
所以,
设,易得函数在
处有最大值,所以ab的最大值为,故选D.
【思路点拨】利用导数确定函数恒成立的条件为(a>0),从而得:
,然后再用导数求的最大值即可.
【题文】10.A,B,C是平面内不共线的三点,点P在该平面内且有,现将一粒芝麻随机撒在△ABC内,则这粒芝麻落在△PBC内的概率为
A. B. C. D.
【知识点】几何概型. K3
【答案】【解析】D解析:由
,
得,设C到AB距离d,如图,则:,
,所以
,所以所求概率为 .故选D.
【思路点拨】根据已知确定点P位置,结合图形求与面积等量关系.
【题文】二、填空题:本大题共5小题,每小题5分,共25分。把答案填在答题卡中对应题号后的横线上.
【题文】11.已知x,y满足约束条件,且的最小值为-6,则常数k=______.
【知识点】 简单的线性规划问题. E5
【答案】【解析】0解析:画出可行域如图,平移目标函数得点B(3,-3-k)为最优解,所以.
【思路点拨】画出可行域,平移目标函数,确定最优解,代入目标函数求得k值.
【题文】12.在极坐标系中,直线被圆截得的弦长为______.
【知识点】 极坐标的意义. N3
【答案】【解析】解析:直线的直角坐标方程为,
圆的 直角坐标方程为,因为圆心(0,0)到直线的距离d=2,半径r=4,
所以截得的弦长为.
【思路点拨】先把直线和圆的极坐标方程化为直角坐标方程,再利用直角坐标方程求弦长.
【题文】13.过原点作曲线的切线,则切线方程为________________.
【知识点】导数的几何意义. B11
【答案】【解析】解析:设的、切点(a,lna),由,所以切线方程为,此直线过原点,得a=e,所以所求切线方程为.
【思路点拨】设出切点坐标,由导数求得斜率关于切点横坐标的表达式,从而得切线方程,再由切线过原点得,切点横坐标,进一步得结论.
【题文】14.已知不等式对任意恒成立,则实数m的取值范围是______.
【知识点】指数不等式解法;不等式恒成立的条件. E1 E8
【答案】【解析】-3
【题文】15. 设△AnBnCn的三边长分别为an,bn,cn,n=1,2,3…,若
,则的最大值是________________.
【知识点】 数列;函数最值. D1 B3
【答案】【解析】解析:由得
,又,所以
,而,所以,所以
,所以的最大值是
【思路点拨】由已知得数列{}是常数列,代入余弦定理,再由基本不等式求得的最小值,从而得的最大值.
【题文】三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
【题文】16.(本小题满分12分)
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定综合得分85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
【知识点】用样本估计总体;茎叶图;古典概型. I2 K2
【答案】【解析】(1) 东城区的平均分较高;(2).解析:(1) 根据茎叶图知,东城区的平均分为
西城区的平均分为,
∴东城区的平均分较高.………………………………………………………(5分)
(2)从两个区域各选一个优秀厂家,所有的基本事件数为种,
满足得分差距不超过5分的事件:
9种,
∴满足条件的概率为…………………………………………………………(12分)
【思路点拨】(1)根据平均数得定义求得东、西两个城区厂家的平均分;(2)用列举法写出
从两个区域各选一个优秀厂家的所有情况共15种,其中满足得分差距不超过5分的情况有9种,所以满足条件的概率为.
【题文】17.(本小题满分12分)
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE=,平面ABCD⊥平面ABE.
(1)求证:平面ADE⊥平面BCE;
(2)求三棱锥D—ACE的体积.
【知识点】线面垂直的判定;锥体的体积公式. G5 G1
【答案】【解析】(1)证明:见解析;(2)解析:(1)∵四边形ABCD是正方形,
∴AD⊥AB.又∵平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,AD平面ABCD,
∴AD⊥平面ABE,而BE平面ABE,∴AD⊥BE.
又∵AE=BE=,AB=2,∴,∴AE⊥BE.
而AD∩AE=A,AD、AE平面ADE,∴BE⊥平面ADE,而BE平面BCE,
∴平面ADE⊥平面BCE.……………………………………………(6分)
(2)取AB的中点O,连接OE,∵△ABE是等腰三角形,∴OE⊥AB.
又∵AD⊥平面ABE,OE平面ABE,∴AD⊥OE,∴OE⊥平面ABCD,
即OE是三棱锥D—ACE的高.又∵AB=AE=BE=2,∴OE=1,
∴.--------(12分)
【思路点拨】(1)根据线面垂直的判定定理,只需在平面BCE内找到直线与平面ADE垂直即可,易知此直线是BE;(2)利用等体积转化法,转化为求三棱锥E-ACD的体积即可.
【题文】18.(本小题满分12分)
设记
(1)求函数的最小正周期;
(2)试用“五点法”画出函数在区间的简图,并指出该函数的图象可由的图象经过怎样的平移和伸缩变换得到;
(3)若时,函数的最小值为2,试求出函数的最大值并指出x取何值时,函数取得最大值.
【知识点】 向量的数量积;二倍角公式;两角和与差的三角函数;函数的图像与性质;F3 C6 C5 C4
【答案】【解析】(1);(2)见解析;(2)时取得最大,最大值为
解析:(1)
, ∴………………………………(3分)
(2)
x
0
0
1
0
-1
0
y
向左平移得到,再保持纵坐标不变,横坐标缩短为原的变为,最后再向上平移个单位得到.……………(8分)
(3)
当即时取得最大,最大值为………………………………(12分)
【思路点拨】(1)利用向量数量积得坐标公式,二倍角公式,两角和与差的三角函数公式,求得,从而得函数的最小正周期;(2)计算时的范围,从而确定“五点法”中的关键点,然后列表、描点、画出图像;可以将
的图像先平移再横伸缩变换得y图像.也可以先进行横伸缩变换再 进行平移变换得y图像;(3)先计算时的范围,
从而得最值关于m的表达式,进而求得结论.
【题文】19.(本小题满分13分)
已知等差数列满足.
(1)求的通项公式; (2)若,数列满足关系式
求证:数列的通项公式为
(3)设(2)中的数列的前项和Sn,对任意的正整数n,
恒成立,求实数p的取值范围.
【知识点】等差数列;已知递推公式求通项;不等式恒成立问题. D2 D1 E8
【答案】【解析】(1)(2)证明:见解析;(3).
解析:(1)设等差数列的公差为d,由已知,有解得
所以即等差数列的通项公式为(3分)
(2)因为所以当时,.
证:当时,,所以
将这n-1个式子相加,得即.
当n=1时,也满足上式.
所以数列的通项公式为.……………………………………(7分)
(3)由(2),所以
所以原不等式变为即
所以对任意恒成立,所以
所以p的取值范围是.……………………………………………………(13分)
【思路点拨】(1)利用已知求得首项和公差即可;(2)累加法证明结论;(3)由(2)中结论化简恒成立的不等式,即对任意恒成立,而,所以
【题文】20.(本小题满分13分)
已知椭圆以坐标原点为中心,坐标轴为对称轴,且椭圆以抛物线y2 =16x的焦点为其一个焦点,以双曲线的焦点为顶点.
(1)求椭圆的标准方程;
(2)已知点A(-1,0),B(1,0),且C,D分别为椭圆的上顶点和右顶点,点P是线段CD上的动点,求的取值范围;
(3)试问在圆上是否存在一点M,使△F1MF2的面积(其中a为椭圆的半长轴长,b为椭圆的半短轴长,F1,F2为椭圆的两个焦点),若存在,求的值;若不存在,请说明理由.
【知识点】 椭圆的方程;向量数量积坐标运算;三角形的面积公式. H5 F3
【答案】【解析】(1);(2);(3)存在点M且=2.
解析:(1)因为抛物线y2=16x的焦点坐标和双曲线的焦点分别为(4,0)和(5,0).
所以所以椭圆的标准方程:.…………………………(3分)
(2)设,则
则当OP⊥CD时,取到最小值,即:
当点P在D点时,取到最大值:OD=5.所以:.……………(7分)
(3)如图所示:
由第一问可知,圆的方程为.△F1MF2的面积
设M(x,y),又△F1MF2的面积
又F1(-4,0),F2(4,0),设直线MF2的倾斜角为,直线MF1的倾斜角为,则
即的值为2.………………………………………………………………(13分)
【思路点拨】(1)由已知得椭圆中的参数a,b,c的值即可;(2)求得线段CD方程
,设出点得向量坐标,从而得
,再化为关于的函数,由得的取值范围;
(3)由(1)得出圆的方程为.△F1MF2的面积不妨设M在x轴上方,结合图形可得点M的纵坐标,进一步求得的三角函数值.
【题文】21.(本小题满分13分)
已知函数
(1)当a=0时,求的极值;
(2)当a<0时,求的单调区间;
(3)若对任意当及,恒有成立,求实数m的取值范围.
【知识点】 导数的应用;不等式恒成立问题. B12 E8
【答案】【解析】(1)的极小值为无极大值;(2)当时,的递减区间为和,递增区间为;当时,在上单调递减;当时,的递减区间为和,递增区间为;
(3)
解析:(1)依题意知的定义域为,
当时,
令,解得当时,;当时,.
又∵∴的极小值为无极大值.………………(3分)
(2)
当时,令得或,
令得当时,得
令得,令得
当时,
综上所述,当时,的递减区间为和,递增区间为;
当时,在上单调递减;
当时,的递减区间为和,递增区间为.…(8分)
(3)由(2)可知,当时,在区间上单调递减;
当x=1时,取得最大值;当x=3时,取得最小值;
恒成立,
,整理得,
恒成立,
………………………………………………………………(13分)
【思路点拨】(1)通过判断导函数为零的点两侧,导函数值的符号,确定极值情况;
(2)通过对a取值的讨论,确定:导函数大于零的x范围是增区间,导函数小于零的范围是减区间;(3)由(2)的结论,化简恒成立的不等式为:,
恒成立,由此求得实数m的取值范围.
【典例剖析】本题第(3)小问是不等式恒成立问题,虽然是常见题型,但本题有一定难度.
需要利用第(2)小问的结论求在上的最大值,从而转化为常规的恒成立问题求解.
同课章节目录
