18.3 一次函数的图像和性质[下]
文档属性
| 名称 | 18.3 一次函数的图像和性质[下] |

|
|
| 格式 | rar | ||
| 文件大小 | 412.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-05 11:58:00 | ||
图片预览






文档简介
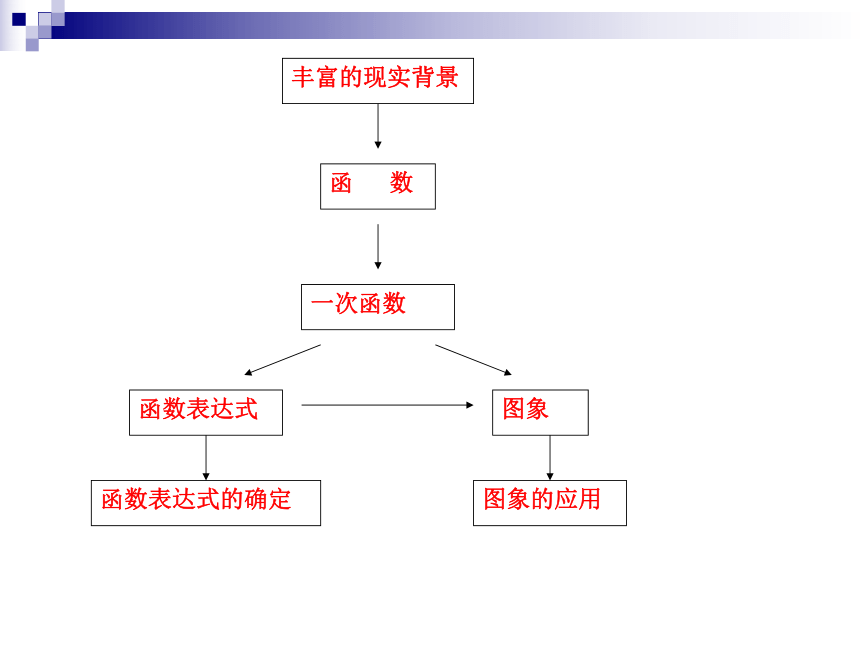
课件18张PPT。第五章 回顾与思考1、函数的定义:
一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定另一个变量y的值,那么我们称y是x的函数,其中x是自变量,y是因变量。 2、一次函数,正比例函数的及联系
两个变量x、y间的关系式可以表示成 ( k≠0,k、b常数)的形式,则称称y是x的一次函数。
当b=0, 时,称y是x的正比例函数。3、函数图象的概念:
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它们的对应点,所有这些点组成的图形叫做该函数的图象。4、一次函数 ( k≠0, b≠0)图象的特征与性质:
(1)一次函数的图象是过(0,b)、( ,0)两点的一条直线;
(2)当k>0时,y随x的增大而增大,k值越大,函数图象与x轴正半轴所成的锐角越大;当k<0时,y随x的增大而减小 正比例函数 图象的特征与性质:
1、正比例函数图象都是过原点(0,0)和(1,k)的一条直线;
2、当k>0时,y随x的增大而增大,k值越大,函数图象与x轴正半轴所成的锐角越大;当k<0时,y随x的增大而减小。5、确定一次函数表达式
①通过观察图象或由条件确定其是正比例函数还是一次函数,然后设其表达式为
或 。
②把已知点的坐标代入,若是正比例函数则需要一个点,若是一次函数,则需要二个点,组成关于k、b的一个或两个方程。
③解方程(组)得k、b的值。
④把k、b代回代到表达式中,得到明朗化的解析式。6、一次函数图象的应用
函数是研究现实世界变化规律的一个重要模型,一次函数是最简单的函数,一次函数的应用十分广泛,它的表示方式有三种,即图象法,表格法,代数表达式法,而且它们之间可以互相转化。[例1] 下面有三个关系式和三个图象,哪一个关系式与哪一个图象能够表示同一个一次函数?
(1) (2) (3)[例2] 已知y是x的一次函数,(1)根据下表写出函数表达式(2)补全下表;(3)作出这个一次函数的图象,并回答下列问题
①随着x值的增大,y值的变化情况是 。
②图象与y轴的交点坐标为 ,与x轴的交点坐标为 。
③当x 时,y≤0[例4] 一农民带了若干斤自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?复习复习,准备考试课外作业:复习参考题
一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定另一个变量y的值,那么我们称y是x的函数,其中x是自变量,y是因变量。 2、一次函数,正比例函数的及联系
两个变量x、y间的关系式可以表示成 ( k≠0,k、b常数)的形式,则称称y是x的一次函数。
当b=0, 时,称y是x的正比例函数。3、函数图象的概念:
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它们的对应点,所有这些点组成的图形叫做该函数的图象。4、一次函数 ( k≠0, b≠0)图象的特征与性质:
(1)一次函数的图象是过(0,b)、( ,0)两点的一条直线;
(2)当k>0时,y随x的增大而增大,k值越大,函数图象与x轴正半轴所成的锐角越大;当k<0时,y随x的增大而减小 正比例函数 图象的特征与性质:
1、正比例函数图象都是过原点(0,0)和(1,k)的一条直线;
2、当k>0时,y随x的增大而增大,k值越大,函数图象与x轴正半轴所成的锐角越大;当k<0时,y随x的增大而减小。5、确定一次函数表达式
①通过观察图象或由条件确定其是正比例函数还是一次函数,然后设其表达式为
或 。
②把已知点的坐标代入,若是正比例函数则需要一个点,若是一次函数,则需要二个点,组成关于k、b的一个或两个方程。
③解方程(组)得k、b的值。
④把k、b代回代到表达式中,得到明朗化的解析式。6、一次函数图象的应用
函数是研究现实世界变化规律的一个重要模型,一次函数是最简单的函数,一次函数的应用十分广泛,它的表示方式有三种,即图象法,表格法,代数表达式法,而且它们之间可以互相转化。[例1] 下面有三个关系式和三个图象,哪一个关系式与哪一个图象能够表示同一个一次函数?
(1) (2) (3)[例2] 已知y是x的一次函数,(1)根据下表写出函数表达式(2)补全下表;(3)作出这个一次函数的图象,并回答下列问题
①随着x值的增大,y值的变化情况是 。
②图象与y轴的交点坐标为 ,与x轴的交点坐标为 。
③当x 时,y≤0[例4] 一农民带了若干斤自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?复习复习,准备考试课外作业:复习参考题
