人教版八年级数学上册12.3角的平分线的性质教学设计
文档属性
| 名称 | 人教版八年级数学上册12.3角的平分线的性质教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 194.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 21:09:27 | ||
图片预览


文档简介
12.3角的平分线的性质教学设计
教学目标:
1.会用尺规作一个角的平分线,知道作法的合理性.
2.探索并证明角的平分线的性质,并能用角的平分线的性质解决简单问题.
3.在探索角的平分线的性质的过程中,体会感性认识与理性认识之间的联系与区别,使学生关注数学。
教学重点:
理解角平分线的性质
教学难点:
灵活运用角的平分线的性质
教学过程:
一、情境诱导
1、在练习本上画一个角,怎样得到这个角的平分线?在生产生活中,这些方法是否可行呢?
2、如图,是一个平分角的仪器,其中AB=AD,BC=DC。将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
3、从利用平分角的仪器画角的平分线中,你受到启发,如何利用直尺和圆规作一个角的平分线?角平分线有什么性质呢?
二、探究指导
请学生逐个思考探究提纲中的问题,老师先作必要的板书准备,再到学生中巡视指导。
探究提纲:
1、画一画:
(1)任意画一个角∠AOB;
(2)用尺规作图作出∠AOB的平分线OC;
(3)在OC 上任取一点P,过点P 画出OA,OB 的垂线,分别记垂足为D,E.
2、量一量:测量线段PD和PE长度, 并作比较.
3、猜一猜:通过测量、比较,你能得到什么结论?
4、证一证:试把你发现的结论改写成已知、求证并证明.
三、展示归纳
请学生逐个展示探究提纲中问题,发动学生评价,老师作以补充完善,并对重点内容作以强调。
四、变式练习
逐题出示,先让学生独立完成,再请有问题的学生汇报结果,老师板书,并发动其他学生评价、补充并完善,最后老师根据需要进行重点强调。
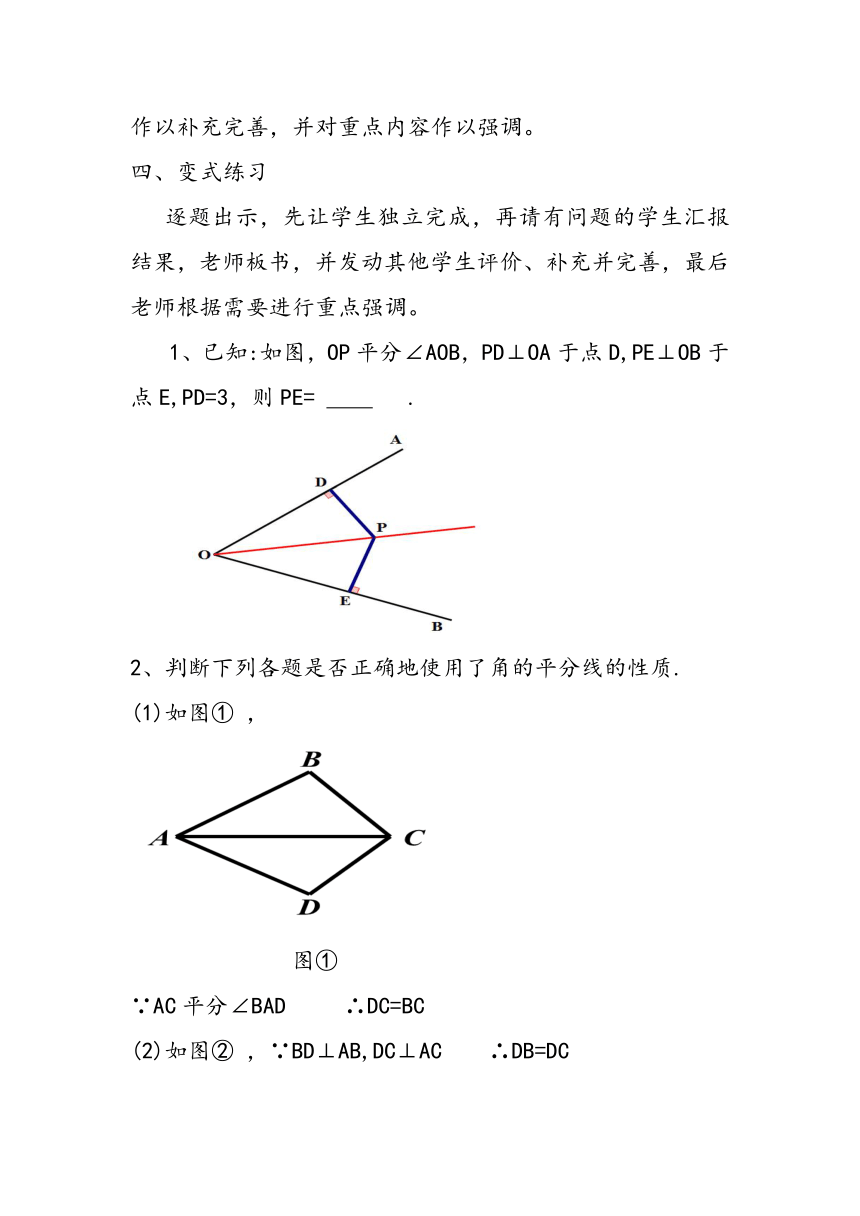
1、已知:如图,OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E,PD=3,则PE= .
2、判断下列各题是否正确地使用了角的平分线的性质.
(1)如图① ,
图①
∵AC平分∠BAD ∴DC=BC
(2)如图② ,∵BD⊥AB,DC⊥AC ∴DB=DC
图②
(3)如图②,∵AD平分∠BAC 且DB⊥AB,DC⊥AC ∴BD=CD
2、 如图,△ABC中,∠B =∠C,AD 是∠BAC 的平分线, DE⊥AB,DF⊥AC,垂足分别为E,F.
求证:EB =FC.
3、如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长?
4、 如图,△ABC 的角平分线BM,CN 相交于点P.
求证:点P到三边AB,BC,CA 的距离相等.
五、课堂小结
通过本节课的学习你学会了哪些知识 (先请学生进行自主小结,再由老师概括总结,形成知识体系)
六、作业
必做:教科书习题12.3第1、2题.
选做:教科书习题12.3第4题.
七、反思
在课堂上,要充分利用教材这个主要教学资源。通过学生阅读教材,探讨解题思路,知识形成过程和结构特点过程中就对知识有了一个比较清晰的轮廓;而对有难度的地方,教师就去引导学生复习旧知,自然的就迁移到新知识之中去了,从而帮助学生形成了自己独特的学习方法。引导学生动手实践释疑。“动手实践”源于生活数学化,数学生活化的内涵。在课堂中,对于比较抽象、深奥的数学,需要让学生去想象感知,所以动手去做尤为关键。
本节课通过学生课堂练习,及课后作业的完成情况,大部分同学已基本掌角平分线的性质,并能做简单的运用角的平分线的性质进行一些简单的变式练习。学生总体情况掌握较好,课堂上学生回答问题积极踊跃,
数学是生活、劳动和学习必不可少的工具。数学来源于生活,数学教学的最终目的是让学生在生活中用数学,所以,在数学教学中,必须加强数学与生活的联系,从而提高学生数学素养。
教学目标:
1.会用尺规作一个角的平分线,知道作法的合理性.
2.探索并证明角的平分线的性质,并能用角的平分线的性质解决简单问题.
3.在探索角的平分线的性质的过程中,体会感性认识与理性认识之间的联系与区别,使学生关注数学。
教学重点:
理解角平分线的性质
教学难点:
灵活运用角的平分线的性质
教学过程:
一、情境诱导
1、在练习本上画一个角,怎样得到这个角的平分线?在生产生活中,这些方法是否可行呢?
2、如图,是一个平分角的仪器,其中AB=AD,BC=DC。将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
3、从利用平分角的仪器画角的平分线中,你受到启发,如何利用直尺和圆规作一个角的平分线?角平分线有什么性质呢?
二、探究指导
请学生逐个思考探究提纲中的问题,老师先作必要的板书准备,再到学生中巡视指导。
探究提纲:
1、画一画:
(1)任意画一个角∠AOB;
(2)用尺规作图作出∠AOB的平分线OC;
(3)在OC 上任取一点P,过点P 画出OA,OB 的垂线,分别记垂足为D,E.
2、量一量:测量线段PD和PE长度, 并作比较.
3、猜一猜:通过测量、比较,你能得到什么结论?
4、证一证:试把你发现的结论改写成已知、求证并证明.
三、展示归纳
请学生逐个展示探究提纲中问题,发动学生评价,老师作以补充完善,并对重点内容作以强调。
四、变式练习
逐题出示,先让学生独立完成,再请有问题的学生汇报结果,老师板书,并发动其他学生评价、补充并完善,最后老师根据需要进行重点强调。
1、已知:如图,OP平分∠AOB,PD⊥OA于点D,PE⊥OB于点E,PD=3,则PE= .
2、判断下列各题是否正确地使用了角的平分线的性质.
(1)如图① ,
图①
∵AC平分∠BAD ∴DC=BC
(2)如图② ,∵BD⊥AB,DC⊥AC ∴DB=DC
图②
(3)如图②,∵AD平分∠BAC 且DB⊥AB,DC⊥AC ∴BD=CD
2、 如图,△ABC中,∠B =∠C,AD 是∠BAC 的平分线, DE⊥AB,DF⊥AC,垂足分别为E,F.
求证:EB =FC.
3、如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长?
4、 如图,△ABC 的角平分线BM,CN 相交于点P.
求证:点P到三边AB,BC,CA 的距离相等.
五、课堂小结
通过本节课的学习你学会了哪些知识 (先请学生进行自主小结,再由老师概括总结,形成知识体系)
六、作业
必做:教科书习题12.3第1、2题.
选做:教科书习题12.3第4题.
七、反思
在课堂上,要充分利用教材这个主要教学资源。通过学生阅读教材,探讨解题思路,知识形成过程和结构特点过程中就对知识有了一个比较清晰的轮廓;而对有难度的地方,教师就去引导学生复习旧知,自然的就迁移到新知识之中去了,从而帮助学生形成了自己独特的学习方法。引导学生动手实践释疑。“动手实践”源于生活数学化,数学生活化的内涵。在课堂中,对于比较抽象、深奥的数学,需要让学生去想象感知,所以动手去做尤为关键。
本节课通过学生课堂练习,及课后作业的完成情况,大部分同学已基本掌角平分线的性质,并能做简单的运用角的平分线的性质进行一些简单的变式练习。学生总体情况掌握较好,课堂上学生回答问题积极踊跃,
数学是生活、劳动和学习必不可少的工具。数学来源于生活,数学教学的最终目的是让学生在生活中用数学,所以,在数学教学中,必须加强数学与生活的联系,从而提高学生数学素养。
