2023—2024学年人教版数学七年级上册 1.2.4 绝对值课件 18张PPT
文档属性
| 名称 | 2023—2024学年人教版数学七年级上册 1.2.4 绝对值课件 18张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 21:25:29 | ||
图片预览





文档简介
(共18张PPT)
1.2.4.1 绝对值
人教版 七年级上
第一章 有理数
1、理解绝对值的概念及其几何意义,通过从数形两个方面理解绝对值的意义,初步了解数形结合的思想方法。
2、会求一个数的绝对值,知道一个数的绝对值,会求这个数。
3、掌握绝对值的有关性质。
4、通过应用绝对值解决实际问题,培养学生深厚的学习兴趣,提高学生学数学的好奇心和求知欲。
学习目标
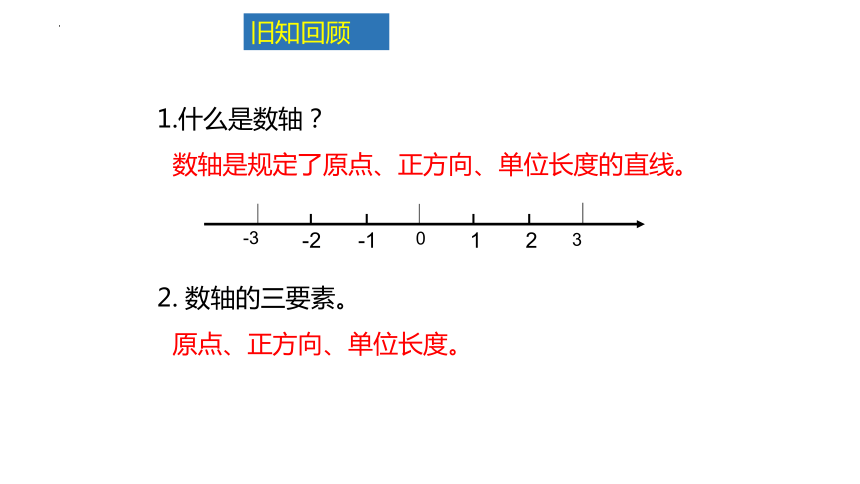
1.什么是数轴?
旧知回顾
数轴是规定了原点、正方向、单位长度的直线。
0
3
-3
1
2
-2
-1
2. 数轴的三要素。
原点、正方向、单位长度。
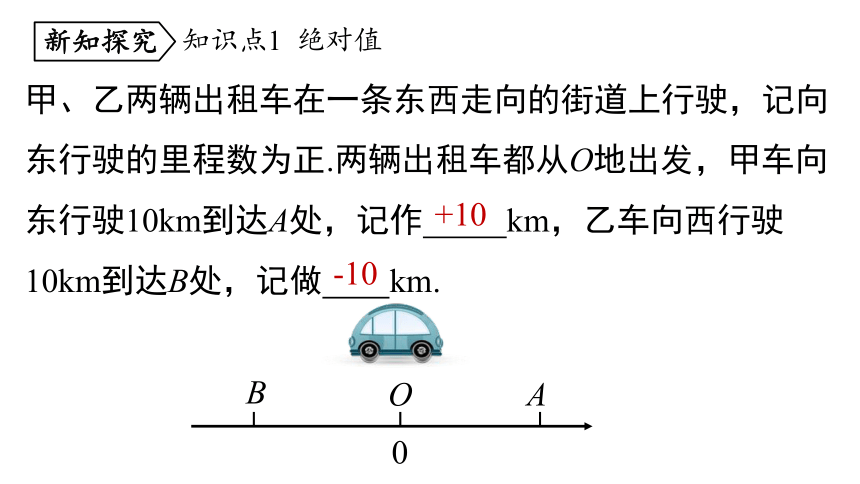
甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作 km,乙车向西行驶10km到达B处,记做 km.
+10
-10
0
O
B
A
知识点1 绝对值
新知探究
绝对值:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a| .
(这里的数a可以是正数、负数和0).
注意:任何数都有绝对值,并且只有一个,数a的绝对值,是表示它的点到原点的距离.因为距离不可能是负数,所以数a的绝对值为非负数,即|a|≥0.
知识点:绝对值的代数意义
获取新知
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
0的绝对值是0;
用式子表示为:
小组讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有 ≥0
1. 绝对值是7的数有几个?各是什么?有没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7. 没有绝对值是-2的数.
2.绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,是0.
3.绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个, 它们分别是-2,-1,0,1,2.
1.写出下列各数的绝对值:
9,-10,-7.9,,-,120,0
|9|=9 |-10|=10 |-7.9|=7.9
||=|-|=|-| |120|=120 |0|=0
解:
2.-2的绝对值是____,说明数轴上表示-2 的点到____的距离是____个长度单位.
3.-0.8的绝对值是____ .
4.口答:|+6 |= | |= | 8.2 |=
| 0 |= | -3 |= | |=
2
2
0.8
6
0
8.2
3
原点
例1 写出下列各数的绝对值:
6,-8,-3.9, , ,100, 0.
巩固应用
它们的绝对值分别是:
6,8,3.9, , ,100,0.
例2 判断下列说法是否正确:
(1)符号相反的数互为相反数;
(2)一个数的绝对值越大,表示它的点在数轴上越靠右;
(3)一个数的绝对值越大,表示它的点在数轴上离原点越远;
(4)当 时, 总是大于0.
巩固应用
不正确
不正确
正确
正确
例3 判断下列各式是否正确:
(1)
(2)
(3)
巩固应用
正确
不正确
不正确
例4 化简:
(1) ;(2)
巩固应用
(1)
(2)
例5(1)如果 2,那么 = .
(2)如果 0,那么 = .
(3)如果 ,那么 0.
(4)如果 - ,那么 0.
(5)如果 ,那么 = .
巩固应用
±2
0
≥
≤
0
拓展提高
例6 已知数轴上有A和B两点,它们之间的距离为1,点A和原点的距离为2,那么所有满足条件的点B对应的数是________
B:1或3;-1或-3
A:2或-2
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
课堂小结
一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
1.2.4.1 绝对值
人教版 七年级上
第一章 有理数
1、理解绝对值的概念及其几何意义,通过从数形两个方面理解绝对值的意义,初步了解数形结合的思想方法。
2、会求一个数的绝对值,知道一个数的绝对值,会求这个数。
3、掌握绝对值的有关性质。
4、通过应用绝对值解决实际问题,培养学生深厚的学习兴趣,提高学生学数学的好奇心和求知欲。
学习目标
1.什么是数轴?
旧知回顾
数轴是规定了原点、正方向、单位长度的直线。
0
3
-3
1
2
-2
-1
2. 数轴的三要素。
原点、正方向、单位长度。
甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作 km,乙车向西行驶10km到达B处,记做 km.
+10
-10
0
O
B
A
知识点1 绝对值
新知探究
绝对值:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a| .
(这里的数a可以是正数、负数和0).
注意:任何数都有绝对值,并且只有一个,数a的绝对值,是表示它的点到原点的距离.因为距离不可能是负数,所以数a的绝对值为非负数,即|a|≥0.
知识点:绝对值的代数意义
获取新知
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
0的绝对值是0;
用式子表示为:
小组讨论下面3个问题:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有 ≥0
1. 绝对值是7的数有几个?各是什么?有没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7. 没有绝对值是-2的数.
2.绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,是0.
3.绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个, 它们分别是-2,-1,0,1,2.
1.写出下列各数的绝对值:
9,-10,-7.9,,-,120,0
|9|=9 |-10|=10 |-7.9|=7.9
||=|-|=|-| |120|=120 |0|=0
解:
2.-2的绝对值是____,说明数轴上表示-2 的点到____的距离是____个长度单位.
3.-0.8的绝对值是____ .
4.口答:|+6 |= | |= | 8.2 |=
| 0 |= | -3 |= | |=
2
2
0.8
6
0
8.2
3
原点
例1 写出下列各数的绝对值:
6,-8,-3.9, , ,100, 0.
巩固应用
它们的绝对值分别是:
6,8,3.9, , ,100,0.
例2 判断下列说法是否正确:
(1)符号相反的数互为相反数;
(2)一个数的绝对值越大,表示它的点在数轴上越靠右;
(3)一个数的绝对值越大,表示它的点在数轴上离原点越远;
(4)当 时, 总是大于0.
巩固应用
不正确
不正确
正确
正确
例3 判断下列各式是否正确:
(1)
(2)
(3)
巩固应用
正确
不正确
不正确
例4 化简:
(1) ;(2)
巩固应用
(1)
(2)
例5(1)如果 2,那么 = .
(2)如果 0,那么 = .
(3)如果 ,那么 0.
(4)如果 - ,那么 0.
(5)如果 ,那么 = .
巩固应用
±2
0
≥
≤
0
拓展提高
例6 已知数轴上有A和B两点,它们之间的距离为1,点A和原点的距离为2,那么所有满足条件的点B对应的数是________
B:1或3;-1或-3
A:2或-2
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
课堂小结
一个正数的绝对值是它本身.
一个负数的绝对值是它的相反数.
0的绝对值是0.
