山东省威海市威海经济技术开发区2022-2023学年七年级下学期期末数学试题(含答案)
文档属性
| 名称 | 山东省威海市威海经济技术开发区2022-2023学年七年级下学期期末数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 604.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 17:31:27 | ||
图片预览


文档简介
2022~2023学年度第二学期质量检测
初二数学
注意事项:
1.本次考试时间120分钟,满分120分.
2.答题时,请务必在题号所指示的区域内作答,作图用2B铅笔.
3.不要求保留精确度的题目,计算结果保留准确值,祝考试成功!
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分)
1.下列方程组中,是二元一次方程组的是( )
A. B. C. D.
2.将只有颜色不同的3个白球、2个黑球放在一个不透明的布袋中,下列四个选项,不正确的是( )
A.从布袋中任意摸出1个球,摸出的球是黑球,该事件是一个随机本件;
B.从布袋中任意摸出1个球,摸出的球是红球,该事件是一个确定事件;
C.从布袋中任意拱出1个球,摸出的球是墨球或白球,该事件是一个确定事件;
D.从布袋中任意摸出3个球,其中有一个球是白球,该事件是一个随机事件。
3.下列说法不一定成立的是( )
A.若,则; B.若,则;
C.若,则; D.若,则.
4.下列命题中,是假命题的是( )
A.平面内点与点关于轴对称;
B.如果两条直线被第三条直线所伐得的内错角相等,则同位角也相等;
C.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行:
D.在同一平面内,过一点有且只有一条直线与已知直线垂直.
5.质检人员从编号为1,2,3,4,5的五种不同产品中随机抽取一种进行质量检测,所抽到的产品编号不小于4的概率为( )
А. B. C. D.
6.如图,已知,直线与直线分别交于点,分别以点为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交直线b于点,连接,若,则的度数是( )
A. B. C. D.
7.我国古代数学名著《算法统宗》中记载:“今有绫七尺,罗九尺,共价适等;只云罗每尺价比绫每尺少线三十六文,问各钱价若干?”意思是:现在有一匹7尺长的绫布和一匹9尺长的罗布恰好一样贵,只知道每尺罗布比绫布便宜36文,问两种布每尺各多少钱?设绫布每尺文,罗布每尺文,那么可列方程组为( )
A. B. C. D.
8.若不等式组有解,则的取值范围为( )
A. B. C. D.
9.“三等分角”大约是在公元前五世纪由古希腊人提出来的.如图所示的“三等分角仪”能三等分任一角,它由两根有槽的棒组成,两根棒在点相连并可绕转动,点固定,,点可在槽中滑动,若,则的度数是( )
A. B. C. D.
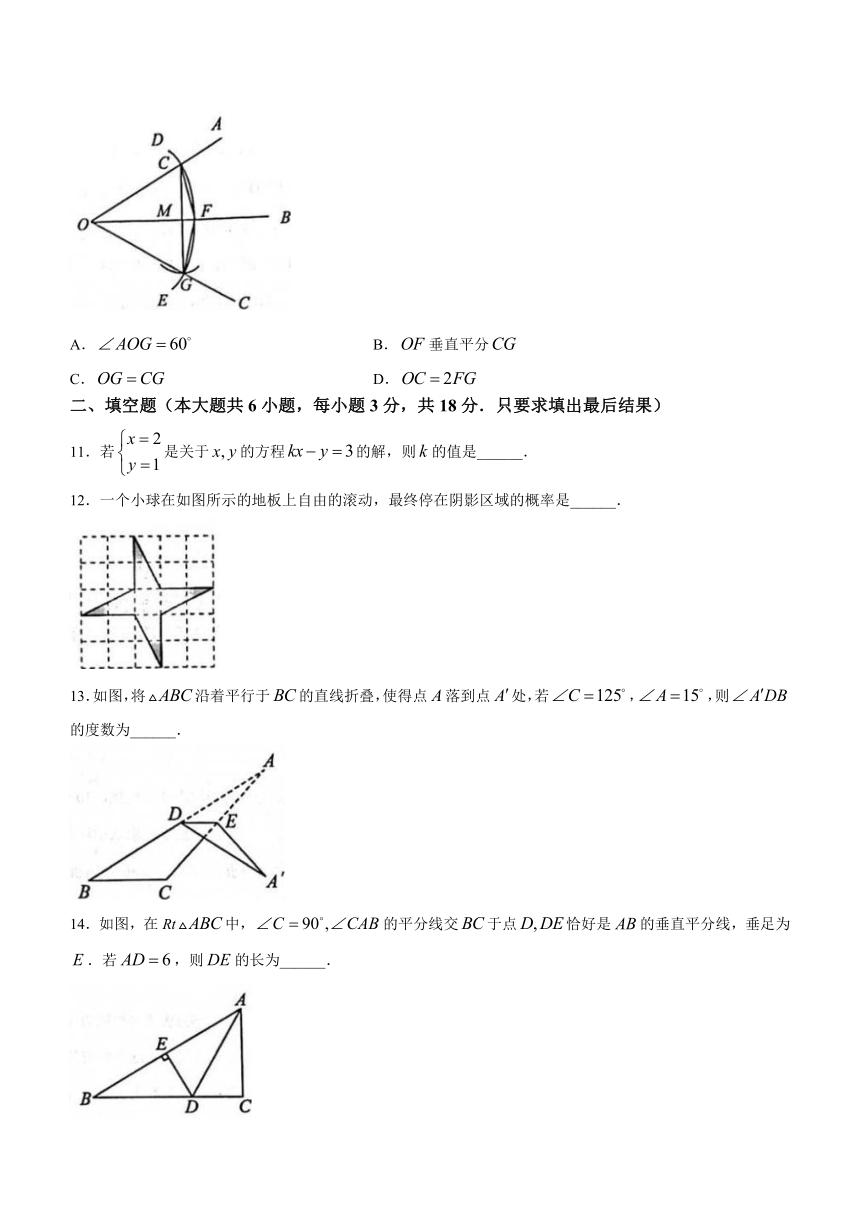
10.如图,.按下列步骤作图:
①在射线OA上取一点C,以点O为圆心,OC长为半径作圆弧DE,交射线OB于点F.连结CF;
②以点F为圆心,CF长为半径作圆弧,交弧DE于点G;
③连结FG、CG.作射线OG.
根据以上作图过程及所作图形,下列结论中错误的是( )
A. B.垂直平分
C. D.
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
11.若是关于的方程的解,则的值是______.
12.一个小球在如图所示的地板上自由的滚动,最终停在阴影区域的概率是______.
13.如图,将沿着平行于的直线折叠,使得点落到点处,若,,则的度数为______.
14.如图,在Rt中,的平分线交于点恰好是的垂直平分线,垂足为.若,则的长为______.
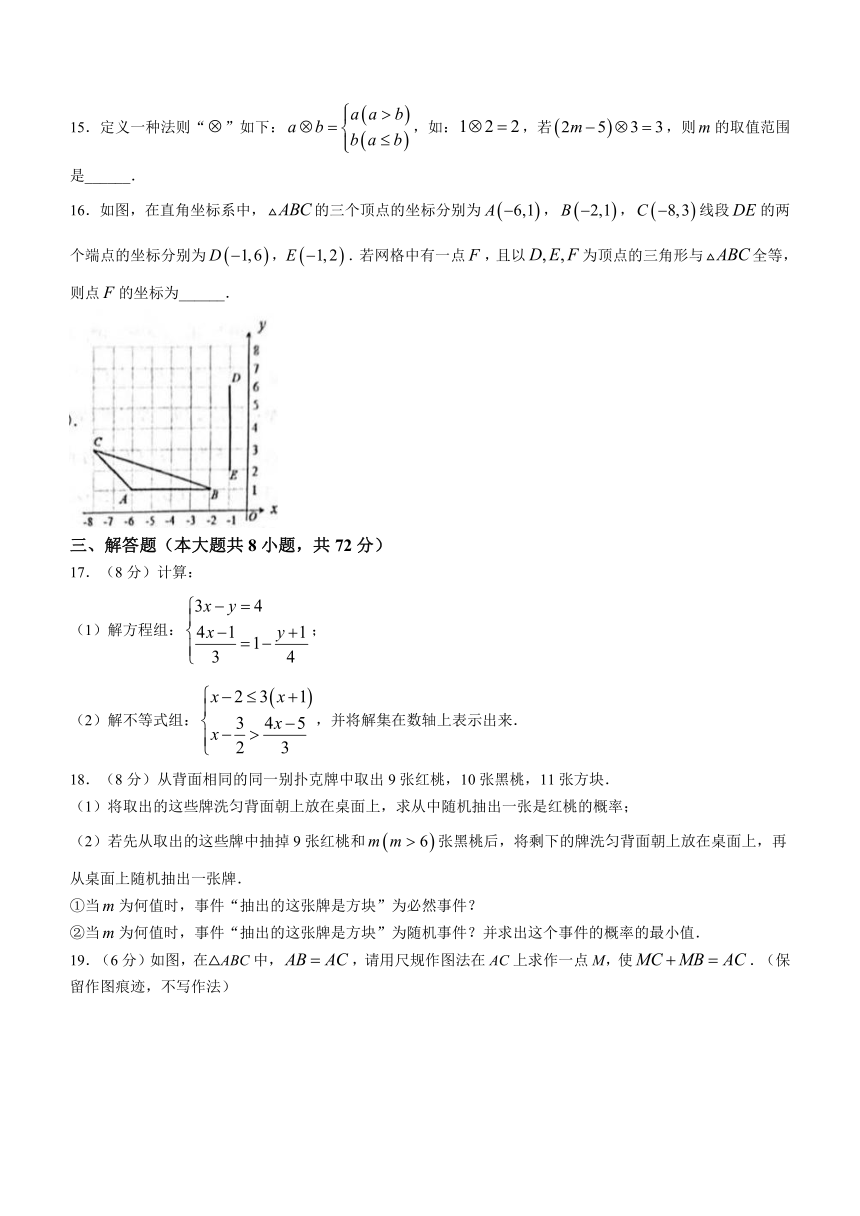
15.定义一种法则“”如下:,如:,若,则的取值范围是______.
16.如图,在直角坐标系中,的三个顶点的坐标分别为,,线段的两个端点的坐标分别为,.若网格中有一点,且以为顶点的三角形与全等,则点的坐标为______.
三、解答题(本大题共8小题,共72分)
17.(8分)计算:
(1)解方程组:;
(2)解不等式组:,并将解集在数轴上表示出来.
18.(8分)从背面相同的同一别扑克牌中取出9张红桃,10张黑桃,11张方块.
(1)将取出的这些牌洗匀背面朝上放在桌面上,求从中随机抽出一张是红桃的概率;
(2)若先从取出的这些牌中抽掉9张红桃和张黑桃后,将剩下的牌洗匀背面朝上放在桌面上,再从桌面上随机抽出一张牌.
①当为何值时,事件“抽出的这张牌是方块”为必然事件?
②当为何值时,事件“抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
19.(6分)如图,在△ABC中,,请用尺规作图法在AC上求作一点M,使.(保留作图痕迹,不写作法)
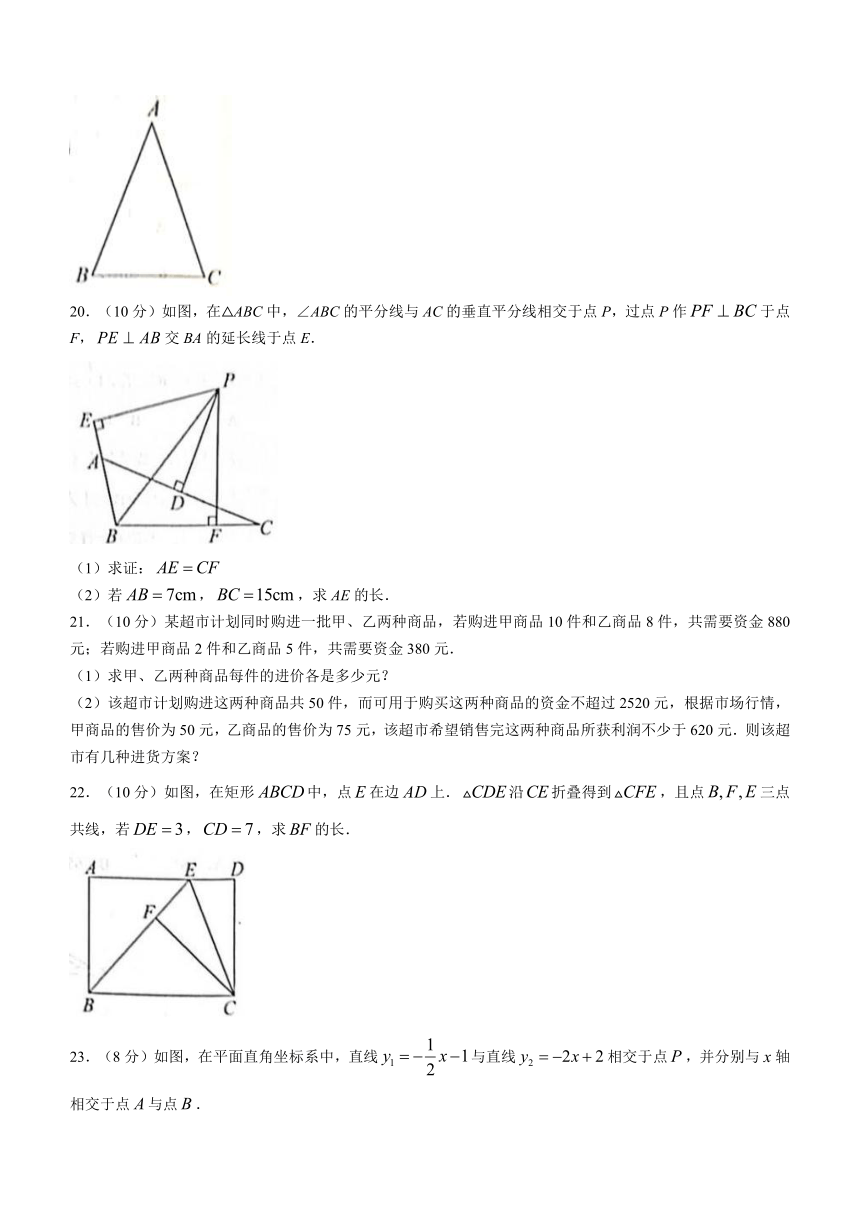
20.(10分)如图,在△ABC中,∠ABC的平分线与AC的垂直平分线相交于点P,过点P作于点F,交BA的延长线于点E.
(1)求证:
(2)若,,求AE的长.
21.(10分)某超市计划同时购进一批甲、乙两种商品,若购进甲商品10件和乙商品8件,共需要资金880元;若购进甲商品2件和乙商品5件,共需要资金380元.
(1)求甲、乙两种商品每件的进价各是多少元?
(2)该超市计划购进这两种商品共50件,而可用于购买这两种商品的资金不超过2520元,根据市场行情,甲商品的售价为50元,乙商品的售价为75元,该超市希望销售完这两种商品所获利润不少于620元.则该超市有几种进货方案?
22.(10分)如图,在矩形中,点在边上.沿折叠得到,且点三点共线,若,,求的长.
23.(8分)如图,在平面直角坐标系中,直线与直线相交于点,并分别与轴相交于点与点.
(1)求的面积;
(2)在直线的图象中,把满足的部分描黑加粗,并直接写出满足条件的自变量的取值范围.
24.(12分)新概念:我们把对角线互相垂直的四边形叫做垂美四边形.
概念理解:如图①,在四边形中,如果,那么四边形是垂美四边形吗?请说明理由.
性质探究:小美同学猜想“垂美四边形两组对边的平方和相等”,即,如图②,在四边形中,与相交于点,若,则.请判断小美同学的猜想是否正确,并说明理由.
问题解决:如图③,分别以Rt的直角边和斜边为边向外作正方形和正方形,连接.若,,则
(1)求证:.
(2)______.
经区初中数学答案(初二)
一、选择(本大题共10小题,每小题3分,共30分)
1.C 2.D 3.C 4.A 5.B 6.C 7.B 8.A 9.D 10.D
二、填空(本大题共6小题,每小题3分,共18分)
11.2 12. 13. 14.3 15. 16.(或
三、解答(66分)
17.(8分)
(1)解:
整理得:
①得,③,②+③得,解得,
将代入①得,,解得,∴方程组的解为:
(2)解:,由①得:,由②得:,
在数轴上表示如图所示:
∴不等式组的解集为
18.(8分)
(1)解:共种等可能的结果,其中随机抽出一张是红桃共有9种等可能的情况∴;
(2)①∵必然事件的概率为1,即剩下的所有的牌均为方块,∴;
②∵“抽出的这张牌是方块”为随机事件,∴剩余的牌中必须要有黑桃,∴,即:,8,9
要使“抽出的这张牌是方块”这个事件的概率的最小,∴抽掉的牌中黑桃最少
∴∴.
19.(6分)
如图,点即为所求.
20.(10分)
(1)证明:如图,连接
∵的平分线与的垂直平分线相交于点,,,∴,,
∵,∴,
∴,∴
(2)解:在Rt和Rt中∵,
∴,∴,∴,
∵,,∴,∴.
21.(10分)
解:(1)设甲商品每件的进价是元,乙商品每件的进价是元,根据题意得,
,解得:,
答:甲商品每件的进价是40元,乙商品每件的进价是60元:
(2)解:设购进甲商品件,则购进乙商品件,根据题意得,
解得:,
∵为正整数,∴,25,26∴有三种进货方案,
22.(10分)
解:∵四边形是矩形,
∴,,
∵沿折叠得到,
∴,
∴,,
∴,,,
∴,∴,∴,
设,则,
在Rt中,由勾股定理得,
解得,即.
23.(8分)
解:(1)根据题意,交点的横、纵坐标是方程组的解
解这个方程组,得∴的坐标为,
∵直线与轴的交点的坐标为
直线与轴交点的坐标为,
∴∴的面积为
(3)的部分描黑加粗,如图所示:
此时自变量的取值范围
24.(12分)
解:概念理解:四边形是垂美四边形.
理由如下:连接
∵,∴点在线段的垂直平分线上,
∵,∴点在线段的垂直平分线上,∴是线段的垂直平分线,
∴,即四边形是垂美四边形.
性质探究:正确.
如图①,已知四边形中,,垂足为,
∵,∴,
由勾股定理得,,,
,,
∴,
;
∴
问题解决:①连接,
∵正方形和正方形
∴,,,
∴,即,
∴;
②;
初二数学
注意事项:
1.本次考试时间120分钟,满分120分.
2.答题时,请务必在题号所指示的区域内作答,作图用2B铅笔.
3.不要求保留精确度的题目,计算结果保留准确值,祝考试成功!
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分)
1.下列方程组中,是二元一次方程组的是( )
A. B. C. D.
2.将只有颜色不同的3个白球、2个黑球放在一个不透明的布袋中,下列四个选项,不正确的是( )
A.从布袋中任意摸出1个球,摸出的球是黑球,该事件是一个随机本件;
B.从布袋中任意摸出1个球,摸出的球是红球,该事件是一个确定事件;
C.从布袋中任意拱出1个球,摸出的球是墨球或白球,该事件是一个确定事件;
D.从布袋中任意摸出3个球,其中有一个球是白球,该事件是一个随机事件。
3.下列说法不一定成立的是( )
A.若,则; B.若,则;
C.若,则; D.若,则.
4.下列命题中,是假命题的是( )
A.平面内点与点关于轴对称;
B.如果两条直线被第三条直线所伐得的内错角相等,则同位角也相等;
C.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行:
D.在同一平面内,过一点有且只有一条直线与已知直线垂直.
5.质检人员从编号为1,2,3,4,5的五种不同产品中随机抽取一种进行质量检测,所抽到的产品编号不小于4的概率为( )
А. B. C. D.
6.如图,已知,直线与直线分别交于点,分别以点为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交直线b于点,连接,若,则的度数是( )
A. B. C. D.
7.我国古代数学名著《算法统宗》中记载:“今有绫七尺,罗九尺,共价适等;只云罗每尺价比绫每尺少线三十六文,问各钱价若干?”意思是:现在有一匹7尺长的绫布和一匹9尺长的罗布恰好一样贵,只知道每尺罗布比绫布便宜36文,问两种布每尺各多少钱?设绫布每尺文,罗布每尺文,那么可列方程组为( )
A. B. C. D.
8.若不等式组有解,则的取值范围为( )
A. B. C. D.
9.“三等分角”大约是在公元前五世纪由古希腊人提出来的.如图所示的“三等分角仪”能三等分任一角,它由两根有槽的棒组成,两根棒在点相连并可绕转动,点固定,,点可在槽中滑动,若,则的度数是( )
A. B. C. D.
10.如图,.按下列步骤作图:
①在射线OA上取一点C,以点O为圆心,OC长为半径作圆弧DE,交射线OB于点F.连结CF;
②以点F为圆心,CF长为半径作圆弧,交弧DE于点G;
③连结FG、CG.作射线OG.
根据以上作图过程及所作图形,下列结论中错误的是( )
A. B.垂直平分
C. D.
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
11.若是关于的方程的解,则的值是______.
12.一个小球在如图所示的地板上自由的滚动,最终停在阴影区域的概率是______.
13.如图,将沿着平行于的直线折叠,使得点落到点处,若,,则的度数为______.
14.如图,在Rt中,的平分线交于点恰好是的垂直平分线,垂足为.若,则的长为______.
15.定义一种法则“”如下:,如:,若,则的取值范围是______.
16.如图,在直角坐标系中,的三个顶点的坐标分别为,,线段的两个端点的坐标分别为,.若网格中有一点,且以为顶点的三角形与全等,则点的坐标为______.
三、解答题(本大题共8小题,共72分)
17.(8分)计算:
(1)解方程组:;
(2)解不等式组:,并将解集在数轴上表示出来.
18.(8分)从背面相同的同一别扑克牌中取出9张红桃,10张黑桃,11张方块.
(1)将取出的这些牌洗匀背面朝上放在桌面上,求从中随机抽出一张是红桃的概率;
(2)若先从取出的这些牌中抽掉9张红桃和张黑桃后,将剩下的牌洗匀背面朝上放在桌面上,再从桌面上随机抽出一张牌.
①当为何值时,事件“抽出的这张牌是方块”为必然事件?
②当为何值时,事件“抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
19.(6分)如图,在△ABC中,,请用尺规作图法在AC上求作一点M,使.(保留作图痕迹,不写作法)
20.(10分)如图,在△ABC中,∠ABC的平分线与AC的垂直平分线相交于点P,过点P作于点F,交BA的延长线于点E.
(1)求证:
(2)若,,求AE的长.
21.(10分)某超市计划同时购进一批甲、乙两种商品,若购进甲商品10件和乙商品8件,共需要资金880元;若购进甲商品2件和乙商品5件,共需要资金380元.
(1)求甲、乙两种商品每件的进价各是多少元?
(2)该超市计划购进这两种商品共50件,而可用于购买这两种商品的资金不超过2520元,根据市场行情,甲商品的售价为50元,乙商品的售价为75元,该超市希望销售完这两种商品所获利润不少于620元.则该超市有几种进货方案?
22.(10分)如图,在矩形中,点在边上.沿折叠得到,且点三点共线,若,,求的长.
23.(8分)如图,在平面直角坐标系中,直线与直线相交于点,并分别与轴相交于点与点.
(1)求的面积;
(2)在直线的图象中,把满足的部分描黑加粗,并直接写出满足条件的自变量的取值范围.
24.(12分)新概念:我们把对角线互相垂直的四边形叫做垂美四边形.
概念理解:如图①,在四边形中,如果,那么四边形是垂美四边形吗?请说明理由.
性质探究:小美同学猜想“垂美四边形两组对边的平方和相等”,即,如图②,在四边形中,与相交于点,若,则.请判断小美同学的猜想是否正确,并说明理由.
问题解决:如图③,分别以Rt的直角边和斜边为边向外作正方形和正方形,连接.若,,则
(1)求证:.
(2)______.
经区初中数学答案(初二)
一、选择(本大题共10小题,每小题3分,共30分)
1.C 2.D 3.C 4.A 5.B 6.C 7.B 8.A 9.D 10.D
二、填空(本大题共6小题,每小题3分,共18分)
11.2 12. 13. 14.3 15. 16.(或
三、解答(66分)
17.(8分)
(1)解:
整理得:
①得,③,②+③得,解得,
将代入①得,,解得,∴方程组的解为:
(2)解:,由①得:,由②得:,
在数轴上表示如图所示:
∴不等式组的解集为
18.(8分)
(1)解:共种等可能的结果,其中随机抽出一张是红桃共有9种等可能的情况∴;
(2)①∵必然事件的概率为1,即剩下的所有的牌均为方块,∴;
②∵“抽出的这张牌是方块”为随机事件,∴剩余的牌中必须要有黑桃,∴,即:,8,9
要使“抽出的这张牌是方块”这个事件的概率的最小,∴抽掉的牌中黑桃最少
∴∴.
19.(6分)
如图,点即为所求.
20.(10分)
(1)证明:如图,连接
∵的平分线与的垂直平分线相交于点,,,∴,,
∵,∴,
∴,∴
(2)解:在Rt和Rt中∵,
∴,∴,∴,
∵,,∴,∴.
21.(10分)
解:(1)设甲商品每件的进价是元,乙商品每件的进价是元,根据题意得,
,解得:,
答:甲商品每件的进价是40元,乙商品每件的进价是60元:
(2)解:设购进甲商品件,则购进乙商品件,根据题意得,
解得:,
∵为正整数,∴,25,26∴有三种进货方案,
22.(10分)
解:∵四边形是矩形,
∴,,
∵沿折叠得到,
∴,
∴,,
∴,,,
∴,∴,∴,
设,则,
在Rt中,由勾股定理得,
解得,即.
23.(8分)
解:(1)根据题意,交点的横、纵坐标是方程组的解
解这个方程组,得∴的坐标为,
∵直线与轴的交点的坐标为
直线与轴交点的坐标为,
∴∴的面积为
(3)的部分描黑加粗,如图所示:
此时自变量的取值范围
24.(12分)
解:概念理解:四边形是垂美四边形.
理由如下:连接
∵,∴点在线段的垂直平分线上,
∵,∴点在线段的垂直平分线上,∴是线段的垂直平分线,
∴,即四边形是垂美四边形.
性质探究:正确.
如图①,已知四边形中,,垂足为,
∵,∴,
由勾股定理得,,,
,,
∴,
;
∴
问题解决:①连接,
∵正方形和正方形
∴,,,
∴,即,
∴;
②;
同课章节目录
