第22章 相似形 单元练习(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第22章 相似形 单元练习 2023-2024学年 沪科版(2012)九年级数学上册 (含解析)
一、单选题
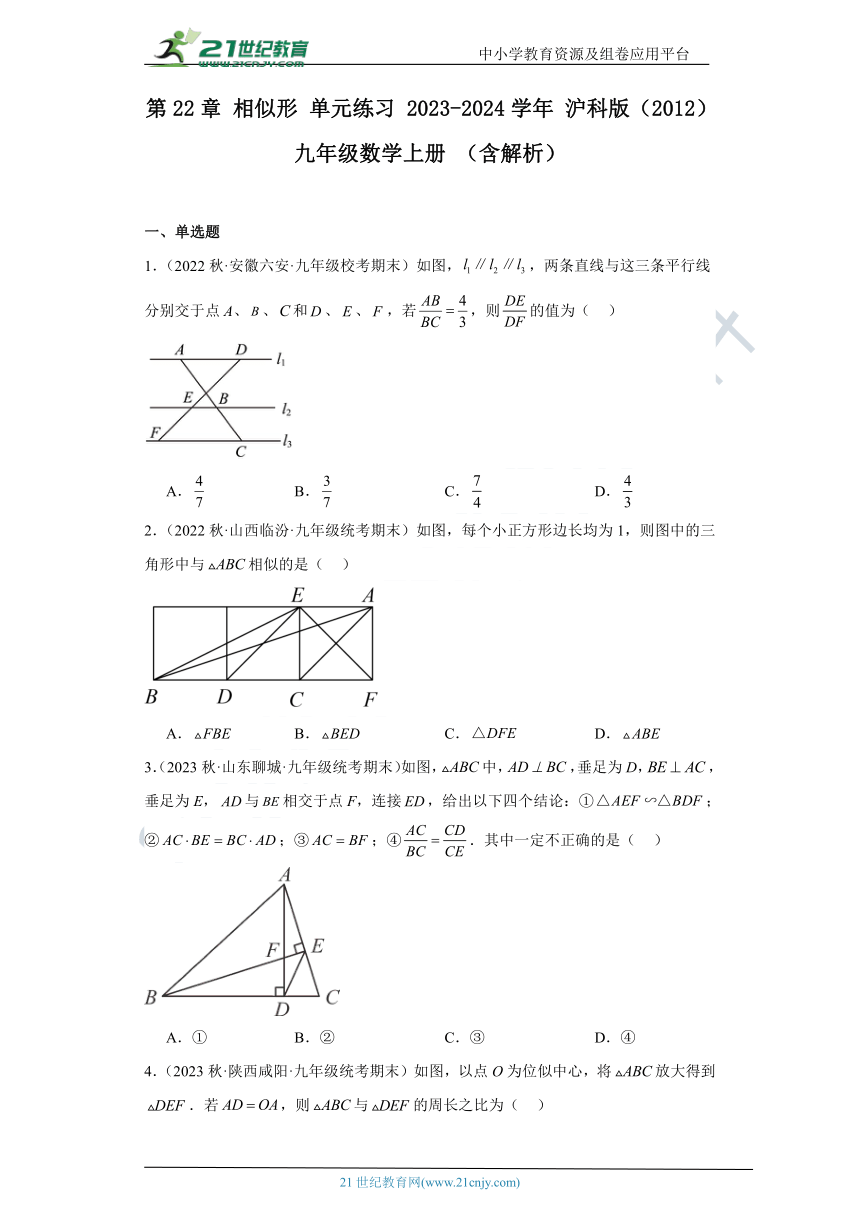
1.(2022秋·安徽六安·九年级校考期末)如图,,两条直线与这三条平行线分别交于点A、、和、、,若,则的值为( )
A. B. C. D.
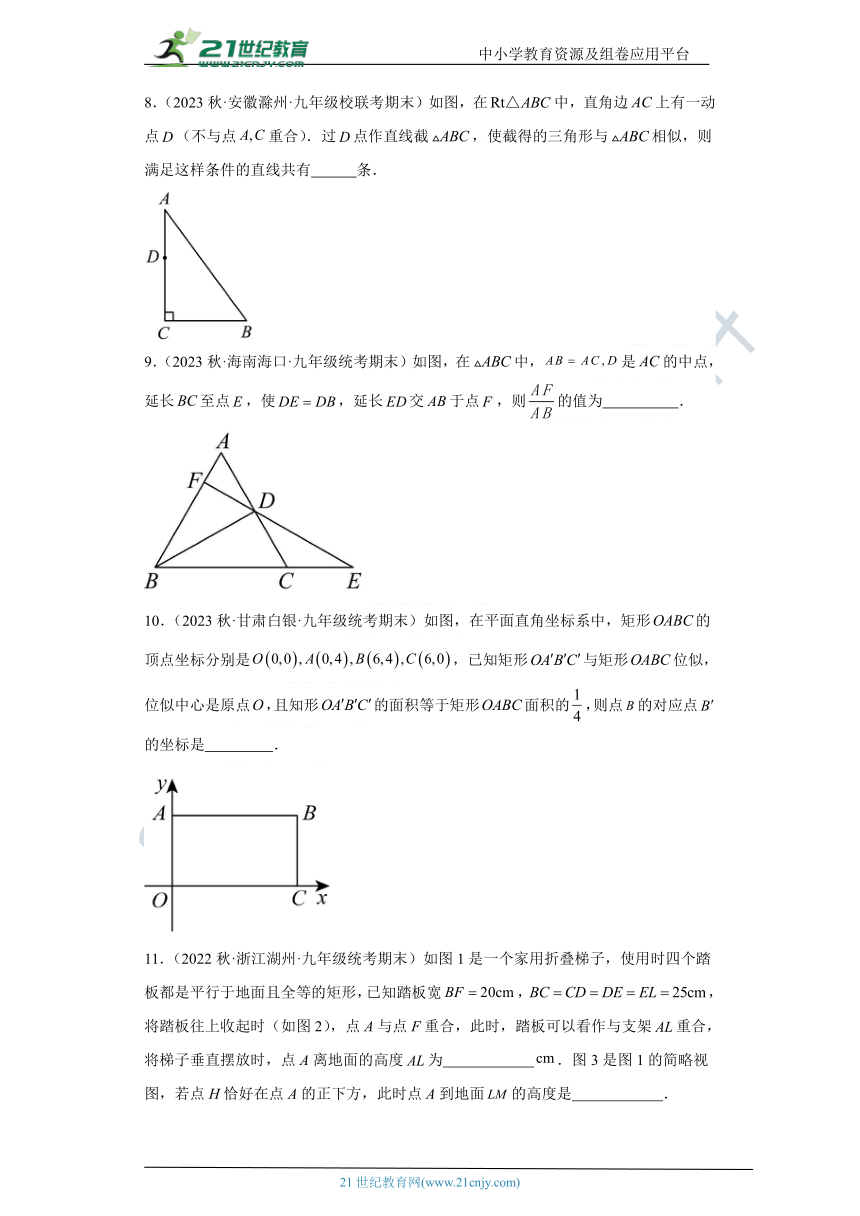
2.(2022秋·山西临汾·九年级统考期末)如图,每个小正方形边长均为1,则图中的三角形中与相似的是( )
A. B. C. D.
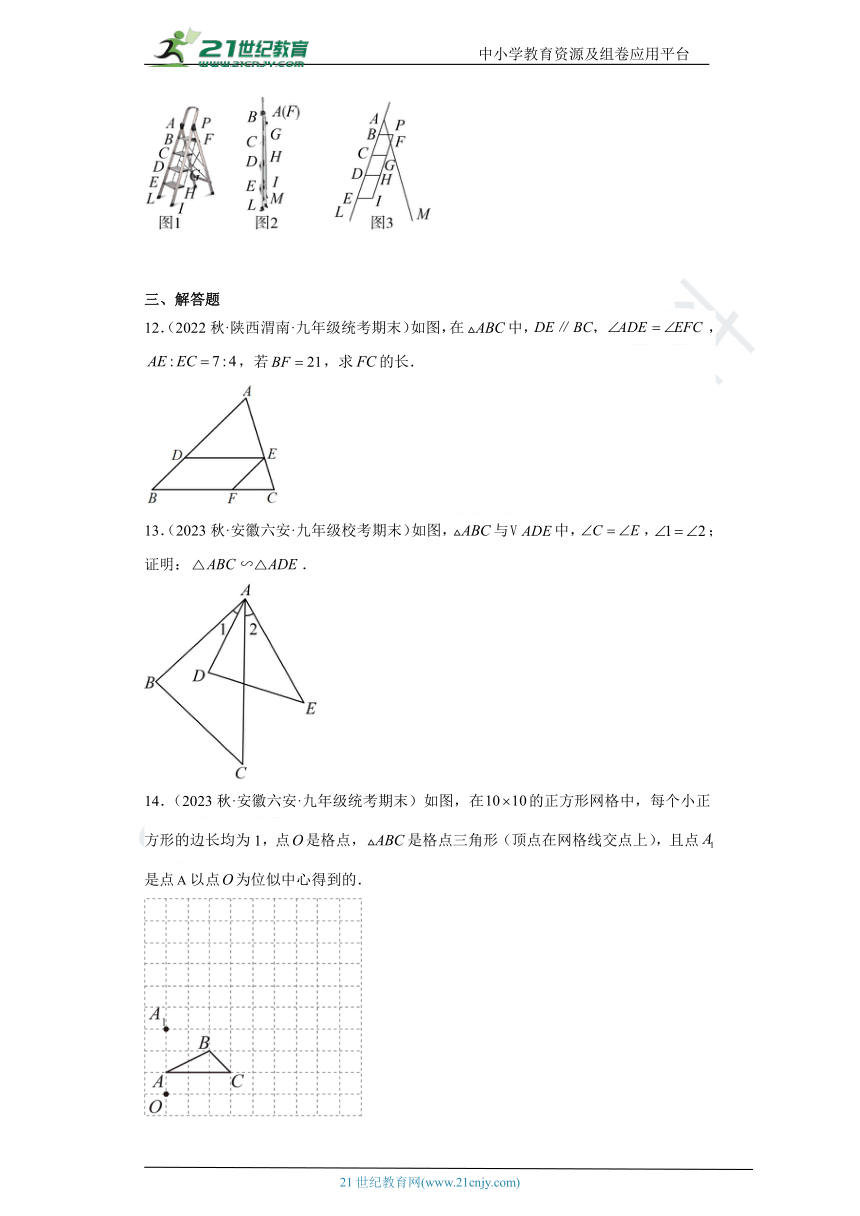
3.(2023秋·山东聊城·九年级统考期末)如图,中,,垂足为D,,垂足为E,与相交于点F,连接,给出以下四个结论:①;②;③;④.其中一定不正确的是( )
A.① B.② C.③ D.④
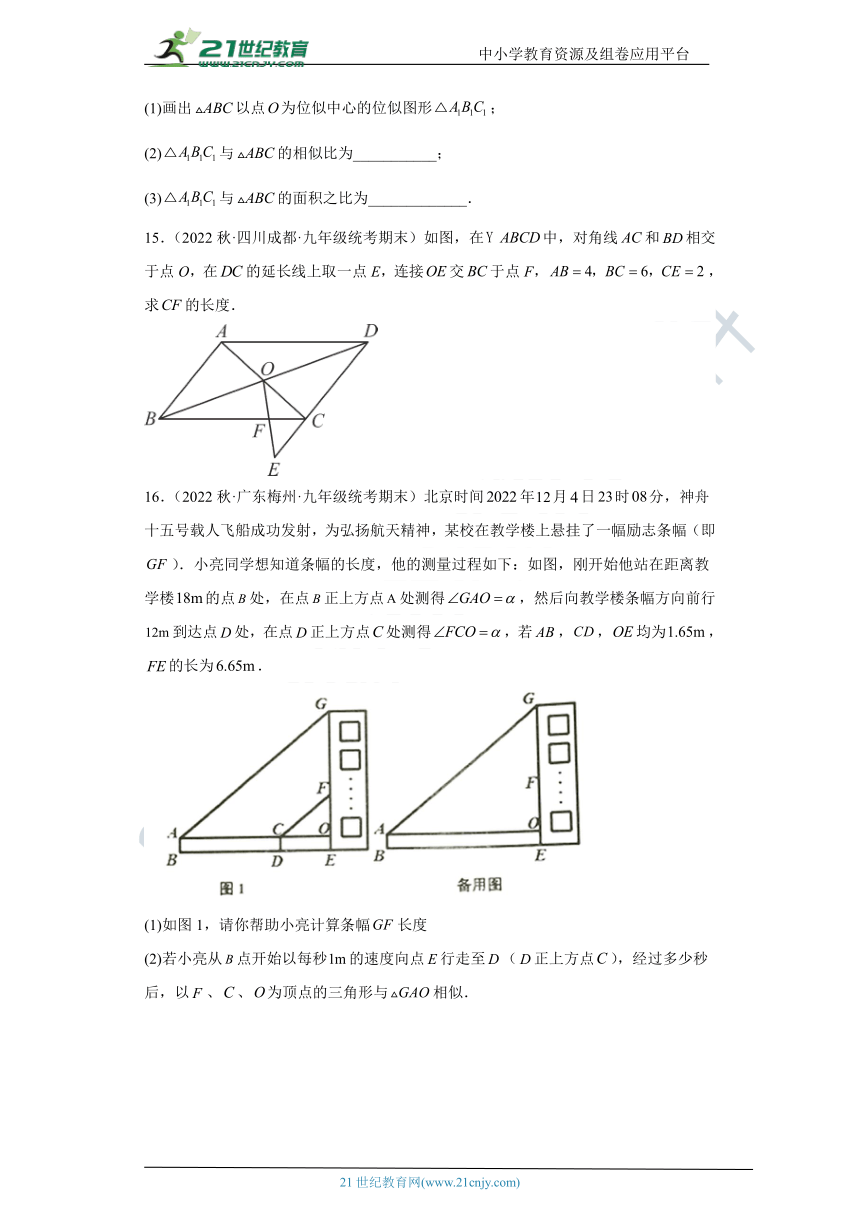
4.(2023秋·陕西咸阳·九年级统考期末)如图,以点O为位似中心,将放大得到.若,则与的周长之比为( )
A. B. C. D.
5.(2023秋·河南漯河·九年级统考期末)如图,和是以点为位似中心的位似图形,且,则下列结论中正确的是( )
A. B. C. D.
6.(2023秋·山西阳泉·九年级统考期末)如图,左、右并排的两棵大树的高分别为,,两树底部的距离,王红估计自己眼睛距地面1.6m.她沿着连接这两棵树的一条水平直路l从左向右前进,在前进的过程中,她发现看不到右边较高的树的顶端C.此时,她与左边较低的树的水平距离( )
A.小于8m B.小于9m C.大于8m D.大于9m
二、填空题
7.(2023秋·山西大同·九年级统考期末)如图,在中,是的中点,是的中点,则的长为 .
8.(2023秋·安徽滁州·九年级校联考期末)如图,在中,直角边上有一动点(不与点重合).过点作直线截,使截得的三角形与相似,则满足这样条件的直线共有 条.
9.(2023秋·海南海口·九年级统考期末)如图,在中,是的中点,延长至点,使,延长交于点,则的值为 .
10.(2023秋·甘肃白银·九年级统考期末)如图,在平面直角坐标系中,矩形的顶点坐标分别是,已知矩形与矩形位似,位似中心是原点,且知形的面积等于矩形面积的,则点的对应点的坐标是 .
11.(2022秋·浙江湖州·九年级统考期末)如图1是一个家用折叠梯子,使用时四个踏板都是平行于地面且全等的矩形,已知踏板宽,,将踏板往上收起时(如图2),点A与点F重合,此时,踏板可以看作与支架重合,将梯子垂直摆放时,点A离地面的高度为 .图3是图1的简略视图,若点H恰好在点A的正下方,此时点A到地面的高度是 .
三、解答题
12.(2022秋·陕西渭南·九年级统考期末)如图,在中,,,若,求的长.
13.(2023秋·安徽六安·九年级校考期末)如图,与中,,;证明:.
14.(2023秋·安徽六安·九年级统考期末)如图,在的正方形网格中,每个小正方形的边长均为1,点是格点,是格点三角形(顶点在网格线交点上),且点是点以点为位似中心得到的.
(1)画出以点为位似中心的位似图形;
(2)与的相似比为___________;
(3)与的面积之比为_____________.
15.(2022秋·四川成都·九年级统考期末)如图,在中,对角线和相交于点O,在的延长线上取一点E,连接交于点F,,求的长度.
16.(2022秋·广东梅州·九年级统考期末)北京时间年月日时分,神舟十五号载人飞船成功发射,为弘扬航天精神,某校在教学楼上悬挂了一幅励志条幅(即).小亮同学想知道条幅的长度,他的测量过程如下:如图,刚开始他站在距离教学楼的点处,在点正上方点处测得,然后向教学楼条幅方向前行到达点处,在点正上方点处测得,若,,均为,的长为.
(1)如图1,请你帮助小亮计算条幅长度
(2)若小亮从点开始以每秒的速度向点行走至(正上方点),经过多少秒后,以、、为顶点的三角形与相似.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】根据平行线分线段成比例定理得到,根据合比性质即得.
【详解】,
,
.
故选:A.
【点睛】本题主要考查了平行线分线段,解决问题的关键是熟练掌握平行线分线段成比例定理,合比性质.
2.B
【分析】直接利用相似三角形的判定方法结合正方形的性质分析得出答案.
【详解】解:由题意可得:,,
,,,,
,,
,
又,
.
故选:B.
【点睛】此题主要考查了相似三角形的判定,正确得出对应边的关系是解题关键.
3.C
【分析】根据两组对应角分别相等的两个三角形相似,相似多边形的对应边成比例逐项判断即可.
【详解】解:∵,
∴,即①正确;
∵,
∴,
∴,即,②正确;
∴④正确;
∵题中条件没有给出边的关系,
∴不能确定,③不一定正确.
故选:C.
【点睛】本题考查了相似三角形的判定和性质,灵活利用相似三角形的判定和性质是解题关键.
4.D
【分析】根据题意求出与的位似比,得到相似比,周长之比等于相似比.
【详解】解:以点O为位似中心,将放大得到,
∴,
∵,
∴,
∴与的位似比为,
∴与的周长之比为.
故选:D.
【点睛】本题考查的是位似变换,位似是相似的特殊形式,位似比等于相似比,其对应的周长之比等于相似比.
5.C
【分析】根据题意可得,进而根据相似三角形的性质即可求解.
【详解】解:∵和是以点为位似中心的位似图形,
∴
∴,
∴,故C正确
∵,
∴
∴,,,故A,B,D选项不正确,
故选:C.
【点睛】本题考查了位似图形的性质,相似三角形的性质,熟练掌握相似三角形的性质与判定是解题的关键.
6.A
【分析】连接并延长交于点N,过N作于点M,设,证明,由相似三角形的性质即可求得x的值,从而确定答案.
【详解】解:如图,连接并延长交于点N,过N作于点M,
∵,均垂直于直线,
∴,
∴,;
由题意知,四边形是矩形,则;
设,则,
∵,
∴,
∴,
即,
解得:;
当王红刚好看到右边较高的树的顶端C时,她与左边较低的树的水平距离为,当她看不到较高的树的顶端C时,则她与左边较低的树的水平距离应小于;
故选:A.
【点睛】本题考查了相似三角形的实际应用,正确理解题意,灵活利用相似三角形的性质是解题的关键.
7.
【分析】如图,取的中点F,连接,由中位线定理得,由平行线分线段成比例定理,得,所以,得出结论.
【详解】解:如图,取的中点F,连接,
∵,
∴是的中位线,
∴,
∴,
∵,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查中位线定理,平行线分线段成比例定理,添加辅助线,构造中位线是解题的关键.
8.3
【分析】根据平行于三角形一边的直线截另两边或另两边的延长线所得三角形与原三角形相似,可以作,;又由有两个角对应相等的三角形相似,可以过点作于点.即可获得答案.
【详解】解:这样的直线有3条:
①如图1:作,∴;
②如图2:作,∴;
③如图3:过点作于点,
∴,
∵,
∴.
故答案为:3.
【点睛】此题主要考查了三角形相似的判定方法,解题关键是理解并掌握平行于三角形一边的直线截另两边或另两边的延长线所得三角形与原三角形相似,有两个角对应相等的三角形相似.
9.
【分析】根据“等边对等角”可得,从而可得,由此可证∽,列比例式可得的值,再由,是的中点,即可得出的值.
【详解】,
.
,
.
又,
.
,
.
又,
∽,
.
,
,
,
,
,
.
故答案为:.
【点睛】本题主要考查了等腰三角形的性质和相似三角形的判定与性质.熟练掌握以上知识是解题的关键.
10.或/或
【分析】根据位似图形的概念得到矩形矩形,根据相似多边形的性质求出相似比,根据位似图形与坐标的关系计算,得到答案.
【详解】解:∵矩形与矩形关于点O位似,
∴矩形矩形,
∵矩形的面积等于矩形面积的,
∴矩形与矩形的相似比为,
∵,
∴点的坐标为或,即或,
故答案为:或.
【点睛】本题考查的是位似变换的概念和性质,掌握位似图形是相似图形以及相似多边形的性质是解题的关键.相似图形面积比等于相似比的平方.
11. 120
【分析】由点A与点F重合能够得出的长,从而可以求出点A离地面的高度.连接并延长,交于点Q,得到直角三角形,又由使用时四个踏板都是平行于地面且全等的矩形,得到,得到,利用相似三角形的性质可以求出的长,进而利用勾股定理可以求出点A到地面的高度.
【详解】∵将踏板往上收起时(如图2),点A与点F重合,
∴.
∴,
即点A离地面的高度为120 .
如图,连接并延长,交于点Q,则.
∵使用时四个踏板都是平行于地面且全等的矩形,
∴,,
∴,
∴,
即,
解得.
在中,由勾股定理,得
,
即点A到地面的高度是.
故答案为:120,.
【点睛】本题是一道实际应用题,主要考查了相似三角形的判定与性质、等腰三角形的性质、勾股定理等知识,正确理解题意,能够将实际问题转化成数学问题是解题的关键.
12.
【分析】根据平行线的性质得出,结合已知条件证明,根据平行线分线段成比例即可求解.
【详解】,
,
,
,
,
,
,
,
解得:.
【点睛】本题考查了平行线的性质与判定,平行线分线段成比例,熟练掌握平行线分线段成比例是解题的关键.
13.见解析
【分析】根据,得出,进而可得出结论.
【详解】证明:∵,
∴,
∴,
∵,
∴.
【点睛】本题考查相似三角形的判定,掌握相似三角形的判定定理是解题的关键.
14.(1)见解析
(2)
(3)
【分析】(1)直接利用A点对应点位置结合位似中心得出B,C点对应点;
(2)利用所画图形,结合对应点与位似中心的距离得出位似比;
(3)得出三角形面积即可得出答案.
【详解】(1)解:如图所示,即为所求;
(2)解:∵由图可知,,
∴与的位似比为;
(3)解:∵,,
∴与的面积比为.
【点睛】此题主要考查了位似变换以及勾股定理,正确得出对应点位置是解题关键.
15.
【分析】如图,过作,交于,则,,由平行四边形的性质可得,解得,,则,证明,则,计算求解即可.
【详解】解:如图,过作,交于,
∴,
∴,
∵,
∴,解得,,
∴,
∵,
∴,
∵,,,
∴,
∴,
∴的长为.
【点睛】本题考查了平行四边形的性质,相似三角形的判定与性质,平行线的性质,全等三角形的判定与性质.解题的关键在于对知识的熟练掌握与灵活运用.
16.(1)
(2)秒或秒
【分析】(1)根据已知求出、和,再根据同位角相等求出,根据成比例线段求出长度;
(2)设经过秒后,以、、为顶点的三角形与相似,则,,利用三角形相似对应边成比例,分成和两种情况求解即可.
【详解】(1)解:由题意得:,,,
,
,
,即,
解得,
条幅的长度为;
(2)设经过秒后,以、、为顶点的三角形与相似,则,,
当时,,即,
解得,
当时,,即,
解得,
∴经过秒或秒后,以、、为顶点的三角形与相似.
【点睛】本题考查了相似三角形的应用,平行线的判定,平行线分线段成比例,熟练掌握并灵活运用这些性质是解答本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第22章 相似形 单元练习 2023-2024学年 沪科版(2012)九年级数学上册 (含解析)
一、单选题
1.(2022秋·安徽六安·九年级校考期末)如图,,两条直线与这三条平行线分别交于点A、、和、、,若,则的值为( )
A. B. C. D.
2.(2022秋·山西临汾·九年级统考期末)如图,每个小正方形边长均为1,则图中的三角形中与相似的是( )
A. B. C. D.
3.(2023秋·山东聊城·九年级统考期末)如图,中,,垂足为D,,垂足为E,与相交于点F,连接,给出以下四个结论:①;②;③;④.其中一定不正确的是( )
A.① B.② C.③ D.④
4.(2023秋·陕西咸阳·九年级统考期末)如图,以点O为位似中心,将放大得到.若,则与的周长之比为( )
A. B. C. D.
5.(2023秋·河南漯河·九年级统考期末)如图,和是以点为位似中心的位似图形,且,则下列结论中正确的是( )
A. B. C. D.
6.(2023秋·山西阳泉·九年级统考期末)如图,左、右并排的两棵大树的高分别为,,两树底部的距离,王红估计自己眼睛距地面1.6m.她沿着连接这两棵树的一条水平直路l从左向右前进,在前进的过程中,她发现看不到右边较高的树的顶端C.此时,她与左边较低的树的水平距离( )
A.小于8m B.小于9m C.大于8m D.大于9m
二、填空题
7.(2023秋·山西大同·九年级统考期末)如图,在中,是的中点,是的中点,则的长为 .
8.(2023秋·安徽滁州·九年级校联考期末)如图,在中,直角边上有一动点(不与点重合).过点作直线截,使截得的三角形与相似,则满足这样条件的直线共有 条.
9.(2023秋·海南海口·九年级统考期末)如图,在中,是的中点,延长至点,使,延长交于点,则的值为 .
10.(2023秋·甘肃白银·九年级统考期末)如图,在平面直角坐标系中,矩形的顶点坐标分别是,已知矩形与矩形位似,位似中心是原点,且知形的面积等于矩形面积的,则点的对应点的坐标是 .
11.(2022秋·浙江湖州·九年级统考期末)如图1是一个家用折叠梯子,使用时四个踏板都是平行于地面且全等的矩形,已知踏板宽,,将踏板往上收起时(如图2),点A与点F重合,此时,踏板可以看作与支架重合,将梯子垂直摆放时,点A离地面的高度为 .图3是图1的简略视图,若点H恰好在点A的正下方,此时点A到地面的高度是 .
三、解答题
12.(2022秋·陕西渭南·九年级统考期末)如图,在中,,,若,求的长.
13.(2023秋·安徽六安·九年级校考期末)如图,与中,,;证明:.
14.(2023秋·安徽六安·九年级统考期末)如图,在的正方形网格中,每个小正方形的边长均为1,点是格点,是格点三角形(顶点在网格线交点上),且点是点以点为位似中心得到的.
(1)画出以点为位似中心的位似图形;
(2)与的相似比为___________;
(3)与的面积之比为_____________.
15.(2022秋·四川成都·九年级统考期末)如图,在中,对角线和相交于点O,在的延长线上取一点E,连接交于点F,,求的长度.
16.(2022秋·广东梅州·九年级统考期末)北京时间年月日时分,神舟十五号载人飞船成功发射,为弘扬航天精神,某校在教学楼上悬挂了一幅励志条幅(即).小亮同学想知道条幅的长度,他的测量过程如下:如图,刚开始他站在距离教学楼的点处,在点正上方点处测得,然后向教学楼条幅方向前行到达点处,在点正上方点处测得,若,,均为,的长为.
(1)如图1,请你帮助小亮计算条幅长度
(2)若小亮从点开始以每秒的速度向点行走至(正上方点),经过多少秒后,以、、为顶点的三角形与相似.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.A
【分析】根据平行线分线段成比例定理得到,根据合比性质即得.
【详解】,
,
.
故选:A.
【点睛】本题主要考查了平行线分线段,解决问题的关键是熟练掌握平行线分线段成比例定理,合比性质.
2.B
【分析】直接利用相似三角形的判定方法结合正方形的性质分析得出答案.
【详解】解:由题意可得:,,
,,,,
,,
,
又,
.
故选:B.
【点睛】此题主要考查了相似三角形的判定,正确得出对应边的关系是解题关键.
3.C
【分析】根据两组对应角分别相等的两个三角形相似,相似多边形的对应边成比例逐项判断即可.
【详解】解:∵,
∴,即①正确;
∵,
∴,
∴,即,②正确;
∴④正确;
∵题中条件没有给出边的关系,
∴不能确定,③不一定正确.
故选:C.
【点睛】本题考查了相似三角形的判定和性质,灵活利用相似三角形的判定和性质是解题关键.
4.D
【分析】根据题意求出与的位似比,得到相似比,周长之比等于相似比.
【详解】解:以点O为位似中心,将放大得到,
∴,
∵,
∴,
∴与的位似比为,
∴与的周长之比为.
故选:D.
【点睛】本题考查的是位似变换,位似是相似的特殊形式,位似比等于相似比,其对应的周长之比等于相似比.
5.C
【分析】根据题意可得,进而根据相似三角形的性质即可求解.
【详解】解:∵和是以点为位似中心的位似图形,
∴
∴,
∴,故C正确
∵,
∴
∴,,,故A,B,D选项不正确,
故选:C.
【点睛】本题考查了位似图形的性质,相似三角形的性质,熟练掌握相似三角形的性质与判定是解题的关键.
6.A
【分析】连接并延长交于点N,过N作于点M,设,证明,由相似三角形的性质即可求得x的值,从而确定答案.
【详解】解:如图,连接并延长交于点N,过N作于点M,
∵,均垂直于直线,
∴,
∴,;
由题意知,四边形是矩形,则;
设,则,
∵,
∴,
∴,
即,
解得:;
当王红刚好看到右边较高的树的顶端C时,她与左边较低的树的水平距离为,当她看不到较高的树的顶端C时,则她与左边较低的树的水平距离应小于;
故选:A.
【点睛】本题考查了相似三角形的实际应用,正确理解题意,灵活利用相似三角形的性质是解题的关键.
7.
【分析】如图,取的中点F,连接,由中位线定理得,由平行线分线段成比例定理,得,所以,得出结论.
【详解】解:如图,取的中点F,连接,
∵,
∴是的中位线,
∴,
∴,
∵,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查中位线定理,平行线分线段成比例定理,添加辅助线,构造中位线是解题的关键.
8.3
【分析】根据平行于三角形一边的直线截另两边或另两边的延长线所得三角形与原三角形相似,可以作,;又由有两个角对应相等的三角形相似,可以过点作于点.即可获得答案.
【详解】解:这样的直线有3条:
①如图1:作,∴;
②如图2:作,∴;
③如图3:过点作于点,
∴,
∵,
∴.
故答案为:3.
【点睛】此题主要考查了三角形相似的判定方法,解题关键是理解并掌握平行于三角形一边的直线截另两边或另两边的延长线所得三角形与原三角形相似,有两个角对应相等的三角形相似.
9.
【分析】根据“等边对等角”可得,从而可得,由此可证∽,列比例式可得的值,再由,是的中点,即可得出的值.
【详解】,
.
,
.
又,
.
,
.
又,
∽,
.
,
,
,
,
,
.
故答案为:.
【点睛】本题主要考查了等腰三角形的性质和相似三角形的判定与性质.熟练掌握以上知识是解题的关键.
10.或/或
【分析】根据位似图形的概念得到矩形矩形,根据相似多边形的性质求出相似比,根据位似图形与坐标的关系计算,得到答案.
【详解】解:∵矩形与矩形关于点O位似,
∴矩形矩形,
∵矩形的面积等于矩形面积的,
∴矩形与矩形的相似比为,
∵,
∴点的坐标为或,即或,
故答案为:或.
【点睛】本题考查的是位似变换的概念和性质,掌握位似图形是相似图形以及相似多边形的性质是解题的关键.相似图形面积比等于相似比的平方.
11. 120
【分析】由点A与点F重合能够得出的长,从而可以求出点A离地面的高度.连接并延长,交于点Q,得到直角三角形,又由使用时四个踏板都是平行于地面且全等的矩形,得到,得到,利用相似三角形的性质可以求出的长,进而利用勾股定理可以求出点A到地面的高度.
【详解】∵将踏板往上收起时(如图2),点A与点F重合,
∴.
∴,
即点A离地面的高度为120 .
如图,连接并延长,交于点Q,则.
∵使用时四个踏板都是平行于地面且全等的矩形,
∴,,
∴,
∴,
即,
解得.
在中,由勾股定理,得
,
即点A到地面的高度是.
故答案为:120,.
【点睛】本题是一道实际应用题,主要考查了相似三角形的判定与性质、等腰三角形的性质、勾股定理等知识,正确理解题意,能够将实际问题转化成数学问题是解题的关键.
12.
【分析】根据平行线的性质得出,结合已知条件证明,根据平行线分线段成比例即可求解.
【详解】,
,
,
,
,
,
,
,
解得:.
【点睛】本题考查了平行线的性质与判定,平行线分线段成比例,熟练掌握平行线分线段成比例是解题的关键.
13.见解析
【分析】根据,得出,进而可得出结论.
【详解】证明:∵,
∴,
∴,
∵,
∴.
【点睛】本题考查相似三角形的判定,掌握相似三角形的判定定理是解题的关键.
14.(1)见解析
(2)
(3)
【分析】(1)直接利用A点对应点位置结合位似中心得出B,C点对应点;
(2)利用所画图形,结合对应点与位似中心的距离得出位似比;
(3)得出三角形面积即可得出答案.
【详解】(1)解:如图所示,即为所求;
(2)解:∵由图可知,,
∴与的位似比为;
(3)解:∵,,
∴与的面积比为.
【点睛】此题主要考查了位似变换以及勾股定理,正确得出对应点位置是解题关键.
15.
【分析】如图,过作,交于,则,,由平行四边形的性质可得,解得,,则,证明,则,计算求解即可.
【详解】解:如图,过作,交于,
∴,
∴,
∵,
∴,解得,,
∴,
∵,
∴,
∵,,,
∴,
∴,
∴的长为.
【点睛】本题考查了平行四边形的性质,相似三角形的判定与性质,平行线的性质,全等三角形的判定与性质.解题的关键在于对知识的熟练掌握与灵活运用.
16.(1)
(2)秒或秒
【分析】(1)根据已知求出、和,再根据同位角相等求出,根据成比例线段求出长度;
(2)设经过秒后,以、、为顶点的三角形与相似,则,,利用三角形相似对应边成比例,分成和两种情况求解即可.
【详解】(1)解:由题意得:,,,
,
,
,即,
解得,
条幅的长度为;
(2)设经过秒后,以、、为顶点的三角形与相似,则,,
当时,,即,
解得,
当时,,即,
解得,
∴经过秒或秒后,以、、为顶点的三角形与相似.
【点睛】本题考查了相似三角形的应用,平行线的判定,平行线分线段成比例,熟练掌握并灵活运用这些性质是解答本题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
