华东师大版九年级数学上册 23.3.4相似三角形应用----“一线三等角”相似模型 讲义 (无答案)
文档属性
| 名称 | 华东师大版九年级数学上册 23.3.4相似三角形应用----“一线三等角”相似模型 讲义 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 419.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 21:37:44 | ||
图片预览


文档简介
“一线三等角”模型
【知识梳理】
一线三等角
1. 如图1,∠ACB=∠D=∠E=90°且∠CAB=45°→△ACD≌△CBE,此为:“一线三直角”全等,又
称“K字型”全等;
(
A
B
D
E
C
45
°
) (
A
B
C
E
D
α
) (
A
B
C
D
E
)
图1 图2 图3
2. 如图2,∠ACB=∠D=∠E=90°→△ACD∽△CBE,此为:“一线三直角”相似,又称:“K字型”相似;
3. 如图3,∠ACB=∠D=∠E→△ACD∽△CBE,此为更一般的“一线三等角”.
怎么用?
1.找模型
在两个三角形中有一条边共线,且有三个角相等时,考虑“一线三等角”相似模型
2.用模型
确定一线三等角后,依据平角性质,三角形的内角和及内外角关系导角证得相似,再利用相似性质解题
“一线三等角”的应用分三重境界:
一重境:当一条线上已有三个等角时,只要识别、证明,直接应用模型解题,如图1所示的“同侧型一线三等角”及图2所示的“异侧型一线三等角”;
二重境:当一条线上已有两个等角时,需要再补上一个等角,构造模型解题;
三重镜:当一条线上只有一个角时,需要再补上两个等角,构造模型解题,如图3及图4所示;
图1 图2 图3 图4
【考点剖析】
例1.例1如图,在边长为7的等边△ABC中,点D是BC上的动点,∠MDN =60°,若BD=2,NC=4,则BM的长为( )
A. B.2 c. D.3
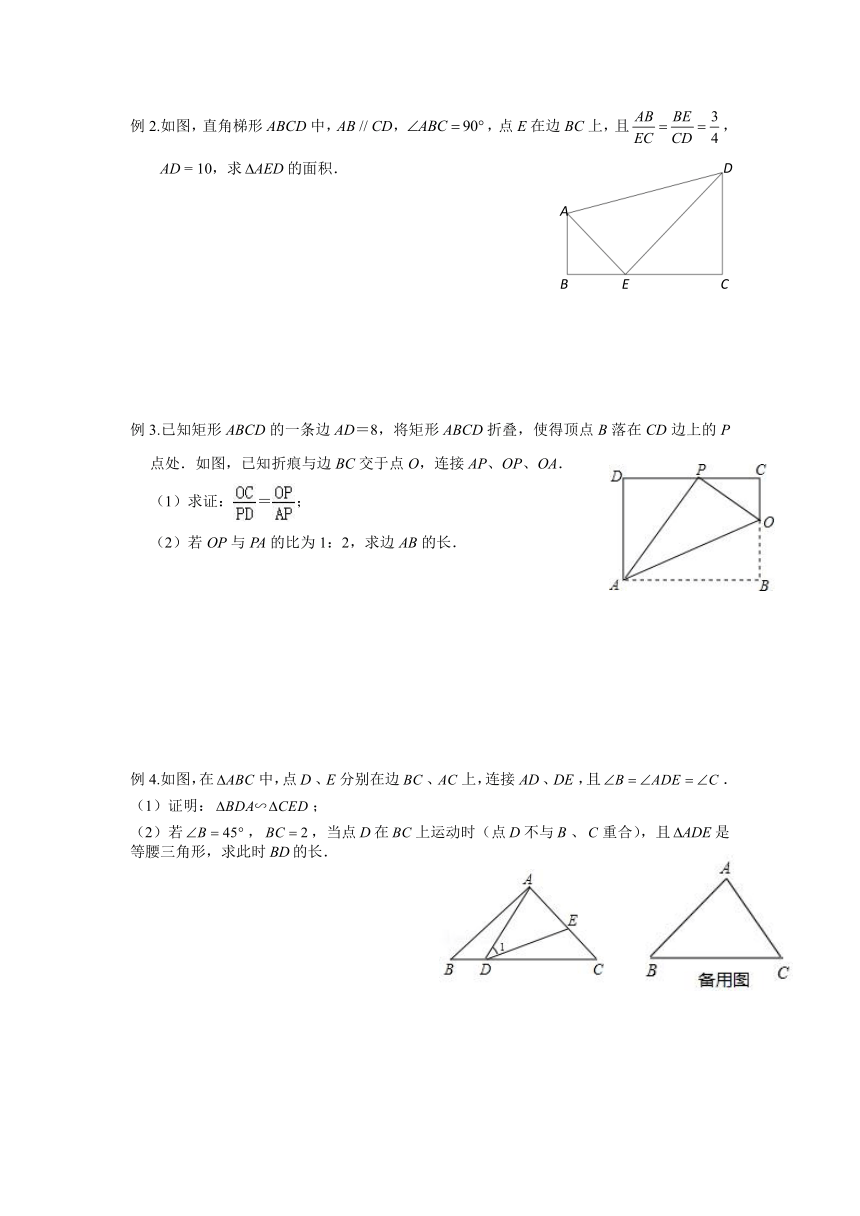
例2.如图,直角梯形ABCD中,AB // CD,,点E在边BC上,且, AD = 10,求的面积.
例3.已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连接AP、OP、OA.
(1)求证:=;
(2)若OP与PA的比为1:2,求边AB的长.
例4.如图,在中,点、分别在边、上,连接、,且.
(1)证明:;
(2)若,,当点在上运动时(点不与、重合),且是等腰三角形,求此时的长.
例5.如图,直线y与双曲线y(x>0)的交点为A,与x轴的交点为B.
(1)求∠ABO的度数;
(2)求AB的长;
(3)已知点C为双曲线y(x>0)上的一点,当∠AOC=60°时,求点C的坐标.
例6.如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段AM最短时,求重叠部分的面积.
【过关检测】
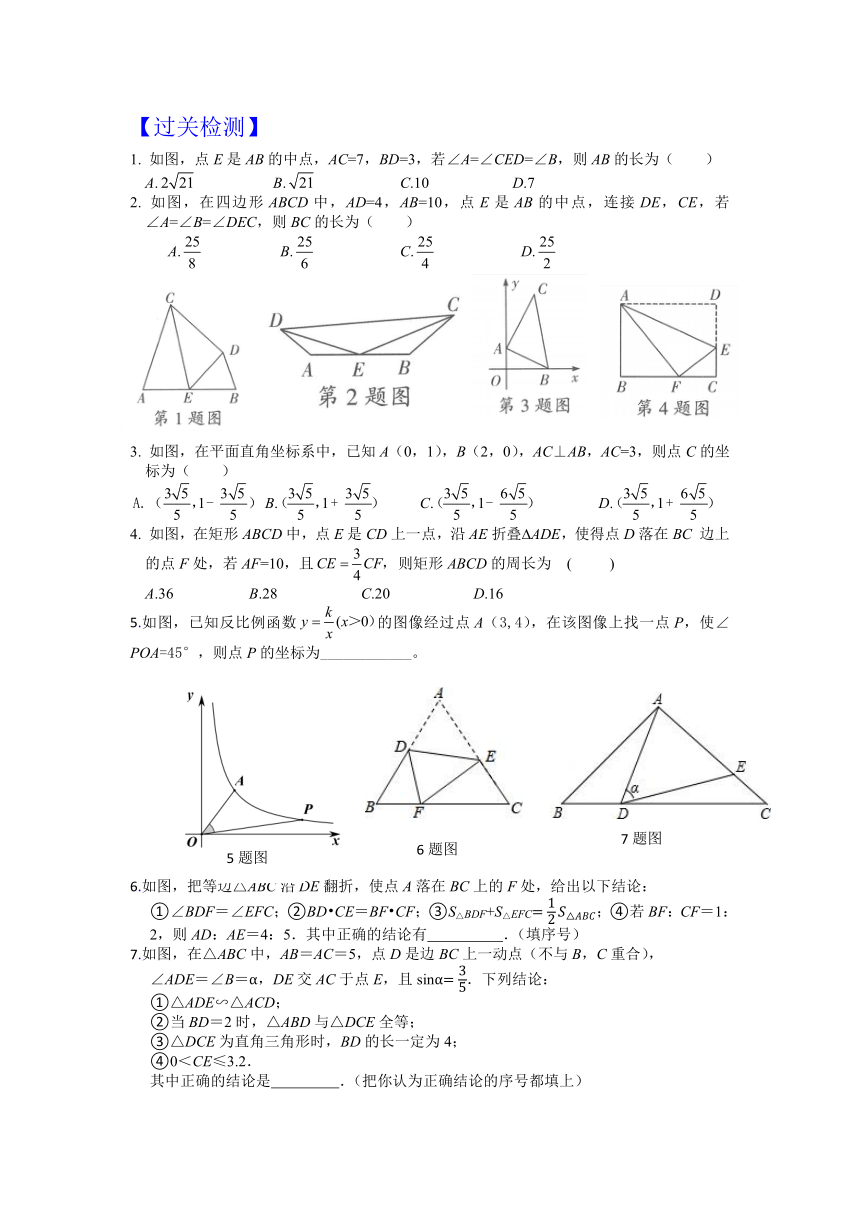
1. 如图,点E是AB的中点,AC=7,BD=3,若∠A=∠CED=∠B,则AB的长为( )
A. B. C.10 D.7
2. 如图,在四边形ABCD中,AD=4,AB=10,点E是AB的中点,连接DE,CE,若∠A=∠B=∠DEC,则BC的长为( )
A. B. C. D.
3. 如图,在平面直角坐标系中,已知A(0,1),B(2,0),AC⊥AB,AC=3,则点C的坐标为( )
B. C. D.
4. 如图,在矩形ABCD中,点E是CD上一点,沿AE折叠 ADE,使得点D落在BC 边上的点F处,若AF=10,且 则矩形ABCD的周长为 ( )
A.36 B.28 C.20 D.16
5.如图,已知反比例函数的图像经过点A(3,4),在该图像上找一点P,使∠POA=45°,则点P的坐标为____________。
6.如图,把等边△ABC沿DE翻折,使点A落在BC上的F处,给出以下结论:
①∠BDF=∠EFC;②BD CE=BF CF;③S△BDF+S△EFC;④若BF:CF=1:2,则AD:AE=4:5.其中正确的结论有 .(填序号)
7.如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),
∠ADE=∠B=α,DE交AC于点E,且sinα.下列结论:
①△ADE∽△ACD;
②当BD=2时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD的长一定为4;
④0<CE≤3.2.
其中正确的结论是 .(把你认为正确结论的序号都填上)
8.已知:如图,△ABC与△ADE均为等腰三角形,BA=BC,DA=DE,如果点D在BC上,且∠EDC=∠BAD,点O为AC与DE的交点.
求证:(1)△ABC∽△ADE;
(2)DA OE=OA CE.
9.如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于F,交AD的延长线于点E.
(1)求证:△ABM∽△MCF;
(2)若AB=4,BM=2,求△DEF的面积.
10.如图,∠C=∠CBD=90°,DE⊥AB于点E.
(1)求证:△DBE∽△BAC.
(2)若BC=3,DB=2,CA=1,求DE的长.
11.矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)如图2,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M、N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.
12.已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:
(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
13.如图1,在四边形ABCD中,AC是对角线,且AB=AC.F是BC边上一动点,连接AF,DF,DF交AC于点E,其中∠DAF=90°,∠AFD=∠B.
(1)求证:AC EC=BF CF;
(2)若AB=AC=10,BC=16.
①如图2,若DF∥AB,求的值;
②如图3,若DF=DC,求△DCF的面积.
14.在平面直角坐标系xOy中,点B(0,3),点C(4,0)
(1)求线段BC的长.
(2)如图1,点A(﹣1,0),D是线段BC上的一点,若△BAD∽△BCA时,求点D的坐标.
(3)如图2,以BC为边在第一象限内作等边△BCE,求点E的坐标.
15.如图,在△ABC中,已知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.
(1)求证:△ABP∽△PCM;
(2)在P点运动过程中,若PM∥AB,请求出线段BP的长;
(3)探究:在P点运动过程中,连接BM,设△ABM的面积为S,试分析S是否存在最小值,如果存在,求出这个最小值;如果不存在,说明理由.
【知识梳理】
一线三等角
1. 如图1,∠ACB=∠D=∠E=90°且∠CAB=45°→△ACD≌△CBE,此为:“一线三直角”全等,又
称“K字型”全等;
(
A
B
D
E
C
45
°
) (
A
B
C
E
D
α
) (
A
B
C
D
E
)
图1 图2 图3
2. 如图2,∠ACB=∠D=∠E=90°→△ACD∽△CBE,此为:“一线三直角”相似,又称:“K字型”相似;
3. 如图3,∠ACB=∠D=∠E→△ACD∽△CBE,此为更一般的“一线三等角”.
怎么用?
1.找模型
在两个三角形中有一条边共线,且有三个角相等时,考虑“一线三等角”相似模型
2.用模型
确定一线三等角后,依据平角性质,三角形的内角和及内外角关系导角证得相似,再利用相似性质解题
“一线三等角”的应用分三重境界:
一重境:当一条线上已有三个等角时,只要识别、证明,直接应用模型解题,如图1所示的“同侧型一线三等角”及图2所示的“异侧型一线三等角”;
二重境:当一条线上已有两个等角时,需要再补上一个等角,构造模型解题;
三重镜:当一条线上只有一个角时,需要再补上两个等角,构造模型解题,如图3及图4所示;
图1 图2 图3 图4
【考点剖析】
例1.例1如图,在边长为7的等边△ABC中,点D是BC上的动点,∠MDN =60°,若BD=2,NC=4,则BM的长为( )
A. B.2 c. D.3
例2.如图,直角梯形ABCD中,AB // CD,,点E在边BC上,且, AD = 10,求的面积.
例3.已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连接AP、OP、OA.
(1)求证:=;
(2)若OP与PA的比为1:2,求边AB的长.
例4.如图,在中,点、分别在边、上,连接、,且.
(1)证明:;
(2)若,,当点在上运动时(点不与、重合),且是等腰三角形,求此时的长.
例5.如图,直线y与双曲线y(x>0)的交点为A,与x轴的交点为B.
(1)求∠ABO的度数;
(2)求AB的长;
(3)已知点C为双曲线y(x>0)上的一点,当∠AOC=60°时,求点C的坐标.
例6.如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段AM最短时,求重叠部分的面积.
【过关检测】
1. 如图,点E是AB的中点,AC=7,BD=3,若∠A=∠CED=∠B,则AB的长为( )
A. B. C.10 D.7
2. 如图,在四边形ABCD中,AD=4,AB=10,点E是AB的中点,连接DE,CE,若∠A=∠B=∠DEC,则BC的长为( )
A. B. C. D.
3. 如图,在平面直角坐标系中,已知A(0,1),B(2,0),AC⊥AB,AC=3,则点C的坐标为( )
B. C. D.
4. 如图,在矩形ABCD中,点E是CD上一点,沿AE折叠 ADE,使得点D落在BC 边上的点F处,若AF=10,且 则矩形ABCD的周长为 ( )
A.36 B.28 C.20 D.16
5.如图,已知反比例函数的图像经过点A(3,4),在该图像上找一点P,使∠POA=45°,则点P的坐标为____________。
6.如图,把等边△ABC沿DE翻折,使点A落在BC上的F处,给出以下结论:
①∠BDF=∠EFC;②BD CE=BF CF;③S△BDF+S△EFC;④若BF:CF=1:2,则AD:AE=4:5.其中正确的结论有 .(填序号)
7.如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),
∠ADE=∠B=α,DE交AC于点E,且sinα.下列结论:
①△ADE∽△ACD;
②当BD=2时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD的长一定为4;
④0<CE≤3.2.
其中正确的结论是 .(把你认为正确结论的序号都填上)
8.已知:如图,△ABC与△ADE均为等腰三角形,BA=BC,DA=DE,如果点D在BC上,且∠EDC=∠BAD,点O为AC与DE的交点.
求证:(1)△ABC∽△ADE;
(2)DA OE=OA CE.
9.如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于F,交AD的延长线于点E.
(1)求证:△ABM∽△MCF;
(2)若AB=4,BM=2,求△DEF的面积.
10.如图,∠C=∠CBD=90°,DE⊥AB于点E.
(1)求证:△DBE∽△BAC.
(2)若BC=3,DB=2,CA=1,求DE的长.
11.矩形ABCD一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)如图2,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M、N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.
12.已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:
(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
13.如图1,在四边形ABCD中,AC是对角线,且AB=AC.F是BC边上一动点,连接AF,DF,DF交AC于点E,其中∠DAF=90°,∠AFD=∠B.
(1)求证:AC EC=BF CF;
(2)若AB=AC=10,BC=16.
①如图2,若DF∥AB,求的值;
②如图3,若DF=DC,求△DCF的面积.
14.在平面直角坐标系xOy中,点B(0,3),点C(4,0)
(1)求线段BC的长.
(2)如图1,点A(﹣1,0),D是线段BC上的一点,若△BAD∽△BCA时,求点D的坐标.
(3)如图2,以BC为边在第一象限内作等边△BCE,求点E的坐标.
15.如图,在△ABC中,已知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.
(1)求证:△ABP∽△PCM;
(2)在P点运动过程中,若PM∥AB,请求出线段BP的长;
(3)探究:在P点运动过程中,连接BM,设△ABM的面积为S,试分析S是否存在最小值,如果存在,求出这个最小值;如果不存在,说明理由.
