青岛版数学七年级上册7.1等式的基本性质课件(共19张PPT)
文档属性
| 名称 | 青岛版数学七年级上册7.1等式的基本性质课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 21:37:20 | ||
图片预览






文档简介
(共19张PPT)
青岛版 数学 七年级(上) 第7章 一元一次方程
7.1 等式的基本性质
知识回顾
1、什么叫做等式?
用“=”连接,表示两个相等关系的式子叫做等式。
例如: 3+2=5; 4+7=1+10; a+b=b+a .
问题:如果在“=”的左右两边怎样运算,还能保证左右两边仍然相等呢?
“=”左边的代数式叫做等式的左边;
2、什么叫做等式的左边和右边?
“=”右边的代数式叫做等式的右边.
交流与发现(一)
思考下列问题,并与同学交流。
(1)小莹今年a岁,小亮今年b岁,再过c年他们分别是多少岁?
(2)如果小莹和小亮同岁,(即a=b),那么再过c年他们的岁数还相同吗?c年前呢?
(3)从(2)中你发现了什么结论?能用等式把它表示出来吗?
小莹(a+c)岁;小亮(b+c)岁
如果a=b,那么a+c=b+c , a-c=b-c。
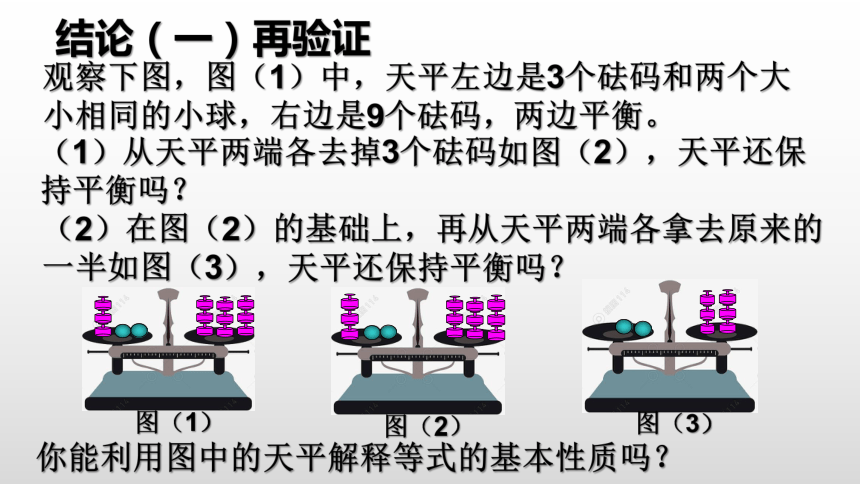
观察下图,图(1)中,天平左边是3个砝码和两个大小相同的小球,右边是9个砝码,两边平衡。
结论(一)再验证
(1)从天平两端各去掉3个砝码如图(2),天平还保持平衡吗?
(2)在图(2)的基础上,再从天平两端各拿去原来的一半如图(3),天平还保持平衡吗?
你能利用图中的天平解释等式的基本性质吗?
图(1)
图(2)
图(3)
等式的基本性质1:
等式两边都加上(或减去)同一个整式,所得的结果仍是等式。
新知识小结1
如果a=b,那么a+c=b+c , a-c=b-c。
交流与发现(二)
思考下列问题,并与同学交流。
(4)一袋巧克力糖的售价是a元,一盒果冻的售价是b元,买c袋巧克力糖和买c盒果冻各要花多少钱?
(5)如果一袋巧克力糖与一袋果冻的售价相同(即a=b),那么买c袋巧克力糖和买c盒果冻的价钱相同吗?
巧克力糖ac元,果冻bc元.
(6)从(5)中你发现了什么结论?能用等式把它表示出来吗?
如果a=b, 那么ac=bc.
交流与发现(三)
思考下列问题,并与同学交流。
(7)A,B两地相距a千米,C,D两地相距b千米,小亮第一天从A地去B地用了c小时,第二天从C地去D地也用了c小时,分别求小亮这两天的平均速度?
(8)如果A,B两地距离和C,D两地距离相同(即a=b),那么小亮这两天的平均速度相同吗?
(9)从(8)中你发现了什么结论?能用等式把它表示出来吗?
如果a=b,那么
等式的基本性质2:
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式。
新知识小结2
① 如果a=b, 那么ac=bc.
② 如果a=b,那么
注意:除数不能为0.
(1)如果x=y,那么x+1=y+3. ( )
(2)如果x=y,那么x+5-a=y+5-a. ( )
(3)如果x=y,那么2x=3y. ( )
(4)如果x=y,那么 . ( )
(5)如果x=y,那么 . ( )
(6)如果x=y,且a≠1,那么 .( )
例1、判断对错,对的请说出根据等式的哪一条性
质,错的请说出为什么。
√
×
×
×
√
√
例题讲解
例题讲解
例2、在下列各题的横线上填上适当的整式,使等式成立,并说明根据的是等式的哪一条基本性质以及是怎样变形的。
(1)如果2x-5=3,那么2x=3+ _______;
(2)如果-x=1,那么x=___________.
根据等式的基本性质1,在等式两边都加上5.
根据等式的基本性质2,两边都除以(或乘)-1.
5
-1
例题讲解
(1)怎样从等式 3x=2x+7得到等式x=7
解:因为 3x=2x+7
根据等式的基本性质1,在等式两边都减去2x,得
3x-2x=2x+7-2x
所以x=7
例3、利用不等式的基本性质解释下列等式的变形:
(2)怎样从等式a2=b2得到等式a2c=b2c?
解:因为a2=b2
根据等式的基本性质2,在等式两边都乘以c,得
a2·c=b2·c
所以 a2c=b2 c
解:两边减7,得
∴
解:两边除以-5,得
例4、利用等式的性质解下列方程
例题讲解
(1)x+7=26
(2)-5x=20
∴
解:两边加5,得
化简,得
两边同乘-3,得
(1)从ax=ay能不能得到x=y 为什么?
(2)由xy=1能不能得到x= 为什么?
能力拔高
解:不能.因为a不知道是否为0.
解:能.因为隐含条件为y≠0.
课堂练习
P153 练习 第1、2题
课堂总结
等式的基本性质1:
等式两边都加上(或减去)同一个整式,所得的结果仍是等式。
如果a=b,那么a+c=b+c , a-c=b-c。
等式的基本性质2:
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式。
① 如果a=b, 那么ac=bc.
② 如果a=b,那么
注意:除数不能为0.
课下作业
P154 习题7.1 第1~5题
同学们,下课!
青岛版 数学 七年级(上) 第7章 一元一次方程
7.1 等式的基本性质
知识回顾
1、什么叫做等式?
用“=”连接,表示两个相等关系的式子叫做等式。
例如: 3+2=5; 4+7=1+10; a+b=b+a .
问题:如果在“=”的左右两边怎样运算,还能保证左右两边仍然相等呢?
“=”左边的代数式叫做等式的左边;
2、什么叫做等式的左边和右边?
“=”右边的代数式叫做等式的右边.
交流与发现(一)
思考下列问题,并与同学交流。
(1)小莹今年a岁,小亮今年b岁,再过c年他们分别是多少岁?
(2)如果小莹和小亮同岁,(即a=b),那么再过c年他们的岁数还相同吗?c年前呢?
(3)从(2)中你发现了什么结论?能用等式把它表示出来吗?
小莹(a+c)岁;小亮(b+c)岁
如果a=b,那么a+c=b+c , a-c=b-c。
观察下图,图(1)中,天平左边是3个砝码和两个大小相同的小球,右边是9个砝码,两边平衡。
结论(一)再验证
(1)从天平两端各去掉3个砝码如图(2),天平还保持平衡吗?
(2)在图(2)的基础上,再从天平两端各拿去原来的一半如图(3),天平还保持平衡吗?
你能利用图中的天平解释等式的基本性质吗?
图(1)
图(2)
图(3)
等式的基本性质1:
等式两边都加上(或减去)同一个整式,所得的结果仍是等式。
新知识小结1
如果a=b,那么a+c=b+c , a-c=b-c。
交流与发现(二)
思考下列问题,并与同学交流。
(4)一袋巧克力糖的售价是a元,一盒果冻的售价是b元,买c袋巧克力糖和买c盒果冻各要花多少钱?
(5)如果一袋巧克力糖与一袋果冻的售价相同(即a=b),那么买c袋巧克力糖和买c盒果冻的价钱相同吗?
巧克力糖ac元,果冻bc元.
(6)从(5)中你发现了什么结论?能用等式把它表示出来吗?
如果a=b, 那么ac=bc.
交流与发现(三)
思考下列问题,并与同学交流。
(7)A,B两地相距a千米,C,D两地相距b千米,小亮第一天从A地去B地用了c小时,第二天从C地去D地也用了c小时,分别求小亮这两天的平均速度?
(8)如果A,B两地距离和C,D两地距离相同(即a=b),那么小亮这两天的平均速度相同吗?
(9)从(8)中你发现了什么结论?能用等式把它表示出来吗?
如果a=b,那么
等式的基本性质2:
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式。
新知识小结2
① 如果a=b, 那么ac=bc.
② 如果a=b,那么
注意:除数不能为0.
(1)如果x=y,那么x+1=y+3. ( )
(2)如果x=y,那么x+5-a=y+5-a. ( )
(3)如果x=y,那么2x=3y. ( )
(4)如果x=y,那么 . ( )
(5)如果x=y,那么 . ( )
(6)如果x=y,且a≠1,那么 .( )
例1、判断对错,对的请说出根据等式的哪一条性
质,错的请说出为什么。
√
×
×
×
√
√
例题讲解
例题讲解
例2、在下列各题的横线上填上适当的整式,使等式成立,并说明根据的是等式的哪一条基本性质以及是怎样变形的。
(1)如果2x-5=3,那么2x=3+ _______;
(2)如果-x=1,那么x=___________.
根据等式的基本性质1,在等式两边都加上5.
根据等式的基本性质2,两边都除以(或乘)-1.
5
-1
例题讲解
(1)怎样从等式 3x=2x+7得到等式x=7
解:因为 3x=2x+7
根据等式的基本性质1,在等式两边都减去2x,得
3x-2x=2x+7-2x
所以x=7
例3、利用不等式的基本性质解释下列等式的变形:
(2)怎样从等式a2=b2得到等式a2c=b2c?
解:因为a2=b2
根据等式的基本性质2,在等式两边都乘以c,得
a2·c=b2·c
所以 a2c=b2 c
解:两边减7,得
∴
解:两边除以-5,得
例4、利用等式的性质解下列方程
例题讲解
(1)x+7=26
(2)-5x=20
∴
解:两边加5,得
化简,得
两边同乘-3,得
(1)从ax=ay能不能得到x=y 为什么?
(2)由xy=1能不能得到x= 为什么?
能力拔高
解:不能.因为a不知道是否为0.
解:能.因为隐含条件为y≠0.
课堂练习
P153 练习 第1、2题
课堂总结
等式的基本性质1:
等式两边都加上(或减去)同一个整式,所得的结果仍是等式。
如果a=b,那么a+c=b+c , a-c=b-c。
等式的基本性质2:
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式。
① 如果a=b, 那么ac=bc.
② 如果a=b,那么
注意:除数不能为0.
课下作业
P154 习题7.1 第1~5题
同学们,下课!
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
