人教版高中数学选择性必修第三册7.4二项分布与超几何分布 同步训练(含答案)
文档属性
| 名称 | 人教版高中数学选择性必修第三册7.4二项分布与超几何分布 同步训练(含答案) | 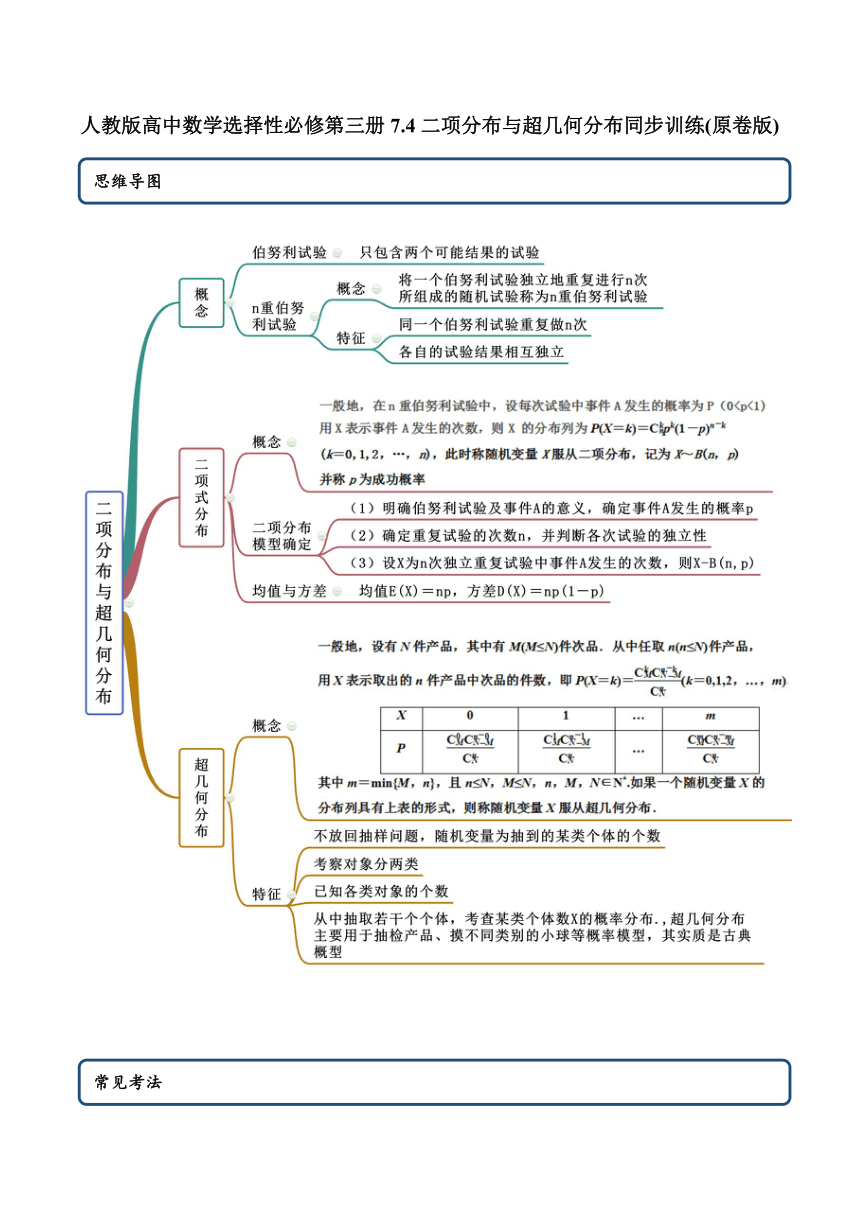 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 19:56:06 | ||
图片预览





文档简介
本资料分享自高中数学同步资源大全QQ群483122854 专注收集同步资源期待你的加入与分享
人教版高中数学选择性必修第三册7.4二项分布与超几何分布同步训练(原卷版)
考法一 二项分布
【例1】(2020·全国高二课时练习)高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行 水平间隔相等的圆柱形铁钉(如图),并且每一排铁钉数目都比上一排多一个,一排中各个铁钉恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗铁钉间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.
(1)理论上,小球落入4号容器的概率是多少?
(2)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球的个数为,求的分布列.
【一隅三反】
1.(2020·重庆市第七中学校高二月考)若随机变量,则( )
A.2 B.3 C.4 D.5
2.(多选)(2020·全国高二单元测试)已知随机变量,若使的值最大,则k等于( )
A.5 B.6 C.7 D.8
3.(2020·江苏淮安市·淮阴中学高二期末)江苏实行的“新高考方案:”模式,其中统考科目:“”指语文、数学、外语三门,不分文理:学生根据高校的要求,结合自身特长兴趣,“”指首先在在物理、历史门科目中选择一门;“”指再从思想政治、地理、化学、生物门科目中选择门某校,根据统计选物理的学生占整个学生的;并且在选物理的条件下,选择地理的概率为;在选历史的条件下,选地理的概率为.
(1)求该校最终选地理的学生概率;
(2)该校甲、乙、丙三人选地理的人数设为随机变量.
①求随机变量的概率;
②求的概率分布列以及数学期望.
4.(2020·陕西渭南市)已知某植物种子每粒成功发芽的概率都为,某植物研究所分三个小组分别独立进行该种子的发芽试验,每次试验种一粒种子,每次试验结果相互独立.假设某次试验种子发芽,则称该次试验是成功的,如果种子没有发芽,则称该次试验是失败的.
(1)第一小组做了四次试验,求该小组恰有两次失败的概率;
(2)第二小组做了四次试验,设试验成功与失败的次数的差的绝对值为,求的分布列及数学期望.
考点二 超几何分布
【例2】(2020·全国高二单元测试)现对某高校16名篮球运动员在多次训练比赛中的得分进行统计,将每位运动员的平均成绩所得数据用频率分布直方图表示如下.(如:落在区间[10,15)内的频率/组距为0.0125)规定分数在[10,20),[20,30),[30,40)上的运动员分别为三级篮球运动员、二级篮球运动员、一级篮球运动员,现从这批篮球运动员中利用分层抽样的方法选出16名运动员作为该高校的篮球运动员代表.
(1)求a的值和选出篮球运动员代表中一级运动员的人数;
(2)若从篮球运动员代表中选出三人,求其中含有一级运动员人数X的分布列;
(3)若从该校篮球运动员中有放回地选三人,求其中含有一级运动员人数Y的期望.
【一隅三反】
1.(2020·全国高二课时练习)新冠肺炎疫情期间,为了更有效地进行防控,各地学校都发出延期开学的通知.很多学校及老师为响应各地教育行政部门实行“停课不停学”的号召,让学生们在家通过收看网络直播的方式进行学习,已知高一某班共有学生21人,其中男生12人,女生9人.现采用分层抽样的方法从中抽取7人,测试他们对网络课程学习的效果,效果分为优秀和不优秀两种,优秀得2分,不优秀得1分.
(1)应抽取男生 女生各多少人?
(2)若抽取的7人中,4人的测试效果为优秀,3人为不优秀,现从这7人中随机抽取3人.
(i)用表示抽取的3人的得分之和,求随机变量x的分布列及数学期望;
(ii)设事件为“抽取的3人中,既有测试效果为优秀的,也有为不优秀的”,求事件发生的概率.
2.(2020·绵阳市·四川省绵阳江油中学)某校五四青年艺术节选拔主持人,现有来自高一年级参赛选手4名,其中男生2名;高二年级参赛选手4名,其中男生3名.从这8名参赛选手中随机选择4人组成搭档参赛.
(Ⅰ)设A为事件“选出的4人中恰有2名男生,且这2名男生来自同一个年级”,求事件A发生的概率;
(Ⅱ)设X为选出的4人中男生的人数,求随机变量X的分布列和数学期望.
3.(2021·北京东城区)为了解学生自主学习期间完成数学套卷的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
(1)从这班学生中任选一名男生,一名女生,求这两名学生完成套卷数之和为4的概率?
(2)若从完成套卷数不少于4套的学生中任选4人,设选到的男学生人数为,求随机变量的分布列和数学期望;
(3)试判断男学生完成套卷数的方差与女学生完成套卷数的方差的大小(只需写出结论).
考点三 二项分布与超几何分布综合运用
【例3】(2020·浙江台州市·高二期中)2020年五一期间,银泰百货举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有10个形状 大小完全相同的小球(其中红球2个,白球1个,黑球7个)的抽奖盒中,一次性摸出3个球其中奖规则为:若摸到2个红球和1个白球,享受免单优惠;若摸出2个红球和1个黑球则打5折;若摸出1个白球2个黑球,则打7折;其余情况不打折.方案二:从装有10个形状 大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率角度比较该顾客选择哪一种抽奖方案更合算?
【一隅三反】
1.(2020·辽宁大连市)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;
(2)求在4次游戏中获奖次数的分布列及数学期望.
2.(2020·广东云浮市)甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题,按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大
3.(2021·哈尔滨市)一批产品共10件,其中3件是不合格品,用下列两种不同方式从中随机抽取2件产品检验:
方法一:一次性随机抽取2件;
方法二:先随机抽取1件,放回后再随机抽取1件.
记方法一抽取的不合格产品数为.记方法二抽取的不合格产品数为.
(1)求两种抽取方式下,的概率分布列;
(2)比较两种抽取方式抽到的不合格品平均数的大小?并说明理由.
人教版高中数学选择性必修第三册7.4二项分布与超几何分布同步训练(解析版)
考法一 二项分布
【例1】(2020·全国高二课时练习)高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行 水平间隔相等的圆柱形铁钉(如图),并且每一排铁钉数目都比上一排多一个,一排中各个铁钉恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗铁钉间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.
(1)理论上,小球落入4号容器的概率是多少?
(2)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球的个数为,求的分布列.
【答案】(1);(2)分布列答案见解析.
【解析】(1)记“小球落入4号容器”为事件,
若要小球落入4号容器,则需要在通过的四层中有三层向右,一层向左,
∴理论上,小球落入4号容器的概率.
(2)落入4号容器的小球的个数的所有可能取值为0,1,2,3,
,
,
,
,
的分布列为
0 1 2 3
【一隅三反】
1.(2020·重庆市第七中学校高二月考)若随机变量,则( )
A.2 B.3 C.4 D.5
【答案】D
【解析】因为,所以,所以.故选:D.
2.(多选)(2020·全国高二单元测试)已知随机变量,若使的值最大,则k等于( )
A.5 B.6 C.7 D.8
【答案】BC
【解析】令,得,
即当时,;
当时,;
当时,,
所以和的值最大.
故选:BC.
3.(2020·江苏淮安市·淮阴中学高二期末)江苏实行的“新高考方案:”模式,其中统考科目:“”指语文、数学、外语三门,不分文理:学生根据高校的要求,结合自身特长兴趣,“”指首先在在物理、历史门科目中选择一门;“”指再从思想政治、地理、化学、生物门科目中选择门某校,根据统计选物理的学生占整个学生的;并且在选物理的条件下,选择地理的概率为;在选历史的条件下,选地理的概率为.
(1)求该校最终选地理的学生概率;
(2)该校甲、乙、丙三人选地理的人数设为随机变量.
①求随机变量的概率;
②求的概率分布列以及数学期望.
【答案】(1);(2)①;②分布列见解析,.
【解析】(1)该校最终选地理的学生为事件,;
因此,该校最终选地理的学生为;
(2)①由题意可知,,所以,;
②由于,则,
,,
,
所以,随机变量的分布列如下表所示:
.
4.(2020·陕西渭南市)已知某植物种子每粒成功发芽的概率都为,某植物研究所分三个小组分别独立进行该种子的发芽试验,每次试验种一粒种子,每次试验结果相互独立.假设某次试验种子发芽,则称该次试验是成功的,如果种子没有发芽,则称该次试验是失败的.
(1)第一小组做了四次试验,求该小组恰有两次失败的概率;
(2)第二小组做了四次试验,设试验成功与失败的次数的差的绝对值为,求的分布列及数学期望.
【答案】(1);(2)答案见解析;.
【解析】(1)记“该小组有两次失败”为事件,
.
(2)由题意可知的可能取值为0,2,4.
,
,
.
故的分布列为:
0 2 4
.
考点二 超几何分布
【例2】(2020·全国高二单元测试)现对某高校16名篮球运动员在多次训练比赛中的得分进行统计,将每位运动员的平均成绩所得数据用频率分布直方图表示如下.(如:落在区间[10,15)内的频率/组距为0.0125)规定分数在[10,20),[20,30),[30,40)上的运动员分别为三级篮球运动员、二级篮球运动员、一级篮球运动员,现从这批篮球运动员中利用分层抽样的方法选出16名运动员作为该高校的篮球运动员代表.
(1)求a的值和选出篮球运动员代表中一级运动员的人数;
(2)若从篮球运动员代表中选出三人,求其中含有一级运动员人数X的分布列;
(3)若从该校篮球运动员中有放回地选三人,求其中含有一级运动员人数Y的期望.
【答案】(1)a=0.0250,4人;(2)答案见解析;(3).
【解析】(1)由频率分布直方图知:(0.0625+0.0500+0.0375+a+2×0.0125)×5=1,∴a=0.0250.
其中为一级运动员的概率为(0.012 5+0.037 5)×5=0.25,
∴选出篮球运动员代表中一级运动员为0.25×16=4人.
(2)由已知可得X的可能取值分别为0,1,2,3,
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
∴X的分布列为
X 0 1 2 3
P
(3)由已知得Y~B,
∴E(Y)=np=3×=,
∴含有一级运动员人数Y的期望为.
【一隅三反】
1.(2020·全国高二课时练习)新冠肺炎疫情期间,为了更有效地进行防控,各地学校都发出延期开学的通知.很多学校及老师为响应各地教育行政部门实行“停课不停学”的号召,让学生们在家通过收看网络直播的方式进行学习,已知高一某班共有学生21人,其中男生12人,女生9人.现采用分层抽样的方法从中抽取7人,测试他们对网络课程学习的效果,效果分为优秀和不优秀两种,优秀得2分,不优秀得1分.
(1)应抽取男生 女生各多少人?
(2)若抽取的7人中,4人的测试效果为优秀,3人为不优秀,现从这7人中随机抽取3人.
(i)用表示抽取的3人的得分之和,求随机变量x的分布列及数学期望;
(ii)设事件为“抽取的3人中,既有测试效果为优秀的,也有为不优秀的”,求事件发生的概率.
【答案】(1)人;(2)(i)分布列答案见解析,数学期望:;(ii).
【解析】(1)因为采用分层抽样的方法进行抽样,所以应抽取女生人,抽取男生人.
(2)(i)随机变量的所有可能取值为3,4,5,6.
, ,
,,
所以随机变量的分布列为
3 4 5 6
数学期望.
(ii)由(i)知,
故事件发生的概率为.
2.(2020·绵阳市·四川省绵阳江油中学)某校五四青年艺术节选拔主持人,现有来自高一年级参赛选手4名,其中男生2名;高二年级参赛选手4名,其中男生3名.从这8名参赛选手中随机选择4人组成搭档参赛.
(Ⅰ)设A为事件“选出的4人中恰有2名男生,且这2名男生来自同一个年级”,求事件A发生的概率;
(Ⅱ)设X为选出的4人中男生的人数,求随机变量X的分布列和数学期望.
【答案】(Ⅰ)(Ⅱ)分布列见解析,数学期望
【解析】(Ⅰ)由已知有,所以事件A发生的概率为.
(Ⅱ)随机变量X的所有可能取值为1,2,3,4,
所以随机变量X的分布列为
X
P
所以随机变量X的数学期望.
3.(2021·北京东城区)为了解学生自主学习期间完成数学套卷的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
(1)从这班学生中任选一名男生,一名女生,求这两名学生完成套卷数之和为4的概率?
(2)若从完成套卷数不少于4套的学生中任选4人,设选到的男学生人数为,求随机变量的分布列和数学期望;
(3)试判断男学生完成套卷数的方差与女学生完成套卷数的方差的大小(只需写出结论).
【答案】(1)(2)详见解析(3)
【解析】(1)设事件:从这个班级的学生中随机选取一名男生,一名女生,这两名学生完成套卷数之和为4,
由题意可知,.
(2)完成套卷数不少于4本的学生共8人,其中男学生人数为4人,故的取值为0,1,2,3,4.
由题意可得;
;
;
;
.
所以随机变量的分布列为
0 1 2 3 4
随机变量的均值.
(3).
考点三 二项分布与超几何分布综合运用
【例3】(2020·浙江台州市·高二期中)2020年五一期间,银泰百货举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有10个形状 大小完全相同的小球(其中红球2个,白球1个,黑球7个)的抽奖盒中,一次性摸出3个球其中奖规则为:若摸到2个红球和1个白球,享受免单优惠;若摸出2个红球和1个黑球则打5折;若摸出1个白球2个黑球,则打7折;其余情况不打折.方案二:从装有10个形状 大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率角度比较该顾客选择哪一种抽奖方案更合算?
【答案】(1);(2)选择第二种方案更合算.
【解析】(1)选择方案一若享受到免单优惠,则需要摸出三个红球,
设顾客享受到免单优惠为事件,则,
所以两位顾客均享受到免单的概率为;
(2)若选择方案一,设付款金额为元,则可能的取值为、、、.
,,
,.
故的分布列为,
所以(元).
若选择方案二,设摸到红球的个数为,付款金额为,则,
由已知可得,故,
所以(元).
因为,所以该顾客选择第二种抽奖方案更合算.
【一隅三反】
1.(2020·辽宁大连市)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;
(2)求在4次游戏中获奖次数的分布列及数学期望.
【答案】(1)①,②;(2)分布列见解析,.
【解析】(1)设“在1次游戏中摸出i个白球”为事件
①
②设“在1次游戏中获奖”为事件B,则,
又且A2,A3互斥,
所以
(2)由题意可知X的所有可能取值为0,1,2,3,4,
由(1),,
,
,
所以X的分布列是
X 0 1 2 3 4
P
显然 ,所以的数学期望E(X)=.
2.(2020·广东云浮市)甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题,按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大
【答案】(1) 甲、乙的分布列见解析;甲的数学期望2、乙的数学期望2; (2)甲通过面试的概率较大.
【解析】(1)设为甲正确完成面试题的数量,为乙正确完成面试题的数量,
依题意可得:,
∴,,,
∴X的分布列为:
X 1 2 3
P
∴.
,
∴,,
,,
∴Y的分布列为:
Y 0 1 2 3
P
∴.
(2),
,
∵,
∴甲发挥的稳定性更强,则甲通过面试的概率较大.
3.(2021·哈尔滨市)一批产品共10件,其中3件是不合格品,用下列两种不同方式从中随机抽取2件产品检验:
方法一:一次性随机抽取2件;
方法二:先随机抽取1件,放回后再随机抽取1件.
记方法一抽取的不合格产品数为.记方法二抽取的不合格产品数为.
(1)求两种抽取方式下,的概率分布列;
(2)比较两种抽取方式抽到的不合格品平均数的大小?并说明理由.
【答案】(1),的分布列见解析;(2)平均数相等,理由见解析.
【解析】(1)方法一中随机变量可取的值为0,1,2,且服从超几何分布,
于是;;
;
因此的频率分布可表示为下表:
0 1 2
方法二中随机变量可取的值为0,1,2,且服从二项分布,
于是;;
;
因此的频率分布可表示为下表:
0 1 2
(2)由(1)知,方法一中的数学期望为,
方法二中的数学期望为,
所以两种方式抽到的不合格品平均数相等.
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
人教版高中数学选择性必修第三册7.4二项分布与超几何分布同步训练(原卷版)
考法一 二项分布
【例1】(2020·全国高二课时练习)高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行 水平间隔相等的圆柱形铁钉(如图),并且每一排铁钉数目都比上一排多一个,一排中各个铁钉恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗铁钉间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.
(1)理论上,小球落入4号容器的概率是多少?
(2)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球的个数为,求的分布列.
【一隅三反】
1.(2020·重庆市第七中学校高二月考)若随机变量,则( )
A.2 B.3 C.4 D.5
2.(多选)(2020·全国高二单元测试)已知随机变量,若使的值最大,则k等于( )
A.5 B.6 C.7 D.8
3.(2020·江苏淮安市·淮阴中学高二期末)江苏实行的“新高考方案:”模式,其中统考科目:“”指语文、数学、外语三门,不分文理:学生根据高校的要求,结合自身特长兴趣,“”指首先在在物理、历史门科目中选择一门;“”指再从思想政治、地理、化学、生物门科目中选择门某校,根据统计选物理的学生占整个学生的;并且在选物理的条件下,选择地理的概率为;在选历史的条件下,选地理的概率为.
(1)求该校最终选地理的学生概率;
(2)该校甲、乙、丙三人选地理的人数设为随机变量.
①求随机变量的概率;
②求的概率分布列以及数学期望.
4.(2020·陕西渭南市)已知某植物种子每粒成功发芽的概率都为,某植物研究所分三个小组分别独立进行该种子的发芽试验,每次试验种一粒种子,每次试验结果相互独立.假设某次试验种子发芽,则称该次试验是成功的,如果种子没有发芽,则称该次试验是失败的.
(1)第一小组做了四次试验,求该小组恰有两次失败的概率;
(2)第二小组做了四次试验,设试验成功与失败的次数的差的绝对值为,求的分布列及数学期望.
考点二 超几何分布
【例2】(2020·全国高二单元测试)现对某高校16名篮球运动员在多次训练比赛中的得分进行统计,将每位运动员的平均成绩所得数据用频率分布直方图表示如下.(如:落在区间[10,15)内的频率/组距为0.0125)规定分数在[10,20),[20,30),[30,40)上的运动员分别为三级篮球运动员、二级篮球运动员、一级篮球运动员,现从这批篮球运动员中利用分层抽样的方法选出16名运动员作为该高校的篮球运动员代表.
(1)求a的值和选出篮球运动员代表中一级运动员的人数;
(2)若从篮球运动员代表中选出三人,求其中含有一级运动员人数X的分布列;
(3)若从该校篮球运动员中有放回地选三人,求其中含有一级运动员人数Y的期望.
【一隅三反】
1.(2020·全国高二课时练习)新冠肺炎疫情期间,为了更有效地进行防控,各地学校都发出延期开学的通知.很多学校及老师为响应各地教育行政部门实行“停课不停学”的号召,让学生们在家通过收看网络直播的方式进行学习,已知高一某班共有学生21人,其中男生12人,女生9人.现采用分层抽样的方法从中抽取7人,测试他们对网络课程学习的效果,效果分为优秀和不优秀两种,优秀得2分,不优秀得1分.
(1)应抽取男生 女生各多少人?
(2)若抽取的7人中,4人的测试效果为优秀,3人为不优秀,现从这7人中随机抽取3人.
(i)用表示抽取的3人的得分之和,求随机变量x的分布列及数学期望;
(ii)设事件为“抽取的3人中,既有测试效果为优秀的,也有为不优秀的”,求事件发生的概率.
2.(2020·绵阳市·四川省绵阳江油中学)某校五四青年艺术节选拔主持人,现有来自高一年级参赛选手4名,其中男生2名;高二年级参赛选手4名,其中男生3名.从这8名参赛选手中随机选择4人组成搭档参赛.
(Ⅰ)设A为事件“选出的4人中恰有2名男生,且这2名男生来自同一个年级”,求事件A发生的概率;
(Ⅱ)设X为选出的4人中男生的人数,求随机变量X的分布列和数学期望.
3.(2021·北京东城区)为了解学生自主学习期间完成数学套卷的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
(1)从这班学生中任选一名男生,一名女生,求这两名学生完成套卷数之和为4的概率?
(2)若从完成套卷数不少于4套的学生中任选4人,设选到的男学生人数为,求随机变量的分布列和数学期望;
(3)试判断男学生完成套卷数的方差与女学生完成套卷数的方差的大小(只需写出结论).
考点三 二项分布与超几何分布综合运用
【例3】(2020·浙江台州市·高二期中)2020年五一期间,银泰百货举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有10个形状 大小完全相同的小球(其中红球2个,白球1个,黑球7个)的抽奖盒中,一次性摸出3个球其中奖规则为:若摸到2个红球和1个白球,享受免单优惠;若摸出2个红球和1个黑球则打5折;若摸出1个白球2个黑球,则打7折;其余情况不打折.方案二:从装有10个形状 大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率角度比较该顾客选择哪一种抽奖方案更合算?
【一隅三反】
1.(2020·辽宁大连市)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;
(2)求在4次游戏中获奖次数的分布列及数学期望.
2.(2020·广东云浮市)甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题,按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大
3.(2021·哈尔滨市)一批产品共10件,其中3件是不合格品,用下列两种不同方式从中随机抽取2件产品检验:
方法一:一次性随机抽取2件;
方法二:先随机抽取1件,放回后再随机抽取1件.
记方法一抽取的不合格产品数为.记方法二抽取的不合格产品数为.
(1)求两种抽取方式下,的概率分布列;
(2)比较两种抽取方式抽到的不合格品平均数的大小?并说明理由.
人教版高中数学选择性必修第三册7.4二项分布与超几何分布同步训练(解析版)
考法一 二项分布
【例1】(2020·全国高二课时练习)高尔顿(钉)板是在一块竖起的木板上钉上一排排互相平行 水平间隔相等的圆柱形铁钉(如图),并且每一排铁钉数目都比上一排多一个,一排中各个铁钉恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗铁钉间隔的小球,当小球从两钉之间的间隙下落时,由于碰到下一排铁钉,它将以相等的可能性向左或向右落下,接着小球再通过两铁钉的间隙,又碰到下一排铁钉.如此继续下去,在最底层的5个出口处各放置一个容器接住小球.
(1)理论上,小球落入4号容器的概率是多少?
(2)一数学兴趣小组取3个小球进行试验,设其中落入4号容器的小球的个数为,求的分布列.
【答案】(1);(2)分布列答案见解析.
【解析】(1)记“小球落入4号容器”为事件,
若要小球落入4号容器,则需要在通过的四层中有三层向右,一层向左,
∴理论上,小球落入4号容器的概率.
(2)落入4号容器的小球的个数的所有可能取值为0,1,2,3,
,
,
,
,
的分布列为
0 1 2 3
【一隅三反】
1.(2020·重庆市第七中学校高二月考)若随机变量,则( )
A.2 B.3 C.4 D.5
【答案】D
【解析】因为,所以,所以.故选:D.
2.(多选)(2020·全国高二单元测试)已知随机变量,若使的值最大,则k等于( )
A.5 B.6 C.7 D.8
【答案】BC
【解析】令,得,
即当时,;
当时,;
当时,,
所以和的值最大.
故选:BC.
3.(2020·江苏淮安市·淮阴中学高二期末)江苏实行的“新高考方案:”模式,其中统考科目:“”指语文、数学、外语三门,不分文理:学生根据高校的要求,结合自身特长兴趣,“”指首先在在物理、历史门科目中选择一门;“”指再从思想政治、地理、化学、生物门科目中选择门某校,根据统计选物理的学生占整个学生的;并且在选物理的条件下,选择地理的概率为;在选历史的条件下,选地理的概率为.
(1)求该校最终选地理的学生概率;
(2)该校甲、乙、丙三人选地理的人数设为随机变量.
①求随机变量的概率;
②求的概率分布列以及数学期望.
【答案】(1);(2)①;②分布列见解析,.
【解析】(1)该校最终选地理的学生为事件,;
因此,该校最终选地理的学生为;
(2)①由题意可知,,所以,;
②由于,则,
,,
,
所以,随机变量的分布列如下表所示:
.
4.(2020·陕西渭南市)已知某植物种子每粒成功发芽的概率都为,某植物研究所分三个小组分别独立进行该种子的发芽试验,每次试验种一粒种子,每次试验结果相互独立.假设某次试验种子发芽,则称该次试验是成功的,如果种子没有发芽,则称该次试验是失败的.
(1)第一小组做了四次试验,求该小组恰有两次失败的概率;
(2)第二小组做了四次试验,设试验成功与失败的次数的差的绝对值为,求的分布列及数学期望.
【答案】(1);(2)答案见解析;.
【解析】(1)记“该小组有两次失败”为事件,
.
(2)由题意可知的可能取值为0,2,4.
,
,
.
故的分布列为:
0 2 4
.
考点二 超几何分布
【例2】(2020·全国高二单元测试)现对某高校16名篮球运动员在多次训练比赛中的得分进行统计,将每位运动员的平均成绩所得数据用频率分布直方图表示如下.(如:落在区间[10,15)内的频率/组距为0.0125)规定分数在[10,20),[20,30),[30,40)上的运动员分别为三级篮球运动员、二级篮球运动员、一级篮球运动员,现从这批篮球运动员中利用分层抽样的方法选出16名运动员作为该高校的篮球运动员代表.
(1)求a的值和选出篮球运动员代表中一级运动员的人数;
(2)若从篮球运动员代表中选出三人,求其中含有一级运动员人数X的分布列;
(3)若从该校篮球运动员中有放回地选三人,求其中含有一级运动员人数Y的期望.
【答案】(1)a=0.0250,4人;(2)答案见解析;(3).
【解析】(1)由频率分布直方图知:(0.0625+0.0500+0.0375+a+2×0.0125)×5=1,∴a=0.0250.
其中为一级运动员的概率为(0.012 5+0.037 5)×5=0.25,
∴选出篮球运动员代表中一级运动员为0.25×16=4人.
(2)由已知可得X的可能取值分别为0,1,2,3,
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
∴X的分布列为
X 0 1 2 3
P
(3)由已知得Y~B,
∴E(Y)=np=3×=,
∴含有一级运动员人数Y的期望为.
【一隅三反】
1.(2020·全国高二课时练习)新冠肺炎疫情期间,为了更有效地进行防控,各地学校都发出延期开学的通知.很多学校及老师为响应各地教育行政部门实行“停课不停学”的号召,让学生们在家通过收看网络直播的方式进行学习,已知高一某班共有学生21人,其中男生12人,女生9人.现采用分层抽样的方法从中抽取7人,测试他们对网络课程学习的效果,效果分为优秀和不优秀两种,优秀得2分,不优秀得1分.
(1)应抽取男生 女生各多少人?
(2)若抽取的7人中,4人的测试效果为优秀,3人为不优秀,现从这7人中随机抽取3人.
(i)用表示抽取的3人的得分之和,求随机变量x的分布列及数学期望;
(ii)设事件为“抽取的3人中,既有测试效果为优秀的,也有为不优秀的”,求事件发生的概率.
【答案】(1)人;(2)(i)分布列答案见解析,数学期望:;(ii).
【解析】(1)因为采用分层抽样的方法进行抽样,所以应抽取女生人,抽取男生人.
(2)(i)随机变量的所有可能取值为3,4,5,6.
, ,
,,
所以随机变量的分布列为
3 4 5 6
数学期望.
(ii)由(i)知,
故事件发生的概率为.
2.(2020·绵阳市·四川省绵阳江油中学)某校五四青年艺术节选拔主持人,现有来自高一年级参赛选手4名,其中男生2名;高二年级参赛选手4名,其中男生3名.从这8名参赛选手中随机选择4人组成搭档参赛.
(Ⅰ)设A为事件“选出的4人中恰有2名男生,且这2名男生来自同一个年级”,求事件A发生的概率;
(Ⅱ)设X为选出的4人中男生的人数,求随机变量X的分布列和数学期望.
【答案】(Ⅰ)(Ⅱ)分布列见解析,数学期望
【解析】(Ⅰ)由已知有,所以事件A发生的概率为.
(Ⅱ)随机变量X的所有可能取值为1,2,3,4,
所以随机变量X的分布列为
X
P
所以随机变量X的数学期望.
3.(2021·北京东城区)为了解学生自主学习期间完成数学套卷的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
(1)从这班学生中任选一名男生,一名女生,求这两名学生完成套卷数之和为4的概率?
(2)若从完成套卷数不少于4套的学生中任选4人,设选到的男学生人数为,求随机变量的分布列和数学期望;
(3)试判断男学生完成套卷数的方差与女学生完成套卷数的方差的大小(只需写出结论).
【答案】(1)(2)详见解析(3)
【解析】(1)设事件:从这个班级的学生中随机选取一名男生,一名女生,这两名学生完成套卷数之和为4,
由题意可知,.
(2)完成套卷数不少于4本的学生共8人,其中男学生人数为4人,故的取值为0,1,2,3,4.
由题意可得;
;
;
;
.
所以随机变量的分布列为
0 1 2 3 4
随机变量的均值.
(3).
考点三 二项分布与超几何分布综合运用
【例3】(2020·浙江台州市·高二期中)2020年五一期间,银泰百货举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.方案一:从装有10个形状 大小完全相同的小球(其中红球2个,白球1个,黑球7个)的抽奖盒中,一次性摸出3个球其中奖规则为:若摸到2个红球和1个白球,享受免单优惠;若摸出2个红球和1个黑球则打5折;若摸出1个白球2个黑球,则打7折;其余情况不打折.方案二:从装有10个形状 大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率角度比较该顾客选择哪一种抽奖方案更合算?
【答案】(1);(2)选择第二种方案更合算.
【解析】(1)选择方案一若享受到免单优惠,则需要摸出三个红球,
设顾客享受到免单优惠为事件,则,
所以两位顾客均享受到免单的概率为;
(2)若选择方案一,设付款金额为元,则可能的取值为、、、.
,,
,.
故的分布列为,
所以(元).
若选择方案二,设摸到红球的个数为,付款金额为,则,
由已知可得,故,
所以(元).
因为,所以该顾客选择第二种抽奖方案更合算.
【一隅三反】
1.(2020·辽宁大连市)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;
(2)求在4次游戏中获奖次数的分布列及数学期望.
【答案】(1)①,②;(2)分布列见解析,.
【解析】(1)设“在1次游戏中摸出i个白球”为事件
①
②设“在1次游戏中获奖”为事件B,则,
又且A2,A3互斥,
所以
(2)由题意可知X的所有可能取值为0,1,2,3,4,
由(1),,
,
,
所以X的分布列是
X 0 1 2 3 4
P
显然 ,所以的数学期望E(X)=.
2.(2020·广东云浮市)甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题,按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大
【答案】(1) 甲、乙的分布列见解析;甲的数学期望2、乙的数学期望2; (2)甲通过面试的概率较大.
【解析】(1)设为甲正确完成面试题的数量,为乙正确完成面试题的数量,
依题意可得:,
∴,,,
∴X的分布列为:
X 1 2 3
P
∴.
,
∴,,
,,
∴Y的分布列为:
Y 0 1 2 3
P
∴.
(2),
,
∵,
∴甲发挥的稳定性更强,则甲通过面试的概率较大.
3.(2021·哈尔滨市)一批产品共10件,其中3件是不合格品,用下列两种不同方式从中随机抽取2件产品检验:
方法一:一次性随机抽取2件;
方法二:先随机抽取1件,放回后再随机抽取1件.
记方法一抽取的不合格产品数为.记方法二抽取的不合格产品数为.
(1)求两种抽取方式下,的概率分布列;
(2)比较两种抽取方式抽到的不合格品平均数的大小?并说明理由.
【答案】(1),的分布列见解析;(2)平均数相等,理由见解析.
【解析】(1)方法一中随机变量可取的值为0,1,2,且服从超几何分布,
于是;;
;
因此的频率分布可表示为下表:
0 1 2
方法二中随机变量可取的值为0,1,2,且服从二项分布,
于是;;
;
因此的频率分布可表示为下表:
0 1 2
(2)由(1)知,方法一中的数学期望为,
方法二中的数学期望为,
所以两种方式抽到的不合格品平均数相等.
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
