探索与表达规律 北师大版数学 七年级上册(含答案)
文档属性
| 名称 | 探索与表达规律 北师大版数学 七年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 147.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 22:02:54 | ||
图片预览


文档简介
探索与表达规律 北师大版数学 七年级上册
一、填空题
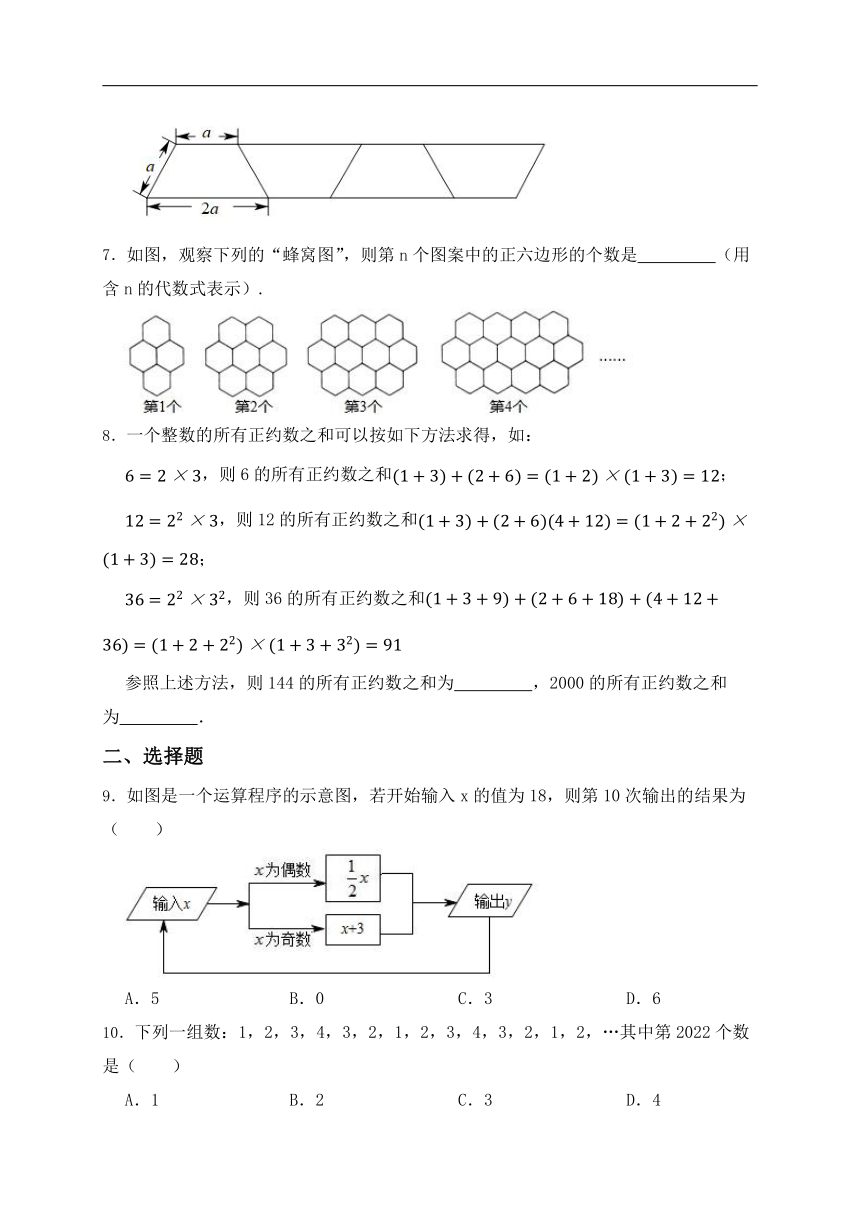
1.每一个多边形都可分割(分割方法如图)成若干个三角形.根据这种方法八边形可以分割成 个三角形.用此方法n边形能割成 个三角形.
2.观察下列单项式: , , , ,…,则第n个式子是 .
3.如图所示,圆的周长为4个单位长度,在圆的4等分点处标上字母、、、,先将圆周上的字母对应的点与数轴的数字1所对应的点重合,若将圆沿着数轴向右滚动,那么数轴上的数所对应的点将与圆周上的字母 重合.
4.观察下列等式:
,,, 第1个等式 第2个等式 第3个等式
按此规律,则第n个等式为 .
5.将相同的长方形卡片按如图方式摆放在一个直角上,每个长方形卡片长为2,宽为1,依此类推,摆放2023个时,实线部分长为 .
6.观察图形并填表(单位:)
梯形个数 1 2 3 4 5 6 … n
图形周长 …
7.如图,观察下列的“蜂窝图”,则第n个图案中的正六边形的个数是 (用含n的代数式表示).
8.一个整数的所有正约数之和可以按如下方法求得,如:
,则6的所有正约数之和;
,则12的所有正约数之和;
,则36的所有正约数之和
参照上述方法,则144的所有正约数之和为 ,2000的所有正约数之和为 .
二、选择题
9.如图是一个运算程序的示意图,若开始输入x的值为18,则第10次输出的结果为( )
A.5 B.0 C.3 D.6
10.下列一组数:1,2,3,4,3,2,1,2,3,4,3,2,1,2,…其中第2022个数是( )
A.1 B.2 C.3 D.4
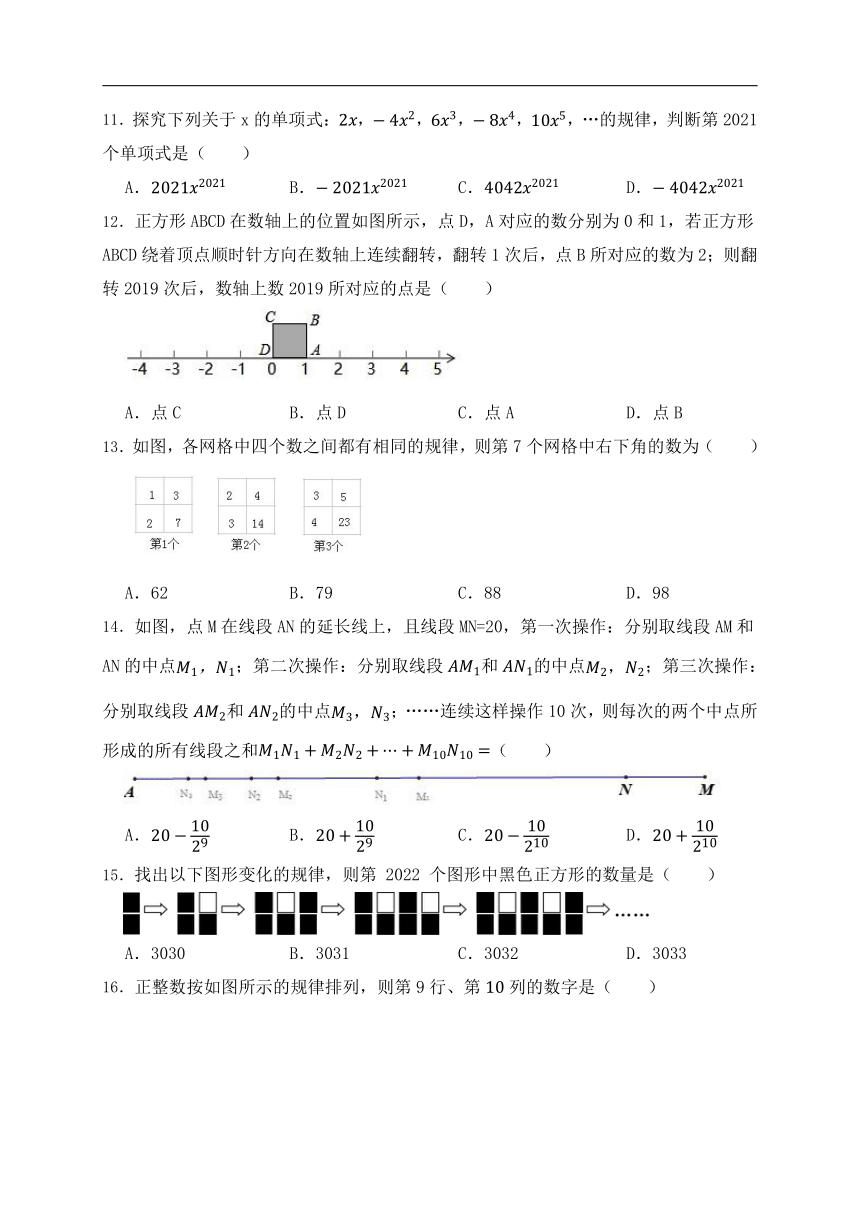
11.探究下列关于x的单项式:,,,,,…的规律,判断第2021个单项式是( )
A. B. C. D.
12.正方形ABCD在数轴上的位置如图所示,点D,A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2019次后,数轴上数2019所对应的点是( )
A.点C B.点D C.点A D.点B
13.如图,各网格中四个数之间都有相同的规律,则第7个网格中右下角的数为( )
A.62 B.79 C.88 D.98
14.如图,点M在线段AN的延长线上,且线段MN=20,第一次操作:分别取线段AM和AN的中点;第二次操作:分别取线段和的中点;第三次操作:分别取线段和的中点;……连续这样操作10次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
15.找出以下图形变化的规律,则第 2022 个图形中黑色正方形的数量是( )
A.3030 B.3031 C.3032 D.3033
16.正整数按如图所示的规律排列,则第9行、第列的数字是( )
A. B. C. D.
三、计算题
17.(1)﹣+(﹣)2+(π﹣3.14)0﹣()2;
(2)已知(2x﹣1)2﹣9=0,求x的值.
18.计算:
(1)1+2﹣3﹣4+5+6﹣7﹣8+…+2017+2018﹣2019﹣2020+2021;
(2)(﹣1)+(﹣2021)﹣(﹣4040)+(﹣1013)+(﹣1005).
四、综合题
19.阅读下列内容,并完成相关问题:
小明说:“我定义了一种新的运算,叫 (加乘)运算.”然后他写出了一些按照 (加乘)运算的运算法则进行运算的算式:
(+4)*(+2)=6;(-4)*(-3)=+7;…
(-5)*(+3)=-8;(+6)*(-7)=-13;…
(+8)*0=8;0*(-9)=9.…
小亮看了这些算式后说:“我知道你定义的 (加乘)运算的运算法则了.”请你帮助小亮完成下列问题:
(1)归纳 (加乘)运算的运算法则:
两数进行 (加乘)运算, .
特别地, 和任何数进行 (加乘)运算,或任何数和 进行 (加乘)运算,都得这个数的绝对值.
(2)若有理数的运算顺序适合 (加乘)运算,请直接写出结果:
①(-3) (-5)= ;
②(+3) (-5)= ;
③(-9) (+3) (-6)= ;
(3)试计算:[(-2)*(+3)]*[(-12)*0](括号的作用与它在有理数运算中的作用一致);
20.我们知道乌鸦喝水的故事.现在来做一个道理相同的游戏:如图,在圆柱形玻璃桶里已有定量的水,将大小相同的围棋棋子一个个慢慢投入其中.显然,在有水溢出之前,每投入一个棋子,桶里水位的高度都会有变化.根据如图信息,解答下列各题:
(1)投入第1个围棋子后,水位上升了 ,此时桶里的水位高度达到了 ;
(2)设投入了n个棋子,没有水溢出.用n表示此时桶里水位的高度;
(3)小亮认为投入个棋子,正好可使水位达到桶的高度.你同意他的观点吗?说说理由.
21.观察算式:
;;;,…
(1)请根据你发现的规律填空:( )2;
(2)用含n的等式表示上面的规律: ;(n为正整数)
(3)利用找到的规律解决下面的问题:
计算:.
答案解析部分
1.【答案】6;(n﹣2)
2.【答案】
3.【答案】C
4.【答案】n2-(n-1)2=2n-1
5.【答案】5058
6.【答案】17a;2a+3na
7.【答案】
8.【答案】403;4836
9.【答案】C
10.【答案】B
11.【答案】C
12.【答案】A
13.【答案】B
14.【答案】A
15.【答案】D
16.【答案】A
17.【答案】(1)解:原式,
,
;
(2)解:,
,
或,
或.
18.【答案】(1)解:原式=1+(2﹣3)+(﹣4+5)+(6﹣7)+(﹣8+9)+…+(2014﹣2015)+(﹣2016+2017)+(2018﹣2019)﹣2020+2021
=1﹣1﹣2020+2021
=1.
(2)解:原式=
=[﹣1+(﹣2021)+4040+(﹣1013)+(﹣1005)]+
=
=﹣.
19.【答案】(1)同号得正、异号得负,把绝对值相加
(2)8;-8;19
(3)解:原式=( 5)*12= 17.
20.【答案】(1)0.25;12.25
(2)解:∵每增加一个围棋子,水位上升,
故桶里水位的高度为,
(3)解:同意.
理由:∵当时,,
∴正好使水位达到桶的高度.
21.【答案】(1)7
(2)n (n+2)+1=(n+1)2
(3)解:原式=
=.
一、填空题
1.每一个多边形都可分割(分割方法如图)成若干个三角形.根据这种方法八边形可以分割成 个三角形.用此方法n边形能割成 个三角形.
2.观察下列单项式: , , , ,…,则第n个式子是 .
3.如图所示,圆的周长为4个单位长度,在圆的4等分点处标上字母、、、,先将圆周上的字母对应的点与数轴的数字1所对应的点重合,若将圆沿着数轴向右滚动,那么数轴上的数所对应的点将与圆周上的字母 重合.
4.观察下列等式:
,,, 第1个等式 第2个等式 第3个等式
按此规律,则第n个等式为 .
5.将相同的长方形卡片按如图方式摆放在一个直角上,每个长方形卡片长为2,宽为1,依此类推,摆放2023个时,实线部分长为 .
6.观察图形并填表(单位:)
梯形个数 1 2 3 4 5 6 … n
图形周长 …
7.如图,观察下列的“蜂窝图”,则第n个图案中的正六边形的个数是 (用含n的代数式表示).
8.一个整数的所有正约数之和可以按如下方法求得,如:
,则6的所有正约数之和;
,则12的所有正约数之和;
,则36的所有正约数之和
参照上述方法,则144的所有正约数之和为 ,2000的所有正约数之和为 .
二、选择题
9.如图是一个运算程序的示意图,若开始输入x的值为18,则第10次输出的结果为( )
A.5 B.0 C.3 D.6
10.下列一组数:1,2,3,4,3,2,1,2,3,4,3,2,1,2,…其中第2022个数是( )
A.1 B.2 C.3 D.4
11.探究下列关于x的单项式:,,,,,…的规律,判断第2021个单项式是( )
A. B. C. D.
12.正方形ABCD在数轴上的位置如图所示,点D,A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2019次后,数轴上数2019所对应的点是( )
A.点C B.点D C.点A D.点B
13.如图,各网格中四个数之间都有相同的规律,则第7个网格中右下角的数为( )
A.62 B.79 C.88 D.98
14.如图,点M在线段AN的延长线上,且线段MN=20,第一次操作:分别取线段AM和AN的中点;第二次操作:分别取线段和的中点;第三次操作:分别取线段和的中点;……连续这样操作10次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
15.找出以下图形变化的规律,则第 2022 个图形中黑色正方形的数量是( )
A.3030 B.3031 C.3032 D.3033
16.正整数按如图所示的规律排列,则第9行、第列的数字是( )
A. B. C. D.
三、计算题
17.(1)﹣+(﹣)2+(π﹣3.14)0﹣()2;
(2)已知(2x﹣1)2﹣9=0,求x的值.
18.计算:
(1)1+2﹣3﹣4+5+6﹣7﹣8+…+2017+2018﹣2019﹣2020+2021;
(2)(﹣1)+(﹣2021)﹣(﹣4040)+(﹣1013)+(﹣1005).
四、综合题
19.阅读下列内容,并完成相关问题:
小明说:“我定义了一种新的运算,叫 (加乘)运算.”然后他写出了一些按照 (加乘)运算的运算法则进行运算的算式:
(+4)*(+2)=6;(-4)*(-3)=+7;…
(-5)*(+3)=-8;(+6)*(-7)=-13;…
(+8)*0=8;0*(-9)=9.…
小亮看了这些算式后说:“我知道你定义的 (加乘)运算的运算法则了.”请你帮助小亮完成下列问题:
(1)归纳 (加乘)运算的运算法则:
两数进行 (加乘)运算, .
特别地, 和任何数进行 (加乘)运算,或任何数和 进行 (加乘)运算,都得这个数的绝对值.
(2)若有理数的运算顺序适合 (加乘)运算,请直接写出结果:
①(-3) (-5)= ;
②(+3) (-5)= ;
③(-9) (+3) (-6)= ;
(3)试计算:[(-2)*(+3)]*[(-12)*0](括号的作用与它在有理数运算中的作用一致);
20.我们知道乌鸦喝水的故事.现在来做一个道理相同的游戏:如图,在圆柱形玻璃桶里已有定量的水,将大小相同的围棋棋子一个个慢慢投入其中.显然,在有水溢出之前,每投入一个棋子,桶里水位的高度都会有变化.根据如图信息,解答下列各题:
(1)投入第1个围棋子后,水位上升了 ,此时桶里的水位高度达到了 ;
(2)设投入了n个棋子,没有水溢出.用n表示此时桶里水位的高度;
(3)小亮认为投入个棋子,正好可使水位达到桶的高度.你同意他的观点吗?说说理由.
21.观察算式:
;;;,…
(1)请根据你发现的规律填空:( )2;
(2)用含n的等式表示上面的规律: ;(n为正整数)
(3)利用找到的规律解决下面的问题:
计算:.
答案解析部分
1.【答案】6;(n﹣2)
2.【答案】
3.【答案】C
4.【答案】n2-(n-1)2=2n-1
5.【答案】5058
6.【答案】17a;2a+3na
7.【答案】
8.【答案】403;4836
9.【答案】C
10.【答案】B
11.【答案】C
12.【答案】A
13.【答案】B
14.【答案】A
15.【答案】D
16.【答案】A
17.【答案】(1)解:原式,
,
;
(2)解:,
,
或,
或.
18.【答案】(1)解:原式=1+(2﹣3)+(﹣4+5)+(6﹣7)+(﹣8+9)+…+(2014﹣2015)+(﹣2016+2017)+(2018﹣2019)﹣2020+2021
=1﹣1﹣2020+2021
=1.
(2)解:原式=
=[﹣1+(﹣2021)+4040+(﹣1013)+(﹣1005)]+
=
=﹣.
19.【答案】(1)同号得正、异号得负,把绝对值相加
(2)8;-8;19
(3)解:原式=( 5)*12= 17.
20.【答案】(1)0.25;12.25
(2)解:∵每增加一个围棋子,水位上升,
故桶里水位的高度为,
(3)解:同意.
理由:∵当时,,
∴正好使水位达到桶的高度.
21.【答案】(1)7
(2)n (n+2)+1=(n+1)2
(3)解:原式=
=.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
