人教版高中数学选择性必修第三册6.3 二项式定理 同步训练(含答案)
文档属性
| 名称 | 人教版高中数学选择性必修第三册6.3 二项式定理 同步训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-15 21:09:36 | ||
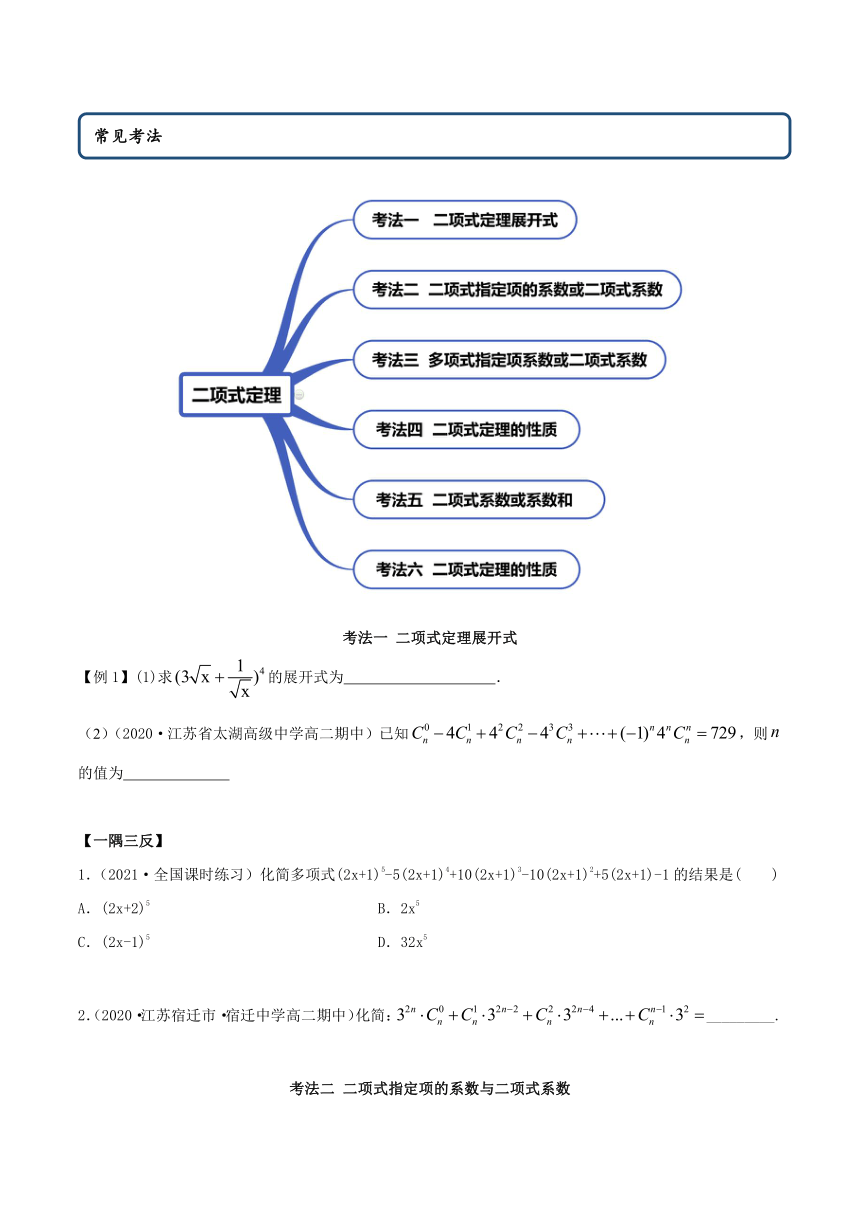
图片预览




文档简介
本资料分享自高中数学同步资源大全QQ群483122854 专注收集同步资源期待你的加入与分享
人教版高中数学选择性必修第三册6.3 二项式定理 同步训练(原卷版)
考法一 二项式定理展开式
【例1】(1)求的展开式为 .
(2)(2020·江苏省太湖高级中学高二期中)已知,则的值为
【一隅三反】
1.(2021·全国课时练习)化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1的结果是( )
A.(2x+2)5 B.2x5
C.(2x-1)5 D.32x5
2.(2020·江苏宿迁市·宿迁中学高二期中)化简:_________.
考法二 二项式指定项的系数与二项式系数
【例2】(1)(2020·全国高二单元测试)在(x-)10的展开式中,x6的系数是
(2)(2020·广东佛山市·高二期末)二项式的展开式中常数项是______(用数字作答)
(3)(2020·安徽省蚌埠第三中学高二月考)的有理项共有 项
【一隅三反】
1.(2020·北京市鲁迅中学高二月考)二项式的展开式中的常数项是_______.(用数字作答)
2.(2021·上海青浦区)在二项展开式中,常数项是_______.
3..(2020·青海西宁市)若的展开式中的系数为7,则实数=______.
4.(2020·梁河县)已知的展开式的常数项是第7项,则________.
考法三 多项式系数或二项式系数
【例3】(1)(2020·福建三明市·高二期末)的展开式中常数项是( )
A.-252 B.-220 C.220 D.252
(2).(2021·四川成都市)若的展开式中常数项为,则( )
A. B. C. D.
【一隅三反】
1.(2020·全国高三专题练习)展开式中常数项为( ).
A.11 B. C.8 D.
2.(2020·全国高三专题练习)的展开式中常数项为( )
A. B. C. D.
3.(2020·河南商丘市)的展开式的常数项为( )
A.6 B.10 C.15 D.16
4.(2020·枣庄市第三中学高二月考)在的展开式中,x2项的系数为( )
A.30 B.45 C.60 D.90
5.(2020·全国高二专题练习)若的展开式中的系数为,则等于( )
A. B. C.1 D.2
考法四 二项式定理的性质
【例2】(1)(多选)(2020·全国高二单元测试)的展开式中二项式系数最大的项是( )
A.第5项 B.第6项
C.第7项 D.第8项
(2)(2020·山东省桓台第一中学高二期中)(多选)二项式的展开式中,系数最大的项为( ).
A.第五项 B.第六项 C.第七项 D.第八项
(3)(2020·绵阳市·四川省绵阳江油中学高二开学考试)若的展开式中只有第项的二项式系数最大,则展开式中含项的系数是
A. B.
C. D.
【一隅三反】
1.(2020·辽宁沈阳市·高二期中)在的二项展开式中,若只有第5项的二项式系数最大,则的二项展开式中的常数项为( )
A.960 B.1120 C.-560 D.-960
2.(2021·湖南常德市)的展开式中各项系数的和为2,则该展开式中常数项为( )
A. B. C.10 D.20
3.(多选)(2020·三亚华侨学校高二开学考试)已知的展开式中第5项的二项式系数最大,则n的值可以为( )
A.7 B.8 C.9 D.10
4.(2020·全国高二课时练习)已知展开式中各项系数的和为m,且,求展开式中二项式系数最大的项的系数 .
5.(2020·重庆市第七中学校高二月考)二项式 的展开式中,二项式系数最大的项是第4项,则其展开式中的常数项是_________.
考法五 二项式系数或系数和
【例5】(2020·安徽省泗县)若.
求:(1);
(2);
(3).
【一隅三反】
1.(2020·北京朝阳区·高二期末)在的二项展开式中,二项式系数之和为___________;所有项的系数之和为_______.
2.(2020·全国高二单元测试)若(-x)10=a0+a1x+a2x2+…+a10x10,则(a0+a2+…+a10)2-(a1+a3+…+a9)2=
3.(2020·福建厦门市·厦门双十中学高二期中)已知 ,则_____.
4.(2020·宁县第二中学高二期中)设展开式中只有第1010项的二项式系数最大.
(1)求n;
(2)求;
(3)求..
考法六 二项式定理运用
【例6】(1)(2020·上海市七宝中学高二期中)除以100的余数是________
(2)(2020·全国高二单元测试)的计算结果精确到0.01的近似值是_________
【一隅三反】
1.(2020·四川棠湖中学高二月考)已知能够被15整除,则________.
2.(2020·江苏泰州市·泰州中学高二期中)被除所得的余数是_____________.
(2021·河北保定市)的计算结果精确到0.001的近似值是
人教版高中数学选择性必修第三册6.3 二项式定理 同步训练(解析版)
考法一 二项式定理展开式
【例1】(1)求的展开式为 .
(2)(2020·江苏省太湖高级中学高二期中)已知,则的值为
【答案】(1)++54+108x+81x2
【解析】(1)方法一 4=(3)4+C(3)3·+C(3)22+C(3)3+C4=81x2+108x+54++.
方法二 4=4=(1+3x)4=·[1+C·3x+C(3x)2+C(3x)3+C(3x)4]=(1+12x+54x2+108x3+81x4)=++54+108x+81x2.
(2)由得
则,即,解得.
【一隅三反】
1.(2021·全国课时练习)化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1的结果是( )
A.(2x+2)5 B.2x5
C.(2x-1)5 D.32x5
【答案】D
【解析】依题意可知,多项式的每一项都可看作,故为的展开式,化简.故选D.
2.(2020·江苏宿迁市·宿迁中学高二期中)化简:_________.
【答案】
【解析】
则
所以故答案为:.
考法二 二项式指定项的系数与二项式系数
【例2】(1)(2020·全国高二单元测试)在(x-)10的展开式中,x6的系数是
(2)(2020·广东佛山市·高二期末)二项式的展开式中常数项是______(用数字作答)
(3)(2020·安徽省蚌埠第三中学高二月考)的有理项共有 项
【答案】(1)9(2)70(3)6
【解析】(1)由Tk+1=x10-k(-)k,令10-k=6,解得k=4,∴系数为(-)4=9
(2)二项式的展开式的通项公式,令,得,则常数项为,故答案为:70
(3)的通项公式为:,
,
,
,
所以有理项共有6项,故选:C
【一隅三反】
1.(2020·北京市鲁迅中学高二月考)二项式的展开式中的常数项是_______.(用数字作答)
【答案】60
【解析】有题意可得,二项式展开式的通项为:
令可得 ,此时.
2.(2021·上海青浦区)在二项展开式中,常数项是_______.
【答案】60
【解析】展开式的通项公式是,当时,
.故答案为60
3..(2020·青海西宁市)若的展开式中的系数为7,则实数=______.
【答案】
【解析】根据二项展开式的通项公式可得:,
令,可得,,解得:,故答案为:
4.(2020·梁河县)已知的展开式的常数项是第7项,则________.
【答案】8
【解析】根据题意,可知第7项为,而常数项是第7项,则
,故.故答案为:8.
考法三 多项式系数或二项式系数
【例3】(1)(2020·福建三明市·高二期末)的展开式中常数项是( )
A.-252 B.-220 C.220 D.252
(2).(2021·四川成都市)若的展开式中常数项为,则( )
A. B. C. D.
【答案】(1)A(2)C
【解析】(1)由,
可得二项式的展开式通项为,
令,解得,所以展开式的常数项为.故选:A.
(2)的展开式的通项公式为:,显然,为奇数,
若求展开式的常数项,,解得
故的展开式的常数项等于:故选:C.
【一隅三反】
1.(2020·全国高三专题练习)展开式中常数项为( ).
A.11 B. C.8 D.
【答案】B
【解析】将看成一个整体,展开得到:
的展开式为:取
当时, 系数为: 当时, 系数为:
常数项为 故答案选B
2.(2020·全国高三专题练习)的展开式中常数项为( )
A. B. C. D.
【答案】C
【解析】 的通项为, ,根据式子可知当 或 时有常数项,令 ; 令;故所求常数项为 ,故选C.
3.(2020·河南商丘市)的展开式的常数项为( )
A.6 B.10 C.15 D.16
【答案】D
【解析】由题意得的展开式的通项为,
令,则,所以的展开式的常数项为.故选:D.
4.(2020·枣庄市第三中学高二月考)在的展开式中,x2项的系数为( )
A.30 B.45 C.60 D.90
【答案】B
【解析】在的展开式中,通项公式为Tr+1 .
对于,通项公式为Tk+1 xr﹣2021k,k≤r,r、k∈N,r≤10.
令r﹣2021k=2,可得r=2+2021k,故k=0,r=2,故x2项的系数为 45,故选:B.
5.(2020·全国高二专题练习)若的展开式中的系数为,则等于( )
A. B. C.1 D.2
【答案】D
【解析】将题中所给式子可化为
根据二项式定理展开式通项为,的通项为
令 解得
所以的项为令解得
所以的项为
综上可知, 的系数为 解得 故选:D
考法四 二项式定理的性质
【例2】(1)(多选)(2020·全国高二单元测试)的展开式中二项式系数最大的项是( )
A.第5项 B.第6项
C.第7项 D.第8项
(2)(2020·山东省桓台第一中学高二期中)(多选)二项式的展开式中,系数最大的项为( ).
A.第五项 B.第六项 C.第七项 D.第八项
(3)(2020·绵阳市·四川省绵阳江油中学高二开学考试)若的展开式中只有第项的二项式系数最大,则展开式中含项的系数是
A. B.
C. D.
【答案】(1)BC(2)BC(3)D
【解析】(1)因为n=11为奇数,所以展开式中第项和第项,即第6项和第7项的二项式系数相等,且最大.故选:BC
(2)二项式的展开式中,每项的系数与二项式系数相等,共有12项
所以系数最大的项为第六项和第七项故选:BC
(3)∵的展开式中只有第项的二项式系数最大,∴为偶数,展开式共有项,则.
的展开式的通项公式为,令,得.
∴展开式中含项的系数是,故选D.
【一隅三反】
1.(2020·辽宁沈阳市·高二期中)在的二项展开式中,若只有第5项的二项式系数最大,则的二项展开式中的常数项为( )
A.960 B.1120 C.-560 D.-960
【答案】B
【解析】在(x﹣1)n(n∈N+)的二项展开式中,若只有第5项的二项式系数最大,则n=8,
则=的二项展开式的通项公式为Tr+1= 28﹣r (﹣1)r x4﹣r,
令4﹣r=0,求得r=4,可得展开式中的常数项为 24 (﹣1)4=1120,故选B.
2.(2021·湖南常德市)的展开式中各项系数的和为2,则该展开式中常数项为( )
A. B. C.10 D.20
【答案】C
【解析】由已知,当时,即,所以展开式中常数项为,故选.
3.(多选)(2020·三亚华侨学校高二开学考试)已知的展开式中第5项的二项式系数最大,则n的值可以为( )
A.7 B.8 C.9 D.10
【答案】ABC
【解析】∵已知的展开式中第5项的二项式系数最大,则或n=8或n=9故选:ABC.
4.(2020·全国高二课时练习)已知展开式中各项系数的和为m,且,求展开式中二项式系数最大的项的系数 .
【答案】59136
【解析】设,令,得,
所以,则展开式中有13项,且中间一项(第7项)的二项式系数最大,
该项为.故所求的系数为59136.
5.(2020·重庆市第七中学校高二月考)二项式 的展开式中,二项式系数最大的项是第4项,则其展开式中的常数项是_________.
【答案】-20
【解析】由题意知,展开式中有7项,.因为
令,得,所以常数项为.
考法五 二项式系数或系数和
【例5】(2020·安徽省泗县)若.
求:(1);
(2);
(3).
【答案】(1)27;(2)14;(3)27.
【解析】(1)令,可得,
∴.①
(2)令可得,
∴.②
由①②得,
∴.
(3)由题意得二项式展开式的通项为,
∴每项的系数,
∴.
【一隅三反】
1.(2020·北京朝阳区·高二期末)在的二项展开式中,二项式系数之和为___________;所有项的系数之和为_______.
【答案】
【解析】根据二项展开式的性质,展开式的二项式系数之和为,
令可得所有项的系数之和为,故答案为:,
2.(2020·全国高二单元测试)若(-x)10=a0+a1x+a2x2+…+a10x10,则(a0+a2+…+a10)2-(a1+a3+…+a9)2=
【答案】1
【解析】令,得,令,得,
.故选:A.
3.(2020·福建厦门市·厦门双十中学高二期中)已知 ,则_____.
【答案】
【解析】对等式两边求导,得,令,则.
4.(2020·宁县第二中学高二期中)设展开式中只有第1010项的二项式系数最大.
(1)求n;
(2)求;
(3)求..
【答案】(1)2018;(2);(3)-1.
【解析】(1)由二项式系数的对称性,
(2)
(3)令 ,得,
令,得,故.
考法六 二项式定理运用
【例6】(1)(2020·上海市七宝中学高二期中)除以100的余数是________
(2)(2020·全国高二单元测试)的计算结果精确到0.01的近似值是_________
【答案】(1)41(2)1.34
【解析】(1)
即除以100的余数为.故答案为:.
(2)故答案为:
【一隅三反】
1.(2020·四川棠湖中学高二月考)已知能够被15整除,则________.
【答案】14
【解析】由题可知,
所以,
而75能被15整除,要使能够被15整除,只需能被15整除即可,
所以,解得:.故答案为:14.
2.(2020·江苏泰州市·泰州中学高二期中)被除所得的余数是_____________.
【答案】1
【解析】因为
,
所以转化为求被除所得的余数,
因为,所以被除所得的余数是1,故答案为:1
3.(2021·河北保定市)的计算结果精确到0.001的近似值是
【答案】0.941
【解析】
故选B
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
人教版高中数学选择性必修第三册6.3 二项式定理 同步训练(原卷版)
考法一 二项式定理展开式
【例1】(1)求的展开式为 .
(2)(2020·江苏省太湖高级中学高二期中)已知,则的值为
【一隅三反】
1.(2021·全国课时练习)化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1的结果是( )
A.(2x+2)5 B.2x5
C.(2x-1)5 D.32x5
2.(2020·江苏宿迁市·宿迁中学高二期中)化简:_________.
考法二 二项式指定项的系数与二项式系数
【例2】(1)(2020·全国高二单元测试)在(x-)10的展开式中,x6的系数是
(2)(2020·广东佛山市·高二期末)二项式的展开式中常数项是______(用数字作答)
(3)(2020·安徽省蚌埠第三中学高二月考)的有理项共有 项
【一隅三反】
1.(2020·北京市鲁迅中学高二月考)二项式的展开式中的常数项是_______.(用数字作答)
2.(2021·上海青浦区)在二项展开式中,常数项是_______.
3..(2020·青海西宁市)若的展开式中的系数为7,则实数=______.
4.(2020·梁河县)已知的展开式的常数项是第7项,则________.
考法三 多项式系数或二项式系数
【例3】(1)(2020·福建三明市·高二期末)的展开式中常数项是( )
A.-252 B.-220 C.220 D.252
(2).(2021·四川成都市)若的展开式中常数项为,则( )
A. B. C. D.
【一隅三反】
1.(2020·全国高三专题练习)展开式中常数项为( ).
A.11 B. C.8 D.
2.(2020·全国高三专题练习)的展开式中常数项为( )
A. B. C. D.
3.(2020·河南商丘市)的展开式的常数项为( )
A.6 B.10 C.15 D.16
4.(2020·枣庄市第三中学高二月考)在的展开式中,x2项的系数为( )
A.30 B.45 C.60 D.90
5.(2020·全国高二专题练习)若的展开式中的系数为,则等于( )
A. B. C.1 D.2
考法四 二项式定理的性质
【例2】(1)(多选)(2020·全国高二单元测试)的展开式中二项式系数最大的项是( )
A.第5项 B.第6项
C.第7项 D.第8项
(2)(2020·山东省桓台第一中学高二期中)(多选)二项式的展开式中,系数最大的项为( ).
A.第五项 B.第六项 C.第七项 D.第八项
(3)(2020·绵阳市·四川省绵阳江油中学高二开学考试)若的展开式中只有第项的二项式系数最大,则展开式中含项的系数是
A. B.
C. D.
【一隅三反】
1.(2020·辽宁沈阳市·高二期中)在的二项展开式中,若只有第5项的二项式系数最大,则的二项展开式中的常数项为( )
A.960 B.1120 C.-560 D.-960
2.(2021·湖南常德市)的展开式中各项系数的和为2,则该展开式中常数项为( )
A. B. C.10 D.20
3.(多选)(2020·三亚华侨学校高二开学考试)已知的展开式中第5项的二项式系数最大,则n的值可以为( )
A.7 B.8 C.9 D.10
4.(2020·全国高二课时练习)已知展开式中各项系数的和为m,且,求展开式中二项式系数最大的项的系数 .
5.(2020·重庆市第七中学校高二月考)二项式 的展开式中,二项式系数最大的项是第4项,则其展开式中的常数项是_________.
考法五 二项式系数或系数和
【例5】(2020·安徽省泗县)若.
求:(1);
(2);
(3).
【一隅三反】
1.(2020·北京朝阳区·高二期末)在的二项展开式中,二项式系数之和为___________;所有项的系数之和为_______.
2.(2020·全国高二单元测试)若(-x)10=a0+a1x+a2x2+…+a10x10,则(a0+a2+…+a10)2-(a1+a3+…+a9)2=
3.(2020·福建厦门市·厦门双十中学高二期中)已知 ,则_____.
4.(2020·宁县第二中学高二期中)设展开式中只有第1010项的二项式系数最大.
(1)求n;
(2)求;
(3)求..
考法六 二项式定理运用
【例6】(1)(2020·上海市七宝中学高二期中)除以100的余数是________
(2)(2020·全国高二单元测试)的计算结果精确到0.01的近似值是_________
【一隅三反】
1.(2020·四川棠湖中学高二月考)已知能够被15整除,则________.
2.(2020·江苏泰州市·泰州中学高二期中)被除所得的余数是_____________.
(2021·河北保定市)的计算结果精确到0.001的近似值是
人教版高中数学选择性必修第三册6.3 二项式定理 同步训练(解析版)
考法一 二项式定理展开式
【例1】(1)求的展开式为 .
(2)(2020·江苏省太湖高级中学高二期中)已知,则的值为
【答案】(1)++54+108x+81x2
【解析】(1)方法一 4=(3)4+C(3)3·+C(3)22+C(3)3+C4=81x2+108x+54++.
方法二 4=4=(1+3x)4=·[1+C·3x+C(3x)2+C(3x)3+C(3x)4]=(1+12x+54x2+108x3+81x4)=++54+108x+81x2.
(2)由得
则,即,解得.
【一隅三反】
1.(2021·全国课时练习)化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1的结果是( )
A.(2x+2)5 B.2x5
C.(2x-1)5 D.32x5
【答案】D
【解析】依题意可知,多项式的每一项都可看作,故为的展开式,化简.故选D.
2.(2020·江苏宿迁市·宿迁中学高二期中)化简:_________.
【答案】
【解析】
则
所以故答案为:.
考法二 二项式指定项的系数与二项式系数
【例2】(1)(2020·全国高二单元测试)在(x-)10的展开式中,x6的系数是
(2)(2020·广东佛山市·高二期末)二项式的展开式中常数项是______(用数字作答)
(3)(2020·安徽省蚌埠第三中学高二月考)的有理项共有 项
【答案】(1)9(2)70(3)6
【解析】(1)由Tk+1=x10-k(-)k,令10-k=6,解得k=4,∴系数为(-)4=9
(2)二项式的展开式的通项公式,令,得,则常数项为,故答案为:70
(3)的通项公式为:,
,
,
,
所以有理项共有6项,故选:C
【一隅三反】
1.(2020·北京市鲁迅中学高二月考)二项式的展开式中的常数项是_______.(用数字作答)
【答案】60
【解析】有题意可得,二项式展开式的通项为:
令可得 ,此时.
2.(2021·上海青浦区)在二项展开式中,常数项是_______.
【答案】60
【解析】展开式的通项公式是,当时,
.故答案为60
3..(2020·青海西宁市)若的展开式中的系数为7,则实数=______.
【答案】
【解析】根据二项展开式的通项公式可得:,
令,可得,,解得:,故答案为:
4.(2020·梁河县)已知的展开式的常数项是第7项,则________.
【答案】8
【解析】根据题意,可知第7项为,而常数项是第7项,则
,故.故答案为:8.
考法三 多项式系数或二项式系数
【例3】(1)(2020·福建三明市·高二期末)的展开式中常数项是( )
A.-252 B.-220 C.220 D.252
(2).(2021·四川成都市)若的展开式中常数项为,则( )
A. B. C. D.
【答案】(1)A(2)C
【解析】(1)由,
可得二项式的展开式通项为,
令,解得,所以展开式的常数项为.故选:A.
(2)的展开式的通项公式为:,显然,为奇数,
若求展开式的常数项,,解得
故的展开式的常数项等于:故选:C.
【一隅三反】
1.(2020·全国高三专题练习)展开式中常数项为( ).
A.11 B. C.8 D.
【答案】B
【解析】将看成一个整体,展开得到:
的展开式为:取
当时, 系数为: 当时, 系数为:
常数项为 故答案选B
2.(2020·全国高三专题练习)的展开式中常数项为( )
A. B. C. D.
【答案】C
【解析】 的通项为, ,根据式子可知当 或 时有常数项,令 ; 令;故所求常数项为 ,故选C.
3.(2020·河南商丘市)的展开式的常数项为( )
A.6 B.10 C.15 D.16
【答案】D
【解析】由题意得的展开式的通项为,
令,则,所以的展开式的常数项为.故选:D.
4.(2020·枣庄市第三中学高二月考)在的展开式中,x2项的系数为( )
A.30 B.45 C.60 D.90
【答案】B
【解析】在的展开式中,通项公式为Tr+1 .
对于,通项公式为Tk+1 xr﹣2021k,k≤r,r、k∈N,r≤10.
令r﹣2021k=2,可得r=2+2021k,故k=0,r=2,故x2项的系数为 45,故选:B.
5.(2020·全国高二专题练习)若的展开式中的系数为,则等于( )
A. B. C.1 D.2
【答案】D
【解析】将题中所给式子可化为
根据二项式定理展开式通项为,的通项为
令 解得
所以的项为令解得
所以的项为
综上可知, 的系数为 解得 故选:D
考法四 二项式定理的性质
【例2】(1)(多选)(2020·全国高二单元测试)的展开式中二项式系数最大的项是( )
A.第5项 B.第6项
C.第7项 D.第8项
(2)(2020·山东省桓台第一中学高二期中)(多选)二项式的展开式中,系数最大的项为( ).
A.第五项 B.第六项 C.第七项 D.第八项
(3)(2020·绵阳市·四川省绵阳江油中学高二开学考试)若的展开式中只有第项的二项式系数最大,则展开式中含项的系数是
A. B.
C. D.
【答案】(1)BC(2)BC(3)D
【解析】(1)因为n=11为奇数,所以展开式中第项和第项,即第6项和第7项的二项式系数相等,且最大.故选:BC
(2)二项式的展开式中,每项的系数与二项式系数相等,共有12项
所以系数最大的项为第六项和第七项故选:BC
(3)∵的展开式中只有第项的二项式系数最大,∴为偶数,展开式共有项,则.
的展开式的通项公式为,令,得.
∴展开式中含项的系数是,故选D.
【一隅三反】
1.(2020·辽宁沈阳市·高二期中)在的二项展开式中,若只有第5项的二项式系数最大,则的二项展开式中的常数项为( )
A.960 B.1120 C.-560 D.-960
【答案】B
【解析】在(x﹣1)n(n∈N+)的二项展开式中,若只有第5项的二项式系数最大,则n=8,
则=的二项展开式的通项公式为Tr+1= 28﹣r (﹣1)r x4﹣r,
令4﹣r=0,求得r=4,可得展开式中的常数项为 24 (﹣1)4=1120,故选B.
2.(2021·湖南常德市)的展开式中各项系数的和为2,则该展开式中常数项为( )
A. B. C.10 D.20
【答案】C
【解析】由已知,当时,即,所以展开式中常数项为,故选.
3.(多选)(2020·三亚华侨学校高二开学考试)已知的展开式中第5项的二项式系数最大,则n的值可以为( )
A.7 B.8 C.9 D.10
【答案】ABC
【解析】∵已知的展开式中第5项的二项式系数最大,则或n=8或n=9故选:ABC.
4.(2020·全国高二课时练习)已知展开式中各项系数的和为m,且,求展开式中二项式系数最大的项的系数 .
【答案】59136
【解析】设,令,得,
所以,则展开式中有13项,且中间一项(第7项)的二项式系数最大,
该项为.故所求的系数为59136.
5.(2020·重庆市第七中学校高二月考)二项式 的展开式中,二项式系数最大的项是第4项,则其展开式中的常数项是_________.
【答案】-20
【解析】由题意知,展开式中有7项,.因为
令,得,所以常数项为.
考法五 二项式系数或系数和
【例5】(2020·安徽省泗县)若.
求:(1);
(2);
(3).
【答案】(1)27;(2)14;(3)27.
【解析】(1)令,可得,
∴.①
(2)令可得,
∴.②
由①②得,
∴.
(3)由题意得二项式展开式的通项为,
∴每项的系数,
∴.
【一隅三反】
1.(2020·北京朝阳区·高二期末)在的二项展开式中,二项式系数之和为___________;所有项的系数之和为_______.
【答案】
【解析】根据二项展开式的性质,展开式的二项式系数之和为,
令可得所有项的系数之和为,故答案为:,
2.(2020·全国高二单元测试)若(-x)10=a0+a1x+a2x2+…+a10x10,则(a0+a2+…+a10)2-(a1+a3+…+a9)2=
【答案】1
【解析】令,得,令,得,
.故选:A.
3.(2020·福建厦门市·厦门双十中学高二期中)已知 ,则_____.
【答案】
【解析】对等式两边求导,得,令,则.
4.(2020·宁县第二中学高二期中)设展开式中只有第1010项的二项式系数最大.
(1)求n;
(2)求;
(3)求..
【答案】(1)2018;(2);(3)-1.
【解析】(1)由二项式系数的对称性,
(2)
(3)令 ,得,
令,得,故.
考法六 二项式定理运用
【例6】(1)(2020·上海市七宝中学高二期中)除以100的余数是________
(2)(2020·全国高二单元测试)的计算结果精确到0.01的近似值是_________
【答案】(1)41(2)1.34
【解析】(1)
即除以100的余数为.故答案为:.
(2)故答案为:
【一隅三反】
1.(2020·四川棠湖中学高二月考)已知能够被15整除,则________.
【答案】14
【解析】由题可知,
所以,
而75能被15整除,要使能够被15整除,只需能被15整除即可,
所以,解得:.故答案为:14.
2.(2020·江苏泰州市·泰州中学高二期中)被除所得的余数是_____________.
【答案】1
【解析】因为
,
所以转化为求被除所得的余数,
因为,所以被除所得的余数是1,故答案为:1
3.(2021·河北保定市)的计算结果精确到0.001的近似值是
【答案】0.941
【解析】
故选B
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
