23.2解直角三角形及其应用同步练习(含答案)-沪科版数学九年级上册
文档属性
| 名称 | 23.2解直角三角形及其应用同步练习(含答案)-沪科版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 504.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 00:00:00 | ||
图片预览



文档简介
23.2解直角三角形及其应用同步练习-沪科版数学九年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,市规划局准备修建一座高的过街天桥,已知天桥的坡面的坡度,则坡面的长度为( )
A.10m B.8m C.6m D.
2.如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
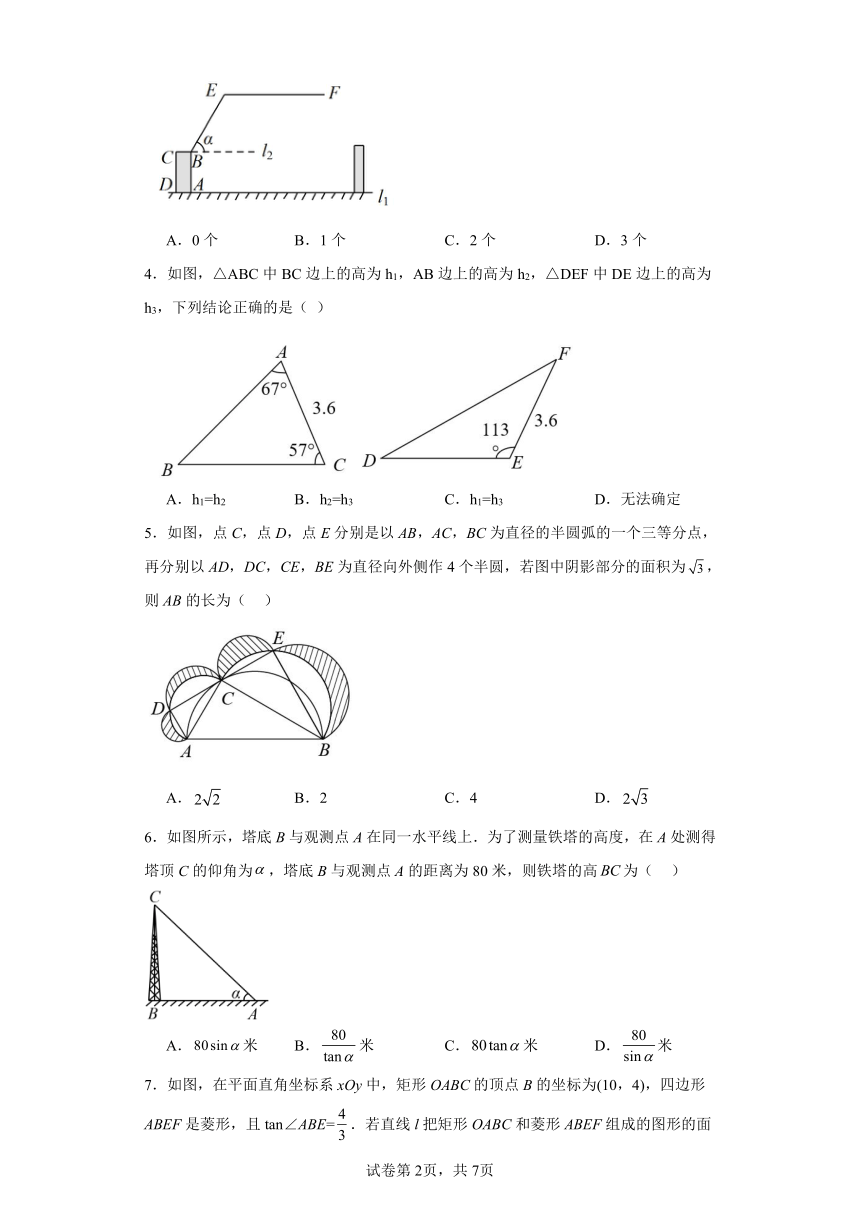
3.某限高曲臂道路闸口如图所示,垂直地面于点,与水平线的夹角为,,若米,米,车辆的高度为(单位:米),不考虑闸口与车辆的宽度.
①当时,小于3.3米的车辆均可以通过该闸口;
②当时,等于2.9米的车辆不可以通过该闸口;
③当时,等于3.1米的车辆不可以通过该闸口.
则上述说法正确的个数为( )
A.0个 B.1个 C.2个 D.3个
4.如图,△ABC中BC边上的高为h1,AB边上的高为h2,△DEF中DE边上的高为h3,下列结论正确的是( )
A.h1=h2 B.h2=h3 C.h1=h3 D.无法确定
5.如图,点C,点D,点E分别是以AB,AC,BC为直径的半圆弧的一个三等分点,再分别以AD,DC,CE,BE为直径向外侧作4个半圆,若图中阴影部分的面积为,则AB的长为( )
A. B.2 C.4 D.
6.如图所示,塔底B与观测点A在同一水平线上.为了测量铁塔的高度,在A处测得塔顶C的仰角为,塔底B与观测点A的距离为80米,则铁塔的高为( )
A.米 B.米 C.米 D.米
7.如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A. B.
C. D.
8.周末,小明和小华来滨湖新区渡江纪念馆游玩,看到高雄挺拔的“胜利之塔”,萌发了用所学知识测量塔高的想法,如图,他俩在塔前的平地上选择一点,树立测角仪,测出看塔顶的仰角约为,从点向塔底走米到达点,测出看塔顶的仰角约为,已知测角仪器高为米,则塔的高大约为( )
A.141米 B.101米 C.91米 D.96米
9.我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在 A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( ).(参考数据sin53°≈0.80,cos53°≈0.60)
A.12千米 B.(3+4)千米 C.(3+5)千米 D.(12﹣4)千米
10.如图,中,,,是的中点,点在上,,则的值为( )
A. B. C. D.
二、填空题
11.在中,,则
12.一数学兴趣小组来到某公园,测量一座塔的高度.如图,在 A 处测得塔顶的仰角为α=31°,在 B 处测得塔顶的仰角为β=45°,又测量出 A、B 两点的距离为20米,则塔高为 米.(参考数值:tan31°≈)
13.已知一斜坡的坡比为1:2,坡角为,那么 .
14.如图,正方形中,,AB与直线l所夹锐角为60°,延长交直线l于点,作正方形,延长交直线l于点,作正方形,延长交直线l于点,作正方形…,依此规律,则线段 ,线段 .
15.如图,在矩形中,,,E为边的中点,连接,,点F,G分别是,边上的两个动点,连接,将沿折叠,使点B的对应点H恰好落在边上,若是以为腰的等腰三角形,则的长为 .
16.如图,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.请你根据图中数据计算回答,请你根据图中数据计算回答:小敏身高米,她乘电梯会有碰头危险吗? .(填是或否)(可能用到的参考数值:,,)
17.如图,渔船在处看到灯塔在北偏东方向上,渔船向正东方向航行了到达处,在处看到灯塔在正北方向上,则处与灯塔的距离是 .
18.如图,在矩形ABCD中,AB=10,点E是AD边上的一点,将ABE沿着BE折叠,点A刚好落在CD边上点G处,点F为CG上的一点,将BCF沿着BF折叠,点C恰好落在BG上点H处,若=3:5,连接AG,则点H到AG的距离为 .
19.如图,为了求出湖两岸、两点之间的距离,观测者在湖边找到一点,并分别测,,又量得,则、两点之间距离为 (结果保留根号).
20.为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为,若亮亮身高1.70米,则无人机距离地面的高度约为 米.(结果精确到0.1米,参考数据:,)
三、解答题
21.建筑物MN一侧有一斜坡AC,在斜坡坡脚A处测得建筑物顶部N的仰角为60°,当太阳光线与水平线夹角成45°时,建筑物MN的影子的一部分在水平地面上MA处,另一部分影子落在斜坡上AP处,已知点P的距水平地面AB的高度米,斜坡AC的坡度为(即),且M,A,D,B在同一条直线上.(测倾器的高度忽略不计,结果保留根号)
(1)求此时建筑物MN落在斜坡上的影子AP的长;
(2)求建筑物MN的高度.
22.如图所示,在Rt△ABC中,a,b分别是∠A,∠B的对边,c为斜边,如果已知两个元素a,∠B,就可以求出其余三个未知元素b,c,∠A.
(1)求解的方法有多种,请你按照下列步骤,完成一种求解过程.
第一步:已知:a,∠B,用关系式:_______________,求出:________________;
第二步:已知:_____,用关系式:_______________,求出:_________________;
第三步:已知:_____,用关系式:_______________,求出:_________________.
(2)请你分别给出a,∠B的一个具体数据,然后按照(1)中的思路,求出b,c,∠A的值.
23.等腰三角形ABC的腰长AB=AC=5,底边BC=6,求.
24.城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14 m的D处有一大坝,背水坡CD的坡度i=1∶2,坝高CF为2 m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2 m的人行道.
(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域,≈1.732,≈1.414)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.C
3.C
4.B
5.A
6.C
7.D
8.D
9.B
10.C
11.
12.30
13.
14. /
15.或
16.否
17.
18..
19.
20.10.4
21.(1)米;
(2)米.
22.(1) ∠A ;atanB ;;(2)答案不唯一.
23.
24.(1)BF=18m;(2)故需封闭人行道DE.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,市规划局准备修建一座高的过街天桥,已知天桥的坡面的坡度,则坡面的长度为( )
A.10m B.8m C.6m D.
2.如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
3.某限高曲臂道路闸口如图所示,垂直地面于点,与水平线的夹角为,,若米,米,车辆的高度为(单位:米),不考虑闸口与车辆的宽度.
①当时,小于3.3米的车辆均可以通过该闸口;
②当时,等于2.9米的车辆不可以通过该闸口;
③当时,等于3.1米的车辆不可以通过该闸口.
则上述说法正确的个数为( )
A.0个 B.1个 C.2个 D.3个
4.如图,△ABC中BC边上的高为h1,AB边上的高为h2,△DEF中DE边上的高为h3,下列结论正确的是( )
A.h1=h2 B.h2=h3 C.h1=h3 D.无法确定
5.如图,点C,点D,点E分别是以AB,AC,BC为直径的半圆弧的一个三等分点,再分别以AD,DC,CE,BE为直径向外侧作4个半圆,若图中阴影部分的面积为,则AB的长为( )
A. B.2 C.4 D.
6.如图所示,塔底B与观测点A在同一水平线上.为了测量铁塔的高度,在A处测得塔顶C的仰角为,塔底B与观测点A的距离为80米,则铁塔的高为( )
A.米 B.米 C.米 D.米
7.如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A. B.
C. D.
8.周末,小明和小华来滨湖新区渡江纪念馆游玩,看到高雄挺拔的“胜利之塔”,萌发了用所学知识测量塔高的想法,如图,他俩在塔前的平地上选择一点,树立测角仪,测出看塔顶的仰角约为,从点向塔底走米到达点,测出看塔顶的仰角约为,已知测角仪器高为米,则塔的高大约为( )
A.141米 B.101米 C.91米 D.96米
9.我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在 A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( ).(参考数据sin53°≈0.80,cos53°≈0.60)
A.12千米 B.(3+4)千米 C.(3+5)千米 D.(12﹣4)千米
10.如图,中,,,是的中点,点在上,,则的值为( )
A. B. C. D.
二、填空题
11.在中,,则
12.一数学兴趣小组来到某公园,测量一座塔的高度.如图,在 A 处测得塔顶的仰角为α=31°,在 B 处测得塔顶的仰角为β=45°,又测量出 A、B 两点的距离为20米,则塔高为 米.(参考数值:tan31°≈)
13.已知一斜坡的坡比为1:2,坡角为,那么 .
14.如图,正方形中,,AB与直线l所夹锐角为60°,延长交直线l于点,作正方形,延长交直线l于点,作正方形,延长交直线l于点,作正方形…,依此规律,则线段 ,线段 .
15.如图,在矩形中,,,E为边的中点,连接,,点F,G分别是,边上的两个动点,连接,将沿折叠,使点B的对应点H恰好落在边上,若是以为腰的等腰三角形,则的长为 .
16.如图,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.请你根据图中数据计算回答,请你根据图中数据计算回答:小敏身高米,她乘电梯会有碰头危险吗? .(填是或否)(可能用到的参考数值:,,)
17.如图,渔船在处看到灯塔在北偏东方向上,渔船向正东方向航行了到达处,在处看到灯塔在正北方向上,则处与灯塔的距离是 .
18.如图,在矩形ABCD中,AB=10,点E是AD边上的一点,将ABE沿着BE折叠,点A刚好落在CD边上点G处,点F为CG上的一点,将BCF沿着BF折叠,点C恰好落在BG上点H处,若=3:5,连接AG,则点H到AG的距离为 .
19.如图,为了求出湖两岸、两点之间的距离,观测者在湖边找到一点,并分别测,,又量得,则、两点之间距离为 (结果保留根号).
20.为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为,若亮亮身高1.70米,则无人机距离地面的高度约为 米.(结果精确到0.1米,参考数据:,)
三、解答题
21.建筑物MN一侧有一斜坡AC,在斜坡坡脚A处测得建筑物顶部N的仰角为60°,当太阳光线与水平线夹角成45°时,建筑物MN的影子的一部分在水平地面上MA处,另一部分影子落在斜坡上AP处,已知点P的距水平地面AB的高度米,斜坡AC的坡度为(即),且M,A,D,B在同一条直线上.(测倾器的高度忽略不计,结果保留根号)
(1)求此时建筑物MN落在斜坡上的影子AP的长;
(2)求建筑物MN的高度.
22.如图所示,在Rt△ABC中,a,b分别是∠A,∠B的对边,c为斜边,如果已知两个元素a,∠B,就可以求出其余三个未知元素b,c,∠A.
(1)求解的方法有多种,请你按照下列步骤,完成一种求解过程.
第一步:已知:a,∠B,用关系式:_______________,求出:________________;
第二步:已知:_____,用关系式:_______________,求出:_________________;
第三步:已知:_____,用关系式:_______________,求出:_________________.
(2)请你分别给出a,∠B的一个具体数据,然后按照(1)中的思路,求出b,c,∠A的值.
23.等腰三角形ABC的腰长AB=AC=5,底边BC=6,求.
24.城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14 m的D处有一大坝,背水坡CD的坡度i=1∶2,坝高CF为2 m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2 m的人行道.
(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域,≈1.732,≈1.414)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.C
3.C
4.B
5.A
6.C
7.D
8.D
9.B
10.C
11.
12.30
13.
14. /
15.或
16.否
17.
18..
19.
20.10.4
21.(1)米;
(2)米.
22.(1) ∠A ;atanB ;;(2)答案不唯一.
23.
24.(1)BF=18m;(2)故需封闭人行道DE.
答案第1页,共2页
答案第1页,共2页
