22.5综合于实践测量与误差同步练习-沪科版数学九年级上册(含答案)
文档属性
| 名称 | 22.5综合于实践测量与误差同步练习-沪科版数学九年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 436.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 22:19:08 | ||
图片预览


文档简介
22.5综合于实践测量与误差同步练习-沪科版数学九年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某校兴趣小组为了测量教学大楼的高度,用1.5m的竹竿作为测量工具.在阳光明媚的某天,该兴趣小组移动竹竿,使得竹竿顶端的影子与楼顶的影子在地面处重合,如图,测得,,则教学楼的高是( )
A. B. C. D.
2.太阳光照射下的某一时刻,高的竹竿影长,那么影长为的旗杆的高是( )
A. B. C. D.
3.在某一时刻,测得一根高为的竹杆的影长为,同时测得一栋楼的影长为,则这栋楼的高度为( )
A. B. C. D.
4.一个钢筋三角架三边长分别为,,,现在要做一个和它相似的钢筋三角架,而只有长为和的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
A.一种 B.两种 C.三种 D.四种或四种以上
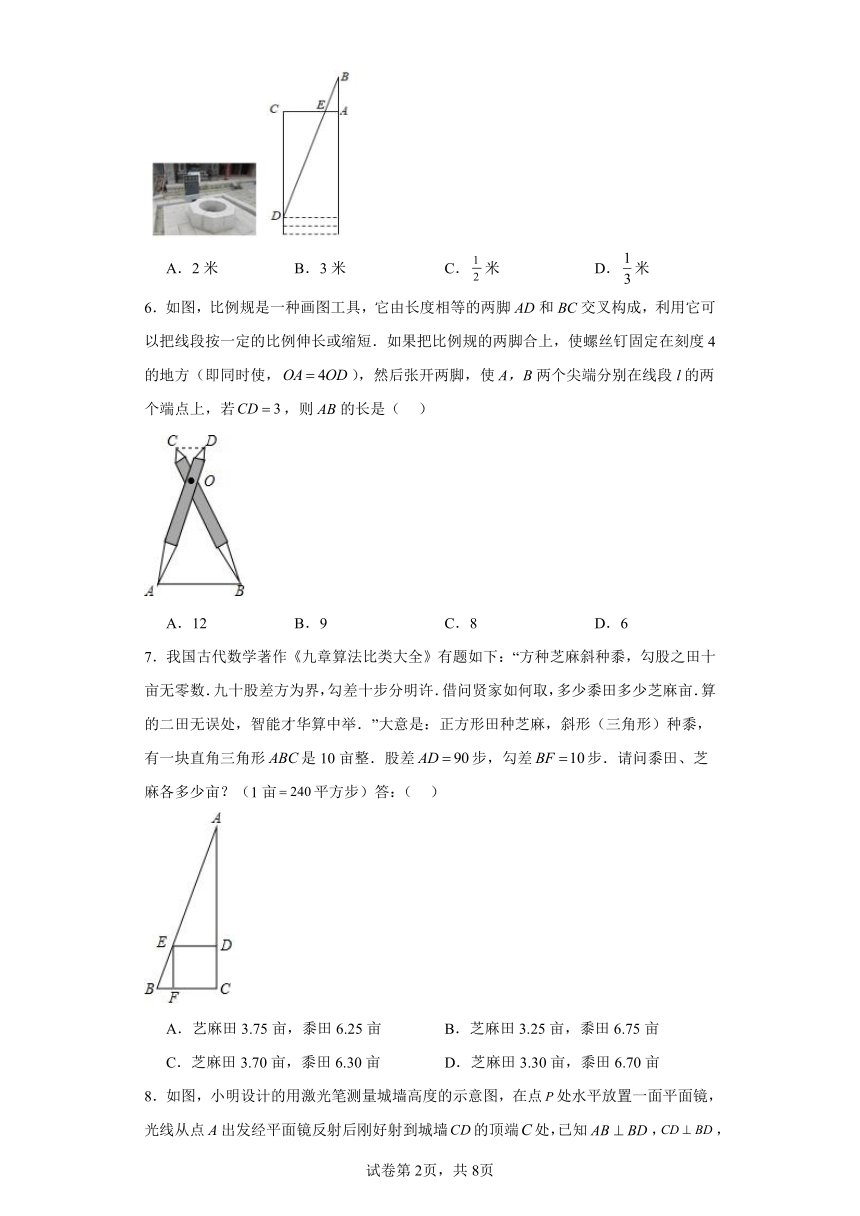
5.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口处立一根垂直于井口的木杆,从木杆的顶端处观察井水水岸处,视线与井口的直径交于点,如果测得米,米,米,那么的长为( )
A.2米 B.3米 C.米 D.米
6.如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使,),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若,则AB的长是( )
A.12 B.9 C.8 D.6
7.我国古代数学著作《九章算法比类大全》有题如下:“方种芝麻斜种黍,勾股之田十亩无零数.九十股差方为界,勾差十步分明许.借问贤家如何取,多少黍田多少芝麻亩.算的二田无误处,智能才华算中举.”大意是:正方形田种芝麻,斜形(三角形)种黍,有一块直角三角形是10亩整.股差步,勾差步.请问黍田、芝麻各多少亩?(1亩平方步)答:( )
A.艺麻田3.75亩,黍田6.25亩 B.芝麻田3.25亩,黍田6.75亩
C.芝麻田3.70亩,黍田6.30亩 D.芝麻田3.30亩,黍田6.70亩
8.如图,小明设计的用激光笔测量城墙高度的示意图,在点处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙的顶端处,已知,,米,米,米,那么该城墙的高度为( )
A.6 B.8 C.10 D.18
9.在一次测量活动中,为了测量河两岸A地与B地之间的距离,某研究性学习小组建立了如图所示的数学模型,,测得,则A地与B地之间的距离为( )
A.80 B.50 C.100 D.100
10.在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
A.6.93米 B.8米 C.11.8米 D.12米
二、填空题
11.在某一时刻,测得身高为的小明的影长为,同时测得一幢高楼的影长为,则这幢高楼的高度为 .
12.如图,为了估算河的宽度,在河对岸选定一个目标作为点,再在河的这一边选点和,使,然后,再选点,使,用视线确定和的交点.此时如果测得米,米,米,则两岸间的大致距离为 米.
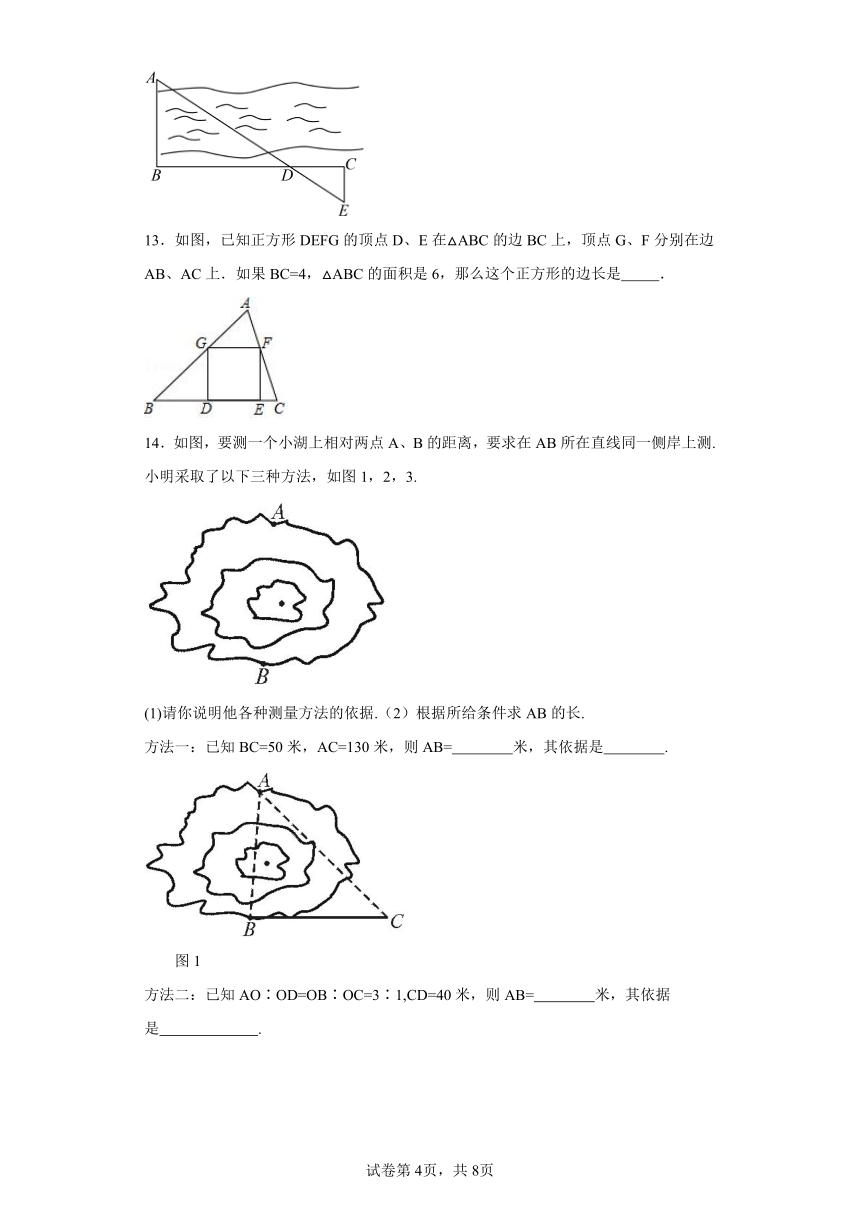
13.如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是 .
14.如图,要测一个小湖上相对两点A、B的距离,要求在AB所在直线同一侧岸上测.小明采取了以下三种方法,如图1,2,3.
(1)请你说明他各种测量方法的依据.(2)根据所给条件求AB的长.
方法一:已知BC=50米,AC=130米,则AB= 米,其依据是 .
图1
方法二:已知AO∶OD=OB∶OC=3∶1,CD=40米,则AB= 米,其依据是 .
图2
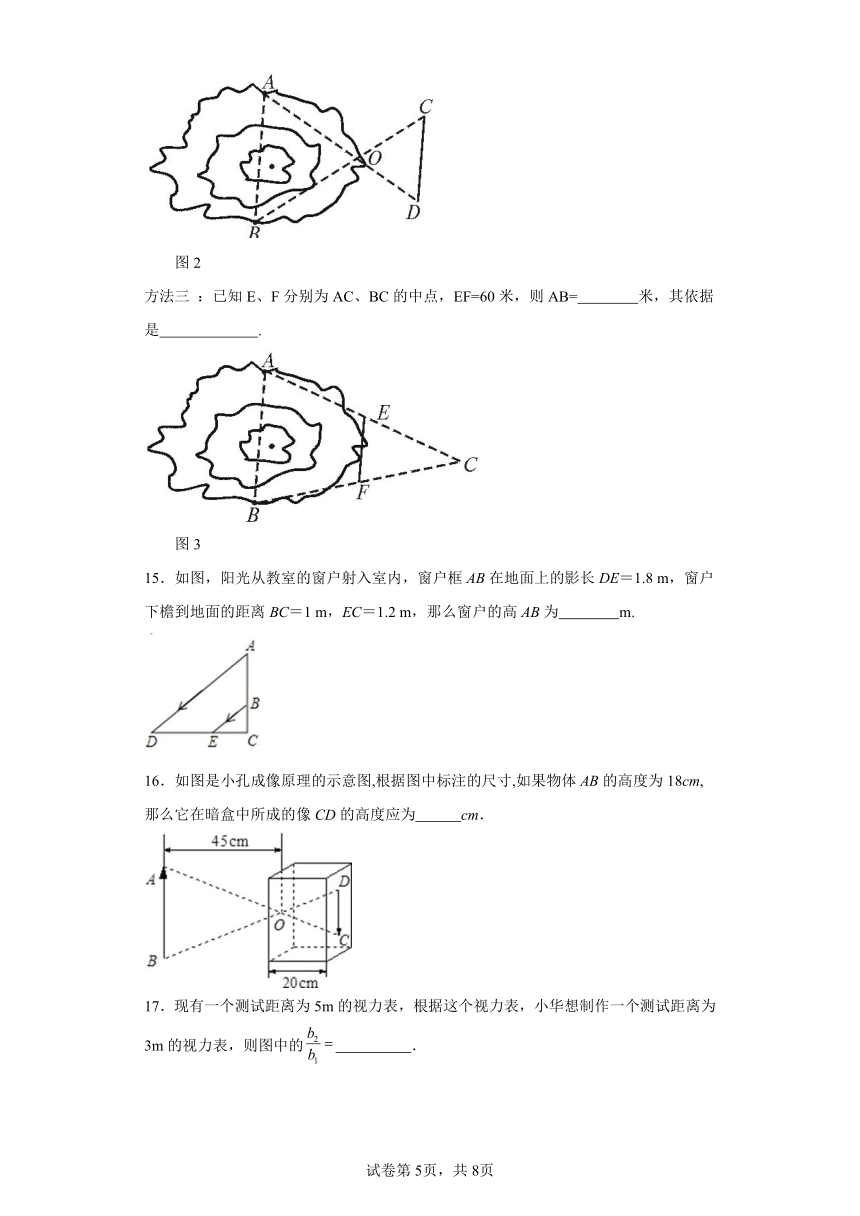
方法三 :已知E、F分别为AC、BC的中点,EF=60米,则AB= 米,其依据是 .
图3
15.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,EC=1.2 m,那么窗户的高AB为 m.
16.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为18cm,那么它在暗盒中所成的像CD的高度应为 cm.
17.现有一个测试距离为5m的视力表,根据这个视力表,小华想制作一个测试距离为3m的视力表,则图中的 .
18.如图,已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外,将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为 米.
19.小明身高1.76米,小亮身高1.6米,同一时刻他们站在太阳光下,小明的影子长为1米,则小亮的影长是 米.
20.如图,是斜靠在墙上的长梯,梯脚B距离墙角,梯上点D距墙,长,则梯子长为 m.
三、解答题
21.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯的高度.如图,当李明走到点处时,张龙测得李明直立时身高与影子长正好相等;接着李明沿方向继续向前走,走到点处时,李明直立时身高的影子恰好是线段,并测得,已知李明直立时的身高为,求路灯的高的长.(结果精确到.
22.同一时刻两根木杆在太阳光下的影子如图所示,木杆AB长为3m,其影子BC长1.6m,木杆QP长为4.8m,它的部分影子PM长为2m,还有一部分落到墙上的MN处,求墙上影子MN的长度.
23.如意塔,也称火炬塔,是咸阳地标性建筑,位于成阳市秦都区双照镇北塬大道奥体中心东侧的双照湖,建筑形态典雅端庄,落落大方,与体育场形成“天圆地方”的文化寓意.数学实践小组为了测量该塔的高度(塔的底部可以到达,顶部不能到达),准备了如下测量工具:①镜子;②皮尺;③长为2米的标杆;④高为1.5米的测角仪(能测量仰角和俯角的仪器),请你用所学的知识,帮助他们设计测量方案,回答下列问题
(1)在你设计的方案中,选用的测量工具是______;(填具的序号)
(2)在图中画出你的测量方案示意图,你需要测得示意图中的哪些数据(用a、b、c等表示测得线段的长度,用、等表示测得角的度数,无需写出测量过程),并用所测数据表示出该塔的高.
24.如图,小明晚上从路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的顶部.已知小明的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少?
25.新型冠状病毒感染引发“疫情就是命令,现场就是战场”家住武汉火神山医院旁的小华,目睹这与时间赛跑的建设场面,在家里的小华从离窗台A水平距离2m的M点望去,通过窗台A处刚好俯瞰到远处医院箱式板房顶部远端E点,小华又向窗户方向前进0.8m到Q点,恰好通过窗台A处看到板房顶部近处D点,已知AB、CD、EF、MN都垂直于地面BC,N、F在直线BC上,MQ、DE都平行于地面BC,BC长300m,请你帮助小华计算DE的长度.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.B
3.A
4.B
5.B
6.A
7.A
8.B
9.C
10.B
11.
12.100
13.
14. 120 △ABC为直角三角形,根据勾股定理可得AB长. 120 △AOB∽△DOC则对应边成比例. 120 EF是△ABC的中位线,由三角形中位线定理得EF=AB.
15.1.5
16.8
17.
18.7.5
19.
20.
21.路灯的高CD的长约为6.1m
22.1.05m
23.(1)②③
(2)米
24.30m.
25.500
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某校兴趣小组为了测量教学大楼的高度,用1.5m的竹竿作为测量工具.在阳光明媚的某天,该兴趣小组移动竹竿,使得竹竿顶端的影子与楼顶的影子在地面处重合,如图,测得,,则教学楼的高是( )
A. B. C. D.
2.太阳光照射下的某一时刻,高的竹竿影长,那么影长为的旗杆的高是( )
A. B. C. D.
3.在某一时刻,测得一根高为的竹杆的影长为,同时测得一栋楼的影长为,则这栋楼的高度为( )
A. B. C. D.
4.一个钢筋三角架三边长分别为,,,现在要做一个和它相似的钢筋三角架,而只有长为和的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
A.一种 B.两种 C.三种 D.四种或四种以上
5.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口处立一根垂直于井口的木杆,从木杆的顶端处观察井水水岸处,视线与井口的直径交于点,如果测得米,米,米,那么的长为( )
A.2米 B.3米 C.米 D.米
6.如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使,),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若,则AB的长是( )
A.12 B.9 C.8 D.6
7.我国古代数学著作《九章算法比类大全》有题如下:“方种芝麻斜种黍,勾股之田十亩无零数.九十股差方为界,勾差十步分明许.借问贤家如何取,多少黍田多少芝麻亩.算的二田无误处,智能才华算中举.”大意是:正方形田种芝麻,斜形(三角形)种黍,有一块直角三角形是10亩整.股差步,勾差步.请问黍田、芝麻各多少亩?(1亩平方步)答:( )
A.艺麻田3.75亩,黍田6.25亩 B.芝麻田3.25亩,黍田6.75亩
C.芝麻田3.70亩,黍田6.30亩 D.芝麻田3.30亩,黍田6.70亩
8.如图,小明设计的用激光笔测量城墙高度的示意图,在点处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙的顶端处,已知,,米,米,米,那么该城墙的高度为( )
A.6 B.8 C.10 D.18
9.在一次测量活动中,为了测量河两岸A地与B地之间的距离,某研究性学习小组建立了如图所示的数学模型,,测得,则A地与B地之间的距离为( )
A.80 B.50 C.100 D.100
10.在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
A.6.93米 B.8米 C.11.8米 D.12米
二、填空题
11.在某一时刻,测得身高为的小明的影长为,同时测得一幢高楼的影长为,则这幢高楼的高度为 .
12.如图,为了估算河的宽度,在河对岸选定一个目标作为点,再在河的这一边选点和,使,然后,再选点,使,用视线确定和的交点.此时如果测得米,米,米,则两岸间的大致距离为 米.
13.如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是 .
14.如图,要测一个小湖上相对两点A、B的距离,要求在AB所在直线同一侧岸上测.小明采取了以下三种方法,如图1,2,3.
(1)请你说明他各种测量方法的依据.(2)根据所给条件求AB的长.
方法一:已知BC=50米,AC=130米,则AB= 米,其依据是 .
图1
方法二:已知AO∶OD=OB∶OC=3∶1,CD=40米,则AB= 米,其依据是 .
图2
方法三 :已知E、F分别为AC、BC的中点,EF=60米,则AB= 米,其依据是 .
图3
15.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8 m,窗户下檐到地面的距离BC=1 m,EC=1.2 m,那么窗户的高AB为 m.
16.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为18cm,那么它在暗盒中所成的像CD的高度应为 cm.
17.现有一个测试距离为5m的视力表,根据这个视力表,小华想制作一个测试距离为3m的视力表,则图中的 .
18.如图,已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外,将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为 米.
19.小明身高1.76米,小亮身高1.6米,同一时刻他们站在太阳光下,小明的影子长为1米,则小亮的影长是 米.
20.如图,是斜靠在墙上的长梯,梯脚B距离墙角,梯上点D距墙,长,则梯子长为 m.
三、解答题
21.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯的高度.如图,当李明走到点处时,张龙测得李明直立时身高与影子长正好相等;接着李明沿方向继续向前走,走到点处时,李明直立时身高的影子恰好是线段,并测得,已知李明直立时的身高为,求路灯的高的长.(结果精确到.
22.同一时刻两根木杆在太阳光下的影子如图所示,木杆AB长为3m,其影子BC长1.6m,木杆QP长为4.8m,它的部分影子PM长为2m,还有一部分落到墙上的MN处,求墙上影子MN的长度.
23.如意塔,也称火炬塔,是咸阳地标性建筑,位于成阳市秦都区双照镇北塬大道奥体中心东侧的双照湖,建筑形态典雅端庄,落落大方,与体育场形成“天圆地方”的文化寓意.数学实践小组为了测量该塔的高度(塔的底部可以到达,顶部不能到达),准备了如下测量工具:①镜子;②皮尺;③长为2米的标杆;④高为1.5米的测角仪(能测量仰角和俯角的仪器),请你用所学的知识,帮助他们设计测量方案,回答下列问题
(1)在你设计的方案中,选用的测量工具是______;(填具的序号)
(2)在图中画出你的测量方案示意图,你需要测得示意图中的哪些数据(用a、b、c等表示测得线段的长度,用、等表示测得角的度数,无需写出测量过程),并用所测数据表示出该塔的高.
24.如图,小明晚上从路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的顶部.已知小明的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少?
25.新型冠状病毒感染引发“疫情就是命令,现场就是战场”家住武汉火神山医院旁的小华,目睹这与时间赛跑的建设场面,在家里的小华从离窗台A水平距离2m的M点望去,通过窗台A处刚好俯瞰到远处医院箱式板房顶部远端E点,小华又向窗户方向前进0.8m到Q点,恰好通过窗台A处看到板房顶部近处D点,已知AB、CD、EF、MN都垂直于地面BC,N、F在直线BC上,MQ、DE都平行于地面BC,BC长300m,请你帮助小华计算DE的长度.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.B
3.A
4.B
5.B
6.A
7.A
8.B
9.C
10.B
11.
12.100
13.
14. 120 △ABC为直角三角形,根据勾股定理可得AB长. 120 △AOB∽△DOC则对应边成比例. 120 EF是△ABC的中位线,由三角形中位线定理得EF=AB.
15.1.5
16.8
17.
18.7.5
19.
20.
21.路灯的高CD的长约为6.1m
22.1.05m
23.(1)②③
(2)米
24.30m.
25.500
答案第1页,共2页
答案第1页,共2页
