24.2圆的基本性质同步练习-(含答案)沪科版数学九年级下册
文档属性
| 名称 | 24.2圆的基本性质同步练习-(含答案)沪科版数学九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 592.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 00:00:00 | ||
图片预览


文档简介
24.2圆的基本性质同步练习-沪科版数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,一个直角三角形ABC的斜边AB与量角器的零刻度线重合,点D对应56°,则∠BCD的度数为( )
A. B. C. D.
2.半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是
A.3 B.4 C. D.
3.如图,一个底部呈球形的烧瓶,球的半径为,瓶内液体的最大深度,则截面圆中弦的长为( )cm.
A. B.6 C.8 D.8.4
4.如图,为的直径,,为上的两点,且为的中点,若,则的度数为( )
A. B. C. D.
5.已知∠A=Rt∠,AB=4,AE=2,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则的最大值为( )
A. B. C. D.
6.如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )
A.70° B.80° C.90° D.100°
7.已知,点A为⊙O所在平面上一点,且点A到⊙O上所有点的距离中,最长为5,最短为1,则⊙O的半径为( )
A.2 B.2.5 C.3 D.2或3
8.如图,AB为⊙O的直径,CD为⊙O的弦,CD⊥AB,垂足为E,OE=3,CD=8,AB=( )
A. B.10 C. D.5
9.边长为的正三角形的外接圆的半径为
A. B. C. D.
10.如图,平面直角坐标系中,点A是y轴正半轴上任意一点,B(-3,0),C(4,0),则当点A在y轴上运动时,△ABC的外心不可能在( )
A.第三象限 B.第一象限 C.第四象限 D.x轴上
二、填空题
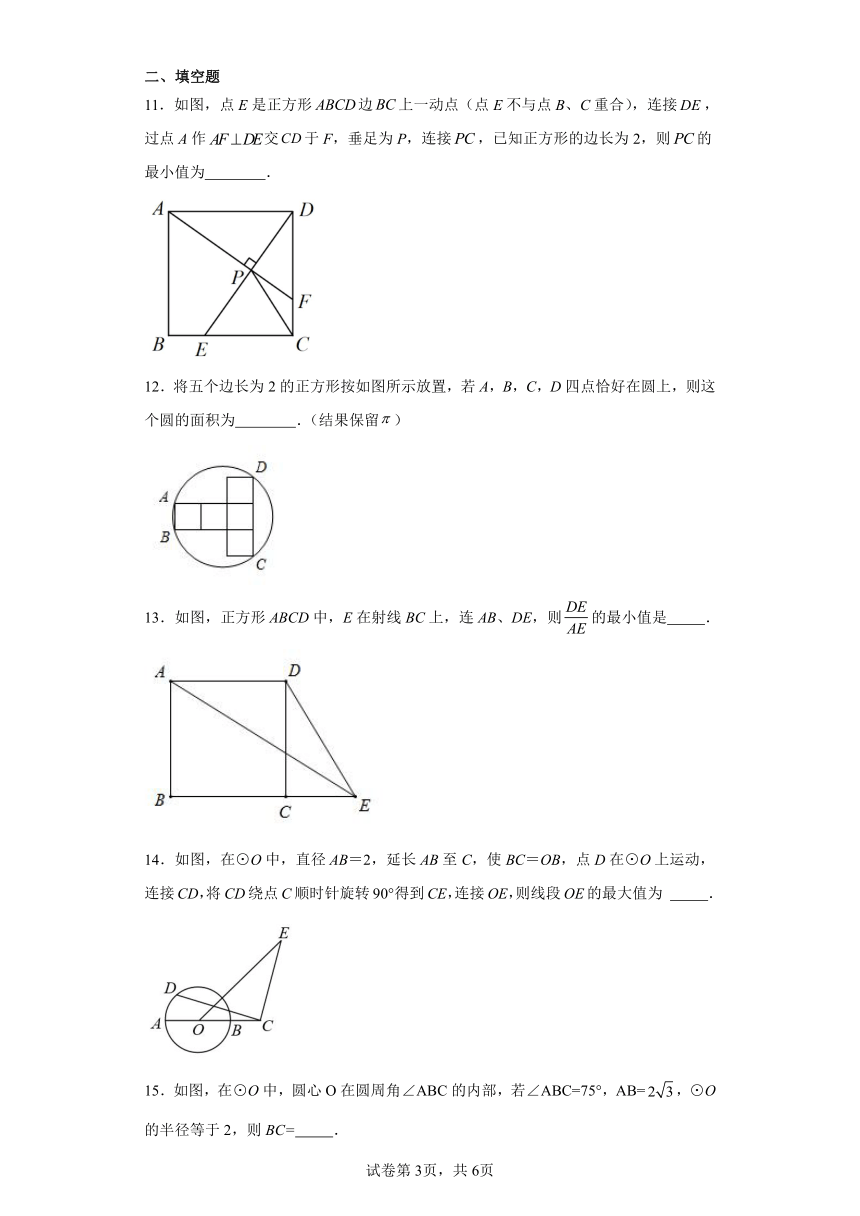
11.如图,点E是正方形边上一动点(点E不与点B、C重合),连接,过点A作交于F,垂足为P,连接,已知正方形的边长为2,则的最小值为 .
12.将五个边长为2的正方形按如图所示放置,若A,B,C,D四点恰好在圆上,则这个圆的面积为 .(结果保留)
13.如图,正方形ABCD中,E在射线BC上,连AB、DE,则的最小值是 .
14.如图,在⊙O中,直径AB=2,延长AB至C,使BC=OB,点D在⊙O上运动,连接CD,将CD绕点C顺时针旋转90°得到CE,连接OE,则线段OE的最大值为 .
15.如图,在⊙O中,圆心O在圆周角∠ABC的内部,若∠ABC=75°,AB=,⊙O的半径等于2,则BC= .
16.图1是郑州的网红打卡点 “戒指桥”, 其数学模型如图2所示. 线段是其中一条拉索, 点在圆上, 点是圆和水平桥面的交点. 小明测得, 且在 B点和点观测点的仰角均为, 则点到桥面的距离为 , “戒指” 的半径为 .
17.如图,某古城大门口的平面图上方是半圆,下方是矩形,有一辆装货后宽3米的货车从大门中间进入古城,那么货车装货后的最大高度为 米.
18.如图,AB为⊙O的弦,C为弦AB上一点,设AC=m,BC=n(m>n),将弦AB绕圆心O旋转一周,若线段BC扫过的面积为(m2﹣n2)π,则=
19.如图,的半径为,,则弦的长为 .
20.如图,在半径为5的⊙O中,弦AB=6,OC⊥AB于点D,交⊙O于点C,则CD= .
三、解答题
21.在中,,,,以点为圆心,以长为半径作圆,试判断点和点与的位置关系.
22.2022年月日,合肥古逍遥津公园摩天轮“庐州之眼”正式开放,对外营业.该摩天轮静止时最高点到地面的距离为米,最低点到地面的距离为米,点是摩天轮的圆心,是其垂直于地面的直径,若摩天轮匀速运行一周需要分钟,某人在摩天轮启动前在点处,摩天轮开启后匀速运行秒后,求某人距离地面的高度.(结果精确到米,参考数据:,,,,,.)
23.如图1,P是正方形边上一点,线段与关于直线对称,连接并延长交直线于点F,连接.
(1)补全图形,求的大小;
(2)用等式表示线段之间的数量关系,并证明;
(3)连接,G是的中点,,若点P从点B运动到点C,直接写出的最大值.
24.如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点,点O为坐标原点.
(1)该图中弧所在圆的圆心D的坐标为 ;
(2)根据(1)中的条件填空:
①圆D的半径= (结果保留根号);
②点(7,0)在圆D (填“上”、“内”或“外”);
③∠ADC的度数为 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.C
3.C
4.C
5.C
6.C
7.D
8.B
9.C
10.A
11.
12.
13.
14./
15.
16. 14 26
17.5
18.
19.4
20.
21.点在圆外.
22.米.
23.(1)
(2),
(3)
24.(1)(2,0); (2)①; ②外; ③90°;
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,一个直角三角形ABC的斜边AB与量角器的零刻度线重合,点D对应56°,则∠BCD的度数为( )
A. B. C. D.
2.半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是
A.3 B.4 C. D.
3.如图,一个底部呈球形的烧瓶,球的半径为,瓶内液体的最大深度,则截面圆中弦的长为( )cm.
A. B.6 C.8 D.8.4
4.如图,为的直径,,为上的两点,且为的中点,若,则的度数为( )
A. B. C. D.
5.已知∠A=Rt∠,AB=4,AE=2,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则的最大值为( )
A. B. C. D.
6.如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )
A.70° B.80° C.90° D.100°
7.已知,点A为⊙O所在平面上一点,且点A到⊙O上所有点的距离中,最长为5,最短为1,则⊙O的半径为( )
A.2 B.2.5 C.3 D.2或3
8.如图,AB为⊙O的直径,CD为⊙O的弦,CD⊥AB,垂足为E,OE=3,CD=8,AB=( )
A. B.10 C. D.5
9.边长为的正三角形的外接圆的半径为
A. B. C. D.
10.如图,平面直角坐标系中,点A是y轴正半轴上任意一点,B(-3,0),C(4,0),则当点A在y轴上运动时,△ABC的外心不可能在( )
A.第三象限 B.第一象限 C.第四象限 D.x轴上
二、填空题
11.如图,点E是正方形边上一动点(点E不与点B、C重合),连接,过点A作交于F,垂足为P,连接,已知正方形的边长为2,则的最小值为 .
12.将五个边长为2的正方形按如图所示放置,若A,B,C,D四点恰好在圆上,则这个圆的面积为 .(结果保留)
13.如图,正方形ABCD中,E在射线BC上,连AB、DE,则的最小值是 .
14.如图,在⊙O中,直径AB=2,延长AB至C,使BC=OB,点D在⊙O上运动,连接CD,将CD绕点C顺时针旋转90°得到CE,连接OE,则线段OE的最大值为 .
15.如图,在⊙O中,圆心O在圆周角∠ABC的内部,若∠ABC=75°,AB=,⊙O的半径等于2,则BC= .
16.图1是郑州的网红打卡点 “戒指桥”, 其数学模型如图2所示. 线段是其中一条拉索, 点在圆上, 点是圆和水平桥面的交点. 小明测得, 且在 B点和点观测点的仰角均为, 则点到桥面的距离为 , “戒指” 的半径为 .
17.如图,某古城大门口的平面图上方是半圆,下方是矩形,有一辆装货后宽3米的货车从大门中间进入古城,那么货车装货后的最大高度为 米.
18.如图,AB为⊙O的弦,C为弦AB上一点,设AC=m,BC=n(m>n),将弦AB绕圆心O旋转一周,若线段BC扫过的面积为(m2﹣n2)π,则=
19.如图,的半径为,,则弦的长为 .
20.如图,在半径为5的⊙O中,弦AB=6,OC⊥AB于点D,交⊙O于点C,则CD= .
三、解答题
21.在中,,,,以点为圆心,以长为半径作圆,试判断点和点与的位置关系.
22.2022年月日,合肥古逍遥津公园摩天轮“庐州之眼”正式开放,对外营业.该摩天轮静止时最高点到地面的距离为米,最低点到地面的距离为米,点是摩天轮的圆心,是其垂直于地面的直径,若摩天轮匀速运行一周需要分钟,某人在摩天轮启动前在点处,摩天轮开启后匀速运行秒后,求某人距离地面的高度.(结果精确到米,参考数据:,,,,,.)
23.如图1,P是正方形边上一点,线段与关于直线对称,连接并延长交直线于点F,连接.
(1)补全图形,求的大小;
(2)用等式表示线段之间的数量关系,并证明;
(3)连接,G是的中点,,若点P从点B运动到点C,直接写出的最大值.
24.如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点,点O为坐标原点.
(1)该图中弧所在圆的圆心D的坐标为 ;
(2)根据(1)中的条件填空:
①圆D的半径= (结果保留根号);
②点(7,0)在圆D (填“上”、“内”或“外”);
③∠ADC的度数为 .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.C
3.C
4.C
5.C
6.C
7.D
8.B
9.C
10.A
11.
12.
13.
14./
15.
16. 14 26
17.5
18.
19.4
20.
21.点在圆外.
22.米.
23.(1)
(2),
(3)
24.(1)(2,0); (2)①; ②外; ③90°;
答案第1页,共2页
答案第1页,共2页
