第4章几何图形初步 单元综合达标测试题(含答案) 2023—2024学年人教版七年级数学上册
文档属性
| 名称 | 第4章几何图形初步 单元综合达标测试题(含答案) 2023—2024学年人教版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 398.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 21:42:26 | ||
图片预览




文档简介
2023-2024学年人教版七年级数学上册《第4章几何图形初步》
单元综合达标测试题(附答案)
一、单选题(满分32分)
1.下列图形中是正方体表面展开图的是( )
A. B.
C. D.
2.如图,锯木板前,在木板两端固定两个点,用墨盒弹一根墨线然后再锯,这样做的数学道理是( )
A.两点之间线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
3.如图是由个完全相同的小正方体组成的几何体,其从上面看的形状图是( )
A. B. C. D.
4.用一个平面去截下列几何体,截得的平面图形不可能是三角形的是( )
A. B. C. D.
5.如图,共有射线( )
A.4条 B.8条 C.16条 D.32条
6.已知点A、B、C位于直线l上,其中线段,且,若点M是线段的中点,则线段的长为( )
A.1 B.3 C.5或1 D.1或4
7.一人在小岛O点处观察到轮船A在他北偏东的方向上,轮船B在他南偏东的方向上,那么此时的度数为( )
A. B. C. D.
8.如图,是的平分线,是的平分线,且,则为( )
A. B. C. D.
二、填空题(满分32分)
9.把化成用度表示的角是 .
10.如图,小明从家到小颖家有条路,小明为尽快走到小颖家,他该走 .
11.如果,那么的余角等于 ;的补角为 .
12.如图是一个正方体的表面展开图,则原正方体中与“戴”字所在的面相对的面上的汉字是 .
13.点A,B,C在同一直线上,若,则的中点与的中点的距离为 .
14.已知,,则的度数为 .
15.如图,将一副三角板(三角板和三角板)叠在一起,使两个直角顶点M、N重合,若,则 .
16.如图是由一些相同的小正方体搭成的几何体从正面和上面看到的形状图,搭这个几何体最少需要 个小正方体,最多需要 个小正方体.
三、解答题(满分56分)
17.如图,平面上有四个点A、B、C、D,根据下列语句画图.
(1)直线;
(2)画射线;
(3)连接、;
(4)在平面内找一点,使点到、、、四个点的距离和最小.
18.已知线段m、n.
(1)尺规作图:作线段,满足(保留作图痕迹,不用写作法);
(2)在(1)的条件下,点O是的中点,点C在线段上,且满足,当,时,求线段的长.
19.由8个棱长都为的小正方体搭成的几何体如左图.
(1)请利用图2中的网格画出这个几何体从正面看、从左面看和从上面看到的形状图.(一个网格为小立方体的一个面)
(2)图1中8个小正方体搭成的几何体的表面积(包括与地面接触的部分)是 cm2.
(3)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需要 个小立方块.
20.已知C为线段延长线上的点,M,N分别是的中点.
(1)如果,求线段的长;
(2)如果,求线段的长;
(3)如果,点P是的中点,求线段的长.
21.如图,是的平分线,是的平分线.
(1)如果,,那么是多少度?
(2)如果,,那么是多少度?
22.如图,,连接.
(1)用尺规作图法在射线上作,在射线上取点D使;
(2)连接,找一点P使它到四边形四个顶点的距离之和最小,并说明理由;
(3)设,
①当时,求的大小;
②当绕点O旋转任意角度时,请用表示和之间的数量关系,并说明理由.
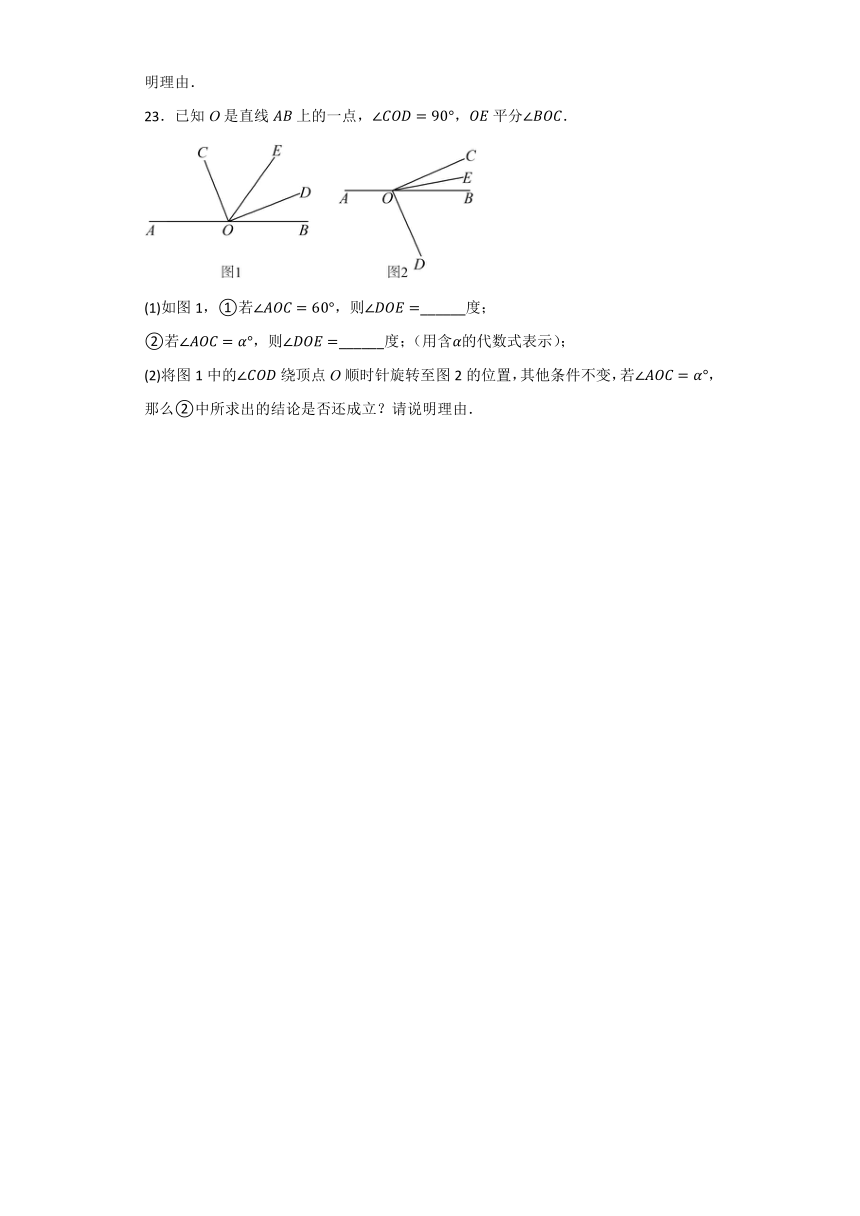
23.已知O是直线上的一点,,平分.
(1)如图1,①若,则______度;
②若,则______度;(用含的代数式表示);
(2)将图1中的绕顶点O顺时针旋转至图2的位置,其他条件不变,若,那么②中所求出的结论是否还成立?请说明理由.
参考答案
1.解:A.折叠后不能折成正方体,故本项不符合题意;
B.折叠后不能折成正方体,故本项不符合题意;
C.折叠后不能折成正方体,故本项不符合题意;
D.折叠后能折成正方体,故本项符合题意.
故选:D.
2.解:锯木板前,在木板两端固定两个点,用墨盒弹一根墨线然后再锯,这样做的数学道理是两点确定一条直线,
故选B.
3.解:根据题意得:其从上面看的形状图是
.
故选:C
4.解: A.用一个平面平行于三角形底面去截一个三棱柱,其截面是三角形,故该选项不符合题意;
B.用一个平面从上面顶点垂直去截一个圆锥,其截面是三角形,故该选项不符合题意;
C.用一个平面去截一个圆柱体,无论怎样,其截面都不可能是三角形,故该选项符合题意;
D.用一个平面去截一个长方体的角,其截面是三角形,故该选项不符合题意.
故选:C.
5.解:根据射线的定义,这直线上的每个点可以有两条射线,图中有四个点,即有8条射线,
故选B.
6.解:如图,当点在点的右侧时,
∵,且,
∴,
∴,
∵点M是线段的中点,
∴,
∴;
如图,当点在点的左侧时,
∵,且,
∴,
∴,
∵点M是线段的中点,
∴,
∴,
综上所述,线段的长为或.
故选:C
7.解:∵A在O点的北偏东的方向上,B在O点的南偏东的方向上,
∴,
故选B.
8.解:是的平分线,
,
,
,
是的平分线,
,
故选A.
9.解:,
故答案为:.
10.解:根据线段的基本事实,两点之间线段最短,
∴他该走①,
故答案为:①.
11.解:,
的余角为:,的补角为:,
故答案为:,.
12.解:由正方体的展开图特点可得:“罩”和“勤”相对;“手”和“口”相对;“戴”和“洗”相对;
故答案为:洗.
13.解:取的中点与的中点,
则
如图:;
如图:;
14.解:在内时,
∵,,
∴;
在外时,
∵,,
∴;
综上所述:的度数是或.
故答案为:或.
15.解:∵,,
∴,
∵,
∴,
故答案为:.
16.解:个数最少时:如图(图不唯一,第二列一个位置有2个即可,第三列有一个位置有3个即可);
;
个数最多时:如图:
;
故答案为:10;15.
17.(1)解:如图.
(2)解:如上图.
(3)解:如上图.
(4)解:如上图.
18.(1)解:如图,线段即为所求作.
(2)解:∵点O是的中点,
∴,
∵,
∴,
∵,,
∴.
19.(1)解:这个几何体从正面看、从左面看和从上面看到的形状图如下:
(2)图1中8个小正方体搭成的几何体的表面积(包括与地面接触的部分)是
,
故答案为:32
(3)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需9个小立方块.
故答案为:9
20.(1)解:∵M,N分别是的中点,,
∴,
∴;
(2)解:∵M,N分别是的中点,,
∴,
∴;
(3)解:∵,
∴,
∵点P是的中点,
∴,
由(2)得:,
.
21.(1)解:∵是的平分线,,
∴,
∵是的平分线,,
∴,
∴;
(2)∵是的平分线,,
∴,
∵,
∴,
∵是的平分线,
∴.
22.(1)解:如图,,点D即为所求;
;
(2)解:点P即为所求;
因为两点之间线段最短,所以最小;
∴点P到四边形四个顶点的距离之和最小.
(3)解:①∵时,
∴,
∴;
②当绕点O旋转任意角度时,,理由如下:
∵,,
∴,
∴,
∴.
∴.
23.解:(1)①∵,
∴,
∵,
∴,,
∵平分,
∴,
∴;
故答案为:;
②∵,
∴,
∵,
∴,
∴,
∵平分,
∴,
∴;
故答案为:;
(2)解:②中的结论还成立.
理由如下:
∵,,
∴
∵平分
∴
∵
∴.
单元综合达标测试题(附答案)
一、单选题(满分32分)
1.下列图形中是正方体表面展开图的是( )
A. B.
C. D.
2.如图,锯木板前,在木板两端固定两个点,用墨盒弹一根墨线然后再锯,这样做的数学道理是( )
A.两点之间线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
3.如图是由个完全相同的小正方体组成的几何体,其从上面看的形状图是( )
A. B. C. D.
4.用一个平面去截下列几何体,截得的平面图形不可能是三角形的是( )
A. B. C. D.
5.如图,共有射线( )
A.4条 B.8条 C.16条 D.32条
6.已知点A、B、C位于直线l上,其中线段,且,若点M是线段的中点,则线段的长为( )
A.1 B.3 C.5或1 D.1或4
7.一人在小岛O点处观察到轮船A在他北偏东的方向上,轮船B在他南偏东的方向上,那么此时的度数为( )
A. B. C. D.
8.如图,是的平分线,是的平分线,且,则为( )
A. B. C. D.
二、填空题(满分32分)
9.把化成用度表示的角是 .
10.如图,小明从家到小颖家有条路,小明为尽快走到小颖家,他该走 .
11.如果,那么的余角等于 ;的补角为 .
12.如图是一个正方体的表面展开图,则原正方体中与“戴”字所在的面相对的面上的汉字是 .
13.点A,B,C在同一直线上,若,则的中点与的中点的距离为 .
14.已知,,则的度数为 .
15.如图,将一副三角板(三角板和三角板)叠在一起,使两个直角顶点M、N重合,若,则 .
16.如图是由一些相同的小正方体搭成的几何体从正面和上面看到的形状图,搭这个几何体最少需要 个小正方体,最多需要 个小正方体.
三、解答题(满分56分)
17.如图,平面上有四个点A、B、C、D,根据下列语句画图.
(1)直线;
(2)画射线;
(3)连接、;
(4)在平面内找一点,使点到、、、四个点的距离和最小.
18.已知线段m、n.
(1)尺规作图:作线段,满足(保留作图痕迹,不用写作法);
(2)在(1)的条件下,点O是的中点,点C在线段上,且满足,当,时,求线段的长.
19.由8个棱长都为的小正方体搭成的几何体如左图.
(1)请利用图2中的网格画出这个几何体从正面看、从左面看和从上面看到的形状图.(一个网格为小立方体的一个面)
(2)图1中8个小正方体搭成的几何体的表面积(包括与地面接触的部分)是 cm2.
(3)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需要 个小立方块.
20.已知C为线段延长线上的点,M,N分别是的中点.
(1)如果,求线段的长;
(2)如果,求线段的长;
(3)如果,点P是的中点,求线段的长.
21.如图,是的平分线,是的平分线.
(1)如果,,那么是多少度?
(2)如果,,那么是多少度?
22.如图,,连接.
(1)用尺规作图法在射线上作,在射线上取点D使;
(2)连接,找一点P使它到四边形四个顶点的距离之和最小,并说明理由;
(3)设,
①当时,求的大小;
②当绕点O旋转任意角度时,请用表示和之间的数量关系,并说明理由.
23.已知O是直线上的一点,,平分.
(1)如图1,①若,则______度;
②若,则______度;(用含的代数式表示);
(2)将图1中的绕顶点O顺时针旋转至图2的位置,其他条件不变,若,那么②中所求出的结论是否还成立?请说明理由.
参考答案
1.解:A.折叠后不能折成正方体,故本项不符合题意;
B.折叠后不能折成正方体,故本项不符合题意;
C.折叠后不能折成正方体,故本项不符合题意;
D.折叠后能折成正方体,故本项符合题意.
故选:D.
2.解:锯木板前,在木板两端固定两个点,用墨盒弹一根墨线然后再锯,这样做的数学道理是两点确定一条直线,
故选B.
3.解:根据题意得:其从上面看的形状图是
.
故选:C
4.解: A.用一个平面平行于三角形底面去截一个三棱柱,其截面是三角形,故该选项不符合题意;
B.用一个平面从上面顶点垂直去截一个圆锥,其截面是三角形,故该选项不符合题意;
C.用一个平面去截一个圆柱体,无论怎样,其截面都不可能是三角形,故该选项符合题意;
D.用一个平面去截一个长方体的角,其截面是三角形,故该选项不符合题意.
故选:C.
5.解:根据射线的定义,这直线上的每个点可以有两条射线,图中有四个点,即有8条射线,
故选B.
6.解:如图,当点在点的右侧时,
∵,且,
∴,
∴,
∵点M是线段的中点,
∴,
∴;
如图,当点在点的左侧时,
∵,且,
∴,
∴,
∵点M是线段的中点,
∴,
∴,
综上所述,线段的长为或.
故选:C
7.解:∵A在O点的北偏东的方向上,B在O点的南偏东的方向上,
∴,
故选B.
8.解:是的平分线,
,
,
,
是的平分线,
,
故选A.
9.解:,
故答案为:.
10.解:根据线段的基本事实,两点之间线段最短,
∴他该走①,
故答案为:①.
11.解:,
的余角为:,的补角为:,
故答案为:,.
12.解:由正方体的展开图特点可得:“罩”和“勤”相对;“手”和“口”相对;“戴”和“洗”相对;
故答案为:洗.
13.解:取的中点与的中点,
则
如图:;
如图:;
14.解:在内时,
∵,,
∴;
在外时,
∵,,
∴;
综上所述:的度数是或.
故答案为:或.
15.解:∵,,
∴,
∵,
∴,
故答案为:.
16.解:个数最少时:如图(图不唯一,第二列一个位置有2个即可,第三列有一个位置有3个即可);
;
个数最多时:如图:
;
故答案为:10;15.
17.(1)解:如图.
(2)解:如上图.
(3)解:如上图.
(4)解:如上图.
18.(1)解:如图,线段即为所求作.
(2)解:∵点O是的中点,
∴,
∵,
∴,
∵,,
∴.
19.(1)解:这个几何体从正面看、从左面看和从上面看到的形状图如下:
(2)图1中8个小正方体搭成的几何体的表面积(包括与地面接触的部分)是
,
故答案为:32
(3)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需9个小立方块.
故答案为:9
20.(1)解:∵M,N分别是的中点,,
∴,
∴;
(2)解:∵M,N分别是的中点,,
∴,
∴;
(3)解:∵,
∴,
∵点P是的中点,
∴,
由(2)得:,
.
21.(1)解:∵是的平分线,,
∴,
∵是的平分线,,
∴,
∴;
(2)∵是的平分线,,
∴,
∵,
∴,
∵是的平分线,
∴.
22.(1)解:如图,,点D即为所求;
;
(2)解:点P即为所求;
因为两点之间线段最短,所以最小;
∴点P到四边形四个顶点的距离之和最小.
(3)解:①∵时,
∴,
∴;
②当绕点O旋转任意角度时,,理由如下:
∵,,
∴,
∴,
∴.
∴.
23.解:(1)①∵,
∴,
∵,
∴,,
∵平分,
∴,
∴;
故答案为:;
②∵,
∴,
∵,
∴,
∴,
∵平分,
∴,
∴;
故答案为:;
(2)解:②中的结论还成立.
理由如下:
∵,,
∴
∵平分
∴
∵
∴.
