11.6轴对称 课件 数学沪教版(上海)七年级第一学期(共16张PPT)
文档属性
| 名称 | 11.6轴对称 课件 数学沪教版(上海)七年级第一学期(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 23:06:30 | ||
图片预览




文档简介
(共16张PPT)
11.6轴对称
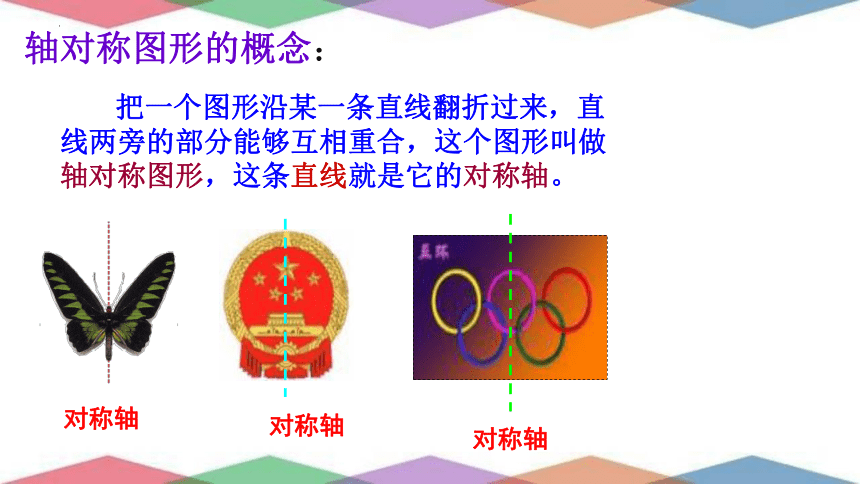
轴对称图形的概念:
把一个图形沿某一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线就是它的对称轴。
对称轴
对称轴
对称轴
你能发现它们有什
么共同的特征吗?
轴对称:把一个图形沿着某一条直线翻折,如果它能与另一个图形完全重合,那么叫做这两个图形关于这条直线成轴对称。这条直线叫做对称轴。折叠后重合的点是对应点,叫做对称点。
1、轴对称:
把一个图形沿着某一条直线翻折,如果它能与另一个图形完全重合,那么叫做这两个图形关于这条直线成轴对称。这条直线叫做对称轴。折叠后重合的点是对应点,叫做对称点。
2、轴对称图形:
把一个图形沿某一条直线翻折过来,如果直线两旁的部分能够完全重合,这个图形叫做轴对称图形,这条直线就是它的对称轴。
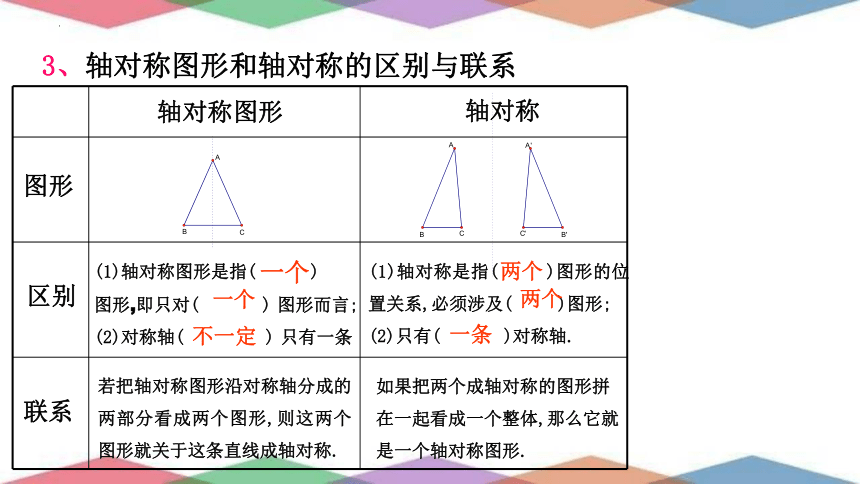
3、轴对称图形和轴对称的区别与联系
轴对称图形
轴对称
区别
联系
图形
(1)轴对称图形是指( )
图形,即只对( ) 图形而言;
(2)对称轴( ) 只有一条
(1)轴对称是指( )图形的位置关系,必须涉及( )图形;
(2)只有( )对称轴.
若把轴对称图形沿对称轴分成的两部分看成两个图形,则这两个图形就关于这条直线成轴对称.
如果把两个成轴对称的图形拼
在一起看成一个整体,那么它就
是一个轴对称图形.
一个
一个
不一定
两个
两个
一条
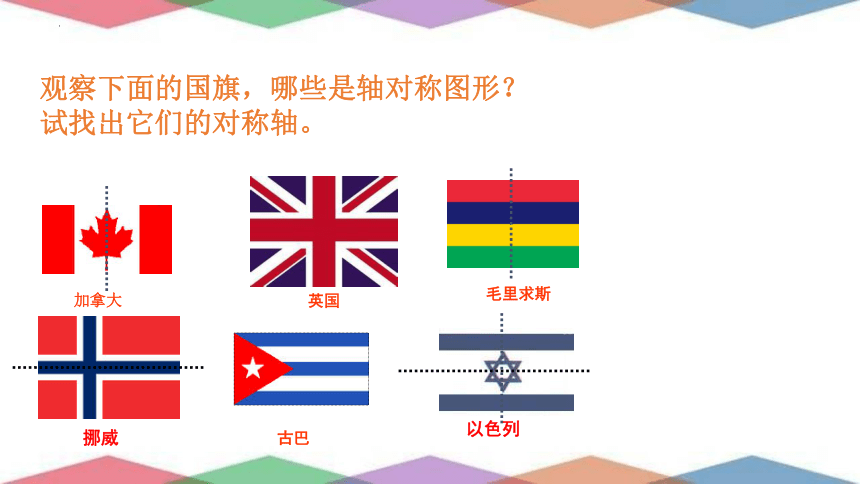
观察下面的国旗,哪些是轴对称图形?
试找出它们的对称轴。
加拿大
英国
毛里求斯
古巴
挪威
以色列
试一试
你能找出下面正五边形和正六边形的对称轴吗?
对象 是否为轴对称图形 对称轴 是否为中心 对称图形 对称中心
角
线段
等腰三角形
等边三角形
圆
矩形
正方形 菱形 平行四边形 正n边形 等腰梯形
是(1)
角平分线所在直线
否
是(1)
线段的垂直平分线
是
否
否
否
是
是
是
是
是
偶是奇否
是(1)
底边上的高(底边上的中线、
顶角角平分线)所在直线
线段中点
圆心
对角线
交点
是(3)
各边上的高(底边上的中线、
各角角平分线)所在直线
是(无数)
直径所在直线
是(2)
对边中点所连直线
是(4)
对边中点所连直线、
对角线所在直线
是(2)
对角线所在直线
否
是(n)
是(1)
上下底边中点所连直线
观察下面的图形,你能发现它们有什么共同的特征吗?
细心观察
下面每对图形呢
例题讲解
例1 如图 5-6,已知直线l及直线外一点P,求作点P',使它与点P关于直线l对称.
作法:1. 过点P作 PQ⊥l,交l于点 O.
.
P
O
P'
l
Q
图5-6
2. 在直线 PQ上,截取 OP'=OP.则点P'即为所求作的点.
如图5-7,已知线段AB和直线l ,作出与线段AB关于直线l 对称的图形.
l
A
B
图5-7
A'
B'
)
)
例2 如图5-8,已知三角形ABC和直线l,作出与三角形 ABC关于直线l对称的图形.
例题讲解
图5-8
作法:1. 过点A作直线l的垂线,垂足为点O,在垂线上截取OA'= OA,点A'就是点A关于直线l的对应点.
画好三角形 A'B'C'后,若将纸沿直线l对折两个三角形会重合吗?
2. 类似地,分别作出点B,C关于直线l的对应点 B',C'.
3. 连接A'B',B'C',C'A'得到的三角形A'B'C'即为所求.
分析:要作三角形ABC关于直线l的对称图形,只要作出三角形的顶点A,B,C关于直线l的对应点A',B',C',连接这些对应点,得到的三角形A'B'C'就是三角形ABC 关于直线l对称的图形.
l
A
C
A'
B'
C'
O
B
获取新知
作已知图形关于已知直线对称的图形的一般步聚:
1、找点
2、画点
3、连线
(确定图形中的一些特殊点);
(画出特殊点关于已知直线的对称点);
(连接对称点)。
随堂演练
A
D
谢谢观看
11.6轴对称
轴对称图形的概念:
把一个图形沿某一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线就是它的对称轴。
对称轴
对称轴
对称轴
你能发现它们有什
么共同的特征吗?
轴对称:把一个图形沿着某一条直线翻折,如果它能与另一个图形完全重合,那么叫做这两个图形关于这条直线成轴对称。这条直线叫做对称轴。折叠后重合的点是对应点,叫做对称点。
1、轴对称:
把一个图形沿着某一条直线翻折,如果它能与另一个图形完全重合,那么叫做这两个图形关于这条直线成轴对称。这条直线叫做对称轴。折叠后重合的点是对应点,叫做对称点。
2、轴对称图形:
把一个图形沿某一条直线翻折过来,如果直线两旁的部分能够完全重合,这个图形叫做轴对称图形,这条直线就是它的对称轴。
3、轴对称图形和轴对称的区别与联系
轴对称图形
轴对称
区别
联系
图形
(1)轴对称图形是指( )
图形,即只对( ) 图形而言;
(2)对称轴( ) 只有一条
(1)轴对称是指( )图形的位置关系,必须涉及( )图形;
(2)只有( )对称轴.
若把轴对称图形沿对称轴分成的两部分看成两个图形,则这两个图形就关于这条直线成轴对称.
如果把两个成轴对称的图形拼
在一起看成一个整体,那么它就
是一个轴对称图形.
一个
一个
不一定
两个
两个
一条
观察下面的国旗,哪些是轴对称图形?
试找出它们的对称轴。
加拿大
英国
毛里求斯
古巴
挪威
以色列
试一试
你能找出下面正五边形和正六边形的对称轴吗?
对象 是否为轴对称图形 对称轴 是否为中心 对称图形 对称中心
角
线段
等腰三角形
等边三角形
圆
矩形
正方形 菱形 平行四边形 正n边形 等腰梯形
是(1)
角平分线所在直线
否
是(1)
线段的垂直平分线
是
否
否
否
是
是
是
是
是
偶是奇否
是(1)
底边上的高(底边上的中线、
顶角角平分线)所在直线
线段中点
圆心
对角线
交点
是(3)
各边上的高(底边上的中线、
各角角平分线)所在直线
是(无数)
直径所在直线
是(2)
对边中点所连直线
是(4)
对边中点所连直线、
对角线所在直线
是(2)
对角线所在直线
否
是(n)
是(1)
上下底边中点所连直线
观察下面的图形,你能发现它们有什么共同的特征吗?
细心观察
下面每对图形呢
例题讲解
例1 如图 5-6,已知直线l及直线外一点P,求作点P',使它与点P关于直线l对称.
作法:1. 过点P作 PQ⊥l,交l于点 O.
.
P
O
P'
l
Q
图5-6
2. 在直线 PQ上,截取 OP'=OP.则点P'即为所求作的点.
如图5-7,已知线段AB和直线l ,作出与线段AB关于直线l 对称的图形.
l
A
B
图5-7
A'
B'
)
)
例2 如图5-8,已知三角形ABC和直线l,作出与三角形 ABC关于直线l对称的图形.
例题讲解
图5-8
作法:1. 过点A作直线l的垂线,垂足为点O,在垂线上截取OA'= OA,点A'就是点A关于直线l的对应点.
画好三角形 A'B'C'后,若将纸沿直线l对折两个三角形会重合吗?
2. 类似地,分别作出点B,C关于直线l的对应点 B',C'.
3. 连接A'B',B'C',C'A'得到的三角形A'B'C'即为所求.
分析:要作三角形ABC关于直线l的对称图形,只要作出三角形的顶点A,B,C关于直线l的对应点A',B',C',连接这些对应点,得到的三角形A'B'C'就是三角形ABC 关于直线l对称的图形.
l
A
C
A'
B'
C'
O
B
获取新知
作已知图形关于已知直线对称的图形的一般步聚:
1、找点
2、画点
3、连线
(确定图形中的一些特殊点);
(画出特殊点关于已知直线的对称点);
(连接对称点)。
随堂演练
A
D
谢谢观看
