8.3 实际问题与二元一次方程组(1)教学课件(共21张PPT) 2022-2023学年人教版数学七年级下册
文档属性
| 名称 | 8.3 实际问题与二元一次方程组(1)教学课件(共21张PPT) 2022-2023学年人教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 580.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
第1课时
8.3 实际问题与二元一次方程组
学习目标
1.能够根据具体的数量关系,列出二元一次方程组并解决简单的实际问题;
2.会利用二元一次方程组解决和、差、倍、分等问题;
3.经历“分析数量关系→设未知数→列方程组→解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数问题的数学模型;
4.通过探究实际问题,进一步认识利用二元一次方程组解决问题的基本过程,体会数学的应用价值,提高分析问题、解决问题的能力.
实际问题与二元一次方程组
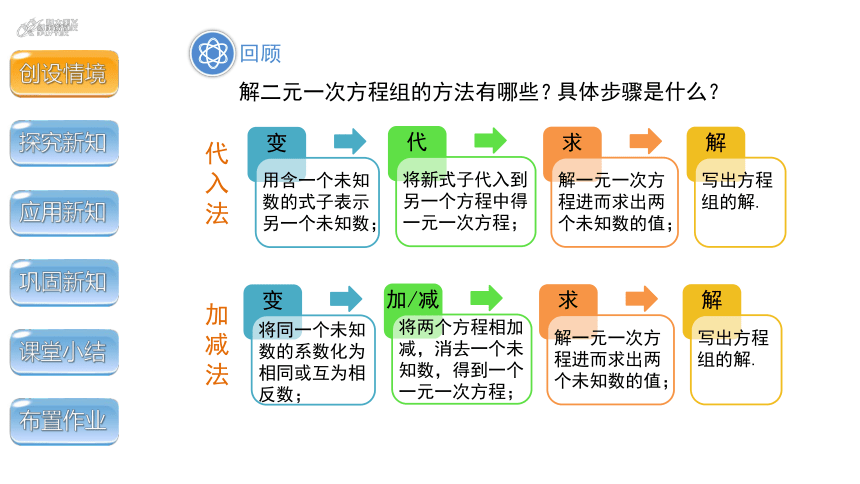
回顾
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
解二元一次方程组的方法有哪些?
代入法
加减法
具体步骤是什么?
变
用含一个未知数的式子表示另一个未知数;
代
将新式子代入到另一个方程中得一元一次方程;
求
解一元一次方程进而求出两个未知数的值;
解
写出方程组的解.
变
将同一个未知数的系数化为
相同或互为相反数;
加/减
将两个方程相加减,消去一个未知数,得到一个 一元一次方程;
求
解一元一次方程进而求出两个未知数的值;
解
写出方程组的解.
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
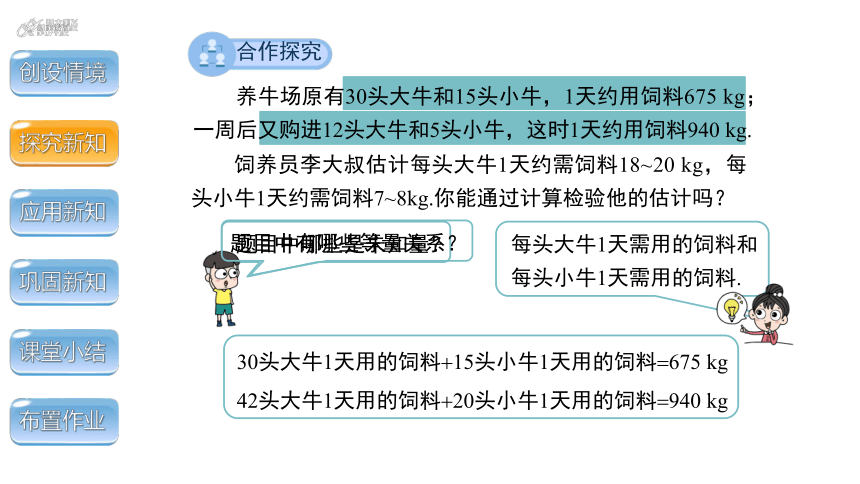
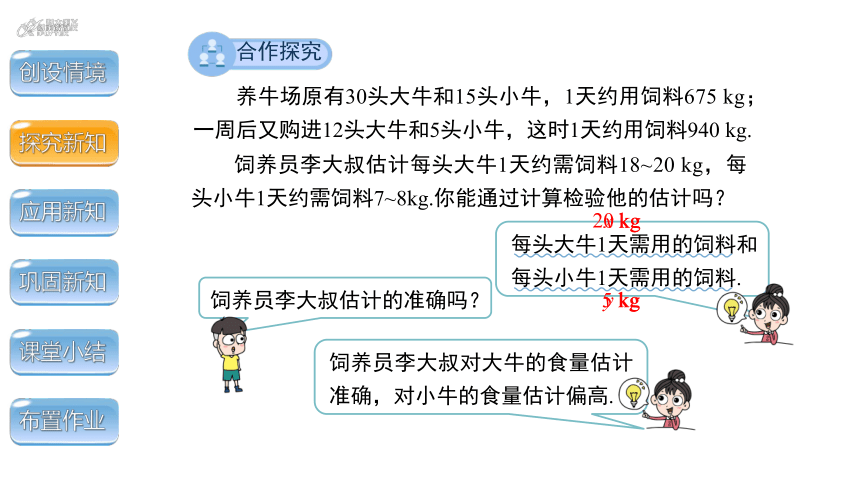
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.
饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8kg.你能通过计算检验他的估计吗?
每头大牛1天需用的饲料和
每头小牛1天需用的饲料.
题目中哪些是未知量?
题目中有哪些等量关系?
30头大牛1天用的饲料 15头小牛1天用的饲料 675 kg
42头大牛1天用的饲料 20头小牛1天用的饲料 940 kg
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
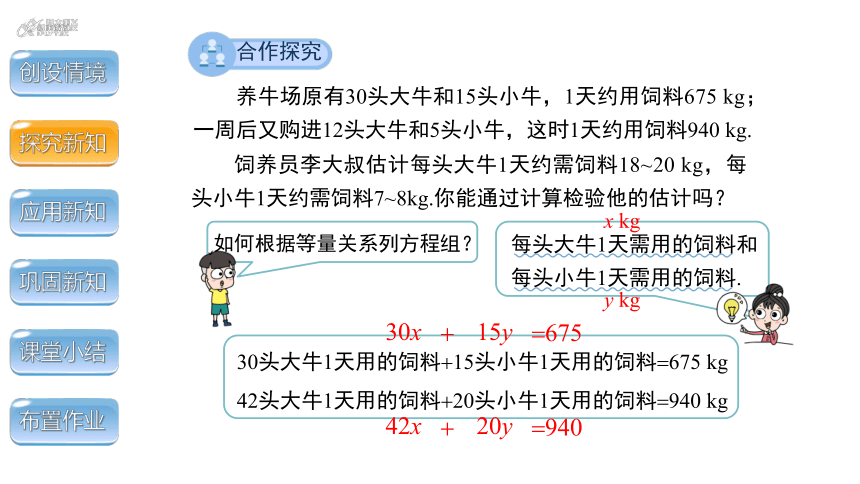
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.
饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8kg.你能通过计算检验他的估计吗?
每头大牛1天需用的饲料和
每头小牛1天需用的饲料.
如何根据等量关系列方程组?
30头大牛1天用的饲料 15头小牛1天用的饲料 675 kg
42头大牛1天用的饲料 20头小牛1天用的饲料 940 kg
x kg
y kg
30x
15y
675
42x
20y
940
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
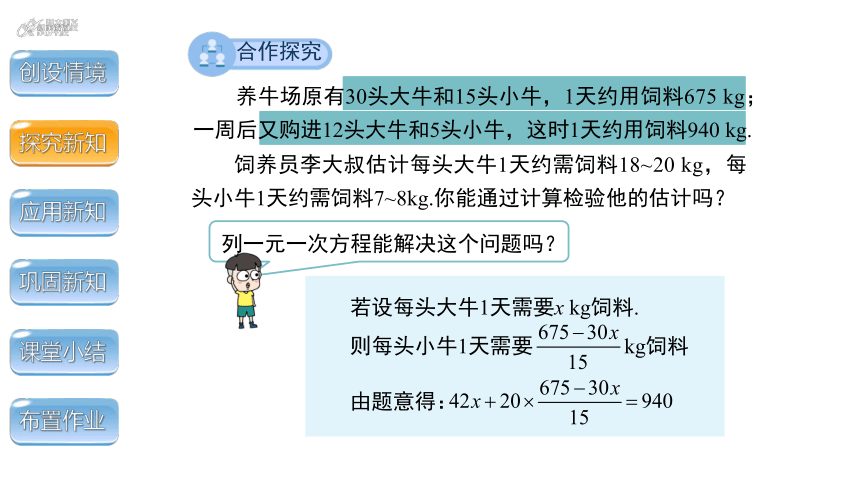
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.
饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8kg.你能通过计算检验他的估计吗?
列一元一次方程能解决这个问题吗?
若设每头大牛1天需要x kg饲料.
则每头小牛1天需要 kg饲料
由题意得:
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如何解这个方程组呢?
①
②
直接消元
解:① 4,得120x 60y 2700,③
② 3,得126x 60y 2820,④
④ ③,得6x 120,解得x 20.
把x 20代入①,得30 20 15y 675,
解得y 5.
所以这个方程组的解是
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如何解这个方程组呢?
先化简再消元
解:方程组可化简为
由①,得y 45 2x,③
把③代入②,得21x 10(45 2x) 470,
解得x 20.
把x 20代入③,得y 5.
所以这个方程组的解是
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.
饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8kg.你能通过计算检验他的估计吗?
每头大牛1天需用的饲料和
每头小牛1天需用的饲料.
饲养员李大叔估计的准确吗?
x kg
y kg
20 kg
5 kg
饲养员李大叔对大牛的食量估计准确,对小牛的食量估计偏高.
想一想
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲、乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人.
42,
20.
则:
x ,
y .
解得:
所以李大叔应聘请甲种饲养员 人,乙种饲养员 人.
8x
5y
4x
2y
4
2
4
2
列二元一次方程组解应用题的一般步骤
归纳
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
1.审题:认真审题,分清题中的已知量、未知量,并明确它们之间的等量关系;
2.设元:用字母表示题目中的未知数;
3.列方程组:根据题中的等量关系列出方程组;
4.解方程组:解方程组,求出未知数的值;
5.检验并答:检验所求的解是否符合实际意义,然后作答.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例1 某单位组织200人到甲、乙两地旅游,到甲地的人数比到乙地的人数的2倍少10人,到两地参加旅游的人数各是多少?
到甲地旅游的人数 到乙地旅游的人数 200
到甲地旅游的人数 到乙地旅游的人数 2 10
分析:
解:设到甲、乙两地旅游的人数分别是x人、y人.
由题意得:
解得:
答:到甲、乙两地旅游的人数分别是130人、70人.
1.基本数量关系:各部分数量之和=全部数量;
2.方法:明显的关键词,如比、是、等于、多、 少、倍、共、和、几分之几等;
隐含的关键词,总面积,总数量,总钱数等.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例1 某单位组织200人到甲、乙两地旅游,到甲地的人数比到乙地的人数的2倍少10人,到两地参加旅游的人数各是多少?
解:设到甲、乙两地旅游的人数分别是x人、y人.
由题意得:
解得:
答:到甲、乙两地旅游的人数分别是130人、70人.
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
1.甲、乙两数的和为42,甲数的3倍等于乙数的4倍,求甲、乙两数,设甲数为x,乙数为y,则下列方程组正确的是( )
A. B.
C. D.
B
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
2.用4700张纸装订成两种挂历共500本,其中甲种每本7张纸,乙种每本13张纸.若甲种挂历有x本,乙种挂历有y本,则下面所列方程组正确的是( )
A. B.
C. D.
B
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
3.某工厂有60名工人,生产某种由一个螺栓套两个螺母的配套产品,每人每天可生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,才能使生产出的螺栓和螺母刚好配套?
分析:
解:设生产螺栓、螺母人数分别是x人、y人.
由题意得:
解得:
答:生产螺栓、螺母人数分别是25人、35人.
螺栓 螺母
所需人数
生产总量
x
y
14x
20y
60
1 2
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
4.某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐?
解:(1)设1个大餐厅和1个小餐厅分别可供x名、y名学生就餐.
由题意得:
解得:
所以1个大餐厅和1个小餐厅分别可供960名、360名学生就餐.
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
4.某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐.
(2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.
解:(2)若7个餐厅同时开放,则:
5 960 2 360 5520,
5520 5300.
所以若7个餐厅同时开放,可以供应全校5300名学生就餐.
找等量关系的常见方法
1.基本数量关系:各部分数量之和=全部数量;
2.方法:明显的关键词,如比、是、等于、多、 少、倍、共、和、几分之几等;
隐含的关键词,总面积,总数量,总钱数等.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
列二元一次方程组解应用题的一般步骤
1.审题:认真审题,分清题中的已知量、未知量,并明确它们之间的等量关系;
2.设元:用字母表示题目中的未知数;
3.列方程组:根据题中的等量关系列出方程组;
4.解方程组:解方程组,求出未知数的值;
5.检验并答:检验所求的解是否符合实际意义,然后作答.
实际问题与二元一次方程组
布置作业
教科书第102页
习题8.3第4、5题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
第1课时
8.3 实际问题与二元一次方程组
学习目标
1.能够根据具体的数量关系,列出二元一次方程组并解决简单的实际问题;
2.会利用二元一次方程组解决和、差、倍、分等问题;
3.经历“分析数量关系→设未知数→列方程组→解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数问题的数学模型;
4.通过探究实际问题,进一步认识利用二元一次方程组解决问题的基本过程,体会数学的应用价值,提高分析问题、解决问题的能力.
实际问题与二元一次方程组
回顾
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
解二元一次方程组的方法有哪些?
代入法
加减法
具体步骤是什么?
变
用含一个未知数的式子表示另一个未知数;
代
将新式子代入到另一个方程中得一元一次方程;
求
解一元一次方程进而求出两个未知数的值;
解
写出方程组的解.
变
将同一个未知数的系数化为
相同或互为相反数;
加/减
将两个方程相加减,消去一个未知数,得到一个 一元一次方程;
求
解一元一次方程进而求出两个未知数的值;
解
写出方程组的解.
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.
饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8kg.你能通过计算检验他的估计吗?
每头大牛1天需用的饲料和
每头小牛1天需用的饲料.
题目中哪些是未知量?
题目中有哪些等量关系?
30头大牛1天用的饲料 15头小牛1天用的饲料 675 kg
42头大牛1天用的饲料 20头小牛1天用的饲料 940 kg
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.
饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8kg.你能通过计算检验他的估计吗?
每头大牛1天需用的饲料和
每头小牛1天需用的饲料.
如何根据等量关系列方程组?
30头大牛1天用的饲料 15头小牛1天用的饲料 675 kg
42头大牛1天用的饲料 20头小牛1天用的饲料 940 kg
x kg
y kg
30x
15y
675
42x
20y
940
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.
饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8kg.你能通过计算检验他的估计吗?
列一元一次方程能解决这个问题吗?
若设每头大牛1天需要x kg饲料.
则每头小牛1天需要 kg饲料
由题意得:
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如何解这个方程组呢?
①
②
直接消元
解:① 4,得120x 60y 2700,③
② 3,得126x 60y 2820,④
④ ③,得6x 120,解得x 20.
把x 20代入①,得30 20 15y 675,
解得y 5.
所以这个方程组的解是
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如何解这个方程组呢?
先化简再消元
解:方程组可化简为
由①,得y 45 2x,③
把③代入②,得21x 10(45 2x) 470,
解得x 20.
把x 20代入③,得y 5.
所以这个方程组的解是
合作探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
养牛场原有30头大牛和15头小牛,1天约用饲料675 kg;一周后又购进12头大牛和5头小牛,这时1天约用饲料940 kg.
饲养员李大叔估计每头大牛1天约需饲料18~20 kg,每头小牛1天约需饲料7~8kg.你能通过计算检验他的估计吗?
每头大牛1天需用的饲料和
每头小牛1天需用的饲料.
饲养员李大叔估计的准确吗?
x kg
y kg
20 kg
5 kg
饲养员李大叔对大牛的食量估计准确,对小牛的食量估计偏高.
想一想
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲、乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人.
42,
20.
则:
x ,
y .
解得:
所以李大叔应聘请甲种饲养员 人,乙种饲养员 人.
8x
5y
4x
2y
4
2
4
2
列二元一次方程组解应用题的一般步骤
归纳
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
1.审题:认真审题,分清题中的已知量、未知量,并明确它们之间的等量关系;
2.设元:用字母表示题目中的未知数;
3.列方程组:根据题中的等量关系列出方程组;
4.解方程组:解方程组,求出未知数的值;
5.检验并答:检验所求的解是否符合实际意义,然后作答.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例1 某单位组织200人到甲、乙两地旅游,到甲地的人数比到乙地的人数的2倍少10人,到两地参加旅游的人数各是多少?
到甲地旅游的人数 到乙地旅游的人数 200
到甲地旅游的人数 到乙地旅游的人数 2 10
分析:
解:设到甲、乙两地旅游的人数分别是x人、y人.
由题意得:
解得:
答:到甲、乙两地旅游的人数分别是130人、70人.
1.基本数量关系:各部分数量之和=全部数量;
2.方法:明显的关键词,如比、是、等于、多、 少、倍、共、和、几分之几等;
隐含的关键词,总面积,总数量,总钱数等.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例1 某单位组织200人到甲、乙两地旅游,到甲地的人数比到乙地的人数的2倍少10人,到两地参加旅游的人数各是多少?
解:设到甲、乙两地旅游的人数分别是x人、y人.
由题意得:
解得:
答:到甲、乙两地旅游的人数分别是130人、70人.
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
1.甲、乙两数的和为42,甲数的3倍等于乙数的4倍,求甲、乙两数,设甲数为x,乙数为y,则下列方程组正确的是( )
A. B.
C. D.
B
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
2.用4700张纸装订成两种挂历共500本,其中甲种每本7张纸,乙种每本13张纸.若甲种挂历有x本,乙种挂历有y本,则下面所列方程组正确的是( )
A. B.
C. D.
B
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
3.某工厂有60名工人,生产某种由一个螺栓套两个螺母的配套产品,每人每天可生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,才能使生产出的螺栓和螺母刚好配套?
分析:
解:设生产螺栓、螺母人数分别是x人、y人.
由题意得:
解得:
答:生产螺栓、螺母人数分别是25人、35人.
螺栓 螺母
所需人数
生产总量
x
y
14x
20y
60
1 2
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
4.某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐?
解:(1)设1个大餐厅和1个小餐厅分别可供x名、y名学生就餐.
由题意得:
解得:
所以1个大餐厅和1个小餐厅分别可供960名、360名学生就餐.
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
4.某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐.
(2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.
解:(2)若7个餐厅同时开放,则:
5 960 2 360 5520,
5520 5300.
所以若7个餐厅同时开放,可以供应全校5300名学生就餐.
找等量关系的常见方法
1.基本数量关系:各部分数量之和=全部数量;
2.方法:明显的关键词,如比、是、等于、多、 少、倍、共、和、几分之几等;
隐含的关键词,总面积,总数量,总钱数等.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
列二元一次方程组解应用题的一般步骤
1.审题:认真审题,分清题中的已知量、未知量,并明确它们之间的等量关系;
2.设元:用字母表示题目中的未知数;
3.列方程组:根据题中的等量关系列出方程组;
4.解方程组:解方程组,求出未知数的值;
5.检验并答:检验所求的解是否符合实际意义,然后作答.
实际问题与二元一次方程组
布置作业
教科书第102页
习题8.3第4、5题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
