7.1.2 平面直角坐标系 课件(共22张PPT)2022-2023学年数学人教版七年级下册
文档属性
| 名称 | 7.1.2 平面直角坐标系 课件(共22张PPT)2022-2023学年数学人教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 543.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 11:01:23 | ||
图片预览


文档简介
(共22张PPT)
7.1.2 平面直角坐标系
学习目标
平面直角坐标系
1.理解平面直角坐标系的相关概念.
2.掌握平面直角坐标系内点与坐标是一一对应的.
3.理解在平面直角坐标系中四个象限的点对应坐标的符号特征.
4.能运用点的坐标的符号特征解决问题,进一步体会数形结合思想的作用.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
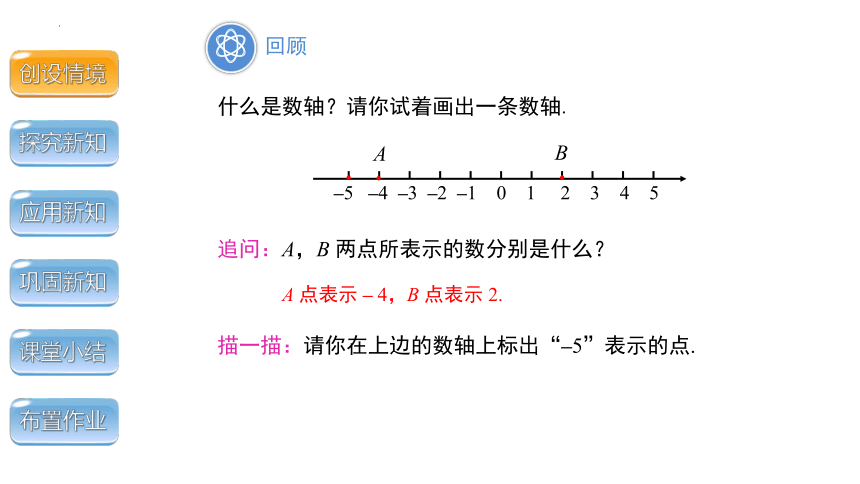
什么是数轴?请你试着画出一条数轴.
–5 –4 –3 –2 –1 0 1 2 3 4 5
回顾
追问:A,B 两点所表示的数分别是什么?
A
B
·
·
A 点表示 – 4,B 点表示 2.
描一描:请你在上边的数轴上标出“–5”表示的点.
·
–5 –4 –3 –2 –1 0 1 2 3 4 5
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
·
·
数轴上的点与坐标有怎样的关系?
“一一对应”的
思考
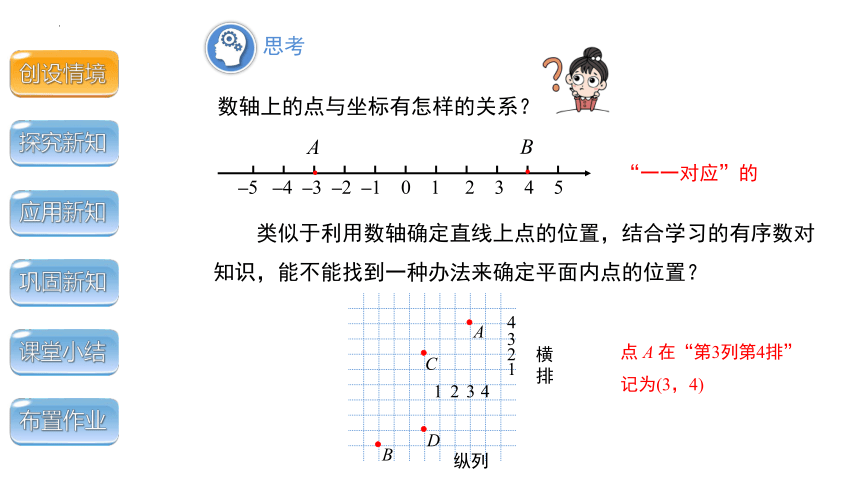
类似于利用数轴确定直线上点的位置,结合学习的有序数对知识,能不能找到一种办法来确定平面内点的位置?
B
A
D
C
横
排
纵列
4
3
2
1
3
2
4
1
点 A 在“第3列第4排”
记为(3,4)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
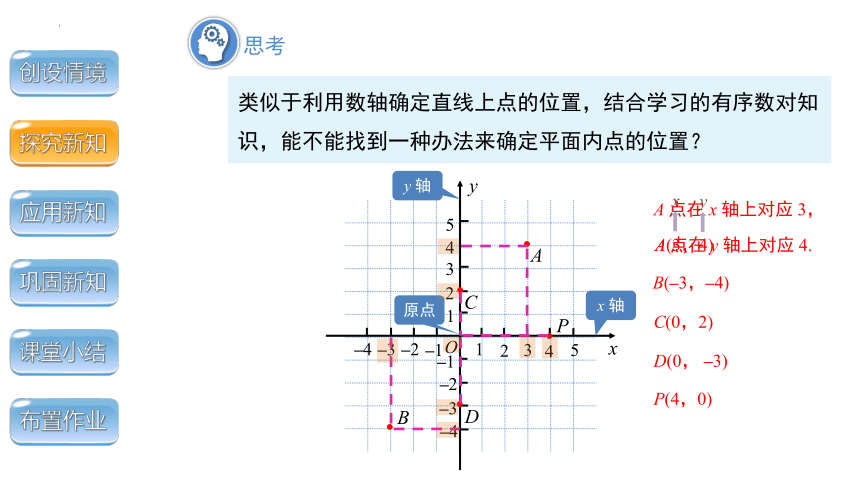
类似于利用数轴确定直线上点的位置,结合学习的有序数对知识,能不能找到一种办法来确定平面内点的位置?
A
B
D
C
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
4
3
2
1
5
–4
x 轴
x
y 轴
y
原点
A 点在 x 轴上对应 3,
A(3,4)
B(–3,–4)
C(0,2)
D(0, –3)
P
P(4,0)
A 点在 y 轴上对应 4.
x
y
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
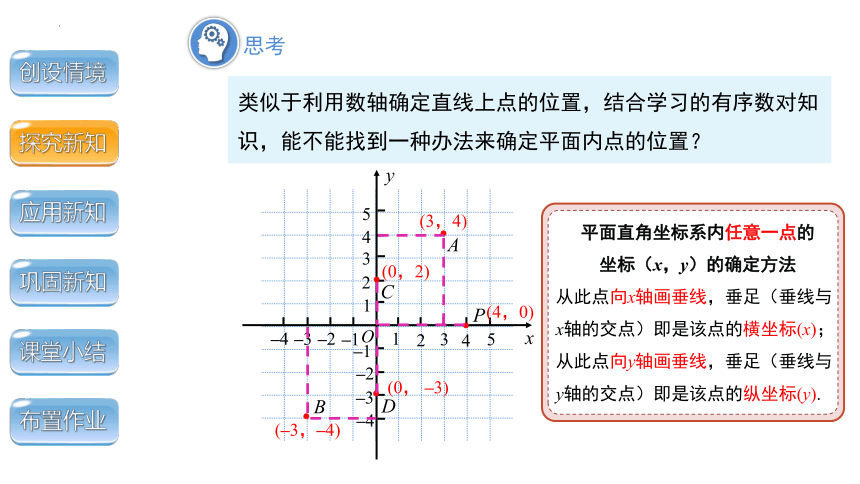
类似于利用数轴确定直线上点的位置,结合学习的有序数对知识,能不能找到一种办法来确定平面内点的位置?
A
B
D
C
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
4
3
2
1
5
–4
x
y
(3,4)
(–3,–4)
(0,2)
(0, –3)
P
(4,0)
平面直角坐标系内任意一点的
坐标(x,y)的确定方法
从此点向x轴画垂线,垂足(垂线与x轴的交点)即是该点的横坐标(x);
从此点向y轴画垂线,垂足(垂线与y轴的交点)即是该点的纵坐标(y).
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
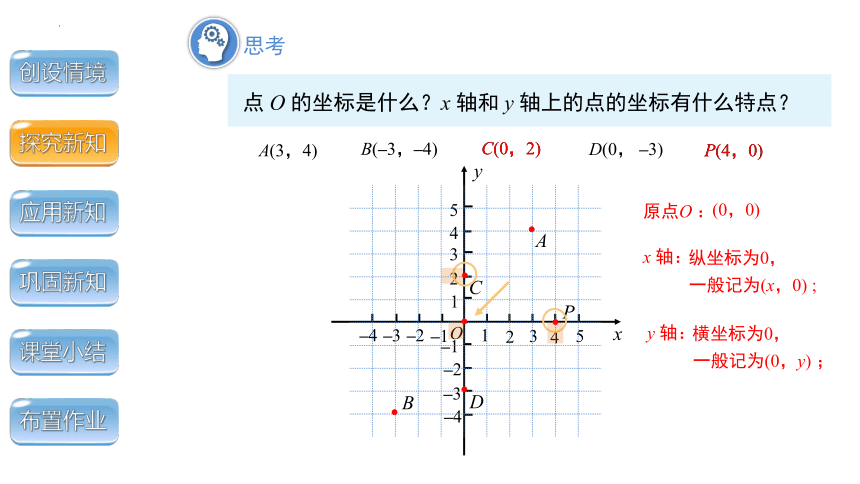
点 O 的坐标是什么?x 轴和 y 轴上的点的坐标有什么特点?
A
B
D
C
x
y
A(3,4)
B(–3,–4)
C(0,2)
D(0, –3)
原点O :
y 轴:
横坐标为0,
一般记为(0,y) ;
x 轴:
纵坐标为0,
一般记为(x,0) ;
C(0,2)
P(4,0)
P(4,0)
P
(0,0)
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
x
y
观察
x 轴
y 轴
原点
第一象限
Ⅰ
第二象限
Ⅱ
第三象限
Ⅲ
第四象限
Ⅳ
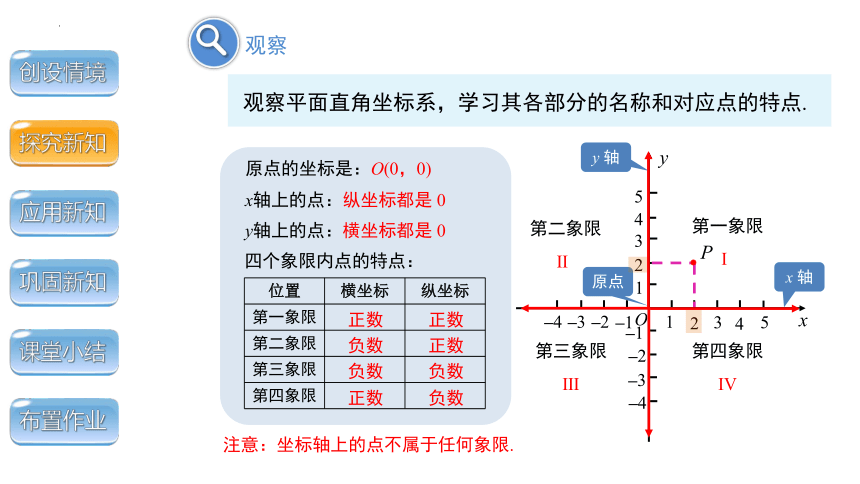
观察平面直角坐标系,学习其各部分的名称和对应点的特点.
P
原点的坐标是:O(0,0)
x轴上的点:纵坐标都是 0
y轴上的点:横坐标都是 0
四个象限内点的特点:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
注意:坐标轴上的点不属于任何象限.
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
观察与思考
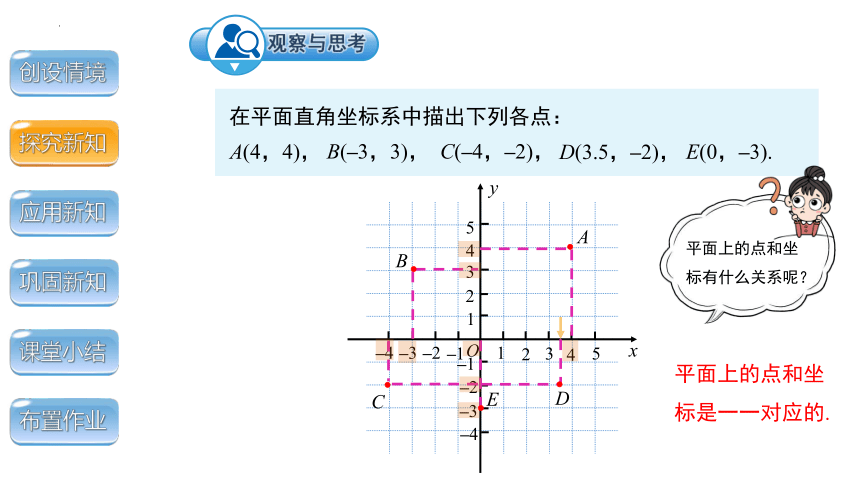
在平面直角坐标系中描出下列各点:
y
A
B
C
D
E
平面上的点和坐标有什么关系呢?
平面上的点和坐标是一一对应的.
x
A(4,4),
B(–3,3),
C(–4,–2),
D(3.5,–2),
E(0,–3).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
如图,正方形 ABCD 的边长为 6,如果以点 A 为原点,AB 所在直线为 x 轴,建立平面直角坐标系,那么 y 轴是哪条线?
探究
x
C
B
A
D
请你写出正方形的顶点 A,B,C,D 的坐标.
A(0,0)
B(6,0)
C(6,6)
D(0,6)
试着再建立一个平面直角坐标系,这时正方形的顶点 A,B,C,D 的坐标又分别是什么?
y
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
1.在平面直角坐标系中描出下列各点:
A(4,5) ,B(–2,3) ,C(–4,–1) ,D(2.5,–2) ,E(0,–4) .
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
A
B
C
D
E
x
y
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
2.点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a>0,b<0 时,点 M 位于第几象限?
(2) 当 ab>0 时,点M 位于第几象限?
(3) 当 a 为任意实数,且 b<0 时,点 M 位于第几象限?
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
2.点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a>0,b<0 时,点 M 位于第几象限?
第四象限
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
a>0,b>0 时,点M在第一象限;
2.点 M(a,b) 为平面直角坐标系中的点.
(2) 当 ab>0 时,点M 位于第几象限?
a<0,b<0 时,点M在第三象限.
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
典型例题
a<0,b<0 时,点 M 在第三象限;
a>0,b<0 时,点 M 在第四象限;
2.点 M(a,b) 为平面直角坐标系中的点.
(3) 当 a 为任意实数,且 b<0 时,点 M 位于第几象限?
a=0,b<0 时,点 M 在 y 轴的负半轴.
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
x
y
巩固新知
练习1
随堂练习
写出图中点 A,B,C,D,E,F 的坐标.
E
C
A
F
B
D
A(–2,–2)
B(–5,4)
C(5,–4)
D(0,–3)
E(2,5)
F(–4,0)
创设情境
探究新知
课堂小结
布置作业
应用新知
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
x
y
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
在图中描出下列各点:
L
L(–5,–3) ,M(4,0) ,N(–6,2) ,P(5,–3.5) ,Q(0,5) ,R(6,2) .
M
N
P
Q
R
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
(1) 下列各点中,在第二象限的是( )
A.(2,3) B.(2,–3)
C.(–2,–3) D.(– 2,3)
(2) 下列各点中,在 x 轴上的点是( )
A.(0,3) B.(–3,0)
C.(–1,2) D.(–2,–3)
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
D
B
x轴上的点:纵坐标都是 0;
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习4
随堂练习
(1) 若 |a| = 5,|b| = 4,且点 M(a,b) 在第二象限,则点 M 的
坐标是 .
(–5,4)
(2) 已知坐标平面内点 A(a,b) 在第四象限,那么点 B(b,a)
在第 象限,点 C(–a,–b) 在第 象限.
二
二
分析:由点 M 在第二象限得,a<0,b>0.又知道 |a| = 5,|b| = 4,所以 a = –5,b = 4.
分析:由点 A 在第四象限得,a>0,b<0,所以 –a<0,–b>0.所以点B(b,a) 在第二象限,点C(–a,–b) 也在第二象限.
平面直角坐标系
相关概念:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向;两坐标轴的交点为平面直角坐标系的原点.坐标平面被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四部分,每个部分称为象限,分别叫第一象限、第二象限、第三象限、第四象限.
点的坐标特点:
原点坐标为(0,0) ,
x 轴上的点纵坐标为0,
y 轴上的点横坐标为0,
坐标轴上的点不在任何象限内.
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
课堂小结
创设情境
探究新知
应用新知
巩固新知
布置作业
布置作业
教科书第68页练习7.1
第3、4题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
7.1.2 平面直角坐标系
学习目标
平面直角坐标系
1.理解平面直角坐标系的相关概念.
2.掌握平面直角坐标系内点与坐标是一一对应的.
3.理解在平面直角坐标系中四个象限的点对应坐标的符号特征.
4.能运用点的坐标的符号特征解决问题,进一步体会数形结合思想的作用.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
什么是数轴?请你试着画出一条数轴.
–5 –4 –3 –2 –1 0 1 2 3 4 5
回顾
追问:A,B 两点所表示的数分别是什么?
A
B
·
·
A 点表示 – 4,B 点表示 2.
描一描:请你在上边的数轴上标出“–5”表示的点.
·
–5 –4 –3 –2 –1 0 1 2 3 4 5
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
A
B
·
·
数轴上的点与坐标有怎样的关系?
“一一对应”的
思考
类似于利用数轴确定直线上点的位置,结合学习的有序数对知识,能不能找到一种办法来确定平面内点的位置?
B
A
D
C
横
排
纵列
4
3
2
1
3
2
4
1
点 A 在“第3列第4排”
记为(3,4)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
类似于利用数轴确定直线上点的位置,结合学习的有序数对知识,能不能找到一种办法来确定平面内点的位置?
A
B
D
C
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
4
3
2
1
5
–4
x 轴
x
y 轴
y
原点
A 点在 x 轴上对应 3,
A(3,4)
B(–3,–4)
C(0,2)
D(0, –3)
P
P(4,0)
A 点在 y 轴上对应 4.
x
y
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
类似于利用数轴确定直线上点的位置,结合学习的有序数对知识,能不能找到一种办法来确定平面内点的位置?
A
B
D
C
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
4
3
2
1
5
–4
x
y
(3,4)
(–3,–4)
(0,2)
(0, –3)
P
(4,0)
平面直角坐标系内任意一点的
坐标(x,y)的确定方法
从此点向x轴画垂线,垂足(垂线与x轴的交点)即是该点的横坐标(x);
从此点向y轴画垂线,垂足(垂线与y轴的交点)即是该点的纵坐标(y).
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
点 O 的坐标是什么?x 轴和 y 轴上的点的坐标有什么特点?
A
B
D
C
x
y
A(3,4)
B(–3,–4)
C(0,2)
D(0, –3)
原点O :
y 轴:
横坐标为0,
一般记为(0,y) ;
x 轴:
纵坐标为0,
一般记为(x,0) ;
C(0,2)
P(4,0)
P(4,0)
P
(0,0)
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
x
y
观察
x 轴
y 轴
原点
第一象限
Ⅰ
第二象限
Ⅱ
第三象限
Ⅲ
第四象限
Ⅳ
观察平面直角坐标系,学习其各部分的名称和对应点的特点.
P
原点的坐标是:O(0,0)
x轴上的点:纵坐标都是 0
y轴上的点:横坐标都是 0
四个象限内点的特点:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
注意:坐标轴上的点不属于任何象限.
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
观察与思考
在平面直角坐标系中描出下列各点:
y
A
B
C
D
E
平面上的点和坐标有什么关系呢?
平面上的点和坐标是一一对应的.
x
A(4,4),
B(–3,3),
C(–4,–2),
D(3.5,–2),
E(0,–3).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
如图,正方形 ABCD 的边长为 6,如果以点 A 为原点,AB 所在直线为 x 轴,建立平面直角坐标系,那么 y 轴是哪条线?
探究
x
C
B
A
D
请你写出正方形的顶点 A,B,C,D 的坐标.
A(0,0)
B(6,0)
C(6,6)
D(0,6)
试着再建立一个平面直角坐标系,这时正方形的顶点 A,B,C,D 的坐标又分别是什么?
y
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
1.在平面直角坐标系中描出下列各点:
A(4,5) ,B(–2,3) ,C(–4,–1) ,D(2.5,–2) ,E(0,–4) .
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
A
B
C
D
E
x
y
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
2.点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a>0,b<0 时,点 M 位于第几象限?
(2) 当 ab>0 时,点M 位于第几象限?
(3) 当 a 为任意实数,且 b<0 时,点 M 位于第几象限?
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
2.点 M(a,b) 为平面直角坐标系中的点.
(1) 当 a>0,b<0 时,点 M 位于第几象限?
第四象限
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
a>0,b>0 时,点M在第一象限;
2.点 M(a,b) 为平面直角坐标系中的点.
(2) 当 ab>0 时,点M 位于第几象限?
a<0,b<0 时,点M在第三象限.
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
典型例题
a<0,b<0 时,点 M 在第三象限;
a>0,b<0 时,点 M 在第四象限;
2.点 M(a,b) 为平面直角坐标系中的点.
(3) 当 a 为任意实数,且 b<0 时,点 M 位于第几象限?
a=0,b<0 时,点 M 在 y 轴的负半轴.
解析:在平面直角坐标系内,点的坐标特点为:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
原点的坐标是(0,0) ;
x轴上的点:纵坐标都是 0;
y轴上的点:横坐标都是 0;
坐标轴上的点不属于任何象限.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
x
y
巩固新知
练习1
随堂练习
写出图中点 A,B,C,D,E,F 的坐标.
E
C
A
F
B
D
A(–2,–2)
B(–5,4)
C(5,–4)
D(0,–3)
E(2,5)
F(–4,0)
创设情境
探究新知
课堂小结
布置作业
应用新知
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
x
y
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
在图中描出下列各点:
L
L(–5,–3) ,M(4,0) ,N(–6,2) ,P(5,–3.5) ,Q(0,5) ,R(6,2) .
M
N
P
Q
R
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
(1) 下列各点中,在第二象限的是( )
A.(2,3) B.(2,–3)
C.(–2,–3) D.(– 2,3)
(2) 下列各点中,在 x 轴上的点是( )
A.(0,3) B.(–3,0)
C.(–1,2) D.(–2,–3)
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
D
B
x轴上的点:纵坐标都是 0;
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习4
随堂练习
(1) 若 |a| = 5,|b| = 4,且点 M(a,b) 在第二象限,则点 M 的
坐标是 .
(–5,4)
(2) 已知坐标平面内点 A(a,b) 在第四象限,那么点 B(b,a)
在第 象限,点 C(–a,–b) 在第 象限.
二
二
分析:由点 M 在第二象限得,a<0,b>0.又知道 |a| = 5,|b| = 4,所以 a = –5,b = 4.
分析:由点 A 在第四象限得,a>0,b<0,所以 –a<0,–b>0.所以点B(b,a) 在第二象限,点C(–a,–b) 也在第二象限.
平面直角坐标系
相关概念:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向;两坐标轴的交点为平面直角坐标系的原点.坐标平面被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四部分,每个部分称为象限,分别叫第一象限、第二象限、第三象限、第四象限.
点的坐标特点:
原点坐标为(0,0) ,
x 轴上的点纵坐标为0,
y 轴上的点横坐标为0,
坐标轴上的点不在任何象限内.
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
课堂小结
创设情境
探究新知
应用新知
巩固新知
布置作业
布置作业
教科书第68页练习7.1
第3、4题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
