7.3.2.3正切函数的图象与性质 讲义(含解析)
文档属性
| 名称 | 7.3.2.3正切函数的图象与性质 讲义(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 870.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 15:56:37 | ||
图片预览




文档简介
编号:048 课题: §7.3.2.3 正切函数的图象与性质
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握正切函数的图象与性质;
2.会求正切函数的定义域、周期性、奇偶性;
3.掌握正切函数的单调性及应用;
4.理解并掌握正切函数图象、性质的综合应用.
本节重点难点
重点:正切函数的单调性及应用;
难点:正切函数图象、性质的综合应用.
学科素养目标
三角函数的基础是几何中的相似形和圆,而研究方法又主要是代数的,因此三角函数集中地体现了形数结合的思想,在代数和几何之间建立了初步的联系.在本章中,充分渗透了数形结合的思想.一方面是以形助数,突出了几何直观对理解抽象数学概念的作用.如在三角函数及其性质的学习中,注意充分发挥单位圆的直观作用,借助单位圆认识任意角、任意角的三角函数,理解三角函数的周期性、诱导公式、同角三角函数关系式以及三角函数的图象;通过角终边之间的对称关系来研究诱导公式;借助三角函数的图象理解三角函数在一个周期上的单调性、最大和最小值、图象与轴的交点等性质;另一方面以数助形.特别值得一提的是诱导公式的推导.首先提出问题:“由三角函数的定义可以知道:终边相同的角的同一三角函数值相等.
教学过程赏析
基础知识积累
正切函数的图象与性质
(1)图象与性质
解析式 y=tan x
图象
定义域
值域 R
周期 π
奇偶性 __________函数
对称 中心 _____________,k∈Z
单调性 在每一个区间___________________________ 上都单调递增
(2)本质:根据正切函数的解析式、图象,总结正切函数的性质.
(3)应用:画正切函数的图象,解决关于正切函数的定义域、值域、单调性等问题.
【思考】
正切函数在整个定义域上都是增函数吗
【课前基础演练】
题1.函数f(x)=lg 的定义域为( )
A.
B.
C.
D.
题2.当x∈ 时,函数y=tan |x|的图象( )
A.关于原点对称
B.关于y轴对称
C.关于x轴对称
D.无法确定
题3.已知函数f(x)=tan ωx在上单调递减,则ω的取值范围是( )
A.0<ω≤1 B.-1≤ω<0
C.-2≤ω<0 D.0<ω≤
题4.函数f(x)=tan 的最小正周期、对称中心分别是( )
A.
B.
C.
D.
题5.已知θ是三角形的一个内角,且tan θ≥-1,则θ的取值范围是( )
A.
B.
C.
D.以上都不对
题6.下列关于函数y=tan 的说法正确的是( )
A.在区间 上单调递增
B.最小正周期是π
C.图象关于点 对称
D.图象关于直线x= 对称
题7(多选题).下列各式中正确的是( )
A.tan 735°<tan 800°
B.tan 1>tan 2
C.tan <tan
D.tan <tan
题8(多选题).下列函数中是偶函数,且最小正周期为π的函数为( )
A.y=sin |x| B.y=
C.y= D.y=
题9.函数y=的定义域是________.
题10.函数y=2tan ωx(常数ω>0)在开区间 上是严格增函数,则实数ω的取值范围是________.
题11.求函数y=tan 的定义域、周期及单调区间.
【课堂检测达标】
题12. 函数的定义域为( )
A.
B.
C.
D.
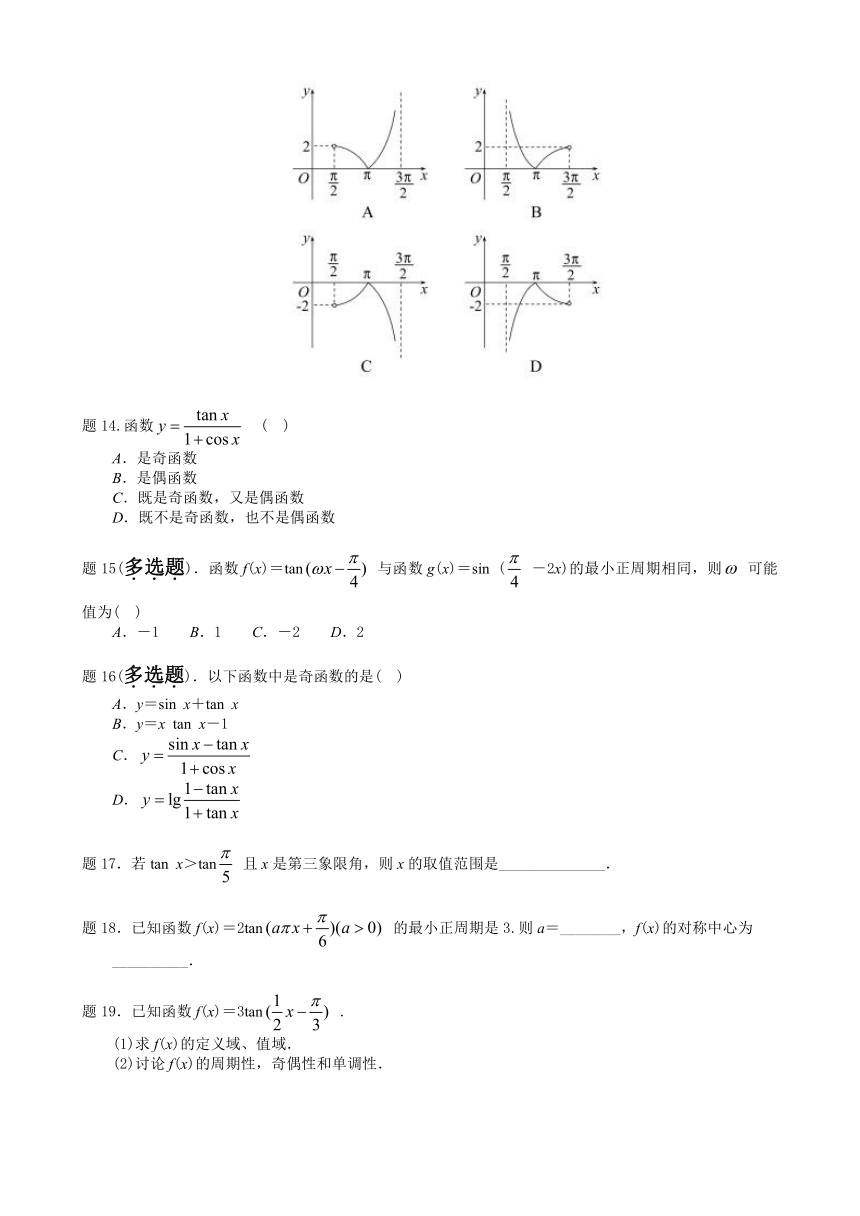
题13.函数y=tan x+sin x+ 在区间 内的图象是( )
题14.函数 ( )
A.是奇函数
B.是偶函数
C.既是奇函数,又是偶函数
D.既不是奇函数,也不是偶函数
题15(多选题).函数f(x)=tan 与函数g(x)=sin ( -2x)的最小正周期相同,则 可能值为( )
A.-1 B.1 C.-2 D.2
题16(多选题).以下函数中是奇函数的是( )
A.y=sin x+tan x
B.y=x tan x-1
C.
D.
题17.若tan x>tan 且x是第三象限角,则x的取值范围是______________.
题18.已知函数f(x)=2tan 的最小正周期是3.则a=________,f(x)的对称中心为
__________.
题19.已知函数f(x)=3tan .
(1)求f(x)的定义域、值域.
(2)讨论f(x)的周期性,奇偶性和单调性.
题20.是否存在整数a,使得函数y=tan ( -ax)在x∈ 上是单调递增的?若存在,求出a的值;若不存在,请说明理由.
【综合突破拔高】
题21.函数y=tan 的最小正周期是( )
A.4 B.4π C.2π D.2
题22.若函数y=3tan 的最小正周期是 ,则ω=( )
A.2 B.-2 C. D.±2
题23.函数f(x)=tan +tan是( )
A.奇函数 B.偶函数 C.既奇又偶函数 D.非奇非偶函数
题24.函数y=2tan图象的一个对称中心是( )
A. B. C. D.
题25.函数f(x)=x·tan x(-1≤x≤1)的图象可能是( )
题26.a=tan ,b=sin ,c=tan ,实数a,b,c的大小关系为( )
A.b题27(多选题).下列各式不成立的是( )
A.tan >tan
B.tan <tan
C.tan <tan
D.tan >tan
题28(多选题).关于函数f(x)=|tan x|的性质,下列叙述正确的是( )
A.f(x)的最小正周期为
B.f(x)是偶函数
C.f(x)的图象关于直线 对称
D.f(x)在每一个区间 内单调递增
题29.①函数y=tan x在它的定义域内是增函数;②若α,β是第一象限角,且α>β,则tan α>tan β;③函数y=A sin (ωx+φ)一定是奇函数;④函数的最小正周期为 .上列四个命题中,正确的命题是________.
题30.函数y=tan ,x∈ 的值域是__________.
题31.求函数y=tan的定义域、周期及单调区间.
题32.(1)求函数y=tan 的单调区间;
(2)比较tan 与tan 的大小.
编号:048 课题: §7.3.2.3 正切函数的图象与性质
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握正切函数的图象与性质;
2.会求正切函数的定义域、周期性、奇偶性;
3.掌握正切函数的单调性及应用;
4.理解并掌握正切函数图象、性质的综合应用.
本节重点难点
重点:正切函数的单调性及应用;
难点:正切函数图象、性质的综合应用.
学科素养目标
三角函数的基础是几何中的相似形和圆,而研究方法又主要是代数的,因此三角函数集中地体现了形数结合的思想,在代数和几何之间建立了初步的联系.在本章中,充分渗透了数形结合的思想.一方面是以形助数,突出了几何直观对理解抽象数学概念的作用.如在三角函数及其性质的学习中,注意充分发挥单位圆的直观作用,借助单位圆认识任意角、任意角的三角函数,理解三角函数的周期性、诱导公式、同角三角函数关系式以及三角函数的图象;通过角终边之间的对称关系来研究诱导公式;借助三角函数的图象理解三角函数在一个周期上的单调性、最大和最小值、图象与轴的交点等性质;另一方面以数助形.特别值得一提的是诱导公式的推导.首先提出问题:“由三角函数的定义可以知道:终边相同的角的同一三角函数值相等.
教学过程赏析
基础知识积累
正切函数的图象与性质
(1)图象与性质
解析式 y=tan x
图象
定义域
值域 R
周期 π
奇偶性 _奇__函数
对称 中心 ____ ____,k∈Z
单调性 在每一个区间_____________ 上都单调递增
(2)本质:根据正切函数的解析式、图象,总结正切函数的性质.
(3)应用:画正切函数的图象,解决关于正切函数的定义域、值域、单调性等问题.
【思考】
正切函数在整个定义域上都是增函数吗
提示:不是.正切函数在每一个区间上是单调递增的.但在整个定义域上不是增函数.
【课前基础演练】
题1.函数f(x)=lg 的定义域为( )
A.
B.
C.
D.
【解析】选D.若函数有意义,则tan x-1>0,所以tan x>1,
所以kπ+题2.当x∈ 时,函数y=tan |x|的图象( )
A.关于原点对称
B.关于y轴对称
C.关于x轴对称
D.无法确定
【解析】选B.函数y=tan |x|,x∈是偶函数,其图象关于y轴对称.
题3.已知函数f(x)=tan ωx在上单调递减,则ω的取值范围是( )
A.0<ω≤1 B.-1≤ω<0
C.-2≤ω<0 D.0<ω≤
【解析】选B.由f(x)在上单调递减知:ω<0,且 ,因此- ,解得-1≤ω<0.
题4.函数f(x)=tan 的最小正周期、对称中心分别是( )
A.
B.
C.
D.
【解析】选D.因为ω= ,所以最小正周期T=.令 ,得,
所以f(x)的对称中心是.
题5.已知θ是三角形的一个内角,且tan θ≥-1,则θ的取值范围是( )
A.
B.
C.
D.以上都不对
【解析】选C.作出正切函数y=tan x(x∈(0,π))的图象,由图象可得tan θ≥-1的解集为
题6.下列关于函数y=tan 的说法正确的是( )
A.在区间 上单调递增
B.最小正周期是π
C.图象关于点 对称
D.图象关于直线x= 对称
【解析】选B.令kπ-题7(多选题).下列各式中正确的是( )
A.tan 735°<tan 800°
B.tan 1>tan 2
C.tan <tan
D.tan <tan
【解析】选ABD.因为tan 735°=tan (735°-720°)=tan 15°,tan 800°=tan (800°-720°)=tan 80°且0°<15°<80°<90°,正切函数在 上单调递增,
所以tan 735°<tan 800°;tan 1>tan 0=0,tan 2<0,所以tan 1>tan 2;
因为 ,且正切函数在 上是单调递增的,所以tan >tan,
因为tan=tan,且 ,正切函数在2 (π)上单调递增,所以tan<tan,
即tan题8(多选题).下列函数中是偶函数,且最小正周期为π的函数为( )
A.y=sin |x| B.y=
C.y= D.y=
【解析】选BC.A的图象如下,
根据图象可知,图象关于y轴对称,y=sin |x|是偶函数,但不是周期函数,所以排除A;
B的图象如下,
根据图象可知,图象关于y轴对称,y= 是偶函数,
最小正周期是π,所以B正确.C的图象如下,
根据图象可知,图象关于y轴对称,y= 是偶函数,最小正周期为π,所以C正确;
D的图象如下,
根据图象可知,图象关于y轴对称,y= 是偶函数,最小正周期为2π,所以排除D.
题9.函数y=的定义域是________.
【解析】由题意得1-tan x≥0即tan x≤1结合图象可解得kπ-答案: (k∈Z)
题10.函数y=2tan ωx(常数ω>0)在开区间 上是严格增函数,则实数ω的取值范围是________.
【解析】由题意可知,函数y=2tan ωx的单调递增区间为 ,
因函数y=2tan ωx(常数ω>0)在开区间上是严格增函数,
所以,解得ω∈ .
答案:
题11.求函数y=tan 的定义域、周期及单调区间.
【解析】由,得,所以函数y=tan的定义域为.T= =2π,所以函数y=tan的周期为2π.由,得.
所以函数y=tan的单调递增区间为.
【课堂检测达标】
题12. 函数的定义域为( )
A.
B.
C.
D.
【解析】选B.由题可得tan x+1≥0,即tan x≥-1,解得.
题13.函数y=tan x+sin x+ 在区间 内的图象是( )
【解析】选A.函数y=tan x+sin x+
当x=时,sin x= ,tan x=- ,所以tan x0,故排除C,D选项,
当x= 时,sin x=- ,tan x= ,所以tan x>sin x,所以f(x)=2tan x=2 >2,故排除B选项.
题14.函数 ( )
A.是奇函数
B.是偶函数
C.既是奇函数,又是偶函数
D.既不是奇函数,也不是偶函数
【解析】选A.因为1+cos x≠0,即cos x≠-1,
得x≠2kπ+π,k∈Z.
又tan x中x≠kπ+ ,k∈Z,所以函数的定义域关于(0,0)对称.
令f(x)=,则f(-x)==-f(x),所以f(x)为奇函数.
题15(多选题).函数f(x)=tan 与函数g(x)=sin ( -2x)的最小正周期相同,则 可能值为( )
A.-1 B.1 C.-2 D.2
【解析】选AB.g(x)的最小正周期为π,则 =π,得ω=±1.
题16(多选题).以下函数中是奇函数的是( )
A.y=sin x+tan x
B.y=x tan x-1
C.
D.
【解析】选ACD.A中,f(-x)=sin (-x)+tan(-x)=-sin x-tan x=-(sin x+tan x)=-f(x),故函数y=sin x+tan x是奇函数;
B中,f(-x)=-x tan (-x)-1=x tan x-1=f(x),故f(x)为偶函数;
C中,,
故f(x)为奇函数;
D中,,f(x)也为奇函数.
题17.若tan x>tan 且x是第三象限角,则x的取值范围是______________.
【解析】因为tan x>tan =tan,又x为第三象限角,所以2kπ+ <x<2kπ+ ( ).
答案:
题18.已知函数f(x)=2tan 的最小正周期是3.则a=________,f(x)的对称中心为
__________.
【解析】函数f(x)=2tan的最小正周期是3,则3= ,得a= ,
所以函数f(x)=2tan,
由 ,得 ,
故对称中心为 .
答案:
题19.已知函数f(x)=3tan .
(1)求f(x)的定义域、值域.
(2)讨论f(x)的周期性,奇偶性和单调性.
【解析】(1)由 ,解得 .所以定义域为,值域为R.
(2)f(x)为周期函数,周期T= =2π.f(x)为非奇非偶函数.由 ,解得.
所以函数的单调递增区间为 .
题20.是否存在整数a,使得函数y=tan ( -ax)在x∈ 上是单调递增的?若存在,求出a的值;若不存在,请说明理由.
【解析】存在.因为y=tan θ在区间(kπ- ,kπ+ )( )上是单调递增的,所以a<0.又x∈ ,所以-ax∈ ,
所以 ,所以
解得 -5 (2)-5 (8k)≤a≤6-8k(k∈Z).
令k=0,得- ≤a≤6不符合题意,
令k=-1,得 ≤a≤14不符合题意,令k=1,
此时-2≤a≤-2,所以a=-2<0,
所以存在整数a=-2,满足题意.
【综合突破拔高】
题21.函数y=tan 的最小正周期是( )
A.4 B.4π C.2π D.2
【解析】选D.T=.
题22.若函数y=3tan 的最小正周期是 ,则ω=( )
A.2 B.-2 C. D.±2
【解析】选D.依题意有T= = ,所以|ω|=2,所以ω=±2.
题23.函数f(x)=tan +tan是( )
A.奇函数 B.偶函数 C.既奇又偶函数 D.非奇非偶函数
【解析】选A.函数定义域为{x|x≠kπ-4 (π)且x≠kπ+4 (π),k∈Z},关于原点对称,
又f(-x)=tan+tan=-tan (x+ )-tan=-f(x),
所以函数是奇函数.
题24.函数y=2tan图象的一个对称中心是( )
A. B. C. D.
【解析】选A. ,则,验证四个选项,可知选项A正确.
题25.函数f(x)=x·tan x(-1≤x≤1)的图象可能是( )
【解析】选B.由f(x)=x tan x(-1≤x≤1),则f(-x)=(- x)tan (- x)=x tan x,
所以f(x)=f(- x),即函数f(x)是偶函数,故排除A,C,
当00,排除D.
题26.a=tan ,b=sin ,c=tan ,实数a,b,c的大小关系为( )
A.b【解析】选A.a=tan,b=sin=sin=sin,c=tan=tan=tan,
因为y=tan x在 上单调递增,所以tan >tan即c>a,因为0sin=b,
综上,c>a>b即b题27(多选题).下列各式不成立的是( )
A.tan >tan
B.tan <tan
C.tan <tan
D.tan >tan
【解析】选ABC.tan =tan <tan ;
tan =tan <tan ;
tan =tan ,tan =tan ,
因为tan >tan ,所以tan >tan ;
tan =tan =tan =-tan ,
tan =tan =tan =-tan ,
又tan >tan ,所以tan <tan .
题28(多选题).关于函数f(x)=|tan x|的性质,下列叙述正确的是( )
A.f(x)的最小正周期为
B.f(x)是偶函数
C.f(x)的图象关于直线 对称
D.f(x)在每一个区间 内单调递增
【解析】选BCD.对于函数f(x)=|tan x|的性质,根据该函数的图象知,其最小正周期为π,A错误;
又f(-x)=|tan (-x)|=|tan x|=f(x),所以f(x)是定义域上的偶函数,B正确;
根据函数f(x)的图象知,f(x)的图象关于直线对称,C正确;
根据f(x)的图象知,f(x)在每一个区间内单调递增,D正确.
题29.①函数y=tan x在它的定义域内是增函数;②若α,β是第一象限角,且α>β,则tan α>tan β;③函数y=A sin (ωx+φ)一定是奇函数;④函数的最小正周期为 .上列四个命题中,正确的命题是________.
【解析】函数y=tan x的定义域为,
当x= 时,y=1;当x= 时,y=1,所以函数y=tan x在它的定义域内不是增函数,故①不正确;当α= ,β= 时,满足α,β是第一象限角,且α>β,但是tan =tan =1,故②不正确;当φ= 时,y=A sin (ωx+φ)=A sin=A cos (ωx)为偶函数,故③不正确;
因为y=cos 的最小正周期为T= =π,而函数的图象是由函数y=cos的图象保留x轴上方的图象,将x轴下方的图象沿x轴翻折到x轴上方而得到的,所以函数的最小正周期是函数的最小正周期的一半,即函数的最小正周期是 ,故④正确.
答案:④
题30.函数y=tan ,x∈ 的值域是__________.
【解析】因为,所以 ,
所以tan <1,即函数的值域为(-∞,1).
答案:(-∞,1)
题31.求函数y=tan的定义域、周期及单调区间.
【解析】自变量x的取值应满足: ;即 ,
所以函数的定义 .
设,又tan (z+π)=tan z,
所以tan =tan 即,因为 ,
都有,所以函数的周期为2.
由 ,解得 ,
因此函数在区间 上单调递增.
题32.(1)求函数y=tan 的单调区间;
(2)比较tan 与tan 的大小.
【解析】(1)由 得,,
所以函数y=tan的单调递增区间是 .
(2)由于tan=tan=tan=-tan,
tan=-tan=-tan,又 ,
而y=tan x在 上单调递增,所以tan-tan,即tan >tan.
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握正切函数的图象与性质;
2.会求正切函数的定义域、周期性、奇偶性;
3.掌握正切函数的单调性及应用;
4.理解并掌握正切函数图象、性质的综合应用.
本节重点难点
重点:正切函数的单调性及应用;
难点:正切函数图象、性质的综合应用.
学科素养目标
三角函数的基础是几何中的相似形和圆,而研究方法又主要是代数的,因此三角函数集中地体现了形数结合的思想,在代数和几何之间建立了初步的联系.在本章中,充分渗透了数形结合的思想.一方面是以形助数,突出了几何直观对理解抽象数学概念的作用.如在三角函数及其性质的学习中,注意充分发挥单位圆的直观作用,借助单位圆认识任意角、任意角的三角函数,理解三角函数的周期性、诱导公式、同角三角函数关系式以及三角函数的图象;通过角终边之间的对称关系来研究诱导公式;借助三角函数的图象理解三角函数在一个周期上的单调性、最大和最小值、图象与轴的交点等性质;另一方面以数助形.特别值得一提的是诱导公式的推导.首先提出问题:“由三角函数的定义可以知道:终边相同的角的同一三角函数值相等.
教学过程赏析
基础知识积累
正切函数的图象与性质
(1)图象与性质
解析式 y=tan x
图象
定义域
值域 R
周期 π
奇偶性 __________函数
对称 中心 _____________,k∈Z
单调性 在每一个区间___________________________ 上都单调递增
(2)本质:根据正切函数的解析式、图象,总结正切函数的性质.
(3)应用:画正切函数的图象,解决关于正切函数的定义域、值域、单调性等问题.
【思考】
正切函数在整个定义域上都是增函数吗
【课前基础演练】
题1.函数f(x)=lg 的定义域为( )
A.
B.
C.
D.
题2.当x∈ 时,函数y=tan |x|的图象( )
A.关于原点对称
B.关于y轴对称
C.关于x轴对称
D.无法确定
题3.已知函数f(x)=tan ωx在上单调递减,则ω的取值范围是( )
A.0<ω≤1 B.-1≤ω<0
C.-2≤ω<0 D.0<ω≤
题4.函数f(x)=tan 的最小正周期、对称中心分别是( )
A.
B.
C.
D.
题5.已知θ是三角形的一个内角,且tan θ≥-1,则θ的取值范围是( )
A.
B.
C.
D.以上都不对
题6.下列关于函数y=tan 的说法正确的是( )
A.在区间 上单调递增
B.最小正周期是π
C.图象关于点 对称
D.图象关于直线x= 对称
题7(多选题).下列各式中正确的是( )
A.tan 735°<tan 800°
B.tan 1>tan 2
C.tan <tan
D.tan <tan
题8(多选题).下列函数中是偶函数,且最小正周期为π的函数为( )
A.y=sin |x| B.y=
C.y= D.y=
题9.函数y=的定义域是________.
题10.函数y=2tan ωx(常数ω>0)在开区间 上是严格增函数,则实数ω的取值范围是________.
题11.求函数y=tan 的定义域、周期及单调区间.
【课堂检测达标】
题12. 函数的定义域为( )
A.
B.
C.
D.
题13.函数y=tan x+sin x+ 在区间 内的图象是( )
题14.函数 ( )
A.是奇函数
B.是偶函数
C.既是奇函数,又是偶函数
D.既不是奇函数,也不是偶函数
题15(多选题).函数f(x)=tan 与函数g(x)=sin ( -2x)的最小正周期相同,则 可能值为( )
A.-1 B.1 C.-2 D.2
题16(多选题).以下函数中是奇函数的是( )
A.y=sin x+tan x
B.y=x tan x-1
C.
D.
题17.若tan x>tan 且x是第三象限角,则x的取值范围是______________.
题18.已知函数f(x)=2tan 的最小正周期是3.则a=________,f(x)的对称中心为
__________.
题19.已知函数f(x)=3tan .
(1)求f(x)的定义域、值域.
(2)讨论f(x)的周期性,奇偶性和单调性.
题20.是否存在整数a,使得函数y=tan ( -ax)在x∈ 上是单调递增的?若存在,求出a的值;若不存在,请说明理由.
【综合突破拔高】
题21.函数y=tan 的最小正周期是( )
A.4 B.4π C.2π D.2
题22.若函数y=3tan 的最小正周期是 ,则ω=( )
A.2 B.-2 C. D.±2
题23.函数f(x)=tan +tan是( )
A.奇函数 B.偶函数 C.既奇又偶函数 D.非奇非偶函数
题24.函数y=2tan图象的一个对称中心是( )
A. B. C. D.
题25.函数f(x)=x·tan x(-1≤x≤1)的图象可能是( )
题26.a=tan ,b=sin ,c=tan ,实数a,b,c的大小关系为( )
A.b
A.tan >tan
B.tan <tan
C.tan <tan
D.tan >tan
题28(多选题).关于函数f(x)=|tan x|的性质,下列叙述正确的是( )
A.f(x)的最小正周期为
B.f(x)是偶函数
C.f(x)的图象关于直线 对称
D.f(x)在每一个区间 内单调递增
题29.①函数y=tan x在它的定义域内是增函数;②若α,β是第一象限角,且α>β,则tan α>tan β;③函数y=A sin (ωx+φ)一定是奇函数;④函数的最小正周期为 .上列四个命题中,正确的命题是________.
题30.函数y=tan ,x∈ 的值域是__________.
题31.求函数y=tan的定义域、周期及单调区间.
题32.(1)求函数y=tan 的单调区间;
(2)比较tan 与tan 的大小.
编号:048 课题: §7.3.2.3 正切函数的图象与性质
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1.理解并掌握正切函数的图象与性质;
2.会求正切函数的定义域、周期性、奇偶性;
3.掌握正切函数的单调性及应用;
4.理解并掌握正切函数图象、性质的综合应用.
本节重点难点
重点:正切函数的单调性及应用;
难点:正切函数图象、性质的综合应用.
学科素养目标
三角函数的基础是几何中的相似形和圆,而研究方法又主要是代数的,因此三角函数集中地体现了形数结合的思想,在代数和几何之间建立了初步的联系.在本章中,充分渗透了数形结合的思想.一方面是以形助数,突出了几何直观对理解抽象数学概念的作用.如在三角函数及其性质的学习中,注意充分发挥单位圆的直观作用,借助单位圆认识任意角、任意角的三角函数,理解三角函数的周期性、诱导公式、同角三角函数关系式以及三角函数的图象;通过角终边之间的对称关系来研究诱导公式;借助三角函数的图象理解三角函数在一个周期上的单调性、最大和最小值、图象与轴的交点等性质;另一方面以数助形.特别值得一提的是诱导公式的推导.首先提出问题:“由三角函数的定义可以知道:终边相同的角的同一三角函数值相等.
教学过程赏析
基础知识积累
正切函数的图象与性质
(1)图象与性质
解析式 y=tan x
图象
定义域
值域 R
周期 π
奇偶性 _奇__函数
对称 中心 ____ ____,k∈Z
单调性 在每一个区间_____________ 上都单调递增
(2)本质:根据正切函数的解析式、图象,总结正切函数的性质.
(3)应用:画正切函数的图象,解决关于正切函数的定义域、值域、单调性等问题.
【思考】
正切函数在整个定义域上都是增函数吗
提示:不是.正切函数在每一个区间上是单调递增的.但在整个定义域上不是增函数.
【课前基础演练】
题1.函数f(x)=lg 的定义域为( )
A.
B.
C.
D.
【解析】选D.若函数有意义,则tan x-1>0,所以tan x>1,
所以kπ+
A.关于原点对称
B.关于y轴对称
C.关于x轴对称
D.无法确定
【解析】选B.函数y=tan |x|,x∈是偶函数,其图象关于y轴对称.
题3.已知函数f(x)=tan ωx在上单调递减,则ω的取值范围是( )
A.0<ω≤1 B.-1≤ω<0
C.-2≤ω<0 D.0<ω≤
【解析】选B.由f(x)在上单调递减知:ω<0,且 ,因此- ,解得-1≤ω<0.
题4.函数f(x)=tan 的最小正周期、对称中心分别是( )
A.
B.
C.
D.
【解析】选D.因为ω= ,所以最小正周期T=.令 ,得,
所以f(x)的对称中心是.
题5.已知θ是三角形的一个内角,且tan θ≥-1,则θ的取值范围是( )
A.
B.
C.
D.以上都不对
【解析】选C.作出正切函数y=tan x(x∈(0,π))的图象,由图象可得tan θ≥-1的解集为
题6.下列关于函数y=tan 的说法正确的是( )
A.在区间 上单调递增
B.最小正周期是π
C.图象关于点 对称
D.图象关于直线x= 对称
【解析】选B.令kπ-
A.tan 735°<tan 800°
B.tan 1>tan 2
C.tan <tan
D.tan <tan
【解析】选ABD.因为tan 735°=tan (735°-720°)=tan 15°,tan 800°=tan (800°-720°)=tan 80°且0°<15°<80°<90°,正切函数在 上单调递增,
所以tan 735°<tan 800°;tan 1>tan 0=0,tan 2<0,所以tan 1>tan 2;
因为 ,且正切函数在 上是单调递增的,所以tan >tan,
因为tan=tan,且 ,正切函数在2 (π)上单调递增,所以tan<tan,
即tan
A.y=sin |x| B.y=
C.y= D.y=
【解析】选BC.A的图象如下,
根据图象可知,图象关于y轴对称,y=sin |x|是偶函数,但不是周期函数,所以排除A;
B的图象如下,
根据图象可知,图象关于y轴对称,y= 是偶函数,
最小正周期是π,所以B正确.C的图象如下,
根据图象可知,图象关于y轴对称,y= 是偶函数,最小正周期为π,所以C正确;
D的图象如下,
根据图象可知,图象关于y轴对称,y= 是偶函数,最小正周期为2π,所以排除D.
题9.函数y=的定义域是________.
【解析】由题意得1-tan x≥0即tan x≤1结合图象可解得kπ-
题10.函数y=2tan ωx(常数ω>0)在开区间 上是严格增函数,则实数ω的取值范围是________.
【解析】由题意可知,函数y=2tan ωx的单调递增区间为 ,
因函数y=2tan ωx(常数ω>0)在开区间上是严格增函数,
所以,解得ω∈ .
答案:
题11.求函数y=tan 的定义域、周期及单调区间.
【解析】由,得,所以函数y=tan的定义域为.T= =2π,所以函数y=tan的周期为2π.由,得.
所以函数y=tan的单调递增区间为.
【课堂检测达标】
题12. 函数的定义域为( )
A.
B.
C.
D.
【解析】选B.由题可得tan x+1≥0,即tan x≥-1,解得.
题13.函数y=tan x+sin x+ 在区间 内的图象是( )
【解析】选A.函数y=tan x+sin x+
当x=时,sin x= ,tan x=- ,所以tan x
当x= 时,sin x=- ,tan x= ,所以tan x>sin x,所以f(x)=2tan x=2 >2,故排除B选项.
题14.函数 ( )
A.是奇函数
B.是偶函数
C.既是奇函数,又是偶函数
D.既不是奇函数,也不是偶函数
【解析】选A.因为1+cos x≠0,即cos x≠-1,
得x≠2kπ+π,k∈Z.
又tan x中x≠kπ+ ,k∈Z,所以函数的定义域关于(0,0)对称.
令f(x)=,则f(-x)==-f(x),所以f(x)为奇函数.
题15(多选题).函数f(x)=tan 与函数g(x)=sin ( -2x)的最小正周期相同,则 可能值为( )
A.-1 B.1 C.-2 D.2
【解析】选AB.g(x)的最小正周期为π,则 =π,得ω=±1.
题16(多选题).以下函数中是奇函数的是( )
A.y=sin x+tan x
B.y=x tan x-1
C.
D.
【解析】选ACD.A中,f(-x)=sin (-x)+tan(-x)=-sin x-tan x=-(sin x+tan x)=-f(x),故函数y=sin x+tan x是奇函数;
B中,f(-x)=-x tan (-x)-1=x tan x-1=f(x),故f(x)为偶函数;
C中,,
故f(x)为奇函数;
D中,,f(x)也为奇函数.
题17.若tan x>tan 且x是第三象限角,则x的取值范围是______________.
【解析】因为tan x>tan =tan,又x为第三象限角,所以2kπ+ <x<2kπ+ ( ).
答案:
题18.已知函数f(x)=2tan 的最小正周期是3.则a=________,f(x)的对称中心为
__________.
【解析】函数f(x)=2tan的最小正周期是3,则3= ,得a= ,
所以函数f(x)=2tan,
由 ,得 ,
故对称中心为 .
答案:
题19.已知函数f(x)=3tan .
(1)求f(x)的定义域、值域.
(2)讨论f(x)的周期性,奇偶性和单调性.
【解析】(1)由 ,解得 .所以定义域为,值域为R.
(2)f(x)为周期函数,周期T= =2π.f(x)为非奇非偶函数.由 ,解得.
所以函数的单调递增区间为 .
题20.是否存在整数a,使得函数y=tan ( -ax)在x∈ 上是单调递增的?若存在,求出a的值;若不存在,请说明理由.
【解析】存在.因为y=tan θ在区间(kπ- ,kπ+ )( )上是单调递增的,所以a<0.又x∈ ,所以-ax∈ ,
所以 ,所以
解得 -5 (2)-5 (8k)≤a≤6-8k(k∈Z).
令k=0,得- ≤a≤6不符合题意,
令k=-1,得 ≤a≤14不符合题意,令k=1,
此时-2≤a≤-2,所以a=-2<0,
所以存在整数a=-2,满足题意.
【综合突破拔高】
题21.函数y=tan 的最小正周期是( )
A.4 B.4π C.2π D.2
【解析】选D.T=.
题22.若函数y=3tan 的最小正周期是 ,则ω=( )
A.2 B.-2 C. D.±2
【解析】选D.依题意有T= = ,所以|ω|=2,所以ω=±2.
题23.函数f(x)=tan +tan是( )
A.奇函数 B.偶函数 C.既奇又偶函数 D.非奇非偶函数
【解析】选A.函数定义域为{x|x≠kπ-4 (π)且x≠kπ+4 (π),k∈Z},关于原点对称,
又f(-x)=tan+tan=-tan (x+ )-tan=-f(x),
所以函数是奇函数.
题24.函数y=2tan图象的一个对称中心是( )
A. B. C. D.
【解析】选A. ,则,验证四个选项,可知选项A正确.
题25.函数f(x)=x·tan x(-1≤x≤1)的图象可能是( )
【解析】选B.由f(x)=x tan x(-1≤x≤1),则f(-x)=(- x)tan (- x)=x tan x,
所以f(x)=f(- x),即函数f(x)是偶函数,故排除A,C,
当0
题26.a=tan ,b=sin ,c=tan ,实数a,b,c的大小关系为( )
A.b
因为y=tan x在 上单调递增,所以tan >tan即c>a,因为0
综上,c>a>b即b
A.tan >tan
B.tan <tan
C.tan <tan
D.tan >tan
【解析】选ABC.tan =tan <tan ;
tan =tan <tan ;
tan =tan ,tan =tan ,
因为tan >tan ,所以tan >tan ;
tan =tan =tan =-tan ,
tan =tan =tan =-tan ,
又tan >tan ,所以tan <tan .
题28(多选题).关于函数f(x)=|tan x|的性质,下列叙述正确的是( )
A.f(x)的最小正周期为
B.f(x)是偶函数
C.f(x)的图象关于直线 对称
D.f(x)在每一个区间 内单调递增
【解析】选BCD.对于函数f(x)=|tan x|的性质,根据该函数的图象知,其最小正周期为π,A错误;
又f(-x)=|tan (-x)|=|tan x|=f(x),所以f(x)是定义域上的偶函数,B正确;
根据函数f(x)的图象知,f(x)的图象关于直线对称,C正确;
根据f(x)的图象知,f(x)在每一个区间内单调递增,D正确.
题29.①函数y=tan x在它的定义域内是增函数;②若α,β是第一象限角,且α>β,则tan α>tan β;③函数y=A sin (ωx+φ)一定是奇函数;④函数的最小正周期为 .上列四个命题中,正确的命题是________.
【解析】函数y=tan x的定义域为,
当x= 时,y=1;当x= 时,y=1,所以函数y=tan x在它的定义域内不是增函数,故①不正确;当α= ,β= 时,满足α,β是第一象限角,且α>β,但是tan =tan =1,故②不正确;当φ= 时,y=A sin (ωx+φ)=A sin=A cos (ωx)为偶函数,故③不正确;
因为y=cos 的最小正周期为T= =π,而函数的图象是由函数y=cos的图象保留x轴上方的图象,将x轴下方的图象沿x轴翻折到x轴上方而得到的,所以函数的最小正周期是函数的最小正周期的一半,即函数的最小正周期是 ,故④正确.
答案:④
题30.函数y=tan ,x∈ 的值域是__________.
【解析】因为,所以 ,
所以tan <1,即函数的值域为(-∞,1).
答案:(-∞,1)
题31.求函数y=tan的定义域、周期及单调区间.
【解析】自变量x的取值应满足: ;即 ,
所以函数的定义 .
设,又tan (z+π)=tan z,
所以tan =tan 即,因为 ,
都有,所以函数的周期为2.
由 ,解得 ,
因此函数在区间 上单调递增.
题32.(1)求函数y=tan 的单调区间;
(2)比较tan 与tan 的大小.
【解析】(1)由 得,,
所以函数y=tan的单调递增区间是 .
(2)由于tan=tan=tan=-tan,
tan=-tan=-tan,又 ,
而y=tan x在 上单调递增,所以tan
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
