2023—2024学年人教版数学九年级上册22.3实际问题与二次函数 同步练习题 (含解析)
文档属性
| 名称 | 2023—2024学年人教版数学九年级上册22.3实际问题与二次函数 同步练习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 547.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 11:35:51 | ||
图片预览



文档简介
2023-2024学年人教版九年级数学上册《22.3实际问题与二次函数》同步练习题(附答案)
一、单选题
1.现有一根长为的铁丝,把它弯成一个矩形,设矩形的面积为,一边长为,则y与x之间的函数表达式为( )
A. B. C. D.
2.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是.小球运动到最高点所需的时间是( )
A.2s B.3s C.4s D.5s
3.利用长为的墙和长的篱笆来围成一个矩形苗圃园,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为( )
A., B.,
C., D.,
4.某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(万元)与销售量x(辆)之间分别满足:,,若该公司在甲、乙两地共销售15辆该品牌的汽车,则能获得的最大利润为( )
A.30万元 B.38万元 C.46万元 D.48万元
5.一座拱桥的轮廓是抛物线型(如图所示),桥高为8米,拱高6米,跨度20米.相邻两支柱间的距离均为5米,则支柱的高度为( )米.
A.米 B.3米 C.米 D.4米
6.如图是一款抛物线型落地灯筒示意图,防滑螺母为抛物线支架的最高点,灯罩距离地面米,最高点距灯柱的水平距离为米,灯柱为米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离为多少米.( )
A. B. C. D.
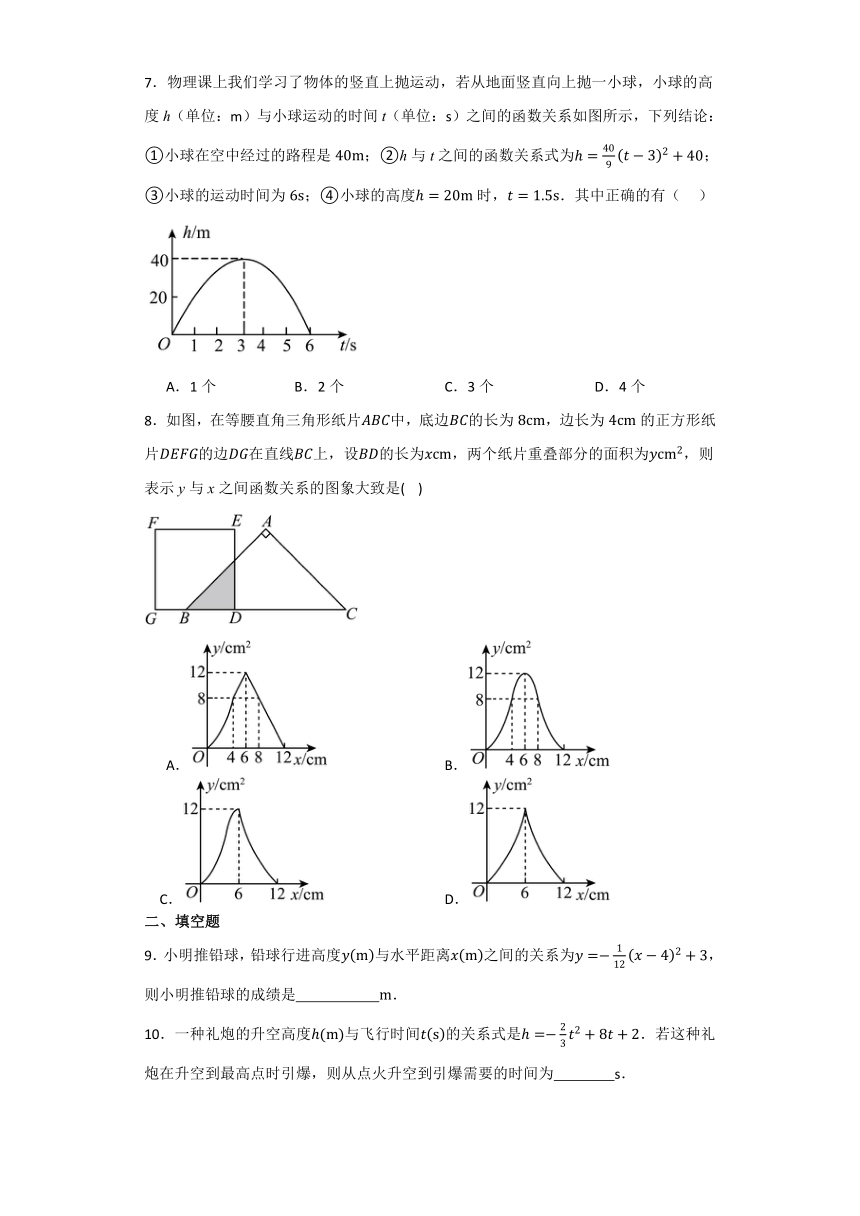
7.物理课上我们学习了物体的竖直上抛运动,若从地面竖直向上抛一小球,小球的高度h(单位:m)与小球运动的时间t(单位:s)之间的函数关系如图所示,下列结论:①小球在空中经过的路程是;②h与t之间的函数关系式为;③小球的运动时间为;④小球的高度时,.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在等腰直角三角形纸片中,底边的长为,边长为的正方形纸片的边在直线上,设的长为,两个纸片重叠部分的面积为,则表示y与x之间函数关系的图象大致是( )
B.
C. D.
二、填空题
9.小明推铅球,铅球行进高度与水平距离之间的关系为,则小明推铅球的成绩是 .
10.一种礼炮的升空高度与飞行时间的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为 s.
11.如图,王叔叔想用长为的栅栏,再借助房屋的外墙围成一个矩形羊圈,已知房屋外墙足够长,当矩形的边 时,羊圈的面积最大.
12.如图,P是抛物线在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形周长的最大值为 .
13.对于竖直向上抛出的物体,在不考虑空气阻力的情况下,有如下的关系式:,其中h是物体上升的高度,v是抛出时的速度,g是重力加速度(),t是抛出后的时间.如果一物体以的初速度从地面竖直向上抛出,经过 秒钟后它在离地面高的地方.
14.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径间,按相同间隔米用5根立柱加固,拱高为米,则立柱的长为 米.
15.如图,在矩形中,,,点P从点A出发,沿线段以每秒1个单位长度的速度向终点D运动;点Q从点B出发,沿线段以每秒2个单位长度的速度向终点A运动. P,Q两点同时出发,设点P运动的时间为(单位:秒),的面积为.则关于的函数表达式为 .
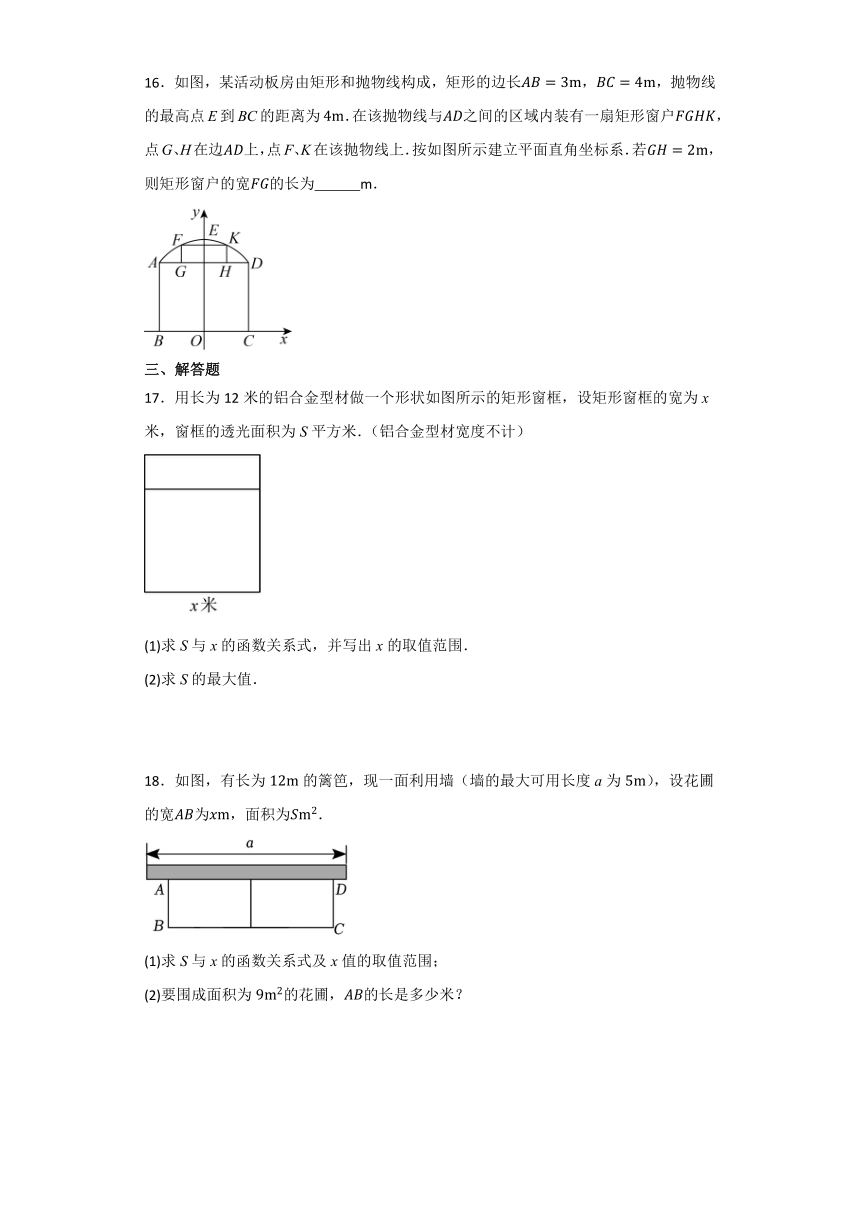
16.如图,某活动板房由矩形和抛物线构成,矩形的边长,,抛物线的最高点E到BC的距离为.在该抛物线与之间的区域内装有一扇矩形窗户,点G、H在边上,点F、K在该抛物线上.按如图所示建立平面直角坐标系.若,则矩形窗户的宽的长为 m.
三、解答题
17.用长为12米的铝合金型材做一个形状如图所示的矩形窗框,设矩形窗框的宽为x米,窗框的透光面积为S平方米.(铝合金型材宽度不计)
(1)求S与x的函数关系式,并写出x的取值范围.
(2)求S的最大值.
18.如图,有长为的篱笆,现一面利用墙(墙的最大可用长度a为),设花圃的宽为,面积为.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为的花圃,的长是多少米?
19.某超市购进一种每件价格为100元的新上衣,在超市试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系.
(1)求出y与x之间的函数关系式;
(2)如果超市销售这种上衣,每天要获得1200元利润,那么每件上衣的销售价应定为多少元?
(3)写出每天的利润W与销售单价x之间的函数关系式;若你是超市销售经理,会将销售价定为多少,来保证每天获得的利润最大,最大利润是多少?
20.年东京奥运会,中国跳水队赢得个项目中的块金牌,优异成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板长为米,跳板距水面的高为米,训练时跳水曲线在离起跳点水平距离米时达到距水面最大高度米,现以为横轴,为纵轴建立直角坐标系.
(1)时,求这条抛物线的解析式.
(2)(1)的条件下,求运动员落水点与点的距离.
(3)图中米,米,若跳水运动员在区域内(不含点)入水时才能达到训练要求,求的取值范围.
21.一座拱桥的示意图如图所示,当水面宽为米时,桥洞顶部离水面米.已知桥洞的拱桥是抛物线,请尝试解决以下问题:
(1)【问题1】建立合适的平面直角坐标系,求该抛物线的表达式.
(2)【问题2】由于暴雨导致水位上涨了米,求此时水面的宽度.
(3)【问题3】已知一艘货船的高为米,宽为米,其截面如图所示.为保证这艘货船可以安全通过拱桥,水面在正常水位的基础上最多能上升多少米?
参考答案
1.解:由题意得:矩形的另一边长,
∴,
故选:D.
2.解: ,
∵,
∴当时,有最大值,最大值为45.
故选:B.
3.解;设垂直于墙的一边长为,则平行于墙的一边长为,矩形面积为,
∵平行于墙的一边长不小于,墙的长度为
∴,
∴,
,
∵,
∴当时,y随x增大而减小,
∴当时,,
当时,,
∴这个苗圃园面积的最大值和最小值分别为,,
故选A.
4.解:设在甲地销售x辆,则在乙地销售辆,总利润为W万元,根据题意得出:
,
∴当时,取最大值,且最大值为46,
∴该公司在甲、乙两地共销售15辆该品牌的汽车,则能获得的最大利润为46万元,故C正确.
故选:C.
5.解:如图,设拱桥两端分别为点A、B,拱桥顶端为点C,以所在的直线为x轴,以的中点O为坐标原点,所在的直线为y轴建立平面直角坐标系,则点,点M,N的横坐标为5,
设抛物线的解析式为,
把点代入得:
,解得:,
∴抛物线的解析式为,
当时,,
∴支柱的高度为米.
故选:C
6.解:如图所示,以所在直线为轴、所在直线为轴建立平面直角坐标系,
根据题意知,抛物线的顶点的坐标为,
设抛物线的解析式为,
将点代入得,,
解得,
抛物线的解析式为,
当时,,
解得舍或,
所以茶几到灯柱的距离为米,
故选:A.
7.解:①由图象知小球在空中达到的最大高度是40m;
故①错误;
②设函数解析式为:,
把代入得,
解得,
函数解析式为,
故②错误;
③令,,
解得:或6,
小球的运动时间为,
故③正确;
④把代入解析式得,,
解得:或,
小球的高度时,为秒或秒,
故④错误;
综上,正确的只有一个,
故选:A.
8.解:当时,如下图所示:
是等腰直角三角形,四边形是正方形,
,,
是等腰直角三角形,
,
,即;
当时,如下图所示:
同理可证,是等腰直角三角形,
,
即;
当时,如下图所示:
,即;
综上所述,y与x的函数关系式为:
,
画出图象如下图所示:
故选B.
9.解:铅球落地时,高度,
令函数式中,即,
解得:(舍去),
即小强推铅球的成绩是.
故答案为:10.
10.解:由题意可得:,
∵
∴这个二次函数图象开口向下.
∴当时,升到最高点.
故答案为:6.
11.解:设为,面积为,
由题意可得:,
当时,取得最大值,
即时,羊圈的面积最大,
故答案为:.
12.解:设点P的坐标为,,
由题意可知:四边形的周长,
∴,
当时,C有最大值.
故答案为:.
13.解:由题意得:.
整理得,
解得.
∴1秒或4秒后,物体处在离抛出点高的地方.
故答案为:1或4.
14.解:如图,以点C为坐标系的原点,
设抛物线解析式为,
由题知,图像过,
代入得:,
∴,即.
∵F点横坐标为,
∴当时,,
∴米
故答案为:.
15.解:∵,,,
∴,
∵矩形中,,
∴
.
故答案为:.
16.解:由题意可知,、、,
设抛物线解析式为,
,解得:
抛物线解析式为,
点G、H在边上,且,
、,
四边形是矩形,
设,
点在抛物线上,
,
,
故答案为:.
17.(1)解:由窗框的宽为米,则长为米,
根据题意得:,
∵,
∴,
∴S与x的函数关系式为;
(2)解:由(1)得:
.
∴当时,S有最大值,最大值为6.
18.(1)解:由题可知,花圃的宽为x米,则为米,
,
∴S与x的函数关系式为:;
∵墙的最大可用长度a为,即,
∴,
∴,
即自变量的取值范围是;
(2)解:由题意,得,
整理,得,
解得:,,
∵,
∴不合题意,舍去,
∴的长为.
19.解:(1)设y与x之间的函数关系式为,
由所给函数图象可知:
解得.
故y与x的函数关系式为;
(2)根据题意,得:
整理,得:,
解得:或,
答:每件商品的销售价应定为120元或160元;
(3)∵,
∴
,
∴当时,,
∴售价定为每件140元时,每天最大利润1600元
20.(1)解:根据题意可得,抛物线的顶点坐标为,点,
∴设抛物线的解析式为,
把点代入得,,解得,,
∴抛物线的解析式为.
(2)解:抛物线的解析式为,运动员落水点在轴上,
∴令,则,解得,,,
∵抛物线的对称轴为,且运动员落水点在对称轴的右边,
∴,即运动员落水点在轴上,表示数量为的位置,且点为原点,
∴运动员落水点与点的距离为.
(3)解:根据题意,
∵跳板长为米,跳板距水面的高为米,训练时跳水曲线在离起跳点水平距离米时达到距水面最大高度米,是固定不变的,
∴设抛物线的解析式为,且过点,
∴,则,
∵米,米,
∴当时,,则,解得,;
当时,,则,解得,;
综上所述,.
21.解:(1)以的中点为平面直角坐标系的原点,所在线为轴,过点作的垂线为轴,建立的平面直角坐标系如下:
根据所建立的平面直角坐标系可知,点的坐标为,抛物线的顶点坐标为
因此设抛物线的函数表达式为,
将代入得:,
解得:,
则所求的抛物线的函数表达式为;
(2)由题意,令得,
解得:,
则水面上升1m后的水面宽度为:(米),
(3)由题意,当时,,
∵一艘货船的高为米,
∴水面在正常水位的基础上最多能上升(米).
一、单选题
1.现有一根长为的铁丝,把它弯成一个矩形,设矩形的面积为,一边长为,则y与x之间的函数表达式为( )
A. B. C. D.
2.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是.小球运动到最高点所需的时间是( )
A.2s B.3s C.4s D.5s
3.利用长为的墙和长的篱笆来围成一个矩形苗圃园,若平行于墙的一边长不小于,则这个苗圃园面积的最大值和最小值分别为( )
A., B.,
C., D.,
4.某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(万元)与销售量x(辆)之间分别满足:,,若该公司在甲、乙两地共销售15辆该品牌的汽车,则能获得的最大利润为( )
A.30万元 B.38万元 C.46万元 D.48万元
5.一座拱桥的轮廓是抛物线型(如图所示),桥高为8米,拱高6米,跨度20米.相邻两支柱间的距离均为5米,则支柱的高度为( )米.
A.米 B.3米 C.米 D.4米
6.如图是一款抛物线型落地灯筒示意图,防滑螺母为抛物线支架的最高点,灯罩距离地面米,最高点距灯柱的水平距离为米,灯柱为米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离为多少米.( )
A. B. C. D.
7.物理课上我们学习了物体的竖直上抛运动,若从地面竖直向上抛一小球,小球的高度h(单位:m)与小球运动的时间t(单位:s)之间的函数关系如图所示,下列结论:①小球在空中经过的路程是;②h与t之间的函数关系式为;③小球的运动时间为;④小球的高度时,.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.如图,在等腰直角三角形纸片中,底边的长为,边长为的正方形纸片的边在直线上,设的长为,两个纸片重叠部分的面积为,则表示y与x之间函数关系的图象大致是( )
B.
C. D.
二、填空题
9.小明推铅球,铅球行进高度与水平距离之间的关系为,则小明推铅球的成绩是 .
10.一种礼炮的升空高度与飞行时间的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为 s.
11.如图,王叔叔想用长为的栅栏,再借助房屋的外墙围成一个矩形羊圈,已知房屋外墙足够长,当矩形的边 时,羊圈的面积最大.
12.如图,P是抛物线在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形周长的最大值为 .
13.对于竖直向上抛出的物体,在不考虑空气阻力的情况下,有如下的关系式:,其中h是物体上升的高度,v是抛出时的速度,g是重力加速度(),t是抛出后的时间.如果一物体以的初速度从地面竖直向上抛出,经过 秒钟后它在离地面高的地方.
14.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径间,按相同间隔米用5根立柱加固,拱高为米,则立柱的长为 米.
15.如图,在矩形中,,,点P从点A出发,沿线段以每秒1个单位长度的速度向终点D运动;点Q从点B出发,沿线段以每秒2个单位长度的速度向终点A运动. P,Q两点同时出发,设点P运动的时间为(单位:秒),的面积为.则关于的函数表达式为 .
16.如图,某活动板房由矩形和抛物线构成,矩形的边长,,抛物线的最高点E到BC的距离为.在该抛物线与之间的区域内装有一扇矩形窗户,点G、H在边上,点F、K在该抛物线上.按如图所示建立平面直角坐标系.若,则矩形窗户的宽的长为 m.
三、解答题
17.用长为12米的铝合金型材做一个形状如图所示的矩形窗框,设矩形窗框的宽为x米,窗框的透光面积为S平方米.(铝合金型材宽度不计)
(1)求S与x的函数关系式,并写出x的取值范围.
(2)求S的最大值.
18.如图,有长为的篱笆,现一面利用墙(墙的最大可用长度a为),设花圃的宽为,面积为.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为的花圃,的长是多少米?
19.某超市购进一种每件价格为100元的新上衣,在超市试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系.
(1)求出y与x之间的函数关系式;
(2)如果超市销售这种上衣,每天要获得1200元利润,那么每件上衣的销售价应定为多少元?
(3)写出每天的利润W与销售单价x之间的函数关系式;若你是超市销售经理,会将销售价定为多少,来保证每天获得的利润最大,最大利润是多少?
20.年东京奥运会,中国跳水队赢得个项目中的块金牌,优异成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板长为米,跳板距水面的高为米,训练时跳水曲线在离起跳点水平距离米时达到距水面最大高度米,现以为横轴,为纵轴建立直角坐标系.
(1)时,求这条抛物线的解析式.
(2)(1)的条件下,求运动员落水点与点的距离.
(3)图中米,米,若跳水运动员在区域内(不含点)入水时才能达到训练要求,求的取值范围.
21.一座拱桥的示意图如图所示,当水面宽为米时,桥洞顶部离水面米.已知桥洞的拱桥是抛物线,请尝试解决以下问题:
(1)【问题1】建立合适的平面直角坐标系,求该抛物线的表达式.
(2)【问题2】由于暴雨导致水位上涨了米,求此时水面的宽度.
(3)【问题3】已知一艘货船的高为米,宽为米,其截面如图所示.为保证这艘货船可以安全通过拱桥,水面在正常水位的基础上最多能上升多少米?
参考答案
1.解:由题意得:矩形的另一边长,
∴,
故选:D.
2.解: ,
∵,
∴当时,有最大值,最大值为45.
故选:B.
3.解;设垂直于墙的一边长为,则平行于墙的一边长为,矩形面积为,
∵平行于墙的一边长不小于,墙的长度为
∴,
∴,
,
∵,
∴当时,y随x增大而减小,
∴当时,,
当时,,
∴这个苗圃园面积的最大值和最小值分别为,,
故选A.
4.解:设在甲地销售x辆,则在乙地销售辆,总利润为W万元,根据题意得出:
,
∴当时,取最大值,且最大值为46,
∴该公司在甲、乙两地共销售15辆该品牌的汽车,则能获得的最大利润为46万元,故C正确.
故选:C.
5.解:如图,设拱桥两端分别为点A、B,拱桥顶端为点C,以所在的直线为x轴,以的中点O为坐标原点,所在的直线为y轴建立平面直角坐标系,则点,点M,N的横坐标为5,
设抛物线的解析式为,
把点代入得:
,解得:,
∴抛物线的解析式为,
当时,,
∴支柱的高度为米.
故选:C
6.解:如图所示,以所在直线为轴、所在直线为轴建立平面直角坐标系,
根据题意知,抛物线的顶点的坐标为,
设抛物线的解析式为,
将点代入得,,
解得,
抛物线的解析式为,
当时,,
解得舍或,
所以茶几到灯柱的距离为米,
故选:A.
7.解:①由图象知小球在空中达到的最大高度是40m;
故①错误;
②设函数解析式为:,
把代入得,
解得,
函数解析式为,
故②错误;
③令,,
解得:或6,
小球的运动时间为,
故③正确;
④把代入解析式得,,
解得:或,
小球的高度时,为秒或秒,
故④错误;
综上,正确的只有一个,
故选:A.
8.解:当时,如下图所示:
是等腰直角三角形,四边形是正方形,
,,
是等腰直角三角形,
,
,即;
当时,如下图所示:
同理可证,是等腰直角三角形,
,
即;
当时,如下图所示:
,即;
综上所述,y与x的函数关系式为:
,
画出图象如下图所示:
故选B.
9.解:铅球落地时,高度,
令函数式中,即,
解得:(舍去),
即小强推铅球的成绩是.
故答案为:10.
10.解:由题意可得:,
∵
∴这个二次函数图象开口向下.
∴当时,升到最高点.
故答案为:6.
11.解:设为,面积为,
由题意可得:,
当时,取得最大值,
即时,羊圈的面积最大,
故答案为:.
12.解:设点P的坐标为,,
由题意可知:四边形的周长,
∴,
当时,C有最大值.
故答案为:.
13.解:由题意得:.
整理得,
解得.
∴1秒或4秒后,物体处在离抛出点高的地方.
故答案为:1或4.
14.解:如图,以点C为坐标系的原点,
设抛物线解析式为,
由题知,图像过,
代入得:,
∴,即.
∵F点横坐标为,
∴当时,,
∴米
故答案为:.
15.解:∵,,,
∴,
∵矩形中,,
∴
.
故答案为:.
16.解:由题意可知,、、,
设抛物线解析式为,
,解得:
抛物线解析式为,
点G、H在边上,且,
、,
四边形是矩形,
设,
点在抛物线上,
,
,
故答案为:.
17.(1)解:由窗框的宽为米,则长为米,
根据题意得:,
∵,
∴,
∴S与x的函数关系式为;
(2)解:由(1)得:
.
∴当时,S有最大值,最大值为6.
18.(1)解:由题可知,花圃的宽为x米,则为米,
,
∴S与x的函数关系式为:;
∵墙的最大可用长度a为,即,
∴,
∴,
即自变量的取值范围是;
(2)解:由题意,得,
整理,得,
解得:,,
∵,
∴不合题意,舍去,
∴的长为.
19.解:(1)设y与x之间的函数关系式为,
由所给函数图象可知:
解得.
故y与x的函数关系式为;
(2)根据题意,得:
整理,得:,
解得:或,
答:每件商品的销售价应定为120元或160元;
(3)∵,
∴
,
∴当时,,
∴售价定为每件140元时,每天最大利润1600元
20.(1)解:根据题意可得,抛物线的顶点坐标为,点,
∴设抛物线的解析式为,
把点代入得,,解得,,
∴抛物线的解析式为.
(2)解:抛物线的解析式为,运动员落水点在轴上,
∴令,则,解得,,,
∵抛物线的对称轴为,且运动员落水点在对称轴的右边,
∴,即运动员落水点在轴上,表示数量为的位置,且点为原点,
∴运动员落水点与点的距离为.
(3)解:根据题意,
∵跳板长为米,跳板距水面的高为米,训练时跳水曲线在离起跳点水平距离米时达到距水面最大高度米,是固定不变的,
∴设抛物线的解析式为,且过点,
∴,则,
∵米,米,
∴当时,,则,解得,;
当时,,则,解得,;
综上所述,.
21.解:(1)以的中点为平面直角坐标系的原点,所在线为轴,过点作的垂线为轴,建立的平面直角坐标系如下:
根据所建立的平面直角坐标系可知,点的坐标为,抛物线的顶点坐标为
因此设抛物线的函数表达式为,
将代入得:,
解得:,
则所求的抛物线的函数表达式为;
(2)由题意,令得,
解得:,
则水面上升1m后的水面宽度为:(米),
(3)由题意,当时,,
∵一艘货船的高为米,
∴水面在正常水位的基础上最多能上升(米).
同课章节目录
