6.2第2课时 指数函数的图象与性质 课件(共18张PPT)
文档属性
| 名称 | 6.2第2课时 指数函数的图象与性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 00:00:00 | ||
图片预览



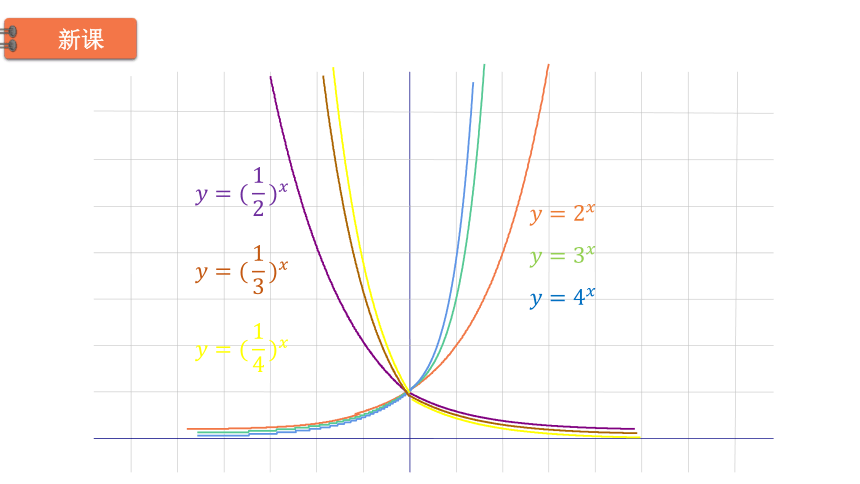

文档简介
(共18张PPT)
§6.2 第2课时 指数函数的图象与性质
第六章
【教学目标】
1.通过学生自主探究,让学生总结指数函数的图像与性质.
2.能掌握指数函数的图象和性质,会用指数函数的图象和性质解决相关的问题.
3.能应用指数函数及其性质解决实际应用题.
通过学习本节内容,培养学生的逻辑推理核心素养,提升学生的数学运算核心素养.
【核心素养】
复习回顾
注意
(1)底数:大于0且不等于1的常数
(2)指数:自变量x
(3)系数:1
指数函数的定义:
一般地,函数叫做指数函数,其中 是自变量, 函数的定义域是 .
图像
定义域
值域
奇偶性
定点
单调性
复习回顾
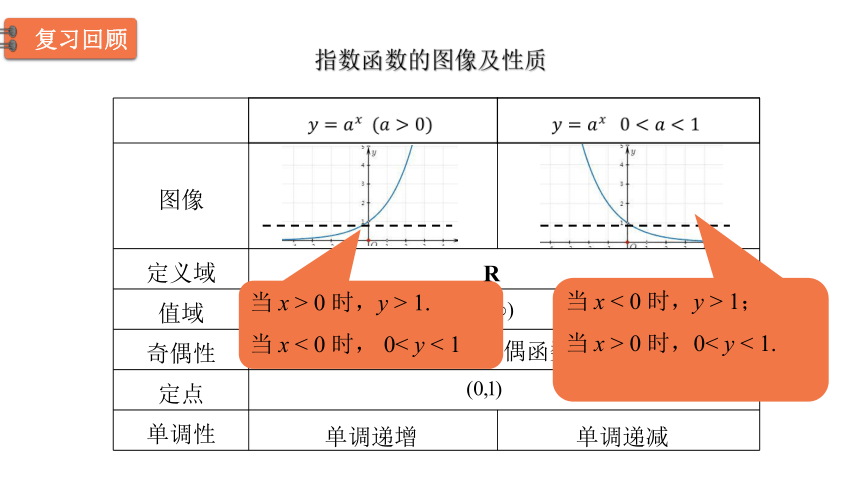
指数函数的图像及性质
非奇非偶函数
单调递增
单调递减
当 x > 0 时,y > 1.
当 x < 0 时, 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时,0< y < 1.
R
新课
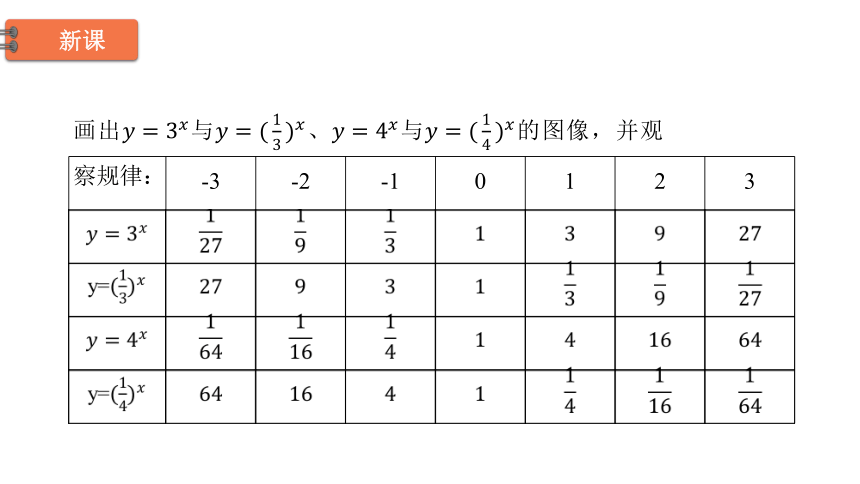
画出与、与的图像,并观察规律:
-3 -2 -1 0 1 2 3
新课
新课
问题一:底数互为倒数的两个指数函数的图像有什么联系?
问题二:底数越来越大时,指数函数的图像有什么变化?
关于y轴对称
当时:底数越大,函数值增加越快,图像越陡,越靠近轴;
当时: 底数越大,函数值增加越慢,图像越缓,越远离轴.
练一练
①
②
③
④
下图分别为,,,四个函数的图像,试将函数与图像对应:
典例精析
例1 某种放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量是原来的84%.写出这种物质的剩留量关于时间的函数关系式.
【解】设该物质最初的质量是1,经过x年剩留量是y,
经过1年,剩留量y=1×0.84=0.841;
经过2年,剩留量y=0.84×0.84=0.842;
…….
一般地,经过x年,剩留量y=0.84x(x>0,x∈N*)
典例精析
例2 某种储蓄按复利计算利息,若本金为 a 元,每期利率为 r,设存期是x
(x∈N*),本利和(本金加上利息)为 y 元.
(1)写出本利和 y 随存期 x 变化的函数关系式;
(2)已知存人本金1000元,每期利率为2.25%,试计算 5 期后的本利和.
【解】(1)已知本金为a元,利率为r,则1期后的本利和y=a+ar=a(1+r),
2期后的本利和为y=a(1+r)+a(1+r)r=a(1+r)2,
3期后的本利和为y =a(1+r)3,
………
x期后的本利和为y=a(1+r)x,x∈N*,
即本利和y随存期x变化的函数关系式为y=a(1+r)x,x∈N*.
典例精析
(2)将a=1000元,r=2.25%,x=5代入上式,得y=1000×(1+2.25%)5
=1000×1.02255≈1117.68元,即5期后的本利和约为1117.68元.
典例精析
例3 2000~2002年,我国国内生产总值年平均增长7.8%.按照这个增长速度,画出从2000年开始我国年国内生产总值随时间变化的图象,并通过图象观察到2016年我国年国内生产总值约为2000 年的多少倍(结果取整数).
【解】设2000年我国年国内生产总值是1,x年后我国年国内生产总值为y.
因为国内生产总值年平均增长7.8%,所以从2001年开始,每年的国内生产总值是上一年的1.078倍,则经过1年,y=1×1.078=1.078;
经过2年, y=1.078×1.078=1.0782;
经过3年, y=1.078×1.078=1.0782;
………..
一般地,经过x年,我国年国内生产总值y=1.078x,x∈N*.
典例精析
画出指数函数y=1.078x的图象,从图像上看出,当x=16时,y≈3.
答:到2016年我国年国内生产总值约为2000年的3倍.
1. 已知 ,则的取值范围是___________.
【解】 ∵以为底的指数函数单调递增
∵解得:
跟踪练习
2. 曲线 分别是指数函数 ,
和的图象,则与的大小关系是 ( ).
D
【解析】时,底大图高
时,底大图低
跟踪练习
跟踪练习
3. 求下列函数的定义域和值域:
(1) (2) (3)
【解】(1)定义域: 值域:
(2)定义域: 值域:
(3)定义域: 值域:
17
跟踪练习
4. 某市现有人口总数为100万人,如果年平均增长率为1.2%,试解答下列问题∶
(1)试写出 x 年后该城市人口总数 y(万人)与年份 x(年)之间的函数关系式;
(2)计算10年后该城市人口总数(精确到1万人).
【解】y=100+100×1.2%=100(1+1.2%).
2年后城市人口总数为:
y=100×(1+1.2%)+100×(1+1.2%)×1.2%=100(1+1.2%)2,
同理3年后城市人口总数为y=100(1+1.2%)3,
…
故x年后的城市人口总数为y=100(1+1.2%)x.
本节内容结束
§6.2 第2课时 指数函数的图象与性质
第六章
【教学目标】
1.通过学生自主探究,让学生总结指数函数的图像与性质.
2.能掌握指数函数的图象和性质,会用指数函数的图象和性质解决相关的问题.
3.能应用指数函数及其性质解决实际应用题.
通过学习本节内容,培养学生的逻辑推理核心素养,提升学生的数学运算核心素养.
【核心素养】
复习回顾
注意
(1)底数:大于0且不等于1的常数
(2)指数:自变量x
(3)系数:1
指数函数的定义:
一般地,函数叫做指数函数,其中 是自变量, 函数的定义域是 .
图像
定义域
值域
奇偶性
定点
单调性
复习回顾
指数函数的图像及性质
非奇非偶函数
单调递增
单调递减
当 x > 0 时,y > 1.
当 x < 0 时, 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时,0< y < 1.
R
新课
画出与、与的图像,并观察规律:
-3 -2 -1 0 1 2 3
新课
新课
问题一:底数互为倒数的两个指数函数的图像有什么联系?
问题二:底数越来越大时,指数函数的图像有什么变化?
关于y轴对称
当时:底数越大,函数值增加越快,图像越陡,越靠近轴;
当时: 底数越大,函数值增加越慢,图像越缓,越远离轴.
练一练
①
②
③
④
下图分别为,,,四个函数的图像,试将函数与图像对应:
典例精析
例1 某种放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量是原来的84%.写出这种物质的剩留量关于时间的函数关系式.
【解】设该物质最初的质量是1,经过x年剩留量是y,
经过1年,剩留量y=1×0.84=0.841;
经过2年,剩留量y=0.84×0.84=0.842;
…….
一般地,经过x年,剩留量y=0.84x(x>0,x∈N*)
典例精析
例2 某种储蓄按复利计算利息,若本金为 a 元,每期利率为 r,设存期是x
(x∈N*),本利和(本金加上利息)为 y 元.
(1)写出本利和 y 随存期 x 变化的函数关系式;
(2)已知存人本金1000元,每期利率为2.25%,试计算 5 期后的本利和.
【解】(1)已知本金为a元,利率为r,则1期后的本利和y=a+ar=a(1+r),
2期后的本利和为y=a(1+r)+a(1+r)r=a(1+r)2,
3期后的本利和为y =a(1+r)3,
………
x期后的本利和为y=a(1+r)x,x∈N*,
即本利和y随存期x变化的函数关系式为y=a(1+r)x,x∈N*.
典例精析
(2)将a=1000元,r=2.25%,x=5代入上式,得y=1000×(1+2.25%)5
=1000×1.02255≈1117.68元,即5期后的本利和约为1117.68元.
典例精析
例3 2000~2002年,我国国内生产总值年平均增长7.8%.按照这个增长速度,画出从2000年开始我国年国内生产总值随时间变化的图象,并通过图象观察到2016年我国年国内生产总值约为2000 年的多少倍(结果取整数).
【解】设2000年我国年国内生产总值是1,x年后我国年国内生产总值为y.
因为国内生产总值年平均增长7.8%,所以从2001年开始,每年的国内生产总值是上一年的1.078倍,则经过1年,y=1×1.078=1.078;
经过2年, y=1.078×1.078=1.0782;
经过3年, y=1.078×1.078=1.0782;
………..
一般地,经过x年,我国年国内生产总值y=1.078x,x∈N*.
典例精析
画出指数函数y=1.078x的图象,从图像上看出,当x=16时,y≈3.
答:到2016年我国年国内生产总值约为2000年的3倍.
1. 已知 ,则的取值范围是___________.
【解】 ∵以为底的指数函数单调递增
∵解得:
跟踪练习
2. 曲线 分别是指数函数 ,
和的图象,则与的大小关系是 ( ).
D
【解析】时,底大图高
时,底大图低
跟踪练习
跟踪练习
3. 求下列函数的定义域和值域:
(1) (2) (3)
【解】(1)定义域: 值域:
(2)定义域: 值域:
(3)定义域: 值域:
17
跟踪练习
4. 某市现有人口总数为100万人,如果年平均增长率为1.2%,试解答下列问题∶
(1)试写出 x 年后该城市人口总数 y(万人)与年份 x(年)之间的函数关系式;
(2)计算10年后该城市人口总数(精确到1万人).
【解】y=100+100×1.2%=100(1+1.2%).
2年后城市人口总数为:
y=100×(1+1.2%)+100×(1+1.2%)×1.2%=100(1+1.2%)2,
同理3年后城市人口总数为y=100(1+1.2%)3,
…
故x年后的城市人口总数为y=100(1+1.2%)x.
本节内容结束
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
