第一章 功和机械能大单元备课 课件(共28张PPT)鲁科版(2019)必修第二册
文档属性
| 名称 | 第一章 功和机械能大单元备课 课件(共28张PPT)鲁科版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-16 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
第一章 功和机械能
【知识要点】
一、功
二、功率
三、动能和动能定理
四、势能及其改变
五、机械能守恒定律
六、功能关系
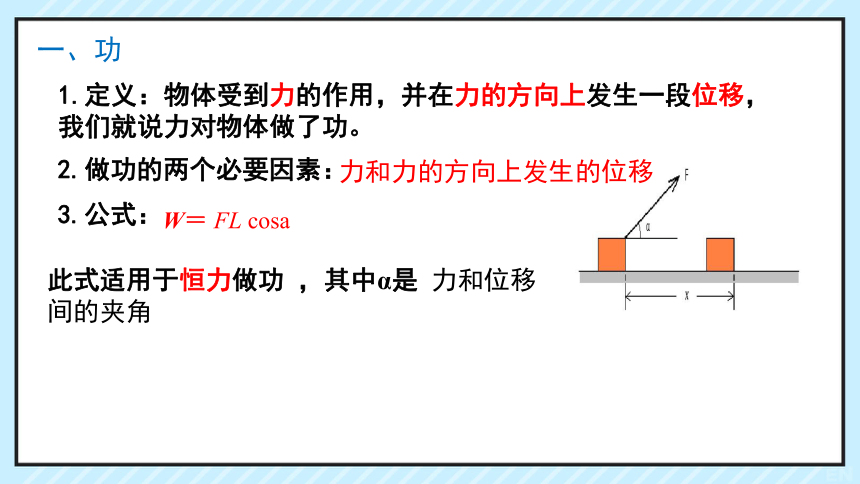
一、功
1.定义:物体受到力的作用,并在力的方向上发生一段位移,
我们就说力对物体做了功。
2.做功的两个必要因素:
力和力的方向上发生的位移
3.公式:
W= FL cosa
此式适用于恒力做功 ,其中α是 力和位移间的夹角
4.功的正负
(1)正负号的意义:
功是标量 ,但有正负之分,功的正负表示动力对物体做功还是阻力对物体做功。比较功的大小时,只比较其绝对值的大小。
(2)力对物体做正、负功的判断
①0≤α<90°时: W>0,力对物体做正功 。
②90°<α≤180°时: W<0,力对物体做负功 ,也可以说物体克服外力做了功。
③α=90°时: W=0,力对物体不做功
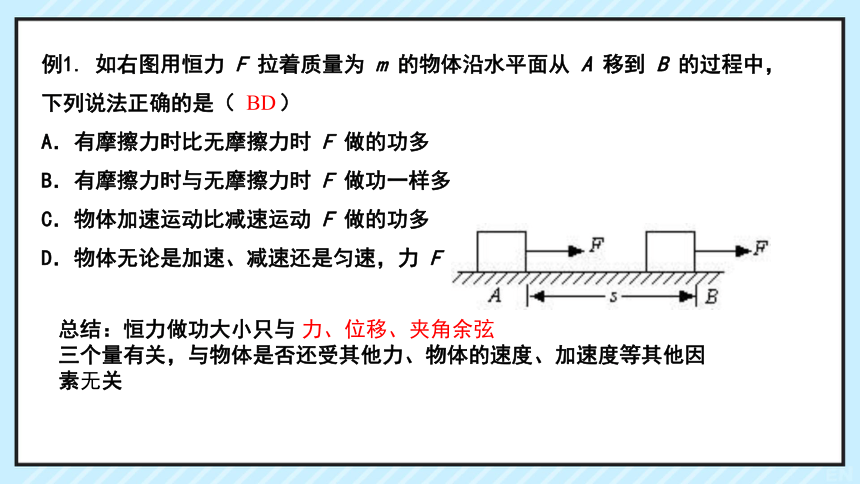
例1. 如右图用恒力 F 拉着质量为 m 的物体沿水平面从 A 移到 B 的过程中,下列说法正确的是( )
A.有摩擦力时比无摩擦力时 F 做的功多
B.有摩擦力时与无摩擦力时 F 做功一样多
C.物体加速运动比减速运动 F 做的功多
D.物体无论是加速、减速还是匀速,力 F 做的功一样多
总结:恒力做功大小只与 三个量有关,与物体是否还受其他力、物体的速度、加速度等其他因素无关
力、位移、夹角余弦
BD
例2.如右图所示,小物块 A 位于光滑的斜面上,斜面位于光滑的水平面上,从地面上看,小物块沿斜面下滑的过程中,斜面对小物块的作用力( )
A.垂直于接触面,做功为零
B.垂直于接触面,做功不为零
C.不垂直于接触面,做功为零
D.不垂直于接触面,做功不为零
B
总结:判断力的做功情况的方法有:
1.看力与物体的位移(或速度)之间的夹角α的大小;
2.看物体间的能量变化情况,若有能量转化,则必有力做功,此法常用于两个相联系的物体的情况。
例3. 如图,质量为m的小物体静止于长为L的木板边缘,现使板由水平放置绕其另一端O沿逆时针方向缓缓转过α角,转动过程中,小物体相对板始终静止,对于这个过程中各力做功的情况,下列说法中正确的是( )
A.摩擦力对物体所做的功为 mgLsinα(1-cosα)
B.弹力对物体所做的功为 mgLsinα
C.重力对物体所做的功为 mgLsinα
D.合力对物体所做的功为 mgLcosα
G
f
N
总结:变力做功的求法:
图像法 平均值法 动能定理
B
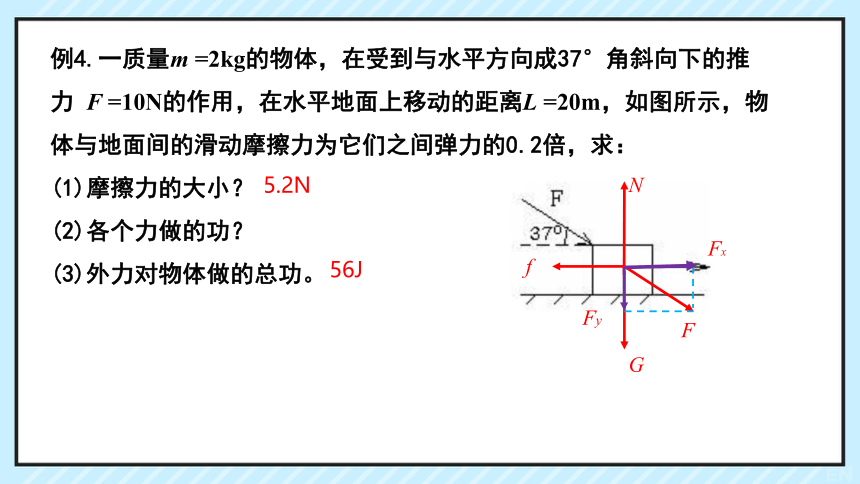
例4.一质量m =2kg的物体,在受到与水平方向成37°角斜向下的推力 F =10N的作用,在水平地面上移动的距离L =20m,如图所示,物体与地面间的滑动摩擦力为它们之间弹力的0.2倍,求:
(1)摩擦力的大小?
(2)各个力做的功?
(3)外力对物体做的总功。
56J
5.2N
G
N
f
F
Fx
Fy
总结:如果物体同时受多个恒力作用,计算合外力功的方法有哪些?
一是先求出 ,再根据 计算功,注意此时的 α 应为 与 间的夹角;
二是先分别求出各个力的 ,再把各个力的功
合力
W 合 =F 合 L cosα
合力
位移
功
求代数和
二、功率
1.定义:功率是表示物体 的物理量,是力所做的功与完成这些功所用时间的比值。
做功快慢
2.公式:
结合W=Flcosα得:推导公式功率的P= ,
Fv cosα
其中α是F与v方向之间的夹角,v是物体相对地
(1)若v是物体的瞬时速度,则P=Fvcosα计算瞬时功率;
(2)若v是物体的平均速度,则P=Fvcosα计算平均功率。
3.额定功率与实际功率
(1)额定功率:机械长时间正常工作而不损坏机械的最大输出功率。
(2)实际功率:机器实际工作时的输出功率。
注意:a、一般机器铭牌上标明的功率表示该机器的额定功率。
b、实际功率一般小于或等于额定功率。
例5.(多选)质量为 m 的物体从距地面高 h 处自由下落,经历时间 t ,则下列说法正确的是( )
A.t秒内重力对物体做功为
B.t秒钟内重力的平均功率为
C.前秒末重力的瞬时功率与后秒末重力的瞬时功率之比为 1∶2
D.前 秒内重力做功的平均功率与后秒内重力做功的平均 功率之比为1∶3
ACD
例6. (多选)如图所示,三个相同的小球A、B、C ,其中小球A沿高为h、倾角为θ的光滑斜面以初速度v0从顶端滑到底端,小球B以同样大小的初速度从同等高度处竖直上抛,小球 C 在同等高度水平抛出。则( )
A.小球 A 到达地面的速度最大
B.从开始至落地,重力对它们做功相同
C.三个小球到达地面时,小球 B 重力的瞬时功率最大
D.从开始运动至落地过程中,重力对它们做功的平均功率一定相同
BC
4、机车的两种启动
例7.某汽车发动机的额定功率为60kW,汽车质量为5t,汽车在运动中所受阻力的大小恒为车重的0.1倍。(g 取)
(1)若汽车以额定功率启动,则汽车所能达到的最大速度是多少?当汽车速度达到5m/s时,其加速度是多少?(画出全过程的 v - t 图)
(2)若汽车以恒定加速度0.5 启动,则其匀加速过程能维持多长时间?(画出全过程的 v-t 图)
总结⑥:机车的启动问题:
(1)无论哪种启动,机车的最大速度都等于其 时的速度,即 =
(2)机车的加速度 a 由 决定,即表达式
匀速
P 额 /f
合外力
三、机械能
1.动能:
2.重力势能:
(与参考平面选取有关)
重力做功只与初末位置的高度有关,与路径无关。
单位: ;矢标量: 量,也有正负之分
重力做功与重力势能变化量之间的关系:
J
矢
3.弹性势能
(1)概念:物体由于发生 而具有的能。大小与 有关
(2)弹力做功与弹性势能变化的关系:
弹性形变
形变量
劲度系数、
例8. 质量为m的小球,从离桌面H高处由静止下落,桌面离地的高度为h,如图所示,若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别( )
A.mgh,减少mg( H - h )
B.mgh ,增加mg( H + h )
C.-mgh ,增加mg( H - h )
D.-mgh ,减少mg( H + h )
总结:重力势能的大小和参考平面的选取有关,而重力势能的变化与参考平面的选取无关
D
总结:重力做功与重力势能的关系:
重力做正功,重力势能 ;
重力做负功,重力势能 。
减少
增加
例9. (多选)如图所示,一个物体以速度v 0 冲向与竖直墙壁相连的轻质弹簧,弹簧被物体压缩, 在此过程中 以下说法正确的是( )
A.物体对弹簧所做的功与弹簧的压缩量成正比
B.物体向墙壁运动相同的位移,弹力做的功不相等
C.弹簧的弹力做正功,弹簧的弹性势能减小
D.弹簧的弹力做负功,弹簧的弹性势能增加
总结:弹力做正功,弹性势能 减少;
弹力做负功,弹性势能增加。
BD
四、功能关系
1.动能定理:
力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
2.表达式:
(如果物体受到几个力的共同作用,动能定理中的W即为合力做的功)
3.应用动能定理解题的步骤:
(1)确定研究对象和研究过程。动能定理的研究对象只能是单个物体,如果是系统,那么系统内的物体间不能有相对运动。
(2)对研究对象进行受力分析。(研究对象以外的物体施于研究对象的力都要分析,含重力)。
(3)写出该过程中合外力做的功,或分别写出各个力做的功(注意功的正负)。如果研究过程中物体受力情况有变化,要分别写出该力在各个阶段做的功。
(4)写出物体的初、末动能。
(5)按照动能定理列式求解。
例10. 如图所示,斜面倾角为α,长为L,AB段光滑,BC段粗糙,且BC=2AB。质量为m的木块从斜面顶端无初速度下滑,到达C端时速度刚好减小到零。求物体和斜面BC段间的动摩擦因数μ。
找出各力做的功,用动能定理求解
例11、在平直公路上,汽车由静止开始作匀加速运动,当速度达到某一值时,立即关闭发动机后滑行至停止,其v-t图像如图所示.汽车牵引力为F,运动过程中所受的摩擦阻力恒为f,全过程中牵引力所做的功为W1,克服摩擦阻力所做的功为W2,则下列关系中正确的是( ).
(A)F:f=1:3
(B)F:f=4:1
(C)W1:W2=1:1
(D)W1:W2=1:3
B
五、机械能守恒定律
在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械能保持不变.这就是机械能守恒定律.
1.条件:只有重力或系统内弹力做功
2.表达式:
ΔEA增=ΔEB减,适用于系统,表示由A、B组成的系统,A部分机械能的增加量与B部分机械能的减少量相等.
3.用机械能守恒定律解题的一般步骤
(1).选取研究对象——系统或物体.
(2).根据研究对象所经历的物理过程.进行受力、做功分析,判断机械能是否守恒.
(3).恰当地选取参考平面,确定研究对象在过程的初末状态时的机械能.
(4).根据机械能守恒定律列方程,进行求解.
例11. 如图所示,物体A质量为2m,物体B质量为m,通过轻绳跨过定滑轮相连.斜面光滑,且与水平面成θ=30°,不计绳子和滑轮之间的摩擦.开始时A物体离地的高度为h,B物体位于斜面的底端,用手托住A物体,A、B两物体均静止.撤去手后,求:
(1)A物体将要落地时的速度多大?
(2)A物落地后,B物由于惯性将继续沿斜面上升,
则B物在斜面上的最远点离地的高度多大?
系统机械能守恒
h
例12. 如图所示,质量m为2kg的物体,从光滑斜面的顶端A点以=5m/s的初速度滑下,在D点与弹簧接触并将弹簧压缩到B点时的速度为零,已知从A到B的竖直高度h=5m,求弹簧的弹力对物体所做的功。
设弹力做功为 W F ,找出各力做的功,再用动能定理求解
-125J
第一章 功和机械能
【知识要点】
一、功
二、功率
三、动能和动能定理
四、势能及其改变
五、机械能守恒定律
六、功能关系
一、功
1.定义:物体受到力的作用,并在力的方向上发生一段位移,
我们就说力对物体做了功。
2.做功的两个必要因素:
力和力的方向上发生的位移
3.公式:
W= FL cosa
此式适用于恒力做功 ,其中α是 力和位移间的夹角
4.功的正负
(1)正负号的意义:
功是标量 ,但有正负之分,功的正负表示动力对物体做功还是阻力对物体做功。比较功的大小时,只比较其绝对值的大小。
(2)力对物体做正、负功的判断
①0≤α<90°时: W>0,力对物体做正功 。
②90°<α≤180°时: W<0,力对物体做负功 ,也可以说物体克服外力做了功。
③α=90°时: W=0,力对物体不做功
例1. 如右图用恒力 F 拉着质量为 m 的物体沿水平面从 A 移到 B 的过程中,下列说法正确的是( )
A.有摩擦力时比无摩擦力时 F 做的功多
B.有摩擦力时与无摩擦力时 F 做功一样多
C.物体加速运动比减速运动 F 做的功多
D.物体无论是加速、减速还是匀速,力 F 做的功一样多
总结:恒力做功大小只与 三个量有关,与物体是否还受其他力、物体的速度、加速度等其他因素无关
力、位移、夹角余弦
BD
例2.如右图所示,小物块 A 位于光滑的斜面上,斜面位于光滑的水平面上,从地面上看,小物块沿斜面下滑的过程中,斜面对小物块的作用力( )
A.垂直于接触面,做功为零
B.垂直于接触面,做功不为零
C.不垂直于接触面,做功为零
D.不垂直于接触面,做功不为零
B
总结:判断力的做功情况的方法有:
1.看力与物体的位移(或速度)之间的夹角α的大小;
2.看物体间的能量变化情况,若有能量转化,则必有力做功,此法常用于两个相联系的物体的情况。
例3. 如图,质量为m的小物体静止于长为L的木板边缘,现使板由水平放置绕其另一端O沿逆时针方向缓缓转过α角,转动过程中,小物体相对板始终静止,对于这个过程中各力做功的情况,下列说法中正确的是( )
A.摩擦力对物体所做的功为 mgLsinα(1-cosα)
B.弹力对物体所做的功为 mgLsinα
C.重力对物体所做的功为 mgLsinα
D.合力对物体所做的功为 mgLcosα
G
f
N
总结:变力做功的求法:
图像法 平均值法 动能定理
B
例4.一质量m =2kg的物体,在受到与水平方向成37°角斜向下的推力 F =10N的作用,在水平地面上移动的距离L =20m,如图所示,物体与地面间的滑动摩擦力为它们之间弹力的0.2倍,求:
(1)摩擦力的大小?
(2)各个力做的功?
(3)外力对物体做的总功。
56J
5.2N
G
N
f
F
Fx
Fy
总结:如果物体同时受多个恒力作用,计算合外力功的方法有哪些?
一是先求出 ,再根据 计算功,注意此时的 α 应为 与 间的夹角;
二是先分别求出各个力的 ,再把各个力的功
合力
W 合 =F 合 L cosα
合力
位移
功
求代数和
二、功率
1.定义:功率是表示物体 的物理量,是力所做的功与完成这些功所用时间的比值。
做功快慢
2.公式:
结合W=Flcosα得:推导公式功率的P= ,
Fv cosα
其中α是F与v方向之间的夹角,v是物体相对地
(1)若v是物体的瞬时速度,则P=Fvcosα计算瞬时功率;
(2)若v是物体的平均速度,则P=Fvcosα计算平均功率。
3.额定功率与实际功率
(1)额定功率:机械长时间正常工作而不损坏机械的最大输出功率。
(2)实际功率:机器实际工作时的输出功率。
注意:a、一般机器铭牌上标明的功率表示该机器的额定功率。
b、实际功率一般小于或等于额定功率。
例5.(多选)质量为 m 的物体从距地面高 h 处自由下落,经历时间 t ,则下列说法正确的是( )
A.t秒内重力对物体做功为
B.t秒钟内重力的平均功率为
C.前秒末重力的瞬时功率与后秒末重力的瞬时功率之比为 1∶2
D.前 秒内重力做功的平均功率与后秒内重力做功的平均 功率之比为1∶3
ACD
例6. (多选)如图所示,三个相同的小球A、B、C ,其中小球A沿高为h、倾角为θ的光滑斜面以初速度v0从顶端滑到底端,小球B以同样大小的初速度从同等高度处竖直上抛,小球 C 在同等高度水平抛出。则( )
A.小球 A 到达地面的速度最大
B.从开始至落地,重力对它们做功相同
C.三个小球到达地面时,小球 B 重力的瞬时功率最大
D.从开始运动至落地过程中,重力对它们做功的平均功率一定相同
BC
4、机车的两种启动
例7.某汽车发动机的额定功率为60kW,汽车质量为5t,汽车在运动中所受阻力的大小恒为车重的0.1倍。(g 取)
(1)若汽车以额定功率启动,则汽车所能达到的最大速度是多少?当汽车速度达到5m/s时,其加速度是多少?(画出全过程的 v - t 图)
(2)若汽车以恒定加速度0.5 启动,则其匀加速过程能维持多长时间?(画出全过程的 v-t 图)
总结⑥:机车的启动问题:
(1)无论哪种启动,机车的最大速度都等于其 时的速度,即 =
(2)机车的加速度 a 由 决定,即表达式
匀速
P 额 /f
合外力
三、机械能
1.动能:
2.重力势能:
(与参考平面选取有关)
重力做功只与初末位置的高度有关,与路径无关。
单位: ;矢标量: 量,也有正负之分
重力做功与重力势能变化量之间的关系:
J
矢
3.弹性势能
(1)概念:物体由于发生 而具有的能。大小与 有关
(2)弹力做功与弹性势能变化的关系:
弹性形变
形变量
劲度系数、
例8. 质量为m的小球,从离桌面H高处由静止下落,桌面离地的高度为h,如图所示,若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别( )
A.mgh,减少mg( H - h )
B.mgh ,增加mg( H + h )
C.-mgh ,增加mg( H - h )
D.-mgh ,减少mg( H + h )
总结:重力势能的大小和参考平面的选取有关,而重力势能的变化与参考平面的选取无关
D
总结:重力做功与重力势能的关系:
重力做正功,重力势能 ;
重力做负功,重力势能 。
减少
增加
例9. (多选)如图所示,一个物体以速度v 0 冲向与竖直墙壁相连的轻质弹簧,弹簧被物体压缩, 在此过程中 以下说法正确的是( )
A.物体对弹簧所做的功与弹簧的压缩量成正比
B.物体向墙壁运动相同的位移,弹力做的功不相等
C.弹簧的弹力做正功,弹簧的弹性势能减小
D.弹簧的弹力做负功,弹簧的弹性势能增加
总结:弹力做正功,弹性势能 减少;
弹力做负功,弹性势能增加。
BD
四、功能关系
1.动能定理:
力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
2.表达式:
(如果物体受到几个力的共同作用,动能定理中的W即为合力做的功)
3.应用动能定理解题的步骤:
(1)确定研究对象和研究过程。动能定理的研究对象只能是单个物体,如果是系统,那么系统内的物体间不能有相对运动。
(2)对研究对象进行受力分析。(研究对象以外的物体施于研究对象的力都要分析,含重力)。
(3)写出该过程中合外力做的功,或分别写出各个力做的功(注意功的正负)。如果研究过程中物体受力情况有变化,要分别写出该力在各个阶段做的功。
(4)写出物体的初、末动能。
(5)按照动能定理列式求解。
例10. 如图所示,斜面倾角为α,长为L,AB段光滑,BC段粗糙,且BC=2AB。质量为m的木块从斜面顶端无初速度下滑,到达C端时速度刚好减小到零。求物体和斜面BC段间的动摩擦因数μ。
找出各力做的功,用动能定理求解
例11、在平直公路上,汽车由静止开始作匀加速运动,当速度达到某一值时,立即关闭发动机后滑行至停止,其v-t图像如图所示.汽车牵引力为F,运动过程中所受的摩擦阻力恒为f,全过程中牵引力所做的功为W1,克服摩擦阻力所做的功为W2,则下列关系中正确的是( ).
(A)F:f=1:3
(B)F:f=4:1
(C)W1:W2=1:1
(D)W1:W2=1:3
B
五、机械能守恒定律
在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械能保持不变.这就是机械能守恒定律.
1.条件:只有重力或系统内弹力做功
2.表达式:
ΔEA增=ΔEB减,适用于系统,表示由A、B组成的系统,A部分机械能的增加量与B部分机械能的减少量相等.
3.用机械能守恒定律解题的一般步骤
(1).选取研究对象——系统或物体.
(2).根据研究对象所经历的物理过程.进行受力、做功分析,判断机械能是否守恒.
(3).恰当地选取参考平面,确定研究对象在过程的初末状态时的机械能.
(4).根据机械能守恒定律列方程,进行求解.
例11. 如图所示,物体A质量为2m,物体B质量为m,通过轻绳跨过定滑轮相连.斜面光滑,且与水平面成θ=30°,不计绳子和滑轮之间的摩擦.开始时A物体离地的高度为h,B物体位于斜面的底端,用手托住A物体,A、B两物体均静止.撤去手后,求:
(1)A物体将要落地时的速度多大?
(2)A物落地后,B物由于惯性将继续沿斜面上升,
则B物在斜面上的最远点离地的高度多大?
系统机械能守恒
h
例12. 如图所示,质量m为2kg的物体,从光滑斜面的顶端A点以=5m/s的初速度滑下,在D点与弹簧接触并将弹簧压缩到B点时的速度为零,已知从A到B的竖直高度h=5m,求弹簧的弹力对物体所做的功。
设弹力做功为 W F ,找出各力做的功,再用动能定理求解
-125J
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
