5.7 扇形(课件)人教版六年级上册数学(共25张PPT)
文档属性
| 名称 | 5.7 扇形(课件)人教版六年级上册数学(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 16:36:49 | ||
图片预览

文档简介
(共25张PPT)
扇 形
5
R·六年级上册
新课导入
各种各样美丽的扇形图案:
什么是扇形?
这些物体的名称有什么共同点?
名称里都有“扇”字。
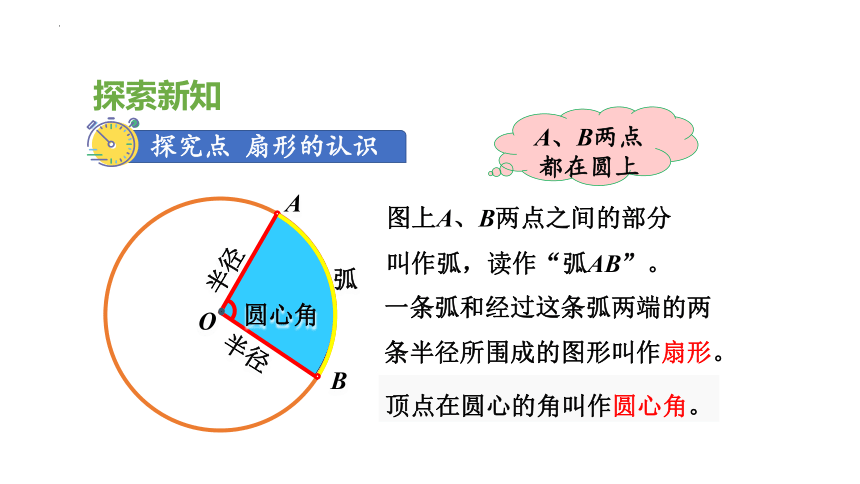
探索新知
探究点 扇形的认识
A
B
O
圆心角
半径
半径
弧
图上A、B两点之间的部分
叫作弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。
顶点在圆心的角叫作圆心角。
A、B两点都在圆上
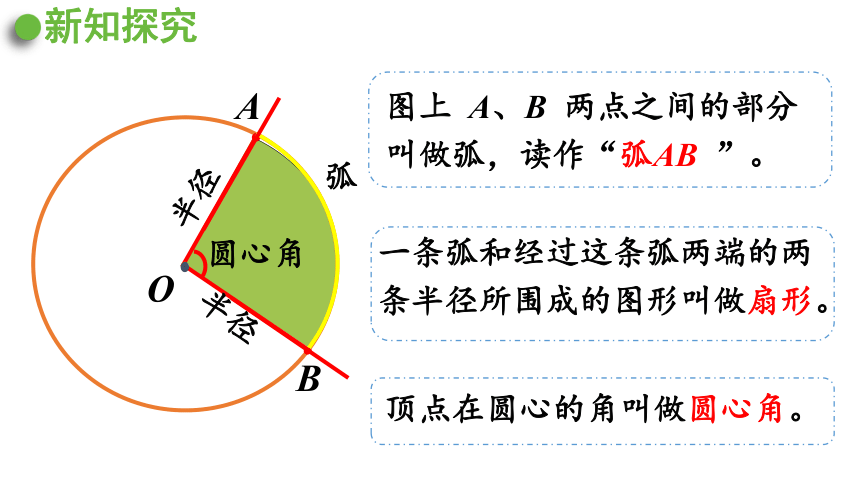
新知探究
A
B
O
圆心角
半径
半径
弧
图上 A、B 两点之间的部分叫做弧,读作“弧AB ”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
以半圆为弧的扇形的圆心角是180°。
O
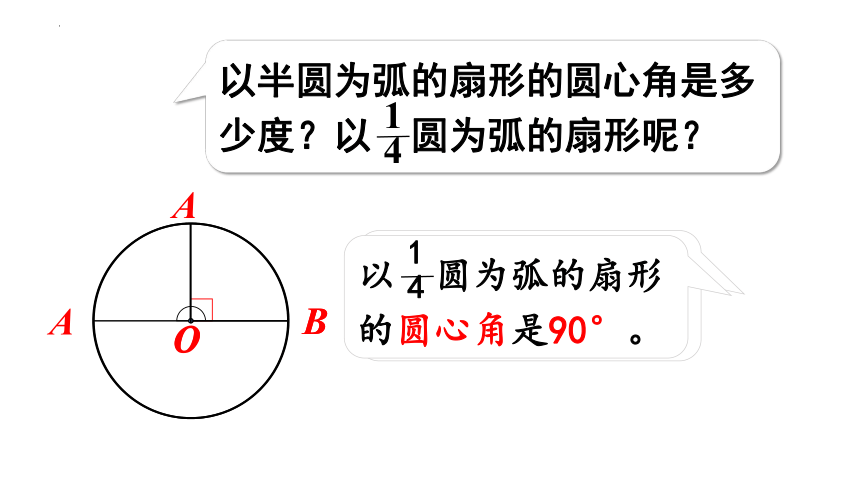
以半圆为弧的扇形的圆心角是多少度?以 圆为弧的扇形呢?
1
4
A
B
O
A
B
以 圆为弧的扇形的圆心角是90°。
1
4
探索新知
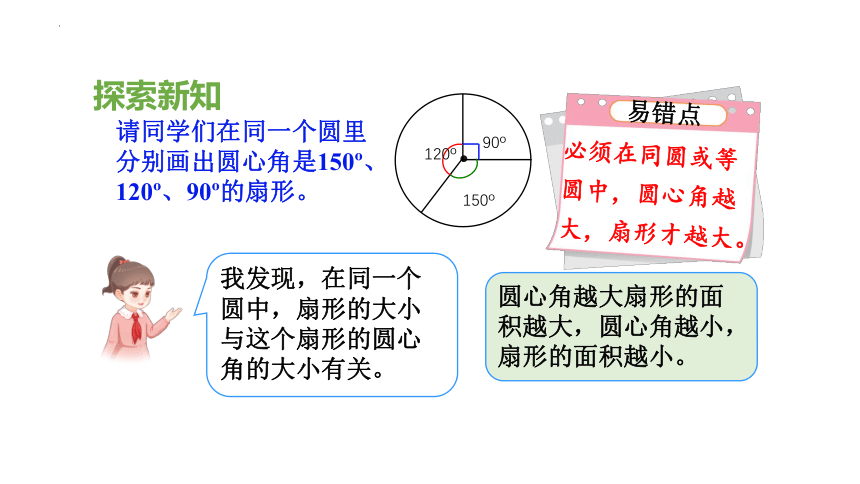
我发现,在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
请同学们在同一个圆里
分别画出圆心角是150 、
120 、90 的扇形。
必须在同圆或等圆中,圆心角越大,扇形才越大。
易错点
120
150
90
圆心角越大扇形的面积越大,圆心角越小,扇形的面积越小。
O
A
O
B
A
B
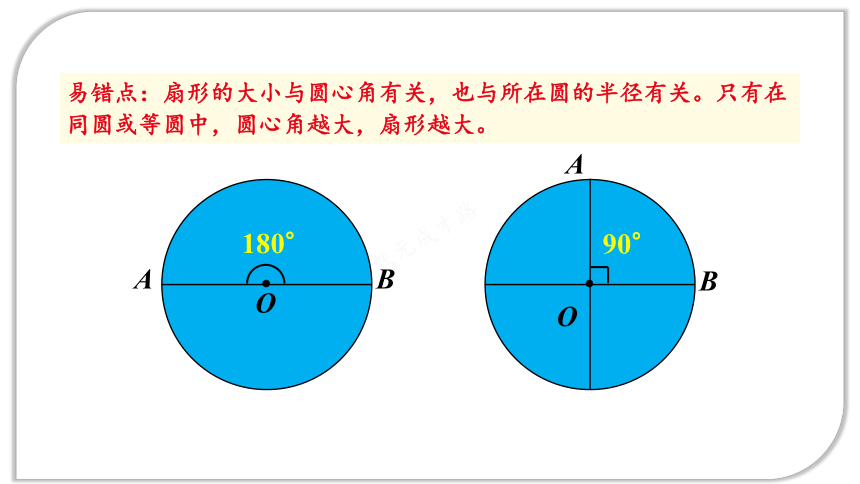
180°
90°
易错点:扇形的大小与圆心角有关,也与所在圆的半径有关。只有在同圆或等圆中,圆心角越大,扇形越大。
探索新知
180°
90°
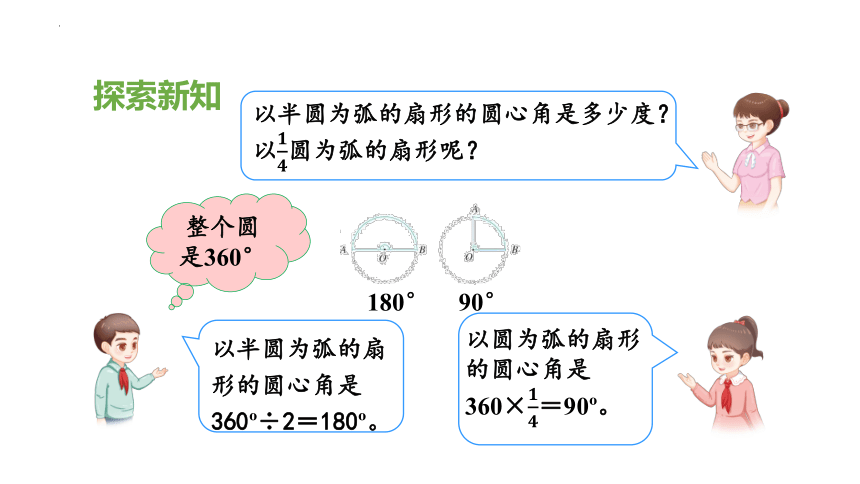
整个圆是360°
以半圆为弧的扇形的圆心角是多少度?
以圆为弧的扇形呢?
以半圆为弧的扇形的圆心角是360 ÷2=180 。
以圆为弧的扇形的圆心角是360×=90 。
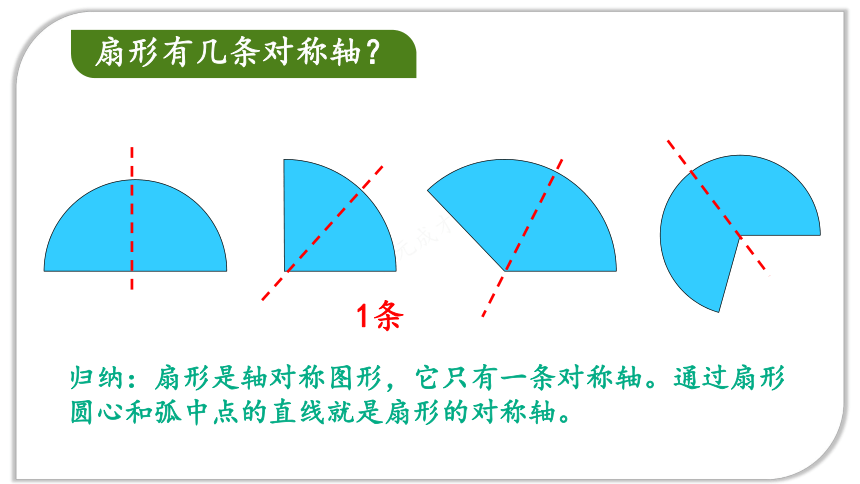
1条
扇形有几条对称轴?
归纳:扇形是轴对称图形,它只有一条对称轴。通过扇形圆心和弧中点的直线就是扇形的对称轴。
你会求扇形的面积吗?
归纳:
扇形的周长=弧长+半径×2
1.下面图形的阴影部分是扇形的在( )里画“√”。
探索新知
小试牛刀
2.下面图形中哪些角是圆心角?在( )里画“√”。
探索新知
小试牛刀
1.下列图形中的扇形是几分之几圆?
( )
( )
( )
1
2
1
4
1
5
课堂练习
2.判对错。
(1)一个圆上有无数条弧。( )
(2)扇形是圆的一部分,圆的一部分一定是
扇形。( )
(3)顶点在圆心上的角叫做圆心角。( )
(4)圆心角越大,扇形的面积越大。( )
(5)扇形有无数条对称轴。( )
√
×
√
×
×
3. 先画一个半径是2 cm的圆,再在圆中画一个圆
心角是100°的扇形。
教材第74页“练习十六”第3题
2厘米
100°
1.画一个半径2 cm
的圆。
2.画一条半径,并
以半径为边,画
一个100°的角。
3.14×2
4.下面三个圆的半径都是2厘米,每个圆中阴影
部分的面积是多少?(只列式,不计算)
3.14×2 ÷2
3.14×2 ÷4
把整个圆的面积看作一个整体。
阴影部分的面积占整个圆面积的( )。
1
2
阴影部分的面积占整个圆面积的( )。
1
4
像下面这样一个圆环被截得的部分叫做扇环。你能求出下面各扇环的面积吗?
S扇环=
S扇环=
拓展延伸,认识扇环
当堂练习
1.汽车上有雨刷装置,如果一个雨刷呈扇形摆动刮出的区域是如图所示的阴影部分,那么这个雨刷刮出的区域的面积是多少?
3.14×[402-(40-30)2]×=1177.5(cm2)
答:这个雨刷刮出的区域的面积是1177.5 cm2。
当堂练习
2.(易错题)已知直角梯形的上底是10厘米,下底是14厘米,每个扇形的半径为4厘米。求四个扇形的面积和。
梯形中的四个扇形刚好拼成一个圆。
3.14×42=50.24(平方厘米)
答:四个扇形的面积和是50.24平方厘米。
一、观察下列图形,哪些涂色部分是扇形?在括号里画“√”。
√
√
课堂小结
二、判一判。(对的画“√”,错的画“×")
1.扇形是圆的一部分,圆的一部分不一定是扇形。
( )
2.扇形是轴对称图形,它有一条对称轴。 ( )
3.用6个圆心角都是60°的扇形,一定可以拼成一个圆。
( )
4.圆心角越大,扇形的面积就越大。 ( )
5.在一个圆中剪去一个扇形后,剩下的部分一定是扇形。
( )
√
√
×
×
√
1. 指出下列物体中的扇形。
[教材P74 练习十六 第1题]
巩固运用,拓展深化
2.下面图形中哪些角是圆心角?在( )里画“√”。
√
×
×
√
[教材P74 练习十六 第2题]
易错点:圆心角必须具备两个条件:①顶点在圆心;②角的两边是圆的半径。
课堂总结
1. 判断圆心角的依据:
(1)圆心角的两条边是圆的两条半径。
(2)圆心角的顶点是圆心。
2. 决定扇形大小的因素:圆心角和扇形所在圆的半径。
3. 特殊的扇形:以半圆为弧的扇形的圆心角是180°;
以一圆为弧的扇形的圆心角是:90°
thank you!
扇 形
5
R·六年级上册
新课导入
各种各样美丽的扇形图案:
什么是扇形?
这些物体的名称有什么共同点?
名称里都有“扇”字。
探索新知
探究点 扇形的认识
A
B
O
圆心角
半径
半径
弧
图上A、B两点之间的部分
叫作弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。
顶点在圆心的角叫作圆心角。
A、B两点都在圆上
新知探究
A
B
O
圆心角
半径
半径
弧
图上 A、B 两点之间的部分叫做弧,读作“弧AB ”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
以半圆为弧的扇形的圆心角是180°。
O
以半圆为弧的扇形的圆心角是多少度?以 圆为弧的扇形呢?
1
4
A
B
O
A
B
以 圆为弧的扇形的圆心角是90°。
1
4
探索新知
我发现,在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
请同学们在同一个圆里
分别画出圆心角是150 、
120 、90 的扇形。
必须在同圆或等圆中,圆心角越大,扇形才越大。
易错点
120
150
90
圆心角越大扇形的面积越大,圆心角越小,扇形的面积越小。
O
A
O
B
A
B
180°
90°
易错点:扇形的大小与圆心角有关,也与所在圆的半径有关。只有在同圆或等圆中,圆心角越大,扇形越大。
探索新知
180°
90°
整个圆是360°
以半圆为弧的扇形的圆心角是多少度?
以圆为弧的扇形呢?
以半圆为弧的扇形的圆心角是360 ÷2=180 。
以圆为弧的扇形的圆心角是360×=90 。
1条
扇形有几条对称轴?
归纳:扇形是轴对称图形,它只有一条对称轴。通过扇形圆心和弧中点的直线就是扇形的对称轴。
你会求扇形的面积吗?
归纳:
扇形的周长=弧长+半径×2
1.下面图形的阴影部分是扇形的在( )里画“√”。
探索新知
小试牛刀
2.下面图形中哪些角是圆心角?在( )里画“√”。
探索新知
小试牛刀
1.下列图形中的扇形是几分之几圆?
( )
( )
( )
1
2
1
4
1
5
课堂练习
2.判对错。
(1)一个圆上有无数条弧。( )
(2)扇形是圆的一部分,圆的一部分一定是
扇形。( )
(3)顶点在圆心上的角叫做圆心角。( )
(4)圆心角越大,扇形的面积越大。( )
(5)扇形有无数条对称轴。( )
√
×
√
×
×
3. 先画一个半径是2 cm的圆,再在圆中画一个圆
心角是100°的扇形。
教材第74页“练习十六”第3题
2厘米
100°
1.画一个半径2 cm
的圆。
2.画一条半径,并
以半径为边,画
一个100°的角。
3.14×2
4.下面三个圆的半径都是2厘米,每个圆中阴影
部分的面积是多少?(只列式,不计算)
3.14×2 ÷2
3.14×2 ÷4
把整个圆的面积看作一个整体。
阴影部分的面积占整个圆面积的( )。
1
2
阴影部分的面积占整个圆面积的( )。
1
4
像下面这样一个圆环被截得的部分叫做扇环。你能求出下面各扇环的面积吗?
S扇环=
S扇环=
拓展延伸,认识扇环
当堂练习
1.汽车上有雨刷装置,如果一个雨刷呈扇形摆动刮出的区域是如图所示的阴影部分,那么这个雨刷刮出的区域的面积是多少?
3.14×[402-(40-30)2]×=1177.5(cm2)
答:这个雨刷刮出的区域的面积是1177.5 cm2。
当堂练习
2.(易错题)已知直角梯形的上底是10厘米,下底是14厘米,每个扇形的半径为4厘米。求四个扇形的面积和。
梯形中的四个扇形刚好拼成一个圆。
3.14×42=50.24(平方厘米)
答:四个扇形的面积和是50.24平方厘米。
一、观察下列图形,哪些涂色部分是扇形?在括号里画“√”。
√
√
课堂小结
二、判一判。(对的画“√”,错的画“×")
1.扇形是圆的一部分,圆的一部分不一定是扇形。
( )
2.扇形是轴对称图形,它有一条对称轴。 ( )
3.用6个圆心角都是60°的扇形,一定可以拼成一个圆。
( )
4.圆心角越大,扇形的面积就越大。 ( )
5.在一个圆中剪去一个扇形后,剩下的部分一定是扇形。
( )
√
√
×
×
√
1. 指出下列物体中的扇形。
[教材P74 练习十六 第1题]
巩固运用,拓展深化
2.下面图形中哪些角是圆心角?在( )里画“√”。
√
×
×
√
[教材P74 练习十六 第2题]
易错点:圆心角必须具备两个条件:①顶点在圆心;②角的两边是圆的半径。
课堂总结
1. 判断圆心角的依据:
(1)圆心角的两条边是圆的两条半径。
(2)圆心角的顶点是圆心。
2. 决定扇形大小的因素:圆心角和扇形所在圆的半径。
3. 特殊的扇形:以半圆为弧的扇形的圆心角是180°;
以一圆为弧的扇形的圆心角是:90°
thank you!
