人教版高中数学必修第二册10.3频率与概率 课件(共28张PPT)
文档属性
| 名称 | 人教版高中数学必修第二册10.3频率与概率 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 18:15:31 | ||
图片预览








文档简介
(共28张PPT)
高中数学 一年级
10.3 频率与概率
我们知道,事件的概率越大,意味着事件发生的可能性越大,在重复试验中,相应的频率一般也越大;事件的概率越小,则事件发生的可能性越小,在重复试验中,相应的频率一般也越小.在初中,我们利用频率与概率的这种关系,通过大量重复试验,用频率去估计概率.那么,在重复试验中,频率的大小是否就决定了概率的大小呢?频率与概率之间到底是一种怎样的关系呢?
一.复习旧知
1.频率:在相同的条件下,进行了次试验,在这次试验中,事件发生的次数称为事件发生的频数。比值称为事件A发生的频率,并记成
2.概率:对随机事件发生可能性大小的度量(数值)称为事件的概率,事件A的概率用P(A)表示。
二.探究
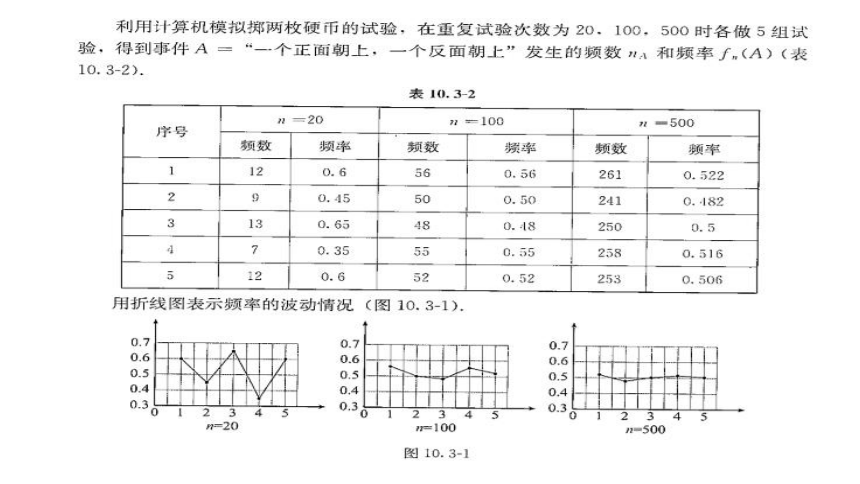
重复做同时抛掷两枚质地均匀的硬币实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你能发现什么规律?
把硬币正面朝上记为1,反面朝上记为0,则这个试验的样本空间Ω=,,所以
我们发现:
(1) 试验次数相同,频率可能不同,这说明随机事件发生的频率具有随机性。
(2)从整体来看,频率在概率0.5附近波动。当试验次数较少时,波动幅度较大;当试验次数较大时,波动幅度较小。但试验次数多的波动幅度并不全都比次数少的小,只是波动幅度小的可能性更大。
三.新知梳理
大量试验表明,在任何确定次数的随机试验中,一个随机事件A发生的频率具有随机性。
1.频率的稳定性
一般地,随着试验次数的增大,频率偏离概率的幅度会缩小,即事件发生的频率会逐渐稳定于事件发生的概率,我们称频率的这个性质为频率的稳定性.
2.频率稳定性的作用
可以用频率估计概率.
3.频率与概率的区别与联系
频率 概率
区别 本身是随机的观测值(试验值),在试验前无法确定,多数会随着试验的改变而变化,做同样次数的重复试验,得到的结果也会不同 本身是固定的理论值,与试验次数无关,只与事件自身的属性有关
联系 频率是概率的试验值,会随试验次数的增大逐渐稳定;概率是频率理论上的稳定值,在实际中可用频率估计概率 四.典例分析
题型一 频率和概率意义的理解
[典例1] 下列说法中正确的有( )
①任何事件的概率总是在[0,1]之间;
②概率是随机的,在试验前不能确定;
③频率是客观存在的,与试验次数无关;
④频率是概率的近似值,概率是频率的稳定值.
A.①④ B.②③
C.①③④ D.①②③④
[解析] 频率是不能脱离试验次数的实验值,而概率是具有确定性的不依赖于试验次数的理论值,故②③不正确.①④显然正确.
[答案] A
题型二 频率估计概率
时间范围 1年内 2年内 3年内 4年内
新生婴儿数n 5544 9607 13520 17190
男婴数m 2883 4970 6994 8892
[典例2]一个地区从某年起几年之内的新生婴儿数及其中的男婴数如下表所示:
(1)计算男婴的出生频率(保留4位小数);
(2)这一地区男婴出生的概率约是多少?
解(1)计算即得男婴出生的频率依次约为0.5200,0.5173,0.5173,0.5173.
(2)因为这些频率非常接近0.5173,所以这一地区男婴出生的概率约为0.5173.
反思感悟:由统计定义求概率的一般步骤
(1)确定随机事件A的频数nA;
(2)由计算频率fn(A)(n为试验的总次数)
(3)由频率fn(A)估计概率P(A).
概率可看成频率在理论上的稳定值,它从数量上反映了随机事件发生的可能性的大小,它是频率的科学抽象,当试验次数越来越多时频率向概率靠近,只要次数足够多,所得频率就近似地当作随机事件的概率.
题型三 用样本的频率估计总体的概率
[典例3]为了估计水库中鱼的尾数,可以使用以下的方法:先从水库中捕出一定数量的鱼,例如2 000尾,给每尾鱼做上记号,不影响其存活,然后放回水库.经过适当的时间,让其和水库中的其他鱼充分混合,再从水库中捕出一定数量的鱼,例如500尾,查看其中带记号的鱼,假设有40尾,根据上述数据,估计水库中鱼的尾数为 .
【解题提示】求2 000尾鱼占水库中所有鱼的百分比→
求带记号的鱼在500尾鱼中占的百分比→
根据二者的关系列等式→求解,估计水库中鱼的尾数
【解析】 设水库中鱼的尾数是n(n∈N+),现在要估计n的值,假设每尾鱼被捕到的可能性是相等的,从水库中任捕一尾鱼,记事件A={捕到带记号的鱼},则P(A)= .
第二次从水库中捕出500尾鱼,其中带记号的有40尾,即事件A发生的频数为40,由概率的统计定义知P(A)≈ ,即 ≈ ,解得n≈25000.
所以估计水库中的鱼有25000尾.
【答案】 25000
反思与感悟:
为什么用样本频率估计总体概率?
用样本频率值估计概率往往能快速且正确,但必须是抽取的样本有代表性,否则不可以.生活和生产实践中都是这样使用概率.没有必要对总体作统计,而且有些统计在试验的过程中是有破坏性的,例如统计一批灯泡的使用寿命,如果对总体全作了试验和统计,得出的使用寿命就没有应用价值了.
本题用样本频率作为总体频率,体现了用样本估计总体的思想,现实生活中是很有必要的.
题型四 游戏的公平性
[典例4] 某校高二年级(1)(2)班准备联合举行晚会,组织者欲使晚会气氛热烈、有趣,策划整场晚会以转盘游戏的方式进行,每个节目开始时,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.(1)班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时(1)班代表获胜,否则(2)班代表获胜.该方案对双方是否公平?为什么?
【解】 该方案是公平的,理由如下
各种情况如表所示:
4 5 6 7
1 5 6 7 8
2 6 7 8 9
3 7 8 9 10
(1)班由表可知该游戏可能出现的情况共有12种,其中两数字之和为偶数的有6种,为奇数的也有6种,所以(1)班代表获胜的概率P1==,(2)班代表获胜的概率P2= = ,即P1=P2,机会是均等的,所以该方案对双方是公平的.
用频率估计概率时,需要做大量的重复试验,并且有些试验还无法进行,因而我们可以根据不同的随机试验构建相应的随机数模拟实验,这样就可以快速地进行大量重复试验了
我们称利用随机模拟解决问题的方法为蒙特卡洛(Monte Carlo)方法。
产生随机数的方法:
(1)抽签法
(2)利用计算器或者计算机软件产生随机数。
注意:计算器或计算机产生的随机数是按照确定的算法产生的数,具有周期性(周期很长),他们具有类似随机数的性质。因此,计算器或计算机产生的随机数不是真正的随机数,我们称它们为伪随机数。
题型5 利用随机模拟计算概率
[典例5] 从你所在班级任意选出6名同学,调查他们的出生月份,假设出生在一月,二月……十二月是等可能的。设事件A=“至少有两人出生月份相同”,设计一种实验方法,模拟20次,估计事件A发生的概率。
方法1 构建如下有放回摸球试验进行模拟,在袋子中装入编号为1,2……12的12个球, 这些球除编号外没有什么差别,有放回的随机从袋中摸6次球,得到6个数代表6个人的出生月份,这就完成了一次模拟试验,如果这6个数中至少有2个相同,表示事件A发生了,重复以上模拟试验20次,就可以统计出事件A发生的频率。
抽签法
计算机产生随机数
课堂总结
1 .随机试验中,事件A发生的次数叫频数,频数除以试
验的次数叫做事件A发生的频率。
2 .频率是通过试验计算出来的结果,是不稳定的,通过
很多次试验总结出来的频率可以估计概率。
3 .很多事件发生的概率是不知道的,我们在使用其概率
时都使用频率代替。
4.有些试验的结果可以用随机数模拟产生,随机数模拟省
时省力,是预测和决策的重要方法。
5.随机数产生
谢谢观看
高中数学 一年级
10.3 频率与概率
我们知道,事件的概率越大,意味着事件发生的可能性越大,在重复试验中,相应的频率一般也越大;事件的概率越小,则事件发生的可能性越小,在重复试验中,相应的频率一般也越小.在初中,我们利用频率与概率的这种关系,通过大量重复试验,用频率去估计概率.那么,在重复试验中,频率的大小是否就决定了概率的大小呢?频率与概率之间到底是一种怎样的关系呢?
一.复习旧知
1.频率:在相同的条件下,进行了次试验,在这次试验中,事件发生的次数称为事件发生的频数。比值称为事件A发生的频率,并记成
2.概率:对随机事件发生可能性大小的度量(数值)称为事件的概率,事件A的概率用P(A)表示。
二.探究
重复做同时抛掷两枚质地均匀的硬币实验,设事件A=“一个正面朝上,一个反面朝上”,统计A出现的次数并计算频率,再与其概率进行比较,你能发现什么规律?
把硬币正面朝上记为1,反面朝上记为0,则这个试验的样本空间Ω=,,所以
我们发现:
(1) 试验次数相同,频率可能不同,这说明随机事件发生的频率具有随机性。
(2)从整体来看,频率在概率0.5附近波动。当试验次数较少时,波动幅度较大;当试验次数较大时,波动幅度较小。但试验次数多的波动幅度并不全都比次数少的小,只是波动幅度小的可能性更大。
三.新知梳理
大量试验表明,在任何确定次数的随机试验中,一个随机事件A发生的频率具有随机性。
1.频率的稳定性
一般地,随着试验次数的增大,频率偏离概率的幅度会缩小,即事件发生的频率会逐渐稳定于事件发生的概率,我们称频率的这个性质为频率的稳定性.
2.频率稳定性的作用
可以用频率估计概率.
3.频率与概率的区别与联系
频率 概率
区别 本身是随机的观测值(试验值),在试验前无法确定,多数会随着试验的改变而变化,做同样次数的重复试验,得到的结果也会不同 本身是固定的理论值,与试验次数无关,只与事件自身的属性有关
联系 频率是概率的试验值,会随试验次数的增大逐渐稳定;概率是频率理论上的稳定值,在实际中可用频率估计概率 四.典例分析
题型一 频率和概率意义的理解
[典例1] 下列说法中正确的有( )
①任何事件的概率总是在[0,1]之间;
②概率是随机的,在试验前不能确定;
③频率是客观存在的,与试验次数无关;
④频率是概率的近似值,概率是频率的稳定值.
A.①④ B.②③
C.①③④ D.①②③④
[解析] 频率是不能脱离试验次数的实验值,而概率是具有确定性的不依赖于试验次数的理论值,故②③不正确.①④显然正确.
[答案] A
题型二 频率估计概率
时间范围 1年内 2年内 3年内 4年内
新生婴儿数n 5544 9607 13520 17190
男婴数m 2883 4970 6994 8892
[典例2]一个地区从某年起几年之内的新生婴儿数及其中的男婴数如下表所示:
(1)计算男婴的出生频率(保留4位小数);
(2)这一地区男婴出生的概率约是多少?
解(1)计算即得男婴出生的频率依次约为0.5200,0.5173,0.5173,0.5173.
(2)因为这些频率非常接近0.5173,所以这一地区男婴出生的概率约为0.5173.
反思感悟:由统计定义求概率的一般步骤
(1)确定随机事件A的频数nA;
(2)由计算频率fn(A)(n为试验的总次数)
(3)由频率fn(A)估计概率P(A).
概率可看成频率在理论上的稳定值,它从数量上反映了随机事件发生的可能性的大小,它是频率的科学抽象,当试验次数越来越多时频率向概率靠近,只要次数足够多,所得频率就近似地当作随机事件的概率.
题型三 用样本的频率估计总体的概率
[典例3]为了估计水库中鱼的尾数,可以使用以下的方法:先从水库中捕出一定数量的鱼,例如2 000尾,给每尾鱼做上记号,不影响其存活,然后放回水库.经过适当的时间,让其和水库中的其他鱼充分混合,再从水库中捕出一定数量的鱼,例如500尾,查看其中带记号的鱼,假设有40尾,根据上述数据,估计水库中鱼的尾数为 .
【解题提示】求2 000尾鱼占水库中所有鱼的百分比→
求带记号的鱼在500尾鱼中占的百分比→
根据二者的关系列等式→求解,估计水库中鱼的尾数
【解析】 设水库中鱼的尾数是n(n∈N+),现在要估计n的值,假设每尾鱼被捕到的可能性是相等的,从水库中任捕一尾鱼,记事件A={捕到带记号的鱼},则P(A)= .
第二次从水库中捕出500尾鱼,其中带记号的有40尾,即事件A发生的频数为40,由概率的统计定义知P(A)≈ ,即 ≈ ,解得n≈25000.
所以估计水库中的鱼有25000尾.
【答案】 25000
反思与感悟:
为什么用样本频率估计总体概率?
用样本频率值估计概率往往能快速且正确,但必须是抽取的样本有代表性,否则不可以.生活和生产实践中都是这样使用概率.没有必要对总体作统计,而且有些统计在试验的过程中是有破坏性的,例如统计一批灯泡的使用寿命,如果对总体全作了试验和统计,得出的使用寿命就没有应用价值了.
本题用样本频率作为总体频率,体现了用样本估计总体的思想,现实生活中是很有必要的.
题型四 游戏的公平性
[典例4] 某校高二年级(1)(2)班准备联合举行晚会,组织者欲使晚会气氛热烈、有趣,策划整场晚会以转盘游戏的方式进行,每个节目开始时,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.(1)班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时(1)班代表获胜,否则(2)班代表获胜.该方案对双方是否公平?为什么?
【解】 该方案是公平的,理由如下
各种情况如表所示:
4 5 6 7
1 5 6 7 8
2 6 7 8 9
3 7 8 9 10
(1)班由表可知该游戏可能出现的情况共有12种,其中两数字之和为偶数的有6种,为奇数的也有6种,所以(1)班代表获胜的概率P1==,(2)班代表获胜的概率P2= = ,即P1=P2,机会是均等的,所以该方案对双方是公平的.
用频率估计概率时,需要做大量的重复试验,并且有些试验还无法进行,因而我们可以根据不同的随机试验构建相应的随机数模拟实验,这样就可以快速地进行大量重复试验了
我们称利用随机模拟解决问题的方法为蒙特卡洛(Monte Carlo)方法。
产生随机数的方法:
(1)抽签法
(2)利用计算器或者计算机软件产生随机数。
注意:计算器或计算机产生的随机数是按照确定的算法产生的数,具有周期性(周期很长),他们具有类似随机数的性质。因此,计算器或计算机产生的随机数不是真正的随机数,我们称它们为伪随机数。
题型5 利用随机模拟计算概率
[典例5] 从你所在班级任意选出6名同学,调查他们的出生月份,假设出生在一月,二月……十二月是等可能的。设事件A=“至少有两人出生月份相同”,设计一种实验方法,模拟20次,估计事件A发生的概率。
方法1 构建如下有放回摸球试验进行模拟,在袋子中装入编号为1,2……12的12个球, 这些球除编号外没有什么差别,有放回的随机从袋中摸6次球,得到6个数代表6个人的出生月份,这就完成了一次模拟试验,如果这6个数中至少有2个相同,表示事件A发生了,重复以上模拟试验20次,就可以统计出事件A发生的频率。
抽签法
计算机产生随机数
课堂总结
1 .随机试验中,事件A发生的次数叫频数,频数除以试
验的次数叫做事件A发生的频率。
2 .频率是通过试验计算出来的结果,是不稳定的,通过
很多次试验总结出来的频率可以估计概率。
3 .很多事件发生的概率是不知道的,我们在使用其概率
时都使用频率代替。
4.有些试验的结果可以用随机数模拟产生,随机数模拟省
时省力,是预测和决策的重要方法。
5.随机数产生
谢谢观看
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
