广东省深圳市福田区莲花中学2022-2023学年八年级下学期开学数学试卷(无答案)
文档属性
| 名称 | 广东省深圳市福田区莲花中学2022-2023学年八年级下学期开学数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 91.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 11:25:30 | ||
图片预览

文档简介
2022-2023学年广东省深圳市福田区莲花中学八年级(下)开学数学试卷
一、选择题(本题共10小题,每小题3分,共30分,每小题给出4个选项,其中只有一个是正确的)
1.下列各数中,无理数是( )
A.π B.3.14 C. D.
2.若点P(m,﹣2)在第三象限内,则m的值可以是( )
A.2 B.0 C.﹣2 D.±2
3.下列计算错误的是( )
A. B. C. D.
4.下列各组数中,不能作为直角三角形的三边的是( )
A.3,4,5 B.2,3, C.8,15,17 D.32,42,52
5.如图,△ABC是等边三角形,AE∥BF,若∠CAE=45°,则∠CBF的度数为( )
A.10° B.15° C.20° D.25°
6.某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
7.下列命题中,属于真命题的是( )
A.数轴上的每一个点都表示一个有理数
B.三角形的一个外角大于任一个内角
C.两直线平行,同旁内角相等
D.立方根等于它本身的实数有3个
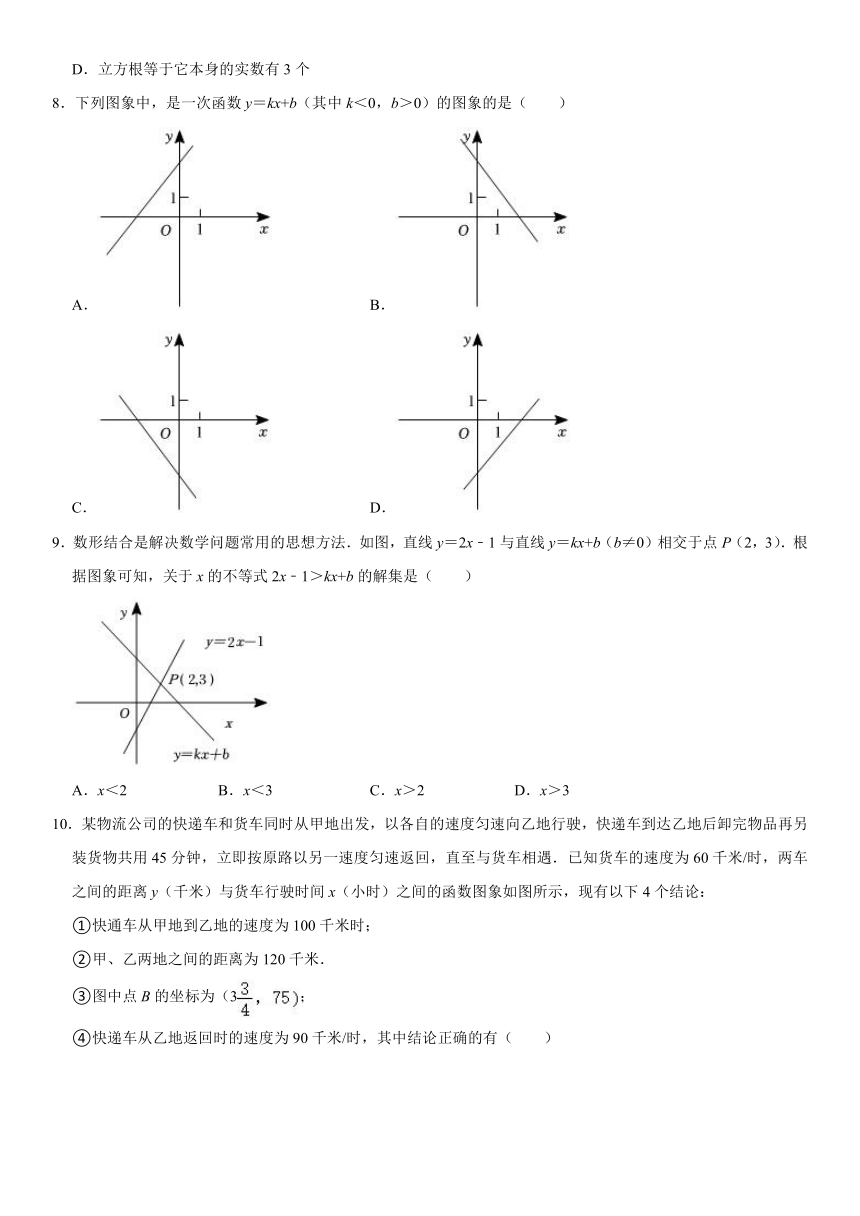
8.下列图象中,是一次函数y=kx+b(其中k<0,b>0)的图象的是( )
A. B.
C. D.
9.数形结合是解决数学问题常用的思想方法.如图,直线y=2x﹣1与直线y=kx+b(b≠0)相交于点P(2,3).根据图象可知,关于x的不等式2x﹣1>kx+b的解集是( )
A.x<2 B.x<3 C.x>2 D.x>3
10.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
①快通车从甲地到乙地的速度为100千米时;
②甲、乙两地之间的距离为120千米.
③图中点B的坐标为(3;
④快递车从乙地返回时的速度为90千米/时,其中结论正确的有( )
A.①②③④ B.①③④ C.①③ D.①②④
二、填空题(本题共5小题,每小题3分,共15分)
11.16的平方根是 .
12.点P(4,﹣2)到y轴的距离是 .
13.若一次函数y=kx+3与正比例函数y=2x的图象交于点(1,m),则方程组的解为 .
14.某商场搞优惠活动,凡在本商场一次性购买商品超过100元者,超过100元的部分按8折优惠.活动中,小明到该商场一次性购买单价为60元的礼盒x(x>2)件,则应付款y(元)与商品数x(件)之间的关系式,化简后的结果是 .
15.如图,直线y=﹣x+4与x轴交于点B,与y轴交于点C,点E(1,0),D为线段BC的中点,P为y轴上的一个动点,连接PD、PE,当△PED的周长最小时,点P的坐标为 .
三、解答题(本题共7小题,其中16题8分,17题6分,18,19,20,21题各8分,22题9分,共55分)
16.(1)计算:(+)×+;
(2)解方程组:.
17.解不等式组并将解集在数轴上表示出来.
18.为响应“双减”政策,老师们都精心设计每天的作业,兴华学校调查了部分学生每天完成作业所用时间,并用得到的数据绘制了如下不完整的统计图,根据图中信息完成下列问题:
(1)将条形统计图补充完整;
(2)抽查学生完成作业所用时间的众数是 ;
(3)求所有被抽查学生完成作业所用的平均时间.
19.如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求解答下列问题:
(1)在图中建立正确的平面直角坐标系,点B和点C的坐标分别
为 , ;
(2)作出△ABC关于x轴的对称图形△A'B'C'.(不要求写作法)
(3)BC的长度为 .
20.如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得EF=ED,连CF.
(1)求证:CF∥AB;
(2)若∠ABC=50°,连接BE,BE平分∠ABC,AC平分∠BCF,求∠A的度数.
21.幸福超市购进A、B两种饮料共200箱,两种饮料的成本与销售价如下表:
饮料 成本(元/箱) 销售价(元/箱)
A 25 35
B 35 50
(1)若该超市花了6500元进货,求购进A、B两种饮料各多少箱?
(2)设购进A种饮料a箱(50≤a≤100),200箱饮料全部卖完可获利润W元,求W与a的函数关系式,并求购进A种饮料多少箱时,可获得最大利润,最大利润是多少?
22.如图,在平面直角坐标系中,直线l1:y=x与直线l2:y=kx+b相交于点A(a,3),直线交l2交y轴于点B(0,﹣5).
(1)求直线l2的解析式;
(2)将△OAB沿直线l2翻折得到△CAB(其中点O的对应点为点C),求证AC∥OB;
(3)在直线BC下方以BC为边作等腰直角三角形BCP,直接写出点P的坐标.
一、选择题(本题共10小题,每小题3分,共30分,每小题给出4个选项,其中只有一个是正确的)
1.下列各数中,无理数是( )
A.π B.3.14 C. D.
2.若点P(m,﹣2)在第三象限内,则m的值可以是( )
A.2 B.0 C.﹣2 D.±2
3.下列计算错误的是( )
A. B. C. D.
4.下列各组数中,不能作为直角三角形的三边的是( )
A.3,4,5 B.2,3, C.8,15,17 D.32,42,52
5.如图,△ABC是等边三角形,AE∥BF,若∠CAE=45°,则∠CBF的度数为( )
A.10° B.15° C.20° D.25°
6.某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
7.下列命题中,属于真命题的是( )
A.数轴上的每一个点都表示一个有理数
B.三角形的一个外角大于任一个内角
C.两直线平行,同旁内角相等
D.立方根等于它本身的实数有3个
8.下列图象中,是一次函数y=kx+b(其中k<0,b>0)的图象的是( )
A. B.
C. D.
9.数形结合是解决数学问题常用的思想方法.如图,直线y=2x﹣1与直线y=kx+b(b≠0)相交于点P(2,3).根据图象可知,关于x的不等式2x﹣1>kx+b的解集是( )
A.x<2 B.x<3 C.x>2 D.x>3
10.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
①快通车从甲地到乙地的速度为100千米时;
②甲、乙两地之间的距离为120千米.
③图中点B的坐标为(3;
④快递车从乙地返回时的速度为90千米/时,其中结论正确的有( )
A.①②③④ B.①③④ C.①③ D.①②④
二、填空题(本题共5小题,每小题3分,共15分)
11.16的平方根是 .
12.点P(4,﹣2)到y轴的距离是 .
13.若一次函数y=kx+3与正比例函数y=2x的图象交于点(1,m),则方程组的解为 .
14.某商场搞优惠活动,凡在本商场一次性购买商品超过100元者,超过100元的部分按8折优惠.活动中,小明到该商场一次性购买单价为60元的礼盒x(x>2)件,则应付款y(元)与商品数x(件)之间的关系式,化简后的结果是 .
15.如图,直线y=﹣x+4与x轴交于点B,与y轴交于点C,点E(1,0),D为线段BC的中点,P为y轴上的一个动点,连接PD、PE,当△PED的周长最小时,点P的坐标为 .
三、解答题(本题共7小题,其中16题8分,17题6分,18,19,20,21题各8分,22题9分,共55分)
16.(1)计算:(+)×+;
(2)解方程组:.
17.解不等式组并将解集在数轴上表示出来.
18.为响应“双减”政策,老师们都精心设计每天的作业,兴华学校调查了部分学生每天完成作业所用时间,并用得到的数据绘制了如下不完整的统计图,根据图中信息完成下列问题:
(1)将条形统计图补充完整;
(2)抽查学生完成作业所用时间的众数是 ;
(3)求所有被抽查学生完成作业所用的平均时间.
19.如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求解答下列问题:
(1)在图中建立正确的平面直角坐标系,点B和点C的坐标分别
为 , ;
(2)作出△ABC关于x轴的对称图形△A'B'C'.(不要求写作法)
(3)BC的长度为 .
20.如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得EF=ED,连CF.
(1)求证:CF∥AB;
(2)若∠ABC=50°,连接BE,BE平分∠ABC,AC平分∠BCF,求∠A的度数.
21.幸福超市购进A、B两种饮料共200箱,两种饮料的成本与销售价如下表:
饮料 成本(元/箱) 销售价(元/箱)
A 25 35
B 35 50
(1)若该超市花了6500元进货,求购进A、B两种饮料各多少箱?
(2)设购进A种饮料a箱(50≤a≤100),200箱饮料全部卖完可获利润W元,求W与a的函数关系式,并求购进A种饮料多少箱时,可获得最大利润,最大利润是多少?
22.如图,在平面直角坐标系中,直线l1:y=x与直线l2:y=kx+b相交于点A(a,3),直线交l2交y轴于点B(0,﹣5).
(1)求直线l2的解析式;
(2)将△OAB沿直线l2翻折得到△CAB(其中点O的对应点为点C),求证AC∥OB;
(3)在直线BC下方以BC为边作等腰直角三角形BCP,直接写出点P的坐标.
同课章节目录
