第五单元组合图形的面积(课件)五年级上册数学沪教版(共17张PPT)
文档属性
| 名称 | 第五单元组合图形的面积(课件)五年级上册数学沪教版(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 21:59:18 | ||
图片预览


文档简介
(共17张PPT)
组合图形的面积
a
a
b
a
a
h
a
a
b
a
a
h
a
h
a
h
h
b
a
h
b
a
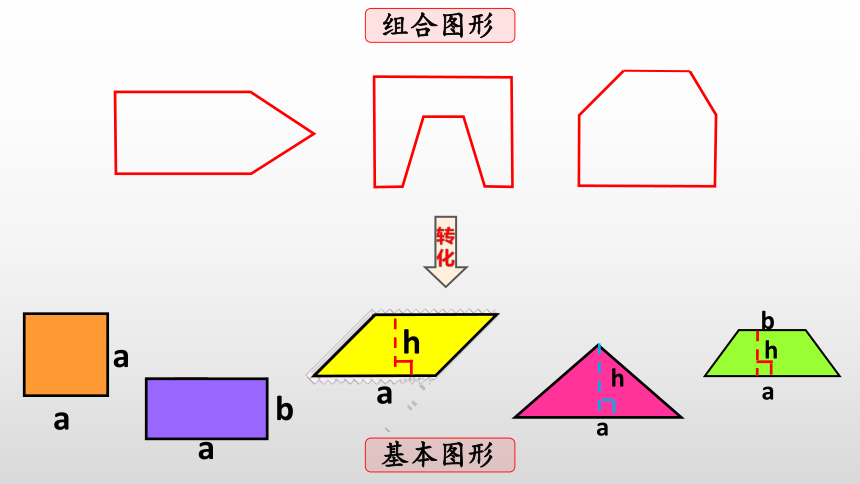
基本图形
a
h
a
a
b
a
a
h
h
b
a
基本图形
组合图形
转化
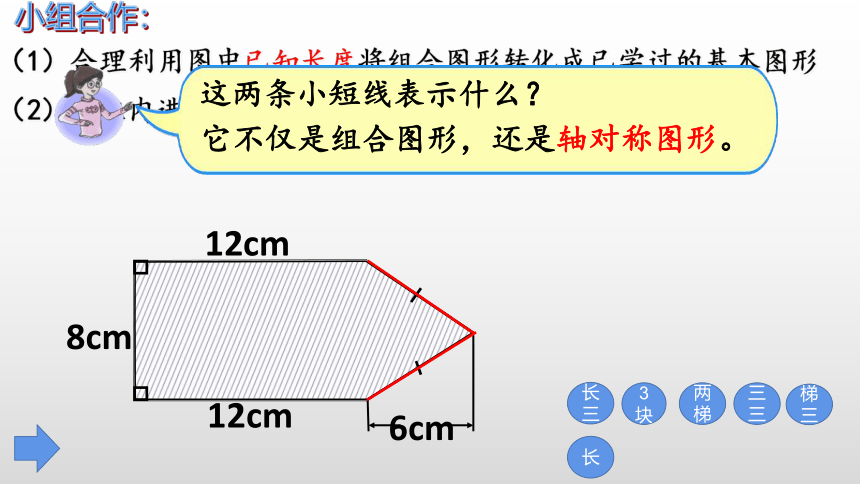
小组合作:
(1)合理利用图中已知长度将组合图形转化成已学过的基本图形
(2)在组内进行交流:你转化成了哪些基本图形?
这些图形的边分别有多长?
长
三
两
梯
长
三
三
梯三
12cm
8cm
6cm
12cm
3块
这两条小短线表示什么?
它不仅是组合图形,还是轴对称图形。
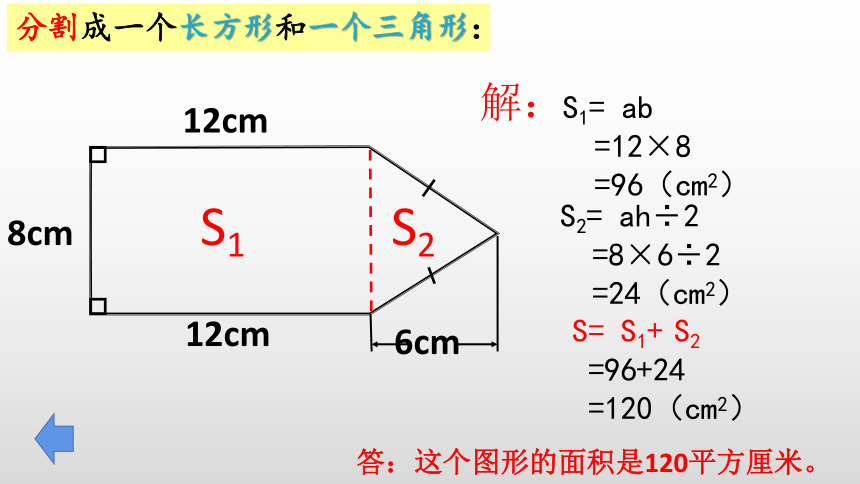
分割成一个长方形和一个三角形:
S1= ab
=12×8
=96(cm2)
S2= ah÷2
=8×6÷2
=24(cm2)
S= S1+ S2
=96+24
=120(cm2)
解:
答:这个图形的面积是120平方厘米。
S1
S2
12cm
8cm
6cm
12cm
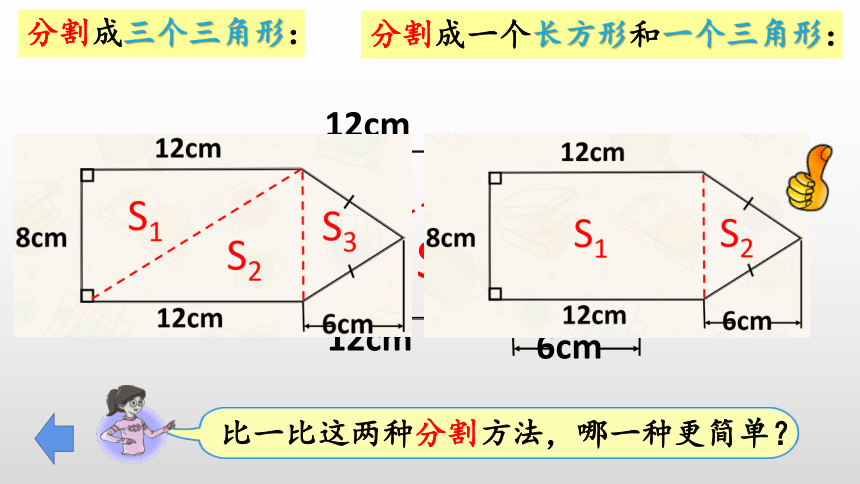
分割成三个三角形:
S1
S2
12cm
8cm
6cm
12cm
S3
分割成一个长方形和一个三角形:
比一比这两种分割方法,哪一种更简单?
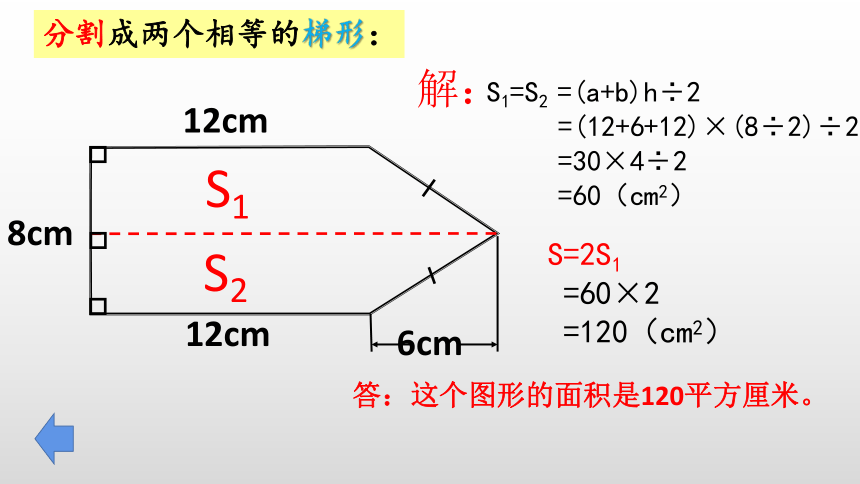
分割成两个相等的梯形:
解:
答:这个图形的面积是120平方厘米。
S1=S2 =(a+b)h÷2
=(12+6+12)×(8÷2)÷2
=30×4÷2
=60(cm2)
S=2S1
=60×2
=120(cm2)
12cm
8cm
6cm
12cm
S1
S2
12cm
8cm
6cm
S1= ah÷2
=8×(12+6)÷2
=72(cm2)
S1
S2
S2= S3= ah÷2
=12×(8÷2)÷2
=24(cm2)
S= S1+ S2+S3
=72+24+24
=120(cm2)
解:
答:这个图形的面积是120平方厘米。
12cm
S3
分割成三个三角形:
12cm
8cm
6cm
12cm
分割成两个梯形:
能不能找到这些图形的边长?
12cm
8cm
6cm
S长= ab
=(12+6) ×8
=18×8
=144(cm2)
S1
S2
S= S长-S1- S2
=144-12-12
=120(cm2)
S1=S2 =ah÷2
=6× (8÷2)÷2
=6×4÷2
=12(cm2)
解:
答:这个图形的面积是120平方厘米。
S长
拼补成一个长方形:
对比求组合图形面积的方法
观察图形特点
观察已知数据
让计算简洁
分割
求和
拼补
求差
哪种方法更简单?
求图形的面积。(单位:cm)
选择分割法还是拼补法?
分割法
拼补法
S1
S2
?
?
S2=(a+b)h÷2
=(3+5)×2÷2
=8(cm2)
解:
S1=ab
=5×3
=15(cm2)
S=S1+S2
=8+15
=23(cm2)
答:这个组合图形的面积是23cm2。
求图形的面积。(单位:cm) 书P73
没有直接给出数据
选择分割法还是拼补法?
分割法
拼补法
S1
?
?
S长=ab
=20×16
=320(cm2)
解:
S1=(a+b)h÷2
=(6+12)×10÷2
=18×10÷2
=90(cm2)
S=S长-S1
=320-90
=230(cm2)
答:这个组合图形的面积是230cm2。
梯形的下底:
20-2×4=12(cm)
判断:小丁丁求图形的面积计算正确吗?
错误。
延长后不是分割成了两个三角形。
S2=ah÷2
=(6-4)×(7-4)÷2
=2×3÷2
=3(cm2)
解:
S1=ab
=6×4
=24(cm2)
S=S1+S2
=24+3
=27(cm2)
答:这个组合图形的面积是27cm2。
下图是教室的一堵墙,如果砌这面墙每平方米用砖185块,一共需要多少块砖?
5m
4m
1.2m
S1
S2
S2=ah÷2
=5×1.2÷2
=6÷2
=3(m2)
解:
S1=ab
=5×4
=20(m2)
S=S1+S2
=20+3
=23(m2)
答:一共需要4255块砖。
23×185=4255(块)
下图有两个正方形,比较阴影部分的面积谁大?
S阴=S大长÷2
S2
S1
S2
S3
S阴=S大长÷2-S4
S1
S3
S4
>
对比求组合图形面积的方法
观察图形特点
观察已知数据
让计算简洁
分割
求和
拼补
求差
哪种方法更简单?
组合图形的面积
a
a
b
a
a
h
a
a
b
a
a
h
a
h
a
h
h
b
a
h
b
a
基本图形
a
h
a
a
b
a
a
h
h
b
a
基本图形
组合图形
转化
小组合作:
(1)合理利用图中已知长度将组合图形转化成已学过的基本图形
(2)在组内进行交流:你转化成了哪些基本图形?
这些图形的边分别有多长?
长
三
两
梯
长
三
三
梯三
12cm
8cm
6cm
12cm
3块
这两条小短线表示什么?
它不仅是组合图形,还是轴对称图形。
分割成一个长方形和一个三角形:
S1= ab
=12×8
=96(cm2)
S2= ah÷2
=8×6÷2
=24(cm2)
S= S1+ S2
=96+24
=120(cm2)
解:
答:这个图形的面积是120平方厘米。
S1
S2
12cm
8cm
6cm
12cm
分割成三个三角形:
S1
S2
12cm
8cm
6cm
12cm
S3
分割成一个长方形和一个三角形:
比一比这两种分割方法,哪一种更简单?
分割成两个相等的梯形:
解:
答:这个图形的面积是120平方厘米。
S1=S2 =(a+b)h÷2
=(12+6+12)×(8÷2)÷2
=30×4÷2
=60(cm2)
S=2S1
=60×2
=120(cm2)
12cm
8cm
6cm
12cm
S1
S2
12cm
8cm
6cm
S1= ah÷2
=8×(12+6)÷2
=72(cm2)
S1
S2
S2= S3= ah÷2
=12×(8÷2)÷2
=24(cm2)
S= S1+ S2+S3
=72+24+24
=120(cm2)
解:
答:这个图形的面积是120平方厘米。
12cm
S3
分割成三个三角形:
12cm
8cm
6cm
12cm
分割成两个梯形:
能不能找到这些图形的边长?
12cm
8cm
6cm
S长= ab
=(12+6) ×8
=18×8
=144(cm2)
S1
S2
S= S长-S1- S2
=144-12-12
=120(cm2)
S1=S2 =ah÷2
=6× (8÷2)÷2
=6×4÷2
=12(cm2)
解:
答:这个图形的面积是120平方厘米。
S长
拼补成一个长方形:
对比求组合图形面积的方法
观察图形特点
观察已知数据
让计算简洁
分割
求和
拼补
求差
哪种方法更简单?
求图形的面积。(单位:cm)
选择分割法还是拼补法?
分割法
拼补法
S1
S2
?
?
S2=(a+b)h÷2
=(3+5)×2÷2
=8(cm2)
解:
S1=ab
=5×3
=15(cm2)
S=S1+S2
=8+15
=23(cm2)
答:这个组合图形的面积是23cm2。
求图形的面积。(单位:cm) 书P73
没有直接给出数据
选择分割法还是拼补法?
分割法
拼补法
S1
?
?
S长=ab
=20×16
=320(cm2)
解:
S1=(a+b)h÷2
=(6+12)×10÷2
=18×10÷2
=90(cm2)
S=S长-S1
=320-90
=230(cm2)
答:这个组合图形的面积是230cm2。
梯形的下底:
20-2×4=12(cm)
判断:小丁丁求图形的面积计算正确吗?
错误。
延长后不是分割成了两个三角形。
S2=ah÷2
=(6-4)×(7-4)÷2
=2×3÷2
=3(cm2)
解:
S1=ab
=6×4
=24(cm2)
S=S1+S2
=24+3
=27(cm2)
答:这个组合图形的面积是27cm2。
下图是教室的一堵墙,如果砌这面墙每平方米用砖185块,一共需要多少块砖?
5m
4m
1.2m
S1
S2
S2=ah÷2
=5×1.2÷2
=6÷2
=3(m2)
解:
S1=ab
=5×4
=20(m2)
S=S1+S2
=20+3
=23(m2)
答:一共需要4255块砖。
23×185=4255(块)
下图有两个正方形,比较阴影部分的面积谁大?
S阴=S大长÷2
S2
S1
S2
S3
S阴=S大长÷2-S4
S1
S3
S4
>
对比求组合图形面积的方法
观察图形特点
观察已知数据
让计算简洁
分割
求和
拼补
求差
哪种方法更简单?
同课章节目录
