切线的判定

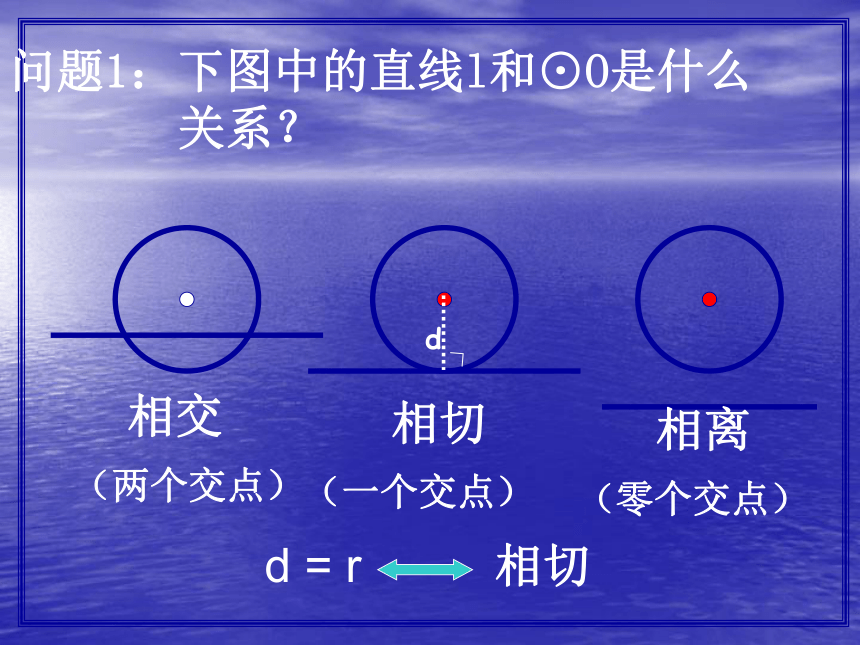
课件14张PPT。切线的判定24.2.2(第二课时）问题1：下图中的直线l和⊙O是什么
关系？相交相离相切（两个交点）（一个交点）（零个交点）d = r
相切d∟问题2:如图，已知点A是⊙O上一点，
过A作OA的垂线l，这样的直线有几
条？ 直线l与⊙O的位置关系怎样？
为什么？lAOdr特征一：直线l经过半径OA
的外端点A特征二：直线l垂直于半径OAd = r
相切切线的判定定理：经过半径外端
并且垂直于这条半径的直线是圆
的切线。判断下图直线l是否是⊙O的切线？
并说明为什么。证明一条直线为圆的切线时，必须两个条件缺一不可：①过半径外端
②垂直于这条半径。 已知：直线AB经过⊙O上的
点C，并且OA=OB,CA=CB.
求证：直线AB是⊙O的切线。OABC分析： 欲证AB是⊙O的切线，由于AB过圆上点C，若连结OC,则AB过半径OC的外端，只需证明OC⊥AB .例1例1、已知：直线AB经过⊙O上的
点C，并且OA=OB,CA=CB.
求证：直线AB是⊙O的切线。OABC证明：如图，连结OC.
∵ OA=OB,CA=CB
∴ OC是等腰△OAB
底边BC上的中线
∴ OC⊥AB
又AB过半径OC的外端
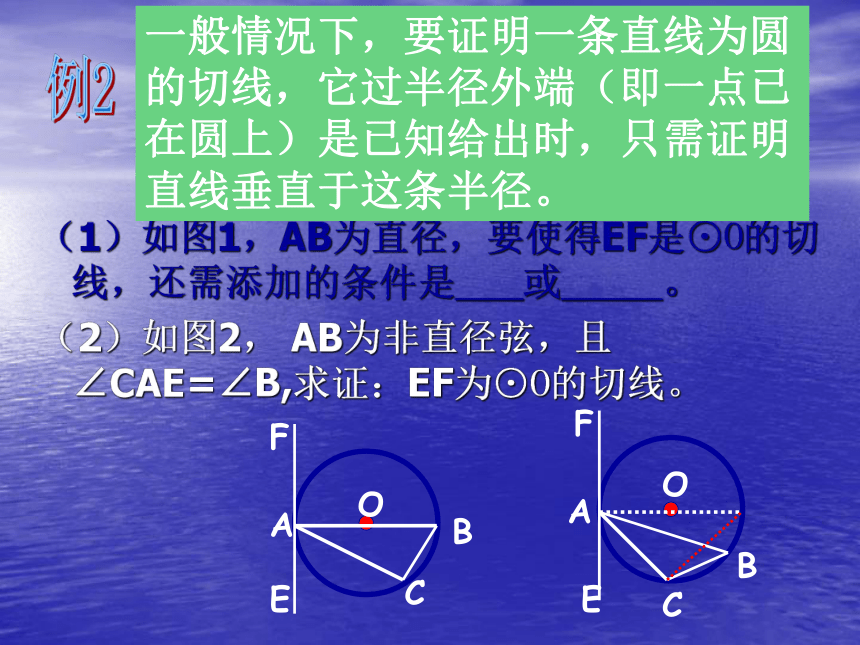
∴ AB是⊙O的切线已知△ABC内接于⊙O,直线EF过点A（1）如图1，AB为直径，要使得EF是⊙O的切线，还需添加的条件是 或 。
（2）如图2， AB为非直径弦，且∠CAE=∠B,求证：EF为⊙O的切线。例2一般情况下，要证明一条直线为圆的切线，它过半径外端（即一点已在圆上）是已知给出时，只需证明直线垂直于这条半径。练习１：
AB是⊙O的直径，点D在AB的延长线上
BD=OB,点C在圆上，∠CAB=30°。
求证：DC是⊙O的切线。CDBAO已知O为∠BAC平分线上一点，OD⊥AB于D，以O为圆心，OD为半径作圆O，求证：⊙O与AC相切练习2：证明直线与圆相切，但无切点时，往往过圆心作切线的垂线，再证明d=r即可DCABO∟切线的判定方法有：③、切线的判定定理。②、直线到圆心的距离等于圆的半径。①、直线与圆有一个公共点。小结切线的判定定理：经过半径外端
并且垂直于这条半径的直线是圆
的切线。思考？改变切线判定定理的题设与结论
如果直线l是⊙O的切线，切点为A,那么半径OA与直线l是不是一定垂直呢？切线的性质定理：
圆的切线垂直于过切点的半径。AL1L2BO如图，AB是⊙O的直径，直线L1、L2
是⊙O的切线，A、B是切点,直线L1、L2有怎样的位置关系？
练习 ⑴、经过半径外端的直线是圆的切线。
⑵、垂直于半径的直线是圆的切线。
⑶、过直径的外端并且垂直于这条直径的
直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切
线。
⑸、以等腰三角形的顶点为圆心，底边上
的高为半径的圆与底边相切。
是非题：判断下列命题是否正确。（×）（×）（√）（√）（√）本节小结切线的判定定理：经过半径外端
并且垂直于这条半径的直线是圆
的切线。
切线的性质定理：
圆的切线垂直于过切点的半径。