有理数的加法(山东省济南市)
文档属性
| 名称 | 有理数的加法(山东省济南市) |

|
|
| 格式 | rar | ||
| 文件大小 | 724.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-08 00:00:00 | ||
图片预览




文档简介
课件15张PPT。有理数的加法运算一.复习提问
1、比较下列各对有理数的大小关系。
(1)7和4; (2)-7和4; (3)-3.5和-4; (4)-1/2和-2/3。
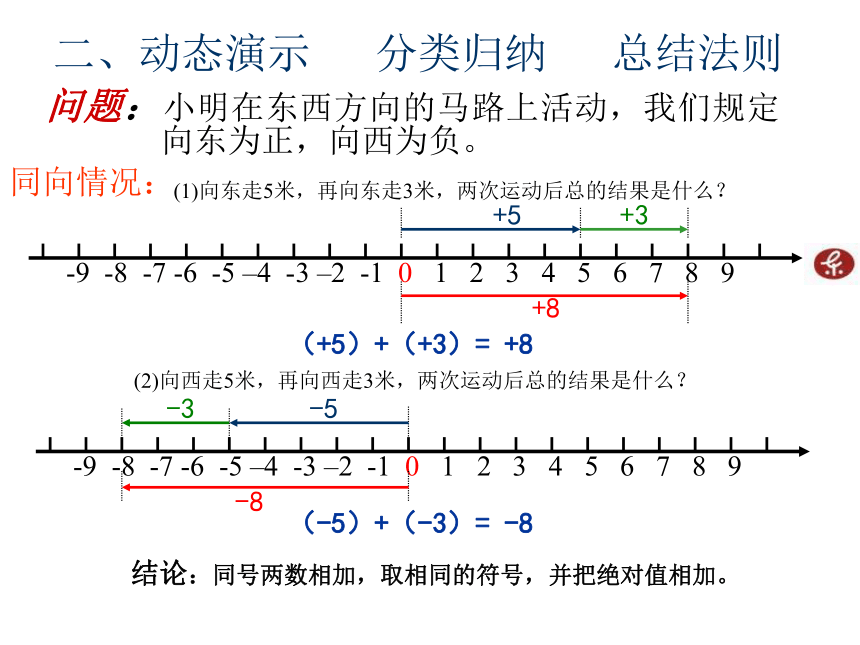
二、动态演示 分类归纳 总结法则问题:小明在东西方向的马路上活动,我们规定向东为正,向西为负。
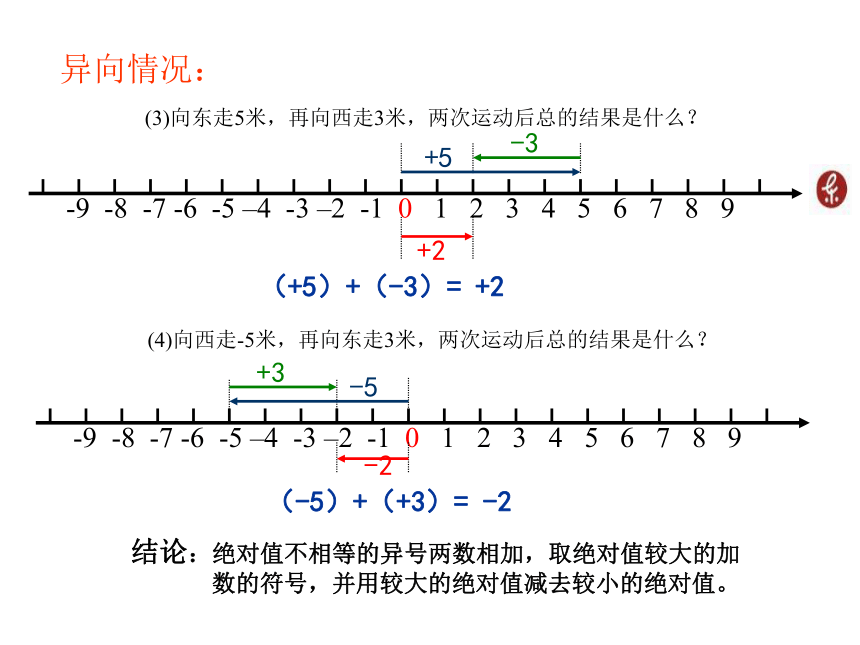
(1)向东走5米,再向东走3米,两次运动后总的结果是什么?+5+3+8(+5)+(+3)= +8 (2)向西走5米,再向西走3米,两次运动后总的结果是什么? 同向情况:-3-5-8(-5)+(-3)= -8 结论:同号两数相加,取相同的符号,并把绝对值相加。 异向情况:(3)向东走5米,再向西走3米,两次运动后总的结果是什么? +2(+5)+(-3)= +2 +5-3(4)向西走-5米,再向东走3米,两次运动后总的结果是什么? +3-5-2(-5)+(+3)= -2 结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。 问题:在东西走向的马路上,小明从O点出发,向东走5米,再向西走
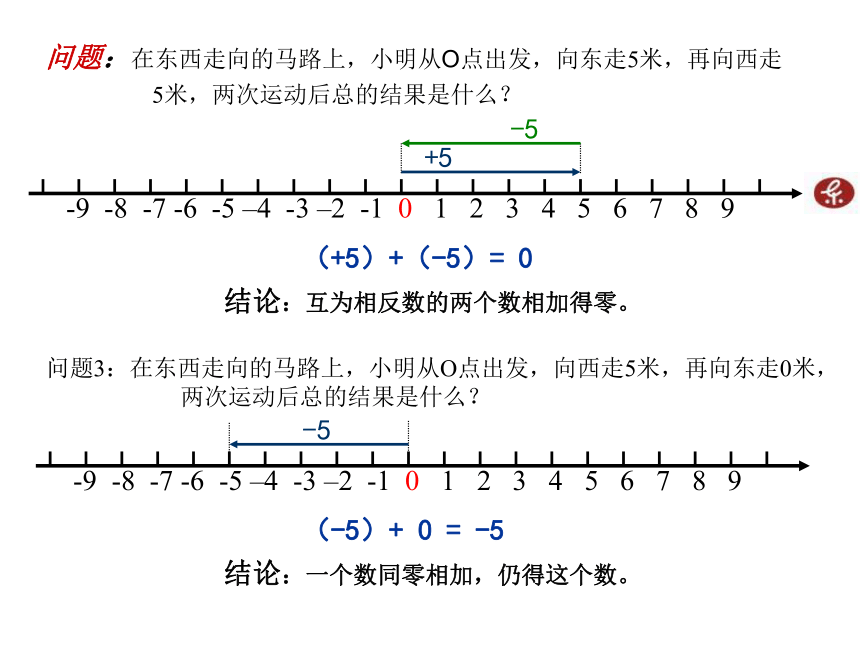
5米,两次运动后总的结果是什么? 问题3:在东西走向的马路上,小明从O点出发,向西走5米,再向东走0米,两次运动后总的结果是什么? (+5)+(-5)= 0 +5-5结论:互为相反数的两个数相加得零。 结论:一个数同零相加,仍得这个数。 -5(-5)+ 0 = -5 有理数加法法则
1.同号两数相加,取相同的符号,并把绝对值相加。
2.异号两数相加绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.
3.一个数同0相加,仍得这个数。有理数的加法法则:若a>0,b>0,则a+b=|a|+|b|;
若a<0,b<0,则a+b= -(|a|+|b|);
若a>0,b<0,|a|>|b|,则a+b=|a|+|b|;
若a>0,b<0, |a|<|b|,则a+b= -(|b| -|a|);
若a>0,b<0, |a|=|b|,则a+b= 0
{{同号两数相加异号两数相加三、强化理解 总结步骤 ( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓
同号两数相加 取相同符号 通过绝对值化归
为算术数的加法
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓
异号两数相加 取绝对值较大 通过绝对值化归
的加数的符号 为算术数的减法
四、例题讲解例1、计算。
(1)(-3)+(-9) (2)-4.7)+3.9解: (1)(-3)+(-9) = -(3+9)= -12
(2)-4.7)+3.9= -(4.7-3.9)= -0.8 例题、足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数。解:每个队的进球总数记为正数,失球总数记为负数,这两数和的和为这队的净胜球数。
红队: 4+( -2)=2
黄队:2+( -4)= -2
蓝队:1+( -1)=0(1) ( -6 ) + ( -8 ) ; (2) 5.2 + (- 4.5) ; (3) +五、巩固练习 1、 计算下列各题2、口算下列各题.
(1)(-4)+(-7); (2)(+4)+(-7);
(3)(-4)+(+7) ; (4)(+4)+(-4); ;
(5)(-9)+(+2); (6)(-9)+0六、拓展迁移1、若|a|=3|b|=2,且a、b异号,则a+b=( )
A、5 B、1 C、1或者-1 D、 5或者-5 2、若|a|+|b|=0,则a=( ),b=( )3、若a>0,b<0, |a|<|b|,则a+b( )0七、学有所思1、想一想:在有理数的加法运算中,和与加数有什么关系?
2、若|a -2|+|b+3|=0,则 a=( ),b=( )八、课时小结 这节课我们主要学习了有理数加法的运算法则,并熟练用运算进行计算。布置作业 书本第24页第一大题1、3、5、7四小题。
1、比较下列各对有理数的大小关系。
(1)7和4; (2)-7和4; (3)-3.5和-4; (4)-1/2和-2/3。
二、动态演示 分类归纳 总结法则问题:小明在东西方向的马路上活动,我们规定向东为正,向西为负。
(1)向东走5米,再向东走3米,两次运动后总的结果是什么?+5+3+8(+5)+(+3)= +8 (2)向西走5米,再向西走3米,两次运动后总的结果是什么? 同向情况:-3-5-8(-5)+(-3)= -8 结论:同号两数相加,取相同的符号,并把绝对值相加。 异向情况:(3)向东走5米,再向西走3米,两次运动后总的结果是什么? +2(+5)+(-3)= +2 +5-3(4)向西走-5米,再向东走3米,两次运动后总的结果是什么? +3-5-2(-5)+(+3)= -2 结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。 问题:在东西走向的马路上,小明从O点出发,向东走5米,再向西走
5米,两次运动后总的结果是什么? 问题3:在东西走向的马路上,小明从O点出发,向西走5米,再向东走0米,两次运动后总的结果是什么? (+5)+(-5)= 0 +5-5结论:互为相反数的两个数相加得零。 结论:一个数同零相加,仍得这个数。 -5(-5)+ 0 = -5 有理数加法法则
1.同号两数相加,取相同的符号,并把绝对值相加。
2.异号两数相加绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.
3.一个数同0相加,仍得这个数。有理数的加法法则:若a>0,b>0,则a+b=|a|+|b|;
若a<0,b<0,则a+b= -(|a|+|b|);
若a>0,b<0,|a|>|b|,则a+b=|a|+|b|;
若a>0,b<0, |a|<|b|,则a+b= -(|b| -|a|);
若a>0,b<0, |a|=|b|,则a+b= 0
{{同号两数相加异号两数相加三、强化理解 总结步骤 ( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓
同号两数相加 取相同符号 通过绝对值化归
为算术数的加法
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓
异号两数相加 取绝对值较大 通过绝对值化归
的加数的符号 为算术数的减法
四、例题讲解例1、计算。
(1)(-3)+(-9) (2)-4.7)+3.9解: (1)(-3)+(-9) = -(3+9)= -12
(2)-4.7)+3.9= -(4.7-3.9)= -0.8 例题、足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数。解:每个队的进球总数记为正数,失球总数记为负数,这两数和的和为这队的净胜球数。
红队: 4+( -2)=2
黄队:2+( -4)= -2
蓝队:1+( -1)=0(1) ( -6 ) + ( -8 ) ; (2) 5.2 + (- 4.5) ; (3) +五、巩固练习 1、 计算下列各题2、口算下列各题.
(1)(-4)+(-7); (2)(+4)+(-7);
(3)(-4)+(+7) ; (4)(+4)+(-4); ;
(5)(-9)+(+2); (6)(-9)+0六、拓展迁移1、若|a|=3|b|=2,且a、b异号,则a+b=( )
A、5 B、1 C、1或者-1 D、 5或者-5 2、若|a|+|b|=0,则a=( ),b=( )3、若a>0,b<0, |a|<|b|,则a+b( )0七、学有所思1、想一想:在有理数的加法运算中,和与加数有什么关系?
2、若|a -2|+|b+3|=0,则 a=( ),b=( )八、课时小结 这节课我们主要学习了有理数加法的运算法则,并熟练用运算进行计算。布置作业 书本第24页第一大题1、3、5、7四小题。
