中考数学《分类讨论思想》复习课件
图片预览




文档简介
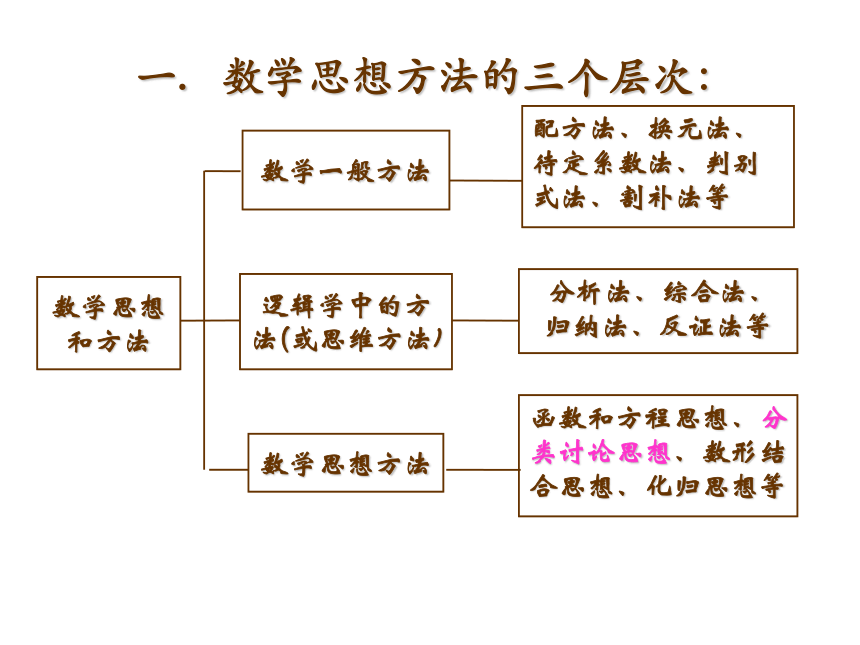
课件16张PPT。分类讨论思想中考专题复习之二一. 数学思想方法的三个层次: 分类讨论思想分类思想是根据数学本质属性的相同点和不同点,将数学研究对象分为不同种类的一种数学思想。分类以比较为基础,比较是分类的前提,分类是比较的结果。
分类必须有一定的标准,标准不同分类的结果也就不同。分类要做到不遗漏,不重复。分类后,对每个类进行研究,使问题在各种不同的情况下,分别得到各种结论,这就是讨论。分类讨论思想分类讨论是对问题深入研究的思想方法,用分类讨论的思想,有助于发现解题思路和掌握技能技巧,做到举一反三,触类旁通。
分类的思想随处可见,既有概念的分类:如实数、有理数、绝对值、点(直线、圆)与圆的位置关系和两圆相切等概念的分类;又有解题方法上的分类,如代数式中含有字母系数的方程、不等式;还有几何中图形位置关系不确定的分类,等腰三角形的顶角顶点不确定、相似三角形的对应关系不确定等。 zxxk 一.与概念有关的分类1. 一次函数y=kx+b的自变量的取值范围是
-3≤x≤ 6,,相应的函数值的取值范围是
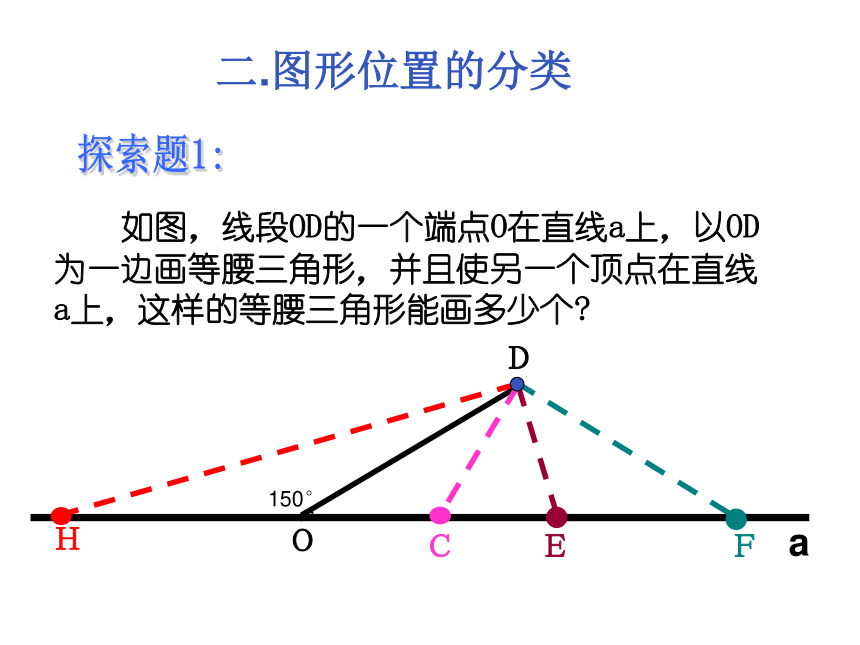
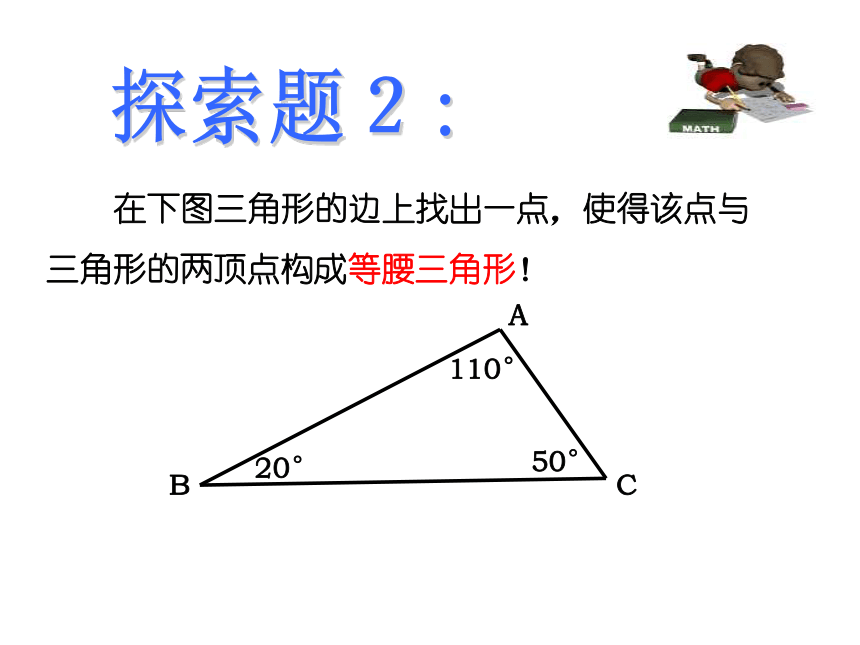
-5≤y≤-2 ,则这个函数的解析式 。解析式为 Y= x-4, 或 y=- x-3 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD150°⌒CaEFH探索题1:二.图形位置的分类探索题2: 在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论(分类讨论)3. 如图,直线AB经过圆O的圆心,与圆O交于A、B两点,点C在O上,且∠AOC=30度,点P是直线AB上的一个动点(与点O不重合),直线PC与圆O相交于点Q,问点P在直线AB的什么位置时,QP=QO?这样的点P有几个?并相应地求出∠OCP的度数。解:∵OQ=OC,OQ=OP ∴∠OQC=∠OCQ,∠QOP=∠QPO 设∠OCP=x度 , 则有:(2)如果点P在线段OB上,显然有PQ>OQ,所以点P不可能在线段OB上。(1)如上图, 当点P在线段OA上时, ∵∠OQC=∠OCP=x,
∴∠QPO=(180-∠OQP)=(180-x)
又∠QPO=∠OCP+∠COP,(180-x)=x+30,
解得x=40, 即∠OCP=40度(3)如图,当点P在的OA延长线上时,
∵∠OQC=∠OCQ=180-x,
∴∠OPQ= (180-x)= x.
又∵∠QCO=∠CPO+∠COP,∴180-x=x+30,
解得x=100 即∠OCP=100度(4)如图当P在OB的延长线上时,
∵∠OQC=∠OCQ=x,∴∠OQC=∠QPO+∠QOP,
∴∠QPO= ∠OQC= x,
又∠COA=∠OCP+∠CPO, 解方程30=x+ x,
得到x=20 即∠OCP=20度6。在Rt△ABC中,∠C=90,AC=3,BC=4。若以C为圆心,R为半径的圆与斜边只有一个公共点,则R的值为多少?4。在半径为1的圆O中,弦AB、AC的长分别是 ,
则∠BAC的度数是 。5。△ABC是半径为2cm的圆的内接三角形,
若BC=2 cm,则角A的度数是 。7..半径为R的两个等圆外切,则半径为2R且和这两个圆都相切的圆有几个?三.与相似三角形有关的分类8。在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动。如果P、Q同时出发,用t秒表示移动的时间(0<x<6)那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QAPC的面积;
提出一个与计算结果有关的结论;
(3)当t为何值时,以点Q、
A、P为顶点的三角形与ABC相似?解:对于任何时刻t,AP=2t,DQ=t, QA=6-t,当QA=AP时,△QAP为等腰直 角三角形,即6-t=2t,解得t=2(秒)(3)根据题意,可分为两种情况来研究
在矩形ABCD中:①当 = 时,△QAP∽△ABC,则 = ,
解得t= =1.2秒。所以当t=1.2秒时,△QAP∽△ABC。
②当 = 时,△PAQ∽△ABC,则 = ,
解得t=3(秒)。所以当t=3秒时,△PAQ∽△ABC。
(2)在△QAC中,S= QA·DC= ( 6-t)·12=36-6t
在△APC中,S= AP·BC= · 2t·6=6t
QAPC的面积S=(36-6t)+6t=36(cm2)
由计算结果发现:在P、Q两点移动的过程中,
四边形QAPC的面积始终保持不变。解(1)A(-1,0),B(1,0),C(0,-2) 当 △ PDB ∽ △ COB时,
有P(m, 2m-2);(2) 当 △ PDB ∽ △ BOC时, =
有P(m, - )
分类必须有一定的标准,标准不同分类的结果也就不同。分类要做到不遗漏,不重复。分类后,对每个类进行研究,使问题在各种不同的情况下,分别得到各种结论,这就是讨论。分类讨论思想分类讨论是对问题深入研究的思想方法,用分类讨论的思想,有助于发现解题思路和掌握技能技巧,做到举一反三,触类旁通。
分类的思想随处可见,既有概念的分类:如实数、有理数、绝对值、点(直线、圆)与圆的位置关系和两圆相切等概念的分类;又有解题方法上的分类,如代数式中含有字母系数的方程、不等式;还有几何中图形位置关系不确定的分类,等腰三角形的顶角顶点不确定、相似三角形的对应关系不确定等。 zxxk 一.与概念有关的分类1. 一次函数y=kx+b的自变量的取值范围是
-3≤x≤ 6,,相应的函数值的取值范围是
-5≤y≤-2 ,则这个函数的解析式 。解析式为 Y= x-4, 或 y=- x-3 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?OD150°⌒CaEFH探索题1:二.图形位置的分类探索题2: 在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形!1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论(分类讨论)3. 如图,直线AB经过圆O的圆心,与圆O交于A、B两点,点C在O上,且∠AOC=30度,点P是直线AB上的一个动点(与点O不重合),直线PC与圆O相交于点Q,问点P在直线AB的什么位置时,QP=QO?这样的点P有几个?并相应地求出∠OCP的度数。解:∵OQ=OC,OQ=OP ∴∠OQC=∠OCQ,∠QOP=∠QPO 设∠OCP=x度 , 则有:(2)如果点P在线段OB上,显然有PQ>OQ,所以点P不可能在线段OB上。(1)如上图, 当点P在线段OA上时, ∵∠OQC=∠OCP=x,
∴∠QPO=(180-∠OQP)=(180-x)
又∠QPO=∠OCP+∠COP,(180-x)=x+30,
解得x=40, 即∠OCP=40度(3)如图,当点P在的OA延长线上时,
∵∠OQC=∠OCQ=180-x,
∴∠OPQ= (180-x)= x.
又∵∠QCO=∠CPO+∠COP,∴180-x=x+30,
解得x=100 即∠OCP=100度(4)如图当P在OB的延长线上时,
∵∠OQC=∠OCQ=x,∴∠OQC=∠QPO+∠QOP,
∴∠QPO= ∠OQC= x,
又∠COA=∠OCP+∠CPO, 解方程30=x+ x,
得到x=20 即∠OCP=20度6。在Rt△ABC中,∠C=90,AC=3,BC=4。若以C为圆心,R为半径的圆与斜边只有一个公共点,则R的值为多少?4。在半径为1的圆O中,弦AB、AC的长分别是 ,
则∠BAC的度数是 。5。△ABC是半径为2cm的圆的内接三角形,
若BC=2 cm,则角A的度数是 。7..半径为R的两个等圆外切,则半径为2R且和这两个圆都相切的圆有几个?三.与相似三角形有关的分类8。在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动。如果P、Q同时出发,用t秒表示移动的时间(0<x<6)那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QAPC的面积;
提出一个与计算结果有关的结论;
(3)当t为何值时,以点Q、
A、P为顶点的三角形与ABC相似?解:对于任何时刻t,AP=2t,DQ=t, QA=6-t,当QA=AP时,△QAP为等腰直 角三角形,即6-t=2t,解得t=2(秒)(3)根据题意,可分为两种情况来研究
在矩形ABCD中:①当 = 时,△QAP∽△ABC,则 = ,
解得t= =1.2秒。所以当t=1.2秒时,△QAP∽△ABC。
②当 = 时,△PAQ∽△ABC,则 = ,
解得t=3(秒)。所以当t=3秒时,△PAQ∽△ABC。
(2)在△QAC中,S= QA·DC= ( 6-t)·12=36-6t
在△APC中,S= AP·BC= · 2t·6=6t
QAPC的面积S=(36-6t)+6t=36(cm2)
由计算结果发现:在P、Q两点移动的过程中,
四边形QAPC的面积始终保持不变。解(1)A(-1,0),B(1,0),C(0,-2) 当 △ PDB ∽ △ COB时,
有P(m, 2m-2);(2) 当 △ PDB ∽ △ BOC时, =
有P(m, - )
同课章节目录
