平行线分线段成比例的应用
图片预览



文档简介
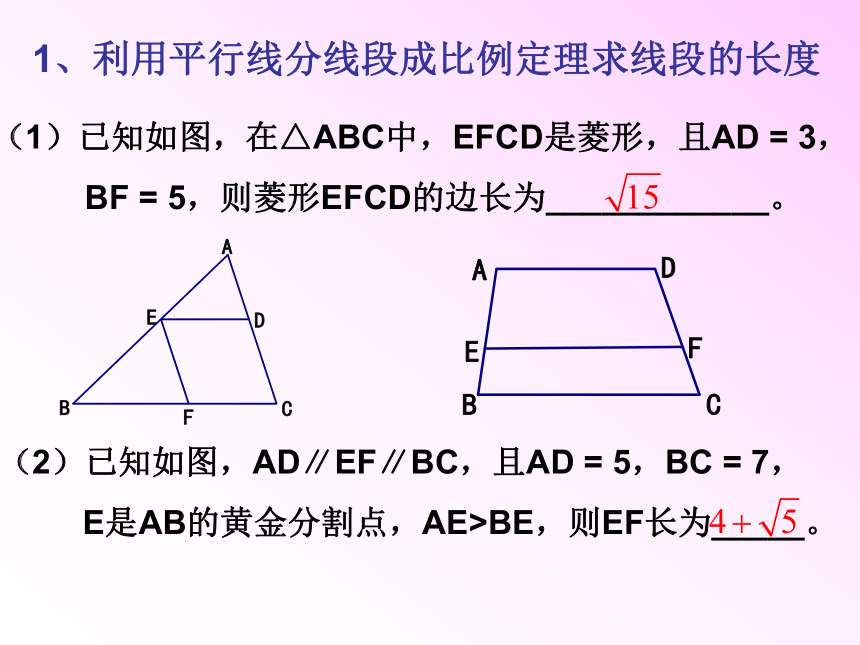
课件11张PPT。平行线分线段成比例1、利用平行线分线段成比例定理求线段的长度(1)已知如图,在△ABC中,EFCD是菱形,且AD = 3,
BF = 5,则菱形EFCD的边长为____________。(2)已知如图,AD∥EF∥BC,且AD = 5,BC = 7,
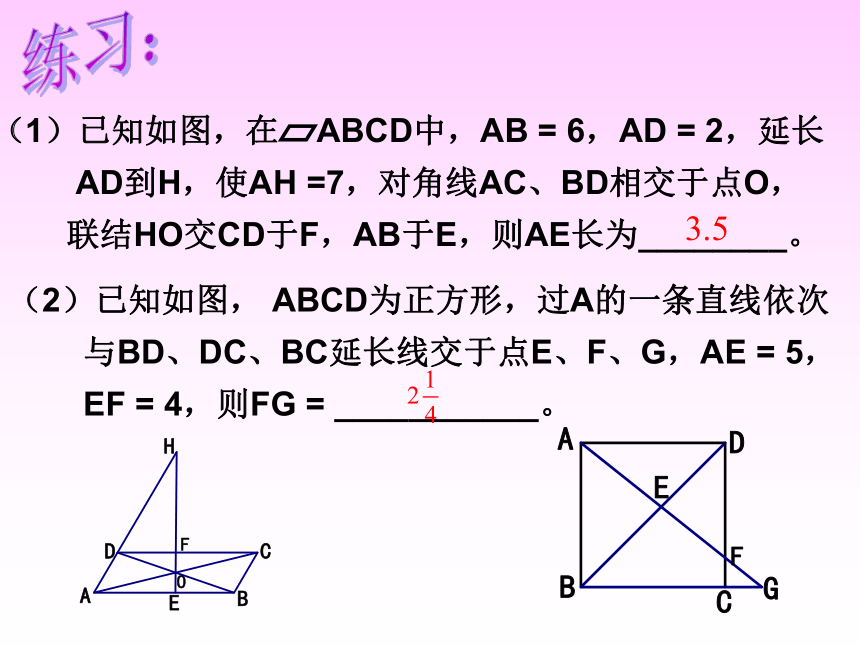
E是AB的黄金分割点,AE>BE,则EF长为_____。(2)已知如图, ABCD为正方形,过A的一条直线依次
与BD、DC、BC延长线交于点E、F、G,AE = 5,
EF = 4,则FG = ___________。练习:2、利用平行线分线段成比例定理求线段的比(2)已知如图,△ABC中,AB=AC,AD⊥BC于点D,
DE :AE = 1 :2,则AF :AB的值为________。53、利用平行线分线段成比例定理作图(1)任意等分线段(a)三等分一条线段(b)将一条线段分成 3 :2两部分(2)作第四比例项已知线段a,b,c,作线段x,使4、运用平行线分线段成比例定理
解决求证比例式或等积式成立。(1)已知如图,D为△ABC中BC上一点,EF∥BC,交
AD 于点H,求证:(3)已知如图,D为△ABC中AC边的中点,过点D的任
意直线交AB于点E,交BC的延长线于点F
求证:BE·CF = BF·EA(4)已知如图,△ABC中,DE∥BC,CD、BE交于点
O,过点O作MN∥BC,分别交AB、AC于点M、N
求证:5、运用平行线分线段成比例定理证明线段相等 (1)如图,已知四边形ABCD是正方形,FG∥CD,
求证:FG = BF(2)如图,D、E是△ABC的AB、BC上的点,联结DE
并延长交AC的延长线于点F,BD :DE = AB :AC,
求证: △EFC是等腰三角形
BF = 5,则菱形EFCD的边长为____________。(2)已知如图,AD∥EF∥BC,且AD = 5,BC = 7,
E是AB的黄金分割点,AE>BE,则EF长为_____。(2)已知如图, ABCD为正方形,过A的一条直线依次
与BD、DC、BC延长线交于点E、F、G,AE = 5,
EF = 4,则FG = ___________。练习:2、利用平行线分线段成比例定理求线段的比(2)已知如图,△ABC中,AB=AC,AD⊥BC于点D,
DE :AE = 1 :2,则AF :AB的值为________。53、利用平行线分线段成比例定理作图(1)任意等分线段(a)三等分一条线段(b)将一条线段分成 3 :2两部分(2)作第四比例项已知线段a,b,c,作线段x,使4、运用平行线分线段成比例定理
解决求证比例式或等积式成立。(1)已知如图,D为△ABC中BC上一点,EF∥BC,交
AD 于点H,求证:(3)已知如图,D为△ABC中AC边的中点,过点D的任
意直线交AB于点E,交BC的延长线于点F
求证:BE·CF = BF·EA(4)已知如图,△ABC中,DE∥BC,CD、BE交于点
O,过点O作MN∥BC,分别交AB、AC于点M、N
求证:5、运用平行线分线段成比例定理证明线段相等 (1)如图,已知四边形ABCD是正方形,FG∥CD,
求证:FG = BF(2)如图,D、E是△ABC的AB、BC上的点,联结DE
并延长交AC的延长线于点F,BD :DE = AB :AC,
求证: △EFC是等腰三角形
