人教版数学七年级上册 1.2.5 有理数大小的比较 课件(共17张PPT)
文档属性
| 名称 | 人教版数学七年级上册 1.2.5 有理数大小的比较 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 277.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 22:05:31 | ||
图片预览






文档简介
(共17张PPT)
1.2.5 有理数大小的比较
教学目标
(1)知道比较有理数大小的法则.
(2)会比较两个有理数的大小.
教学重难点
有理数比较大小的法则.
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
讲授新课
借助数轴比较有理数的大小
一
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
试一试:我们把这些数在数轴上表示的话,
我们看看他们在数轴上呈现什么规律?
越 来 越 大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20 -10 0 5 10
●
●
●
●
●
我们可以看出:
①数轴上的数由左到右是从小到大排列;
②数轴上的数左边的数小于右边的数.
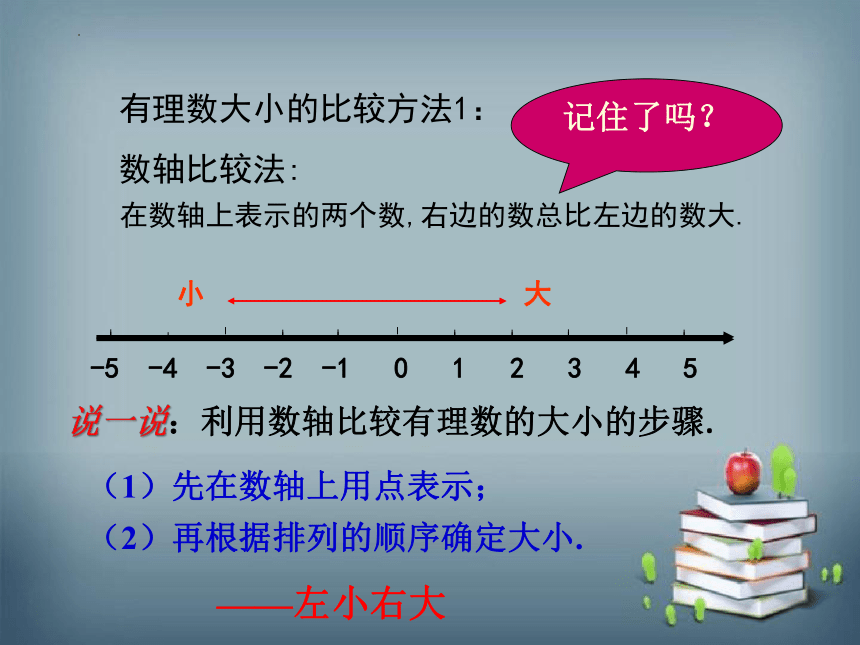
记住了吗?
有理数大小的比较方法1:
数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
说一说:利用数轴比较有理数的大小的步骤.
(1)先在数轴上用点表示;
(2)再根据排列的顺序确定大小.
——左小右大
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
-5 -3 0 4
例1 在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5 <-3 <0 <4
典例精析
如图,数轴上A,B,C三点表示的数分别为a,b,c,则它们的大小关系是( )
A.a>b>c B.b>c>a C.c>a>b D.b>a>c
针对训练
D
运用法则比较有理数的大小
二
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
一定要借助数轴吗?能不能直接比较?
思考:
分析:
小学学习到正数与正数的大小比较.
利用数轴,可看出正数>0;
负数<0;
正数>负数.
负数与负数的大小比较.
还差什么?
运用法则比较有理数的大小
二
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
负数:-1、-2、-3、-4、-5.
.
.
.
.
越向左去的点,表示的数越
.
小.
越大
绝对值大的反而小.
两个负数比较大小:
但它们 离原点的距离 呢?
绝对值
运用法则比较有理数的大小
二
两个负数比较大小的步骤:
(1)先分别求两数的绝对值;
(2)再比较绝对值,绝对值越大,原来的负数就越小.
学习了负数与负数的大小比较后,我们可以比较任意两个有理数的大小.
①正数>0 ②负数<0
③正数>负数
④两个负数,绝对值大的反而小.
例2:比较下列各组数的大小:
(3)-0.2与-0.25;
(6) 与 .
(5) 与 ;
(4)-0.1与-0.01;
(1)-2与-3; (2) 与-0.8;
解:(1)-2>-3;
(2) >-0.8;
(3)-0.2>-0.25;
(4)-0.1<-0.01;
(5) > ;
(6) > .
从上面的比较,我们可以看出:
①不同符号的数比较大小,只看符号;
②相同符号的数比较大小,看符号的同时,还要判断绝对值的大小.
同是正数的时候绝对值越大就越大,
同是负数的时候绝对值越大反而小.
例3. 比较下列各数的大小.
解:先化简,-(-3)=3,
-(+2)=-2,
因为正数大于负数,所以3>-2,即
-(-3)>-(+2)
(1)-(-3)和-(+2);
异号两数比较要考虑它们的正负.
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
解:先化简:
课堂小结
比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左 边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
课堂小结
1.2.5 有理数大小的比较
教学目标
(1)知道比较有理数大小的法则.
(2)会比较两个有理数的大小.
教学重难点
有理数比较大小的法则.
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
讲授新课
借助数轴比较有理数的大小
一
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
试一试:我们把这些数在数轴上表示的话,
我们看看他们在数轴上呈现什么规律?
越 来 越 大
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
-20 -10 0 5 10
●
●
●
●
●
我们可以看出:
①数轴上的数由左到右是从小到大排列;
②数轴上的数左边的数小于右边的数.
记住了吗?
有理数大小的比较方法1:
数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
说一说:利用数轴比较有理数的大小的步骤.
(1)先在数轴上用点表示;
(2)再根据排列的顺序确定大小.
——左小右大
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
-5 -3 0 4
例1 在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5 <-3 <0 <4
典例精析
如图,数轴上A,B,C三点表示的数分别为a,b,c,则它们的大小关系是( )
A.a>b>c B.b>c>a C.c>a>b D.b>a>c
针对训练
D
运用法则比较有理数的大小
二
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
一定要借助数轴吗?能不能直接比较?
思考:
分析:
小学学习到正数与正数的大小比较.
利用数轴,可看出正数>0;
负数<0;
正数>负数.
负数与负数的大小比较.
还差什么?
运用法则比较有理数的大小
二
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
负数:-1、-2、-3、-4、-5.
.
.
.
.
越向左去的点,表示的数越
.
小.
越大
绝对值大的反而小.
两个负数比较大小:
但它们 离原点的距离 呢?
绝对值
运用法则比较有理数的大小
二
两个负数比较大小的步骤:
(1)先分别求两数的绝对值;
(2)再比较绝对值,绝对值越大,原来的负数就越小.
学习了负数与负数的大小比较后,我们可以比较任意两个有理数的大小.
①正数>0 ②负数<0
③正数>负数
④两个负数,绝对值大的反而小.
例2:比较下列各组数的大小:
(3)-0.2与-0.25;
(6) 与 .
(5) 与 ;
(4)-0.1与-0.01;
(1)-2与-3; (2) 与-0.8;
解:(1)-2>-3;
(2) >-0.8;
(3)-0.2>-0.25;
(4)-0.1<-0.01;
(5) > ;
(6) > .
从上面的比较,我们可以看出:
①不同符号的数比较大小,只看符号;
②相同符号的数比较大小,看符号的同时,还要判断绝对值的大小.
同是正数的时候绝对值越大就越大,
同是负数的时候绝对值越大反而小.
例3. 比较下列各数的大小.
解:先化简,-(-3)=3,
-(+2)=-2,
因为正数大于负数,所以3>-2,即
-(-3)>-(+2)
(1)-(-3)和-(+2);
异号两数比较要考虑它们的正负.
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
解:先化简:
课堂小结
比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左 边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
课堂小结
