人教版数学七年级上册 1.2.5 有理数大小比较 课件(共25张PPT)
文档属性
| 名称 | 人教版数学七年级上册 1.2.5 有理数大小比较 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 22:08:53 | ||
图片预览






文档简介
(共25张PPT)
1.2.5 有理数大小比较
1、比较有理数的大小。
2、利用绝对值比较两个负数的有理数大小。
重点
比较有理数的大小。
难点
利用绝对值比较两个负数的有理数大小。
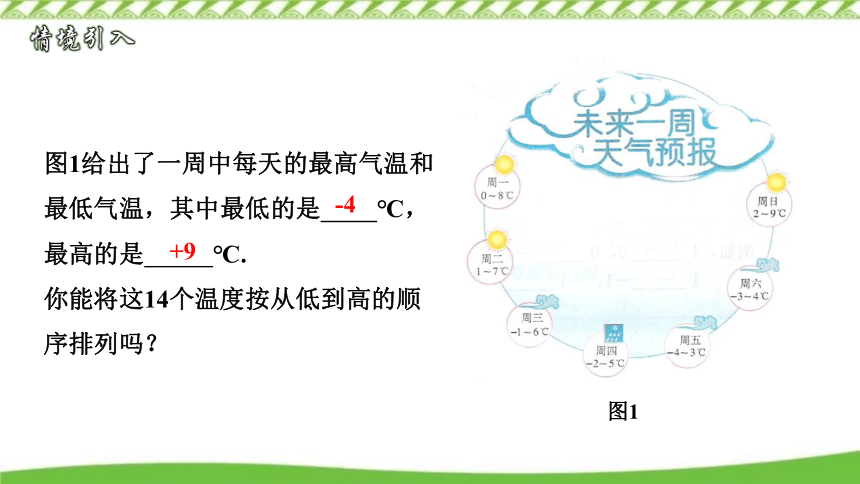
图1给出了一周中每天的最高气温和最低气温,其中最低的是 ℃,最高的是 ℃.
你能将这14个温度按从低到高的顺序排列吗?
图1
-4
+9
-5
-3
-4
-1
-2
0
2
1
4
3
5
7
6
9
8
10
从上面图1.2-6中,我们可以看出温度从低到高排列为:
-4,-3,-2,-1,0,1,2,3,4,5,6 …
我们把这些数在数轴上表示的话,我们看看他们在数轴上呈现什么规律?
我们可以看出:
①数轴上的数由左到右是从小到大排列;
②数轴上的数左边的数小于右边的数.
数轴上不同的两个点表示的数,右边点表示的数总比左边的点表示的数大.
-3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11
-2.5 < -0.8 < 0 < 6 < 10
小
大
说一说:利用数轴比较有理数的大小的步骤.
(1)先在数轴上用点表示;
(2)再根据排列的顺序确定大小.
——左小右大
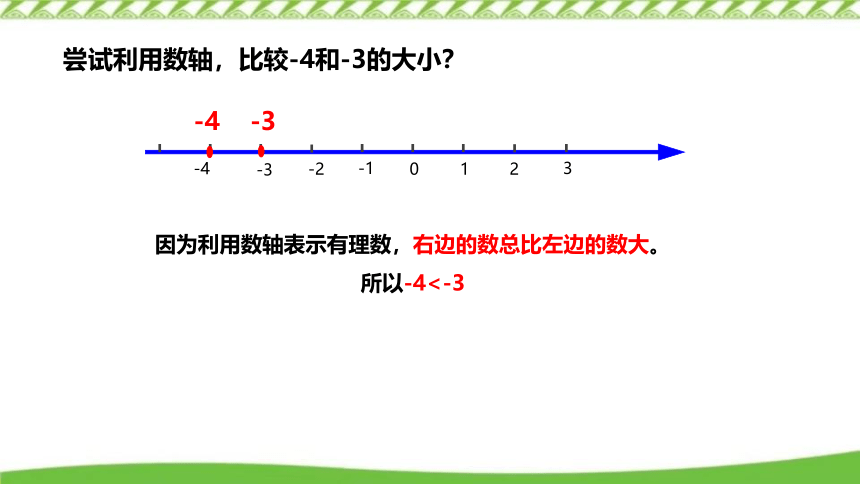
尝试利用数轴,比较-4和-3的大小?
0
2
1
3
-1
-2
-3
-4
因为利用数轴表示有理数,右边的数总比左边的数大。所以-4<-3
-4 -3
-10 -8 -6 -4 -2 0 2 4 6 8 10 12
把下列各数表示在数轴上,并用“<”把它们连接起来:
-8, 3,-10,-4, 2, 12.
.
.
.
.
.
.
-10 -8 -4 2 3 12
-10<-8 <-4 < 2 < 3 < 12
有理数的大小比较,一定要借助于数轴吗?
能直接进行比较吗?
思考:
分析:
小学学习到正数与正数的大小比较.
利用数轴,可看出正数>0;
负数<0;
正数>负数.
负数与负数的大小比较.
还差什么?
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
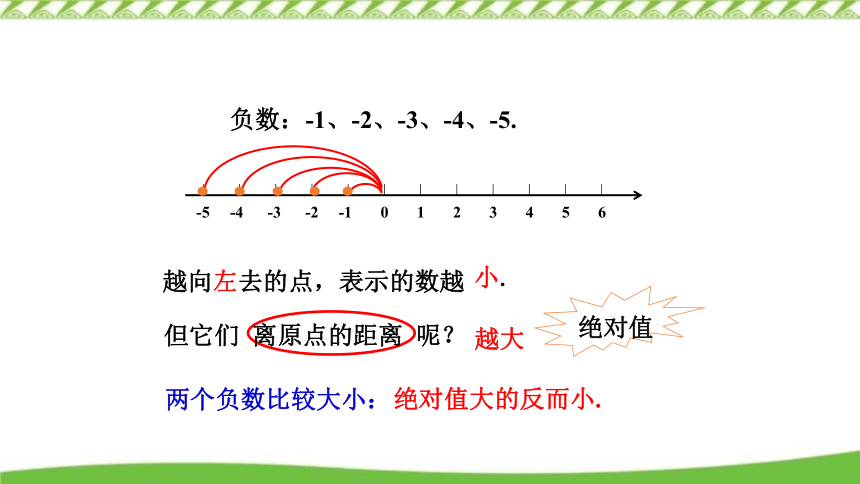
负数:-1、-2、-3、-4、-5.
.
.
.
.
越向左去的点,表示的数越
.
小.
越大
绝对值大的反而小.
两个负数比较大小:
但它们 离原点的距离 呢?
绝对值
两个负数比较大小的步骤:
(1)先分别求两数的绝对值;
(2)再比较绝对值,绝对值越大,原来的负数就越小.
学习了负数与负数的大小比较后,我们可以比较任意两个有理数的大小.
利用数轴比较有理数的大小的步骤:
1)画数轴;
2)把要比较的数在数轴上表示出来;
3)用“<”号从左至右将各数连接起来或用“>”号从右至左将各数连接起来。
如果不借助数轴,如何比较两个负数的的大小?(例: -4和-3 )
因为|-4|=4,|-3|=3,
可以理解为表示-4的点在原点左侧,距原点4个单位长度
表示-3的点在原点左侧,距原点3个单位长度
所以,表示-3的点距原点较近,且在表示-4的点的右侧
则-4<-3。
即两个负数比较大小时,绝对值大的反而小。
有理数比较大小方法总结
例1:比较下列各组数的大小:
(3)-0.2与-0.25;
(6) 与 .
(5) 与 ;
(4)-0.1与-0.01;
(1)-2与-3; (2) 与-0.8;
解:(1)-2>-3;
(2) >-0.8;
(3)-0.2>-0.25;
(4)-0.1<-0.01;
(5) > ;
(6) > .
从上面的比较,我们可以看出:
①不同符号的数比较大小,只看符号;
②相同符号的数比较大小,看符号的同时,还要判断绝对值的大小.
同是正数的时候绝对值越大就越大,
同是负数的时候绝对值越大反而小.
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
例2 在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5<-3<0<4
例3 比较下列各数的大小.
(1)-(-3)和-(+2);
解:(1)先化简,-(-3)=3,-(+2)=-2,
∵正数大于负数,∴3>-2,
即:-(-3)>-(+2)
异号两数比较要考虑它们的正负.
(2)两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
例4 如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
A.点M B.点N C.点P D.点Q
【答案】C
【解析】
∵点M,N表示的有理数互为相反数,
∴原点的位置大约在O点,
∴绝对值最小的数的点是P点,故选C.
1.(2022 郴州)有理数-2, ,0, 中,绝对值最大的数是( )
A.-2 B. C.0 D.
【解答】解:-2的绝对值是2, 的绝对值是 ,0的绝对值是0, 的绝对值是 .
因为 ,
所以-2的绝对值最大.
故选A.
2.若a,b是有理数,那么下列结论一定正确的是( )
A.若ab,则│a│>│b│
C.若a=b,则│a│=│b│ D.若a≠b,则│a│≠│b│
【答案】C
【解析】
A、若a=﹣1,b=0,则|﹣1|>|0|,所以A选项错误;
B、若a=0,b=﹣1,则|0|<|﹣1|,所以B选项错误;
C、若a=b,则|a|=|b|,所以C选项正确;
D、若a=﹣1,b=1,则|﹣1|=|1|,所以D选项错误.故选C.
3. 比较,,的大小,结果正确的是( )
A.<< B.<< C.<< D.<<
【答案】A
【解析】
解:∵<0,<0,>0∴最大;
又∵ > ,∴<;
∴<<.故选A.
4.如果a是有理数,试比较|a|与-2a的大小.
解: 当a>0时,|a|>0,-2a<0,所以|a|>-2a;
当a=0时,|a|=0,-2a=0,所以|a|=-2a;
当a<0时,-2a>0,|a|=-a,
因为-2a>-a,所以|a|<-2a.
5.下列判断,正确的是( )
A.若a>b,则│a│>│b│
B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│
D.若a>b>0,则│a│>│b│
D
×
如a=1,b=-2
×
如a=-3,b=2
×
如a=-3,b=-2
√
比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左 边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
谢谢聆听
1.2.5 有理数大小比较
1、比较有理数的大小。
2、利用绝对值比较两个负数的有理数大小。
重点
比较有理数的大小。
难点
利用绝对值比较两个负数的有理数大小。
图1给出了一周中每天的最高气温和最低气温,其中最低的是 ℃,最高的是 ℃.
你能将这14个温度按从低到高的顺序排列吗?
图1
-4
+9
-5
-3
-4
-1
-2
0
2
1
4
3
5
7
6
9
8
10
从上面图1.2-6中,我们可以看出温度从低到高排列为:
-4,-3,-2,-1,0,1,2,3,4,5,6 …
我们把这些数在数轴上表示的话,我们看看他们在数轴上呈现什么规律?
我们可以看出:
①数轴上的数由左到右是从小到大排列;
②数轴上的数左边的数小于右边的数.
数轴上不同的两个点表示的数,右边点表示的数总比左边的点表示的数大.
-3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11
-2.5 < -0.8 < 0 < 6 < 10
小
大
说一说:利用数轴比较有理数的大小的步骤.
(1)先在数轴上用点表示;
(2)再根据排列的顺序确定大小.
——左小右大
尝试利用数轴,比较-4和-3的大小?
0
2
1
3
-1
-2
-3
-4
因为利用数轴表示有理数,右边的数总比左边的数大。所以-4<-3
-4 -3
-10 -8 -6 -4 -2 0 2 4 6 8 10 12
把下列各数表示在数轴上,并用“<”把它们连接起来:
-8, 3,-10,-4, 2, 12.
.
.
.
.
.
.
-10 -8 -4 2 3 12
-10<-8 <-4 < 2 < 3 < 12
有理数的大小比较,一定要借助于数轴吗?
能直接进行比较吗?
思考:
分析:
小学学习到正数与正数的大小比较.
利用数轴,可看出正数>0;
负数<0;
正数>负数.
负数与负数的大小比较.
还差什么?
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
负数:-1、-2、-3、-4、-5.
.
.
.
.
越向左去的点,表示的数越
.
小.
越大
绝对值大的反而小.
两个负数比较大小:
但它们 离原点的距离 呢?
绝对值
两个负数比较大小的步骤:
(1)先分别求两数的绝对值;
(2)再比较绝对值,绝对值越大,原来的负数就越小.
学习了负数与负数的大小比较后,我们可以比较任意两个有理数的大小.
利用数轴比较有理数的大小的步骤:
1)画数轴;
2)把要比较的数在数轴上表示出来;
3)用“<”号从左至右将各数连接起来或用“>”号从右至左将各数连接起来。
如果不借助数轴,如何比较两个负数的的大小?(例: -4和-3 )
因为|-4|=4,|-3|=3,
可以理解为表示-4的点在原点左侧,距原点4个单位长度
表示-3的点在原点左侧,距原点3个单位长度
所以,表示-3的点距原点较近,且在表示-4的点的右侧
则-4<-3。
即两个负数比较大小时,绝对值大的反而小。
有理数比较大小方法总结
例1:比较下列各组数的大小:
(3)-0.2与-0.25;
(6) 与 .
(5) 与 ;
(4)-0.1与-0.01;
(1)-2与-3; (2) 与-0.8;
解:(1)-2>-3;
(2) >-0.8;
(3)-0.2>-0.25;
(4)-0.1<-0.01;
(5) > ;
(6) > .
从上面的比较,我们可以看出:
①不同符号的数比较大小,只看符号;
②相同符号的数比较大小,看符号的同时,还要判断绝对值的大小.
同是正数的时候绝对值越大就越大,
同是负数的时候绝对值越大反而小.
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
例2 在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5<-3<0<4
例3 比较下列各数的大小.
(1)-(-3)和-(+2);
解:(1)先化简,-(-3)=3,-(+2)=-2,
∵正数大于负数,∴3>-2,
即:-(-3)>-(+2)
异号两数比较要考虑它们的正负.
(2)两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
例4 如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
A.点M B.点N C.点P D.点Q
【答案】C
【解析】
∵点M,N表示的有理数互为相反数,
∴原点的位置大约在O点,
∴绝对值最小的数的点是P点,故选C.
1.(2022 郴州)有理数-2, ,0, 中,绝对值最大的数是( )
A.-2 B. C.0 D.
【解答】解:-2的绝对值是2, 的绝对值是 ,0的绝对值是0, 的绝对值是 .
因为 ,
所以-2的绝对值最大.
故选A.
2.若a,b是有理数,那么下列结论一定正确的是( )
A.若a
C.若a=b,则│a│=│b│ D.若a≠b,则│a│≠│b│
【答案】C
【解析】
A、若a=﹣1,b=0,则|﹣1|>|0|,所以A选项错误;
B、若a=0,b=﹣1,则|0|<|﹣1|,所以B选项错误;
C、若a=b,则|a|=|b|,所以C选项正确;
D、若a=﹣1,b=1,则|﹣1|=|1|,所以D选项错误.故选C.
3. 比较,,的大小,结果正确的是( )
A.<< B.<< C.<< D.<<
【答案】A
【解析】
解:∵<0,<0,>0∴最大;
又∵ > ,∴<;
∴<<.故选A.
4.如果a是有理数,试比较|a|与-2a的大小.
解: 当a>0时,|a|>0,-2a<0,所以|a|>-2a;
当a=0时,|a|=0,-2a=0,所以|a|=-2a;
当a<0时,-2a>0,|a|=-a,
因为-2a>-a,所以|a|<-2a.
5.下列判断,正确的是( )
A.若a>b,则│a│>│b│
B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│
D.若a>b>0,则│a│>│b│
D
×
如a=1,b=-2
×
如a=-3,b=2
×
如a=-3,b=-2
√
比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左 边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
谢谢聆听
