数学人教版七年级上册 2.1.2 多项式与整式 课件(共25张PPT)
文档属性
| 名称 | 数学人教版七年级上册 2.1.2 多项式与整式 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 285.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 07:34:36 | ||
图片预览




文档简介
(共25张PPT)
2.1.2 多项式与整式
教学目标
1.能叙述并理解多项式、多项式的项、常数项及其次数的概念.
2.知道什么叫整式,弄清整式与多项式、单项式的关系.
3.通过小组讨论、合作交流,使学生经历新知的形成过程,培养比较、分析、归纳的能力.
4.初步体会类比和逆向思维的数学思想.
教学重难点
教学重点
掌握多项式的定义、多项式的项和次数,以及常数项等概念.弄清整式与多项式、单项式的关系
教学难点
多项式的次数.
计算:
1. -2a2·4a3 b 2. (x-3y)(-6x) 3. x(x-y)-y(x+y)
复习回顾
解:1. -2a2·4a3 b =-8a5 b
2. (x-3y)(-6x)=-6x2 +18xy
3. x(x-y)-y(x+y)
=x2 - xy-xy-y2
=x2 - 2xy-y2
单项式乘单项式法则
单项式乘多项式法则
单项式乘多项式法则
合并同类项法则
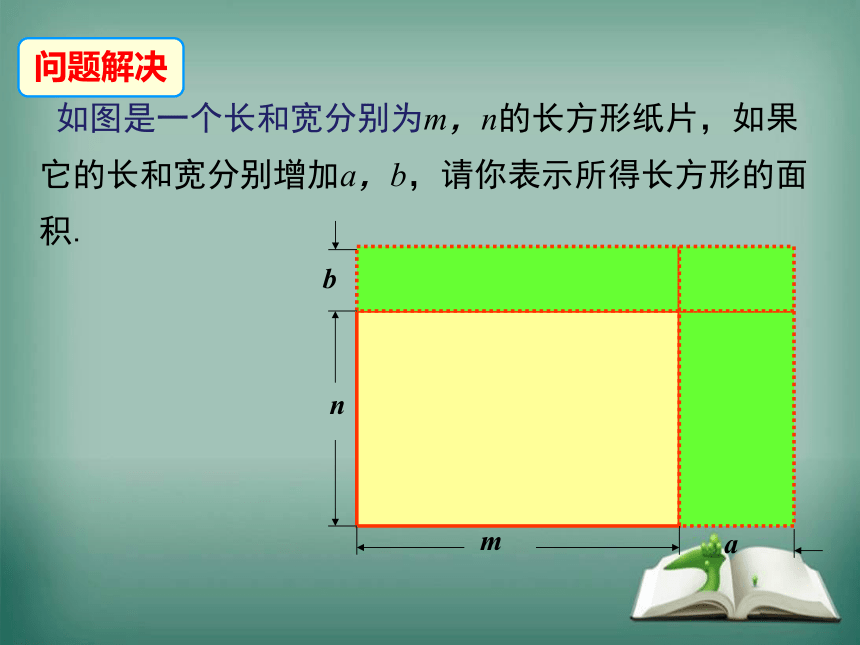
如图是一个长和宽分别为m,n的长方形纸片,如果它的长和宽分别增加a,b,请你表示所得长方形的面积.
n
m
b
a
问题解决
n
m
b
a
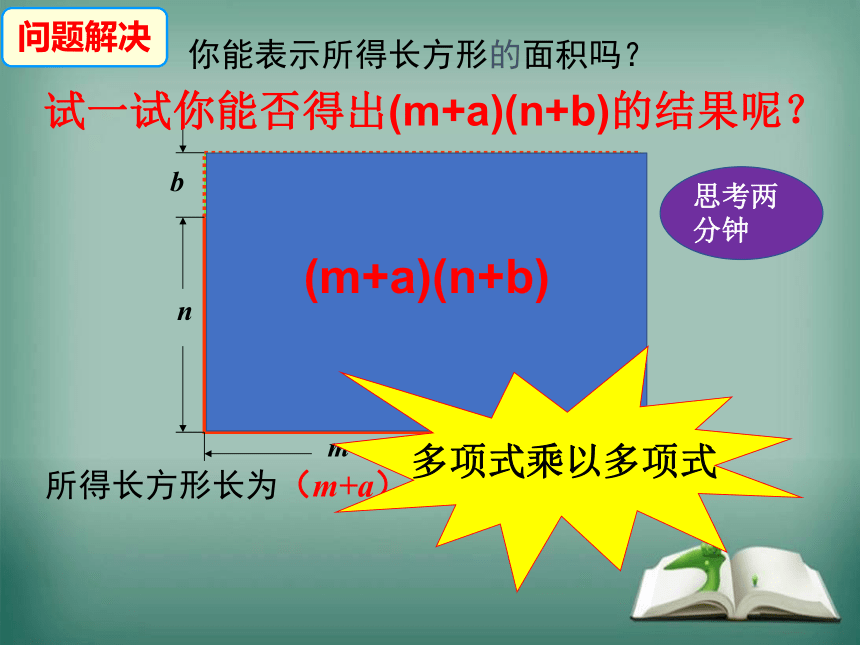
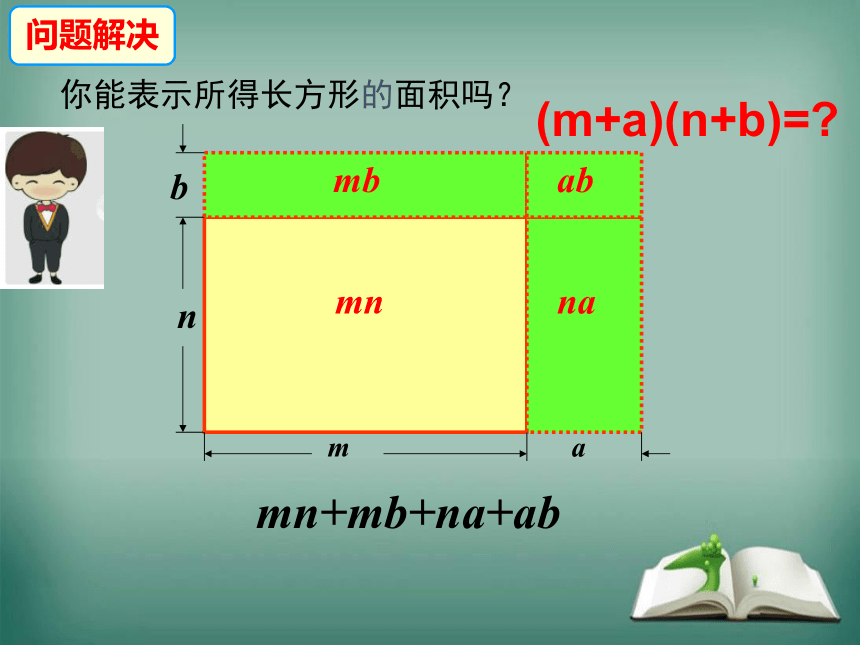
你能表示所得长方形的面积吗?
(m+a)(n+b)
问题解决
所得长方形长为(m+a)米,宽为(n+b)米
多项式乘以多项式
试一试你能否得出(m+a)(n+b)的结果呢?
思考两分钟
n
m
b
a
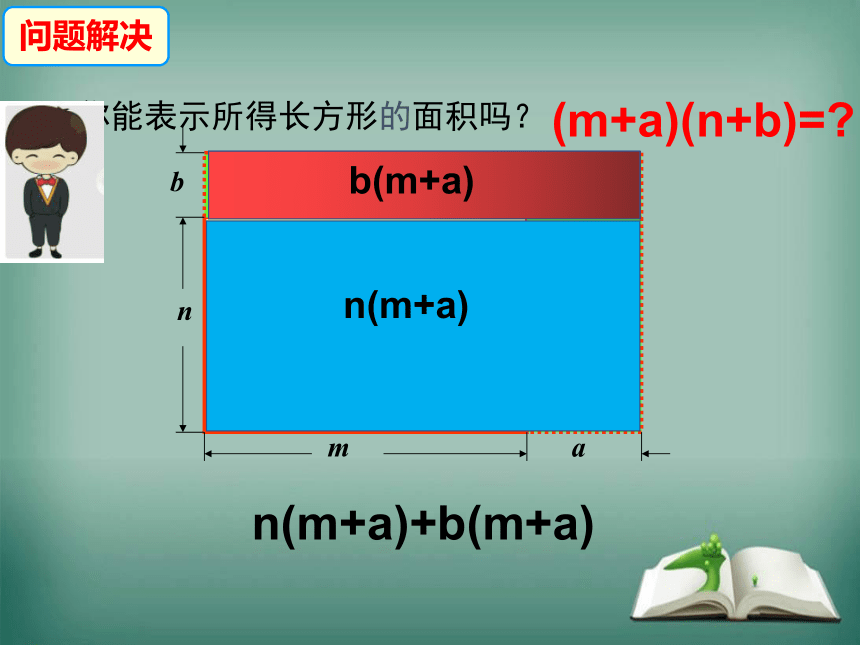
你能表示所得长方形的面积吗?
b(m+a)
n(m+a)
n(m+a)+b(m+a)
问题解决
(m+a)(n+b)=
n
m
b
a
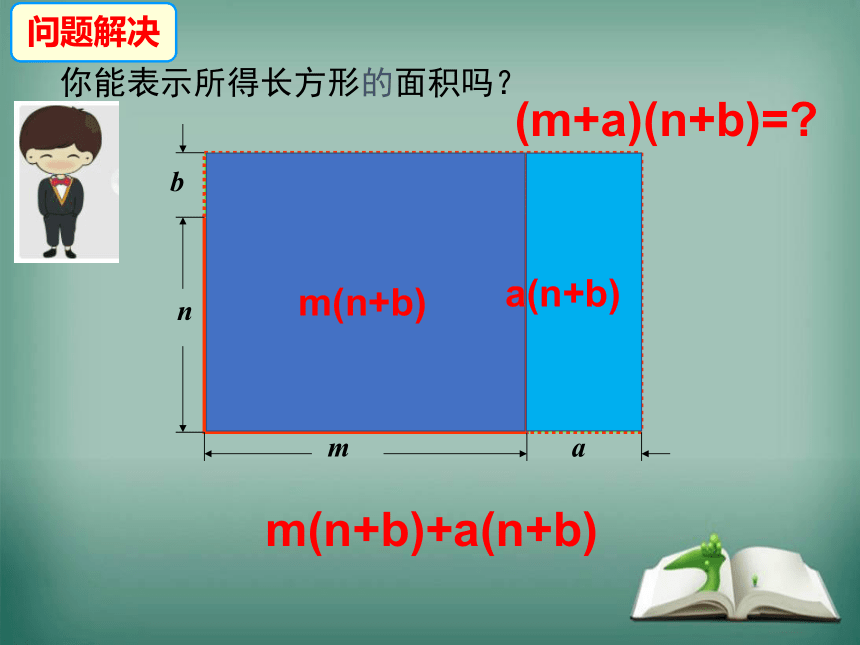
你能表示所得长方形的面积吗?
m(n+b)
a(n+b)
m(n+b)+a(n+b)
问题解决
(m+a)(n+b)=
mn
na
mb
ab
n
m
b
a
你能表示所得长方形的面积吗?
mn+mb+na+ab
问题解决
(m+a)(n+b)=
(m+a)(n+b)
n(m+a)+b(m+a)
m(n+b)+a(n+b)
mn+mb+na+ab
=
=
=
互助探究
小明通过面积算出了结果,观察,你能不能说明其中的道理呢?
(m+a)(n+b)=
mn+mb+na+ab
思考两分钟
(m+a)
n +b
mn+mb+na+ab
=
=
(n+b)
(m+a)
(m+n)
互助探究
多项式×多项式
单项式×多项式
转化
整体
(m+a)(n+b)
n(m+a)+b(m+a)
m(n+b)+a(n+b)
mn+mb+na+ab
=
=
=
互助探究
转化
mn
na
mb
ab
n
m
b
a
(m+a)(n+b)=mn+mb+na+ab
由上面的探索,我们得到:
思考:如何进行多项式与多项式相乘
的运算呢?
思考一分钟
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
知识要点
多项式乘以多项式
1
2
3
4
(m+a)(n+b)
=
mn
1
2
3
4
mb
an
ab
总结归纳
+
+
+
典例精析
例1 计算:(1)(1-x)(0.6-x); (2)(2x+y)(x-y)
(1) 原式=
1×0.6
1×(-x)
(-x)·0.6
(-x)·(-x)
+
+
+
= 0.6-x-0.6x+x2
单项式乘多项式法则
合并同类项法则
= 0.6-1.6x+x2
多项式乘多项式法则
(2) 原式=2x·x+2x·(-y)+y·x+y·(-y)
=2x2-2xy+xy-y2
=2x2-xy-y2;
多项式乘多项式法则
合并同类项法则
单项式乘多项式法则
解:
例2:(1) (x+y)(x2-xy+y2). (2) ( x+2y)2
多项式乘多项式法则
合并同类项法则
.
注意:(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式(是同类项的要合并).
单项式乘单项式法则
= x3+y3
例3 先化简,再求值:(3x-1)(2x-3)-(6x-5)(x-4),
其中x=-2.
当a=-2时,原式=-36-17=-53.
方法总结:化简求值的题型,一定要注意先化简,
再求值,不能先代值,再计算.
当堂练习
错
错
( 1)不要漏乘、漏项;(2)符号问题 .
注意:
1.下列计算对吗?若不对,应该怎样改?
2.计算:(1)(x 3y)(x+7y); (2)(2x + 5y)(3x 2y-1).
解:
(1) (x 3y)(x+7y)
+
7xy
3yx
=
x2 +4xy-21y2
21y2
(2) (2x +5 y)(3x 2y-1)
=
=x2
2x 3x
2x 2y
-2x 1+5 y 3x
5y 2y-5y 1
=
6x2
4xy-2x
+ 15xy
10y2
=
6x2 +11xy-2x 10y2-5y
-5y
每一步思考:计算过程中每一步运算的依据是什么?
思考:计算过程中每一步
运算的依据是什么?
3. 先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
当a=-1,b=1时,原式=-8+2-15=-21.
每一步思考:计算过程中每一步运算的依据是什么?
思考:计算过程中每一步
运算的依据是什么?
解:(x-2)(x2+mx+1)
=x3+mx2+x-2x2-2mx-2
=x3+mx2-2x2+x-2mx-2
=x3+(m-2)x2+x-2mx-2
∵不含x2项
∴m-2=0
∴m=2
方程
本节课学习了哪些知识?
领悟到哪些解决问题的方法?
感触最深的是什么?
对于本节课的学习还有什么困惑?
收获感悟
实际问题
多项式×多项式运算
多项式×多项式法则
乘法分配律(整体代入
单项式×多项式
课堂总结
运用法则解决问题
整体思想
转化思想
方程思想
感谢聆听
2.1.2 多项式与整式
教学目标
1.能叙述并理解多项式、多项式的项、常数项及其次数的概念.
2.知道什么叫整式,弄清整式与多项式、单项式的关系.
3.通过小组讨论、合作交流,使学生经历新知的形成过程,培养比较、分析、归纳的能力.
4.初步体会类比和逆向思维的数学思想.
教学重难点
教学重点
掌握多项式的定义、多项式的项和次数,以及常数项等概念.弄清整式与多项式、单项式的关系
教学难点
多项式的次数.
计算:
1. -2a2·4a3 b 2. (x-3y)(-6x) 3. x(x-y)-y(x+y)
复习回顾
解:1. -2a2·4a3 b =-8a5 b
2. (x-3y)(-6x)=-6x2 +18xy
3. x(x-y)-y(x+y)
=x2 - xy-xy-y2
=x2 - 2xy-y2
单项式乘单项式法则
单项式乘多项式法则
单项式乘多项式法则
合并同类项法则
如图是一个长和宽分别为m,n的长方形纸片,如果它的长和宽分别增加a,b,请你表示所得长方形的面积.
n
m
b
a
问题解决
n
m
b
a
你能表示所得长方形的面积吗?
(m+a)(n+b)
问题解决
所得长方形长为(m+a)米,宽为(n+b)米
多项式乘以多项式
试一试你能否得出(m+a)(n+b)的结果呢?
思考两分钟
n
m
b
a
你能表示所得长方形的面积吗?
b(m+a)
n(m+a)
n(m+a)+b(m+a)
问题解决
(m+a)(n+b)=
n
m
b
a
你能表示所得长方形的面积吗?
m(n+b)
a(n+b)
m(n+b)+a(n+b)
问题解决
(m+a)(n+b)=
mn
na
mb
ab
n
m
b
a
你能表示所得长方形的面积吗?
mn+mb+na+ab
问题解决
(m+a)(n+b)=
(m+a)(n+b)
n(m+a)+b(m+a)
m(n+b)+a(n+b)
mn+mb+na+ab
=
=
=
互助探究
小明通过面积算出了结果,观察,你能不能说明其中的道理呢?
(m+a)(n+b)=
mn+mb+na+ab
思考两分钟
(m+a)
n +b
mn+mb+na+ab
=
=
(n+b)
(m+a)
(m+n)
互助探究
多项式×多项式
单项式×多项式
转化
整体
(m+a)(n+b)
n(m+a)+b(m+a)
m(n+b)+a(n+b)
mn+mb+na+ab
=
=
=
互助探究
转化
mn
na
mb
ab
n
m
b
a
(m+a)(n+b)=mn+mb+na+ab
由上面的探索,我们得到:
思考:如何进行多项式与多项式相乘
的运算呢?
思考一分钟
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
知识要点
多项式乘以多项式
1
2
3
4
(m+a)(n+b)
=
mn
1
2
3
4
mb
an
ab
总结归纳
+
+
+
典例精析
例1 计算:(1)(1-x)(0.6-x); (2)(2x+y)(x-y)
(1) 原式=
1×0.6
1×(-x)
(-x)·0.6
(-x)·(-x)
+
+
+
= 0.6-x-0.6x+x2
单项式乘多项式法则
合并同类项法则
= 0.6-1.6x+x2
多项式乘多项式法则
(2) 原式=2x·x+2x·(-y)+y·x+y·(-y)
=2x2-2xy+xy-y2
=2x2-xy-y2;
多项式乘多项式法则
合并同类项法则
单项式乘多项式法则
解:
例2:(1) (x+y)(x2-xy+y2). (2) ( x+2y)2
多项式乘多项式法则
合并同类项法则
.
注意:(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式(是同类项的要合并).
单项式乘单项式法则
= x3+y3
例3 先化简,再求值:(3x-1)(2x-3)-(6x-5)(x-4),
其中x=-2.
当a=-2时,原式=-36-17=-53.
方法总结:化简求值的题型,一定要注意先化简,
再求值,不能先代值,再计算.
当堂练习
错
错
( 1)不要漏乘、漏项;(2)符号问题 .
注意:
1.下列计算对吗?若不对,应该怎样改?
2.计算:(1)(x 3y)(x+7y); (2)(2x + 5y)(3x 2y-1).
解:
(1) (x 3y)(x+7y)
+
7xy
3yx
=
x2 +4xy-21y2
21y2
(2) (2x +5 y)(3x 2y-1)
=
=x2
2x 3x
2x 2y
-2x 1+5 y 3x
5y 2y-5y 1
=
6x2
4xy-2x
+ 15xy
10y2
=
6x2 +11xy-2x 10y2-5y
-5y
每一步思考:计算过程中每一步运算的依据是什么?
思考:计算过程中每一步
运算的依据是什么?
3. 先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
当a=-1,b=1时,原式=-8+2-15=-21.
每一步思考:计算过程中每一步运算的依据是什么?
思考:计算过程中每一步
运算的依据是什么?
解:(x-2)(x2+mx+1)
=x3+mx2+x-2x2-2mx-2
=x3+mx2-2x2+x-2mx-2
=x3+(m-2)x2+x-2mx-2
∵不含x2项
∴m-2=0
∴m=2
方程
本节课学习了哪些知识?
领悟到哪些解决问题的方法?
感触最深的是什么?
对于本节课的学习还有什么困惑?
收获感悟
实际问题
多项式×多项式运算
多项式×多项式法则
乘法分配律(整体代入
单项式×多项式
课堂总结
运用法则解决问题
整体思想
转化思想
方程思想
感谢聆听
