必修1第二章基本初等函数学单元卷(二)A
文档属性
| 名称 | 必修1第二章基本初等函数学单元卷(二)A |  | |
| 格式 | zip | ||
| 文件大小 | 121.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-09 10:27:00 | ||
图片预览



文档简介
2007—2008学年第一学期高一数学单元卷(二)A
(内容:必修1第二章基本初等函数)
(满分:150分;考试时间:100分钟)
一、选择题(本大题共12小题. 每小题5分,共60分。 在每小题给出的四个选项中,只有一个项是符合题目要求的)
1.指数函数y=ax的图像经过点(2,16)则a的值是 ( )
A. B. C.2 D.4
2.化简的结果 ( )
A. B. C. D.
3.在区间上不是增函数的是 ( )
A. B.
C. D.
4.式子的值为 ( )
(A) (B) (C) (D)
5.已知,下面四个等式中:
①; ②;
③ ; ④.
其中正确命题的个数为 ( )
A.0 B.1 C.2 D.3
6. 已知,,,则三者的大小关系是 ( )
A. B. C. D.
7.已知函数的反函数,则方程的
解集是( )
A.{1} B.{2} C.{3} D.{4}
8.设,则使为奇函数且在(0,+)上单调递减的值的个数为 ( )
A. 1 B. 2 C. 3 D. 4
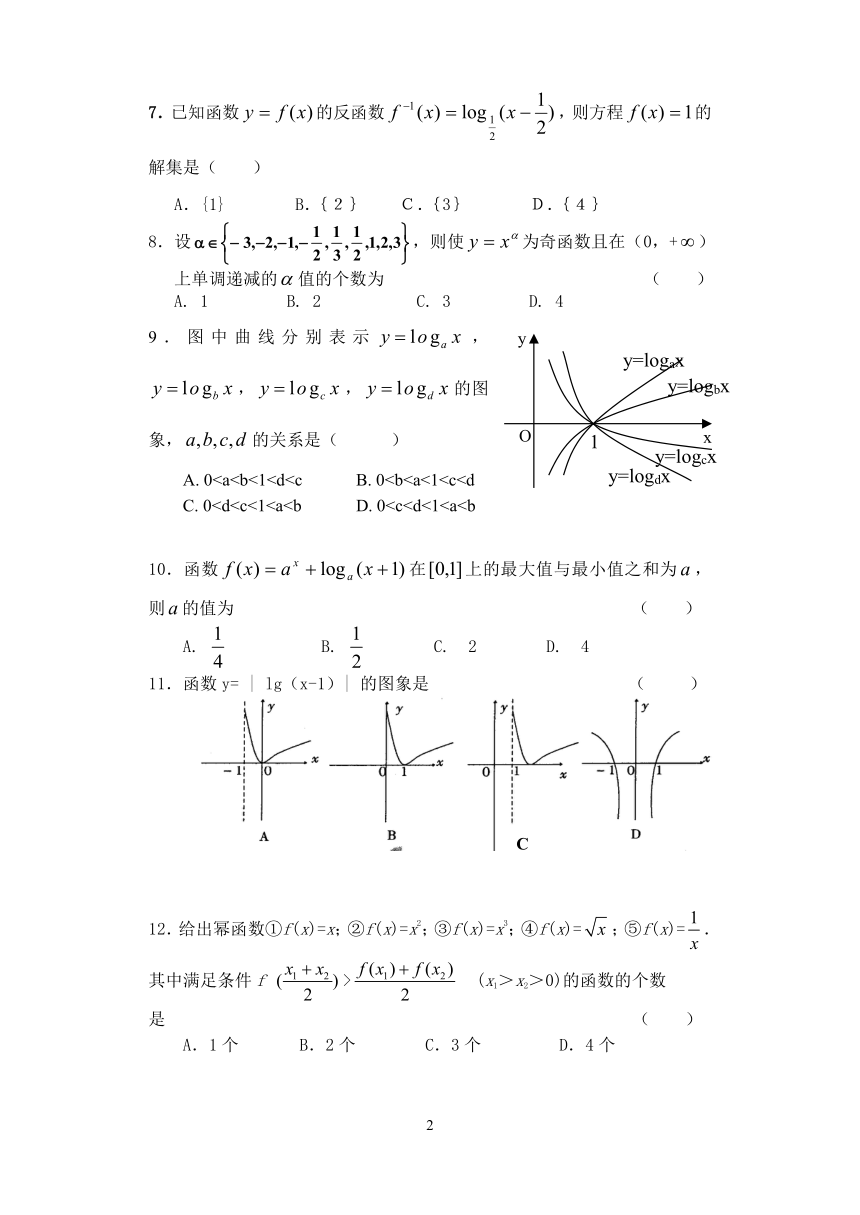
9.图中曲线分别表示,,,的图象,的关系是( )
A. 0C. 010.函数在上的最大值与最小值之和为,则的值为 ( )
A. B. C. 2 D. 4
11.函数y= | lg(x-1)| 的图象是 ( )
12.给出幂函数①f(x)=x;②f(x)=x2;③f(x)=x3;④f(x)=;⑤f(x)=.
其中满足条件f > (x1>x2>0)的函数的个数
是 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(.每小题4分,共16分)
13.函数的定义域是 .
14.当a>0且a≠1时,函数f (x)=ax-2-3必过定点 .
15.函数的单调递减区间是_________________.
16.关于函数有下列命题:
①函数的图象关于轴对称; ②在区间上,函数是减函数;③函数的最小值为; ④在区间上,函数是增函数.
其中正确命题序号为_______________.
三、解答题(6小题,共74分)
17.(本小题满分12分)
18. (本小题满分12分)
设函数, 求满足=的x的值.
19.(本小题满分12分)
已知,是一次函数,并且点在函数的图象上,点在函数的图象上,求的解析式.
20.(本小题满分12分)
若0≤x≤2,求函数y=的最大值和最小值.
21.(本小题满分12分)
光线通过一块玻璃,其强度要损失,把几块这样的玻璃重叠起来,设
光线原来的强度为,通过块玻璃后强度为.
(1)写出关于的函数关系式;
(2)通过多少块玻璃后,光线强度减弱到原来的以下 (
22. (本小题满分14分)已知定义域为的函数是奇函数。
(Ⅰ)求的值;
(Ⅱ)判断函数的单调性;
(Ⅲ)若对任意的,不等式恒成立,求的取值范围.
上杭县2007—2008学年第一学期高一数学单元卷(二)A
参考答案
(内容:必修1第二章基本初等函数)
一、选择题
1.D 由a=16且a>0得a=4
2.C 解:原式
3.C 根据反比例函数性质
4.A log9= 原式=
5.B ab>0 a、b同号。当a、b同小于0时①②不成立;
当ab=1时④不成立,故只有③对。
6.A a<0,b>1 , 07.A 根据互为反函数的性质得x=f(1)=log(1-)=1
8. B 根据幂函数性质得取-3,-1两个
9.D 作直线y=1与四条曲线交点的横坐标即为对应函数的底数。
10.B 函数f(x)在区间端点0、1处取到最大值与最小值
f(0)+f(1)=a 得a=
11.C x>1,y0
12.A 画出各函数图象,设直线x=x,x=x与图象交点分别为A、B则
f(为弧线段与直线x=的交点函数值,为线段AB中点函数值。观察各图象可知④正确
二、填空题:
13. x>2且x3
14.(2,-2) 函数y=a过定点(0,1),利用平移求得
15. x-2x>0 x>2或x<0, 又对数函数的底数<1 原函数的递减区间即为二次函数y=x-2x的递增区间
16.①③④ f(x)=lg(+)是偶函数 ①正确
又函数y=+在区间(﹣∞,-1)上递减,在区间(﹣1,0)上递增,根据复合函数单调性知(2)错,④正确,由单调性知函数y=+在x=时y有最小值2 ③正确
三、解答题
17.原式=………6分
=22×33+2 — 7— 2— 1 ………10分
=100 ………12分
18.解:当x∈(﹣∞,1)时,由2﹣x=,得x=2,但2(﹣∞,1),舍去。
………5分
当x∈(1,+∞)时,由log4x=,得x=,∈(1,+∞)。………10分
综上所述,x= ………12分
19. 解: g(x)是一次函数 ∴可设g(x)=kx+b (k0)
∴f=2 g=k2+b ………4分
∴依题意得 ………6分
即 ………10分 ∴.………12分
20. 解: ………2分
令,因为0≤x≤2,所以 ………4分
则y== ()
因为二次函数的对称轴为t=3,所以函数y=在区间[1,3]上是减函数,在区间[3,4]上是增函数. ………7分
∴ 当,即x=log3时 ………10分
当,即x=0时 ………12分
21.解析: (1) ………4分
(2) ………8分
………10分 ∴ . ………12分
22.Ⅰ)因为是奇函数,所以=0,
即………………………..3分
(Ⅱ)由(Ⅰ)知,
设则
因为函数y=2在R上是增函数且 ∴>0
又>0 ∴>0即
∴在上为减函数。 ……………8分
(Ⅲ)因是奇函数,从而不等式:
等价于,………….10分
因为减函数,由上式推得:.即对一切有:, ………………….12分
从而判别式 ……….14分
x
y
O
y=logax
y=logbx
y=logcx
y=logdx
1
C
PAGE
1
(内容:必修1第二章基本初等函数)
(满分:150分;考试时间:100分钟)
一、选择题(本大题共12小题. 每小题5分,共60分。 在每小题给出的四个选项中,只有一个项是符合题目要求的)
1.指数函数y=ax的图像经过点(2,16)则a的值是 ( )
A. B. C.2 D.4
2.化简的结果 ( )
A. B. C. D.
3.在区间上不是增函数的是 ( )
A. B.
C. D.
4.式子的值为 ( )
(A) (B) (C) (D)
5.已知,下面四个等式中:
①; ②;
③ ; ④.
其中正确命题的个数为 ( )
A.0 B.1 C.2 D.3
6. 已知,,,则三者的大小关系是 ( )
A. B. C. D.
7.已知函数的反函数,则方程的
解集是( )
A.{1} B.{2} C.{3} D.{4}
8.设,则使为奇函数且在(0,+)上单调递减的值的个数为 ( )
A. 1 B. 2 C. 3 D. 4
9.图中曲线分别表示,,,的图象,的关系是( )
A. 0
A. B. C. 2 D. 4
11.函数y= | lg(x-1)| 的图象是 ( )
12.给出幂函数①f(x)=x;②f(x)=x2;③f(x)=x3;④f(x)=;⑤f(x)=.
其中满足条件f > (x1>x2>0)的函数的个数
是 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(.每小题4分,共16分)
13.函数的定义域是 .
14.当a>0且a≠1时,函数f (x)=ax-2-3必过定点 .
15.函数的单调递减区间是_________________.
16.关于函数有下列命题:
①函数的图象关于轴对称; ②在区间上,函数是减函数;③函数的最小值为; ④在区间上,函数是增函数.
其中正确命题序号为_______________.
三、解答题(6小题,共74分)
17.(本小题满分12分)
18. (本小题满分12分)
设函数, 求满足=的x的值.
19.(本小题满分12分)
已知,是一次函数,并且点在函数的图象上,点在函数的图象上,求的解析式.
20.(本小题满分12分)
若0≤x≤2,求函数y=的最大值和最小值.
21.(本小题满分12分)
光线通过一块玻璃,其强度要损失,把几块这样的玻璃重叠起来,设
光线原来的强度为,通过块玻璃后强度为.
(1)写出关于的函数关系式;
(2)通过多少块玻璃后,光线强度减弱到原来的以下 (
22. (本小题满分14分)已知定义域为的函数是奇函数。
(Ⅰ)求的值;
(Ⅱ)判断函数的单调性;
(Ⅲ)若对任意的,不等式恒成立,求的取值范围.
上杭县2007—2008学年第一学期高一数学单元卷(二)A
参考答案
(内容:必修1第二章基本初等函数)
一、选择题
1.D 由a=16且a>0得a=4
2.C 解:原式
3.C 根据反比例函数性质
4.A log9= 原式=
5.B ab>0 a、b同号。当a、b同小于0时①②不成立;
当ab=1时④不成立,故只有③对。
6.A a<0,b>1 , 0
8. B 根据幂函数性质得取-3,-1两个
9.D 作直线y=1与四条曲线交点的横坐标即为对应函数的底数。
10.B 函数f(x)在区间端点0、1处取到最大值与最小值
f(0)+f(1)=a 得a=
11.C x>1,y0
12.A 画出各函数图象,设直线x=x,x=x与图象交点分别为A、B则
f(为弧线段与直线x=的交点函数值,为线段AB中点函数值。观察各图象可知④正确
二、填空题:
13. x>2且x3
14.(2,-2) 函数y=a过定点(0,1),利用平移求得
15. x-2x>0 x>2或x<0, 又对数函数的底数<1 原函数的递减区间即为二次函数y=x-2x的递增区间
16.①③④ f(x)=lg(+)是偶函数 ①正确
又函数y=+在区间(﹣∞,-1)上递减,在区间(﹣1,0)上递增,根据复合函数单调性知(2)错,④正确,由单调性知函数y=+在x=时y有最小值2 ③正确
三、解答题
17.原式=………6分
=22×33+2 — 7— 2— 1 ………10分
=100 ………12分
18.解:当x∈(﹣∞,1)时,由2﹣x=,得x=2,但2(﹣∞,1),舍去。
………5分
当x∈(1,+∞)时,由log4x=,得x=,∈(1,+∞)。………10分
综上所述,x= ………12分
19. 解: g(x)是一次函数 ∴可设g(x)=kx+b (k0)
∴f=2 g=k2+b ………4分
∴依题意得 ………6分
即 ………10分 ∴.………12分
20. 解: ………2分
令,因为0≤x≤2,所以 ………4分
则y== ()
因为二次函数的对称轴为t=3,所以函数y=在区间[1,3]上是减函数,在区间[3,4]上是增函数. ………7分
∴ 当,即x=log3时 ………10分
当,即x=0时 ………12分
21.解析: (1) ………4分
(2) ………8分
………10分 ∴ . ………12分
22.Ⅰ)因为是奇函数,所以=0,
即………………………..3分
(Ⅱ)由(Ⅰ)知,
设则
因为函数y=2在R上是增函数且 ∴>0
又>0 ∴>0即
∴在上为减函数。 ……………8分
(Ⅲ)因是奇函数,从而不等式:
等价于,………….10分
因为减函数,由上式推得:.即对一切有:, ………………….12分
从而判别式 ……….14分
x
y
O
y=logax
y=logbx
y=logcx
y=logdx
1
C
PAGE
1
