人教版高一数学下学期必修第二册第十章《概率》单元达标高分突破培优卷(含解析)
文档属性
| 名称 | 人教版高一数学下学期必修第二册第十章《概率》单元达标高分突破培优卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 618.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-17 10:12:16 | ||
图片预览




文档简介
人教版高一数学下学期必修第二册第十章《概率》单元达标高分突破培优卷
一、单项选择题:本题共8小题,每小题满分5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求,选对得5分,选错得0分.
1.下列事件:①任取一个整数,被2整除;②小明同学在某次数学测试中成绩一定不低于120分;③甲、乙两人进行竞技比赛,甲的实力远胜于乙,在一次比赛中甲一定获胜;④当圆的半径变为原来的2倍时,圆的面积是原来的4倍.其中随机事件的个数是( )
A.1 B.3 C.0 D.4
2.(贵州省镇远县文德民族中学校2021届高三11月月考数学(理)试题)按文献记载,《百家姓》成文于北宋初年,表1记录了《百家姓》开头的24大姓氏:
表1
赵 钱 孙 李 周 吴 郑 王 冯 陈 褚 卫
蒋 沈 韩 杨 朱 秦 尤 许 何 吕 施 张
表2记录了2018年中国人口最多的前25大姓氏:
表2
1:李 2:王 3:张 4:刘 5:陈
6:杨 7:赵 8:黄 9:周 10:吴
11:徐 12:孙 13:胡 14:朱 15:高
16:林 17:何 18:郭 19:马 20:罗
21:梁 22:宋 23:郑 24:谢 25:韩
从《百家姓》开头的24大姓氏中随机选取1个姓氏,则该姓氏是2018年中国人口最多的前24大姓氏的概率为( )A. B. C. D.
3.(湖南省邵阳市邵东县第一中学2019-2020学年高二下学期第一次月考数学试题)下列说法错误的是( )
A.任一事件的概率总在内 B.不可能事件的概率一定为0
C.必然事件的概率一定为1 D.概率是随机的,在试验前不能确定
4.(2022·江西·南昌十中高一期中)甲、乙去同一家药店购买一种医用外科口罩,已知这家药店出售A,B,C三种医用外科口罩,甲、乙购买A,B,C三种医用口罩的概率分别如表:
购买A种医用口罩 购买B种医用口罩 购买C种医用口罩
甲 0.1 0.4
乙 0.3 0.2
则甲、乙购买的是同一种医用外科口罩的概率为( )
A.0.24 B.0.28 C.0.30 D.0.32
5.(10.1.2事件的关系和运算-2020-2021学年高一数学新教材配套学案(人教A版2019必修第二册))从1,2,3,…,7这7个数中任取两个数,其中:
①恰有一个是偶数和恰有一个是奇数;②至少有一个是奇数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数.
上述事件中,是对立事件的是( )
A.① B.②④ C.③ D.①③
6.(陕西省黄陵中学2016-2017学年高一(普通班)下学期期末考试数学试题)从某班学生中任意找出一人,如果该同学的身高小于160 cm的概率为0.2,该同学的身高在[160,175](单位:cm)内的概率为0.5,那么该同学的身高超过175 cm的概率为( )
A.0.2 B.0.3 C.0.7 D.0.8
7.(重庆市南开中学2020届高三下学期第九次教学质量检测数学(理)试题)据《孙子算经》中记载,中国古代诸侯的等级从低到高分为:男 子 伯,侯 公,共五级.若给有巨大贡献的3人进行封爵,假设每种封爵的可能性相等,则3人中恰好有两人被封同一等级的概率为( )
A. B. C. D.
8.(山东省德州市2019-2020学年高二下学期期末考试数学试题)甲、乙两队进行友谊赛,采取三局两胜制,每局都要分出胜负,根据以往经验,单局比赛中甲队获胜的概率为,设各局比赛相互间没有影响,则甲队战胜乙队的概率为( )
A. B. C. D.
多项选择题:本题共4小题,每小题满分5分,共20分. 在每小题给出的四个选项中,有多项符合题目要求。全部选对得5分,部分选对得2分,有选错的得0分.
9.下列命题中是真命题的是( )
A.做7次抛掷一枚均匀硬币的试验,结果有4次出现正面,因此出现正面的概率是
B.盒子中有大小均匀的3个黑球,2个白球,1个红球,则每种颜色被摸到的可能性相同
C.从-4,-3,-2,-1,0,1,2中任取一个数,取得小于0的概率大于取得不小于0的概率
D.分别从2名男生,2名女生中各选一名作为代表,则每名学生被选中的可能性相同
10.(第十章概率10.1随机事件与概率10.1.4概率的基本性质)黄种人群中各种血型的人所占的比例见下表:
血型 A B AB O
该血型的人所占比例 0.28 0.29 0.08 0.35
已知同种血型的人可以输血,O型血可以给任何一种血型的人输血,任何血型的人都可以给血型的人输血,其他不同血型的人不能互相输血,下列结论正确的是( )
A.任找一个人,其血可以输给B型血的人的概率是0.64
B.任找一个人,B型血的人能为其输血的概率是0.29
C.任找一个人,其血可以输给O型血的人的概率为1
D.任找一个人,其血可以输给型血的人的概率为1
11.(2021·河北保定·高一期末)以下结论不正确的是( )
A.对立事件一定互斥 B.事件A与事件B的和事件的概率一定大于事件A的概率
C.事件A与事件B互斥,则有 D.事件A,B满足,则A,B是对立事件
12.(2021·湖南·衡阳市八中高一期末)4支足球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.下列结论中正确的是( )
A.恰有四支球队并列第一名为不可能事件 B.有可能出现恰有三支球队并列第一名
C.恰有两支球队并列第一名的概率为 D.只有一支球队名列第一名的概率为
填空题:本题共4小题,每小题5分,共20分。
13.(2022·江西·景德镇一中高一期末)某次联欢会上设有一个抽奖游戏,抽奖箱中共有四种不同颜色且形状大小完全相同的小球16个,分别代表一等奖、二等奖、三等奖、无奖四种奖项.其中红球代表一等奖且只有1个,黄球代表三等奖,从中任取一个小球,若中二等奖或三等奖的概率为,小华同学获得一次摸奖机会,则求他不能中奖的概率是____________.
14.(2022·陕西·宝鸡市陈仓区教育体育局教学研究室高一期中)给出如下几个命题:
①若A是随机事件,则;
②若事件A与B是互斥事件,则A与B一定是对立事件;
③若事件A与B是对立事件,则A与B一定是互斥事件;
④事件A,B中至少有一个发生的概率一定比A,B中恰有一个发生的概率大.
其中正确的是___________.(填序号)
15.(2019年浙江省十校联盟高三上学期10月联考数学试题)1742年6月7日,哥德巴赫在给大数学家欧拉的信中提出:任一大于2的偶数都可写成两个质数的和.这就是著名的“哥德巴赫猜想”,可简记为“1+1”.1966年,我国数学家陈景润证明了“1+2”,获得了该研究的世界最优成果.若在不超过30的所有质数中,随机选取两个不同的数,则两数之和不超过30的概率是________.
16.(2018·山西·怀仁市第一中学校高一期末)口袋里装有1红,2白,3黄共6个形状相同的小球,从中取出2球,事件“取出的两球同色”,“取出的2球中至少有一个黄球”,“取出的2球至少有一个白球”,“取出的两球不同色”,“取出的2球中至多有一个白球”.下列判断中正确的序号为________.
①与为对立事件;②与是互斥事件;③与是对立事件:④;⑤.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(陕西省渭南市华州区咸林中学2021-2022学年高二下学期期中理科数学试题)甲 乙两人参加一次考试.已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题,规定每次考试都从各选题中随机抽出3题进行测试,至少答对2题才算合格.
(1)分别求甲 乙两人考试合格的概率;
(2)求甲 乙两人至少有一人考试合格的概率.
18.国家规定每年的月日以后的天为当年的暑假.某钢琴培训机构对位钢琴老师暑假一天的授课量进行了统计,如下表所示:
授课量(单位:小时)
频数
培训机构专业人员统计近年该校每年暑假天的课时量情况如下表:
课时量(单位:天)
频数
(同组数据以这组数据的中间值作代表)
(1)估计位钢琴老师一日的授课量的平均数;
(2)若以(1)中确定的平均数作为上述一天的授课量.已知当地授课价为元/小时,每天的各类生活成本为元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师天暑假授课利润不少于万元的概率.
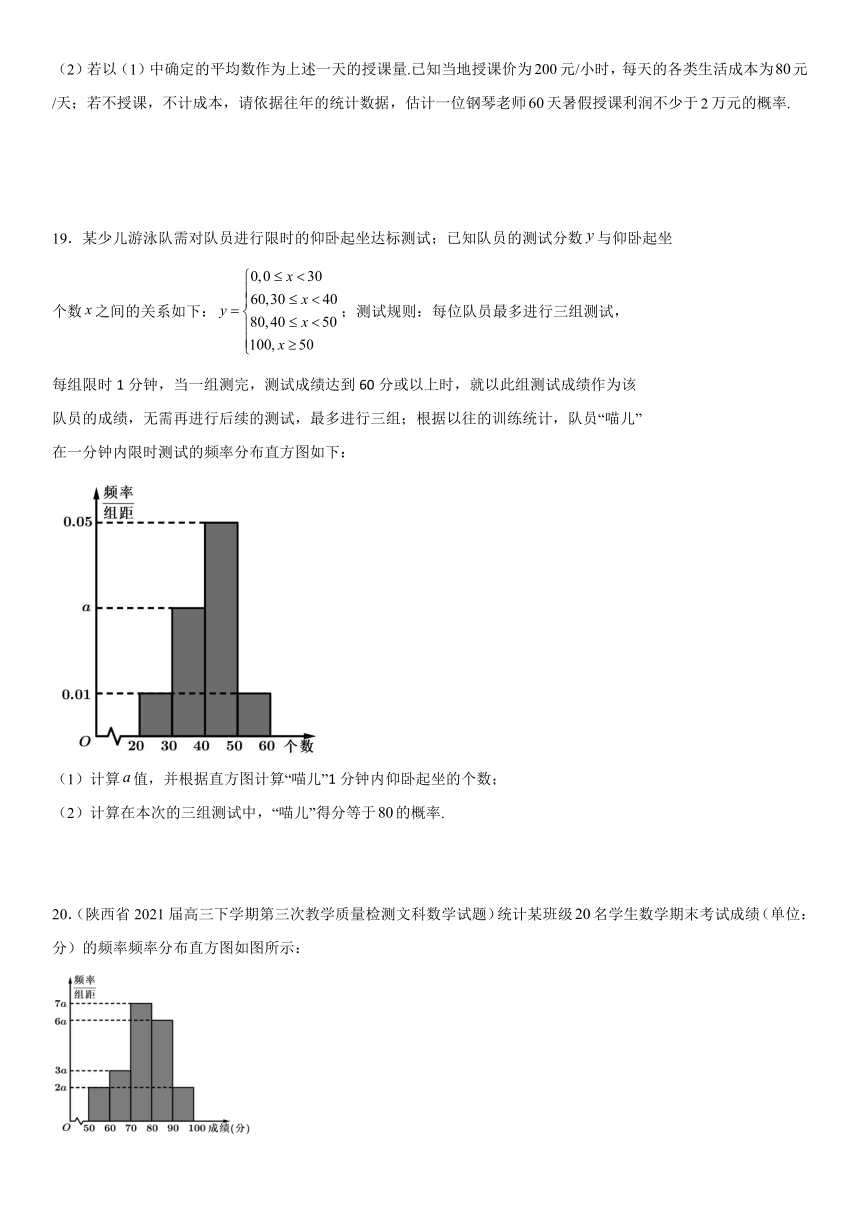
19.某少儿游泳队需对队员进行限时的仰卧起坐达标测试;已知队员的测试分数与仰卧起坐
个数之间的关系如下:;测试规则:每位队员最多进行三组测试,
每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该
队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”
在一分钟内限时测试的频率分布直方图如下:
(1)计算值,并根据直方图计算“喵儿”1分钟内仰卧起坐的个数;
(2)计算在本次的三组测试中,“喵儿”得分等于的概率.
20.(陕西省2021届高三下学期第三次教学质量检测文科数学试题)统计某班级名学生数学期末考试成绩(单位:分)的频率频率分布直方图如图所示:
(1)分别求出成绩落在与中的学生人数;
(2)从成绩在和的学生中按照分层抽样的方法抽取人参加全校数学文化知识竞赛,如果有人获奖,求这人的成绩都在中的概率.
21.(2021·河北邯郸·高一期末)某市为了了解人们对“中国梦”的伟大构想的认知程度,针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(95分及以上为认知程度高),结果认知程度高的有人,按年龄分成5组,其中第一组:,第二组:,第三组:,第四组:,第五组:,得到如图所示的频率分布直方图,已知第一组有10人.
(1)根据频率分布直方图,估计这人的平均年龄和第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任本市的“中国梦”宣传使者.
(i)若有甲(年龄38),乙(年龄40)两人已确定人选宣传使者,现计划从第四组和第五组被抽到的使者中,再随机抽取2名作为组长,求甲、乙两人至少有一人被选上的概率;
(ii)若第四组宣传使者的年龄的平均数与方差分别为37和,第五组宣传使者的年龄的平均数与方差分别为43和1,据此估计这人中35~45岁所有人的年龄的方差.
22.(2020·山东·胶州市教育和体育局高一期末)有一种鱼的身体吸收汞,当这种鱼身体中的汞含量超过其体重的(即百万分之一)时,人食用它,就会对人体产生危害.现从一批该鱼中随机选出条鱼,检验鱼体中的汞含量与其体重的比值(单位:),数据统计如下:
(1)求上述数据的中位数、众数、极差,并估计这批鱼该项数据的分位数;
(2)有,两个水池,两水池之间有个完全相同的小孔联通,所有的小孔均在水下,且可以同时通过条鱼.
(ⅰ)将其中汞的含量最低的条鱼分别放入水池和水池中,若这条鱼的游动相互独立,均有的概率进入另一水池且不再游回,求这两条鱼最终在同一水池的概率;
(ⅱ)将其中汞的含量最低的条鱼都先放入水池中,若这条鱼均会独立地且等可能地从其中任意一个小孔由水池进入水池且不再游回水池,求这两条鱼由不同小孔进入水池的概率.
参考答案全解全析
1.B
【详解】
①②③均是可能发生也可能不发生的事件,为随机事件,
④是一定发生的事件,为必然事件.
则随机事件有个.
故选:B.
2.C
【详解】
因为从《百家姓》开头的24大姓氏中随机选取1个姓氏的基本事件共有24种,
2018年中国人口最多的前24大姓氏中《百家姓》开头的24大姓氏的基本事件有赵、孙、李、周、吴、郑、王、陈、杨、朱、何、张共有12种,
所以该姓氏是2018年中国人口最多的前24大姓氏的概率为概率为,
故选:C
3.D
解:任一事件的概率总在内,不可能事件的概率为0,必然事件的概率为1,概率是客观存在的,是一个确定值.
故选:D.
4.B
由概率的性质求得甲购买A口罩、乙购买B口罩的概率,再应用独立事件乘法公式和互斥事件加法公式求概率.
【详解】
由表知:甲购买A口罩概率为,乙购买B口罩概率为,
所以甲、乙购买同一种口罩的概率.
故选:B
5.C
【详解】
解析:③中“至少有一个是奇数”即“两个奇数或一奇一偶”,
而从1~7中任取两个数根据取到数的奇偶性可认为共有三件事件:
“两个都是奇数”“一奇一偶”“两个都是偶数”,
故“至少有一个是奇数”与“两个都是偶数”是对立事件,其余都不是对立事件.
故选:C
6.B
解:因为该同学的身高小于160cm的概率为0.2,该同学的身高在[160,175]cm的概率为0.5,和该同学的身高超过175cm的概率和为1,利用对立事件可知1-0.2-0.5=0.3,选B
7.D
【解析】
先由题意,确定3人封爵所包含的总的基本事件个数,再求出满足条件的基本事件个数,基本事件个数比,即可为所求概率.
【详解】
由题意,每个人被封爵都有5种情况,因此对3人封爵,共有种,
3人中恰好有两人被封同一等级共有种情况;
则3人中恰好有两人被封同一等级的概率为.
故选:D.
【点睛】
本题主要考查求古典概型的概率,属于常考题型.
8.C
【解析】
【分析】
甲队战胜乙队包含两种情况:①甲连胜2局,②前两局甲队一胜一负,第三局甲队胜,由此利用相互独立事件概率乘法公式和互斥事件概率加法公式能求出甲队战胜乙队的概率.
【详解】
甲、乙两队进行友谊赛,采取三局两胜制,每局都要分出胜负,
根据以往经验,单局比赛中甲队获胜的概率为,设各局比赛相互间没有影响,
甲队战胜乙队包含两种情况:
①甲连胜2局,概率为,
②前两局甲队一胜一负,第三局甲队胜,概率为,
则甲队战胜乙队的概率为.
故选:.
【点睛】
本题考查概率的求法,考查相互独立事件概率乘法公式和互斥事件概率加法公式等基础知识,考查推理能力与计算能力,是基础题.
9.CD
【解析】
【分析】
根据题意求出各试验事件发生的概率,逐一判断即可得出选项.
【详解】
解析:A中,抛掷一枚硬币出现正面的概率是,故错误;
B中,摸到黑球 白球 红球的可能性分别为,,,故错误,
C中,取得小于0的概率为,取得不小于0的概率为,故正确;
D中,每名学生被选中的可能性都为,故正确.
故选:CD.
10.AD
【解析】
根据输血的规则,可以输给B型血的人为B或O型;B型血的人可以输血给B型或血型;可以输给O型血的人只能是O型;所有人都可以输给型血的人.
【详解】
任找一个人,其血型为A、B、、O型血的事件分别记为、、、,它们两两互斥.
由已知,有,,,.因为B,O型血可以输给B型血的人,
所以“可以输给B型血的人”为事件,根据概率的加法公式,得,故A正确;
B型血的人能为B型、型的人输血,其概率为,B错误;
由O型血只能接受O型血的人输血知,C错误;
由任何人的血都可以够给型血的人,知D正确.
故选:AD.
【点睛】
此题考查互斥事件概率加法公式,关键在于弄清题意,此题应弄清楚可以输血的规则.
11.BCD
【解析】
【分析】
由对立事件与互斥事件的关系可判断A;由事件的包含关系可判断B;由对立事件的概率可判断C;由对立事件的定义可判断D.
【详解】
对于选项A:对立事件一定是互斥事件,故A正确;
对于选项B:当事件包含事件时,事件A与事件B的和事件的概率等于事件A的概率,故B错误;
对于选项C:当事件A与事件B对立时,则有,因为互斥事件不一定是对立事件,故C错误;
对于选项D:由对立事件的定义可知这种说法是错误的. 故D错误.
故选:BCD.
12.ABD
【解析】
【分析】
4支足球队进行单循环比赛总的比赛共有场比赛,比赛的所有结果共有种;
选项A,这6场比赛中不满足4支球队得分相同的的情况;
选项B,举特例说明即可;
选项C,在6场比赛中,从中选2支球队并列第一名有种可能,再分类计数相互获胜的可能数,最后由古典概型计算概率;
选项D,只有一支球队名列第一名,则该球队应赢了其他三支球队,由古典概型问题计算即可.
【详解】
4支足球队进行单循环比赛总的比赛共有场比赛,比赛的所有结果共有种;
选项A,这6场比赛中若4支球队优先各赢一场,则还有2场必然有2支或1支队伍获胜,那么所得分值不可能都一样,故是不可能事件,正确;
选项B,其中6场比赛中,依次获胜的可以是,此时3队都获得2分,并列第一名,正确;
选项C,在6场比赛中,从中选2支球队并列第一名有种可能,若选中a,b,其中第一类a赢b,有a,b,c,d,a,b和a,b,d,c,a,b两种情况,同理第二类b赢a,也有两种,故恰有两支球队并列第一名的概率为,错误;
选项D,从4支球队中选一支为第一名有4种可能;这一支球队比赛的3场应都赢,则另外3场的可能有种,故只有一支球队名列第一名的概率为,正确.
故选:ABD
【点睛】
本题考查利用计数原理解决实际问题的概率问题,还考查了事件成立与否的判定,属于较难题.
13.
【详解】
从个球中任取一个小球,中二等奖或三等奖的概率为,
故可得代表二等奖和三等奖的球共有个,又代表一等奖的球有个,
故代表无奖的球有个,故小华同学获得一次摸奖机会,不能中奖的概率.
故答案为:.
14.① ③
【解析】
【分析】
由几何概型中随机事件的发生概率可以为0或1,判断①;若事件A与B是对立事件,则A与B一定是互斥事件,但事件A与B是互斥事件,则A与B不一定是对立事件,判断②、③;当A与B的发生概率为0或A与B互斥时,则事件A,B中至少有一个发生的概率不一定与A,B中恰有一个发生的概率相同,判断④.
【详解】
若A是随机事件,则,在几何概型中随机事件的发生概率可以为0或1,故①正确;
但事件A与B是互斥事件,则A与B不一定是对立事件;例如掷一枚骰子“朝上的面为1”和“朝上的面为2”互斥但不对立,故②错误、
若事件A与B是对立事件,则A与B一定是互斥事件,互斥事件包含对立事件;故③正确;
事件A,B中至少有一个发生的概率不一定比A,B中恰有一个发生的概率大,如果A与B的发生概率为0或A与B互斥,则概率一样大,故④错误.
故答案为:① ③
15.
【解析】
【分析】
根据题意,利用列举法求出不超过30的所有质数,再利用古典概型的概率公式进行计算即可.
【详解】
根据题意可知,不共有超过30的所有质数有2,3,5,7,11,13,17,19,23,29共10个,从中选取2个不同的数有种,和超过30的共有15种,所以两数之和不超过30的概率是.
【点睛】
本题主要考查古典概型概率的求解.
16.①④
【解析】
【分析】
在①中,由对立事件定义得与为对立事件;有②中,与有可能同时发生;在③中,与有可能同时发生;在④中,(C)(E);在⑤中,从而(B)(C).
【详解】
口袋里装有1红,2白,3黄共6个形状相同小球,从中取出2球,
事件 “取出的两球同色”, “取出的2球中至少有一个黄球”,
“取出的2球至少有一个白球”, “取出的两球不同色”, “取出的2球中至多有一个白球”,
①,由对立事件定义得与为对立事件,故①正确;
②,与有可能同时发生,故与不是互斥事件,故②错误;
③,与有可能同时发生,不是对立事件,故③错误;
④,(C),(E),,
从而(C)(E),故④正确;
⑤,,从而(B)(C),故⑤错误.
故答案为:①④.
【点睛】
本题考查命题真假的判断,是基础题,考查对立互斥事件,解题时要认真审题,注意对立事件、互斥事件等基本概念的合理运用.
17.(1)甲 乙两人考试合格的概率分别为、;
(2).
【解析】
【分析】
(1)根据古典概型计算公式进行求解即可;
(2)根据(1)的结论,结合对立事件的概率公式进行求解即可.
(1)
设事件:甲考试合格,事件:乙考试合格,
所以,;
(2)
甲 乙两人至少有一人考试合格的概率为:.
18.(1)小时;(2).
【解析】
(1)将每组的中点值乘以频数,相加后除以可得出位老师暑假一日的授课量的平均数;
(2)设一位钢琴老师每年暑假天的授课天数为,计算出每位钢琴老师每日的利润,结合每位钢琴老师天暑假授课利润不少于万元求得的取值范围,再结合课时量频数表可得出所求事件的概率.
【详解】
(1)估计位老师暑假一日的授课量的平均数为小时;
(2)设每年暑假天的授课天数为,则利润为.
由,得.
一位老师暑假利润不少于万元,即授课天数不低于天,
又天暑假内授课天数不低于天的频率为.
预测一位老师天暑假授课利润不少于万元的概率为.
【点睛】
本题考查频数分布表的应用,考查平均数与概率的计算,考查数据处理能力,属于基础题.
19.(1)0.03;41个;(2)0.555.
【解析】
【分析】
(1)由可得,利用每个矩形的中点横坐标与该矩形的纵坐标相乘后求和,即可结果;(2)在本次的三组测试中,“喵儿”得分为事件A,则“喵儿”可能第一组得分,或者第二组得分,或者第三组得分,根据互斥事件的概率公式以及独立事件同时发生的概率公式可得结果.
【详解】
(1).
“喵儿”仰卧起坐的平均值为:(个)
(2)由直方图可知,“喵儿”的得分情况如下:
0 60 80 100
0.1 0.5 0.1
在本次的三组测试中,“喵儿”得80分为事件A,则“喵儿”可能第一组得80分,或者第二组得80
分,或者第三组得80分,则.
【点睛】
本题主要考查频率分布直方图的应用,以及互斥事件与独立事件的概率公式,属于中档题. 直方图的主要性质有:(1)直方图中各矩形的面积之和为;(2)组距与直方图纵坐标的乘积为该组数据的频率;(3)每个矩形的中点横坐标与该矩形的纵坐标相乘后求和可得平均值;(4)直观图左右两边面积相等处横坐标表示中位数.
20.(1)成绩落在中学生人数为,成绩落在中学生人数为;(2).
【解析】
【分析】
(1)根据频率分布直方图中所有矩形面积之和为求出实数的值,并计算出成绩落在与中的学生所占的频率,乘以可得结果;
(2)列出所有的基本事件,并确定事件“所抽的人的成绩都在中”所包含的基本事件数,利用古典概型的概率公式可求得所求事件的概率.
【详解】
(1)据直方图知组距为,由,解得,
成绩落在中学生人数为,
成绩落在中学生人数为;
(2)从成绩在和的学生中按照分层抽样的方法抽取人,成绩落在有人,成绩落在有人,
记成绩落在中的人为、,成绩落在中的人为、、、,
则从人选人的基本事件共有个:
、、、、、、、、、、、、、、.
其中人的成绩都在中的基本事件有6个.
故所求概率为.
【点睛】
方法点睛:求解古典概型概率的方法如下:
(1)列举法;
(2)列表法;
(3)数状图法;
(4)排列组合数的应用.
21.(1)32.25岁;37.5;(2)(i);(ii)10.
【解析】
【分析】
(1) 根据频率分布直方图,利用组中值乘以相应的频率,即可的这人的平均年龄;设第80百分位数为,计算从左到右频率和为或计算从右到左频率和为,即可求出;
(2)(i)由题意可得,第四组应抽取4人,记为,,,甲,第五组抽取2人,记为,乙,根据古典概型计算方法求解即可;
(ii)根据方差的计算原理计算合并后方差即可.
【详解】
解:(1)设这人的平均年龄为,则
(岁).
设第80百分位数为,
方法一:由,解得.
方法二:由,解得.
(2)(i)由题意得,第四组应抽取4人,记为,,,甲,第五组抽取2人,记为,乙,
对应的样本空间为:
,共15个样本点.
设事件“甲、乙两人至少一人被选上”,则
,共有9个样本点.
所以,.
(ii)设第四组、第五组的宣传使者的年龄的平均数分别为,,方差分别为,,
则,,,,
设第四组和第五组所有宣传使者的年龄平均数为,方差为.
则,
,
因此,第四组和第五组所有宣传使者的年龄方差为10,
据此,可估计这人中年龄在35~45岁的所有人的年龄方差约为10.
22.(1)中位数为;众数为;极差为;估计这批鱼该项数据的百分位数约为;(2)(ⅰ);(ⅱ).
【解析】
【分析】
(1)由中位数—排序后处于中间的数,如有两个数取其平均数;众数—出现频率最高的数、极差—最大数与最小数的差;百分比位数—数据集中有n个数:当np为整数时,当np不为整数时;即可求出对应值;(2) (ⅰ)记:“两鱼最终均在水池”; :“两鱼最终均在水池”求出概率,由它们的互斥性即可求得两条鱼最终在同一水池的概率;(ⅱ)记:“两鱼同时从第n个小孔通过”且鱼的游动独立,知,而10个事件互斥,则“两鱼同时从一个小孔通过”的概率即可求,它与“两条鱼由不同小孔通过”为互斥事件,进而求得其概率
【详解】
解:(1)由题意知,数据的中位数为
数据的众数为
数据的极差为
估计这批鱼该项数据的百分位数约为
(2)(ⅰ)记“两鱼最终均在水池”为事件,则
记“两鱼最终均在水池”为事件,则
∵事件与事件互斥,
∴两条鱼最终在同一水池的概率为
(ⅱ)记“两鱼同时从第一个小孔通过”为事件,“两鱼同时从第二个小孔通过”为
事件,依次类推;而两鱼的游动独立
∴
记“两条鱼由不同小孔进入水池”为事件,则与对立,又由事件,事件,互斥
∴
即
【点睛】
本题考查了数据特征值的概念,以及利用条件概率公式,结合互斥事件、独立事件等概念求概率;注意独立事件:多个事件的发生互不相关,且可以同时发生;互斥事件:一个事件发生则另一个事件必不发生,即不能同时发生
一、单项选择题:本题共8小题,每小题满分5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求,选对得5分,选错得0分.
1.下列事件:①任取一个整数,被2整除;②小明同学在某次数学测试中成绩一定不低于120分;③甲、乙两人进行竞技比赛,甲的实力远胜于乙,在一次比赛中甲一定获胜;④当圆的半径变为原来的2倍时,圆的面积是原来的4倍.其中随机事件的个数是( )
A.1 B.3 C.0 D.4
2.(贵州省镇远县文德民族中学校2021届高三11月月考数学(理)试题)按文献记载,《百家姓》成文于北宋初年,表1记录了《百家姓》开头的24大姓氏:
表1
赵 钱 孙 李 周 吴 郑 王 冯 陈 褚 卫
蒋 沈 韩 杨 朱 秦 尤 许 何 吕 施 张
表2记录了2018年中国人口最多的前25大姓氏:
表2
1:李 2:王 3:张 4:刘 5:陈
6:杨 7:赵 8:黄 9:周 10:吴
11:徐 12:孙 13:胡 14:朱 15:高
16:林 17:何 18:郭 19:马 20:罗
21:梁 22:宋 23:郑 24:谢 25:韩
从《百家姓》开头的24大姓氏中随机选取1个姓氏,则该姓氏是2018年中国人口最多的前24大姓氏的概率为( )A. B. C. D.
3.(湖南省邵阳市邵东县第一中学2019-2020学年高二下学期第一次月考数学试题)下列说法错误的是( )
A.任一事件的概率总在内 B.不可能事件的概率一定为0
C.必然事件的概率一定为1 D.概率是随机的,在试验前不能确定
4.(2022·江西·南昌十中高一期中)甲、乙去同一家药店购买一种医用外科口罩,已知这家药店出售A,B,C三种医用外科口罩,甲、乙购买A,B,C三种医用口罩的概率分别如表:
购买A种医用口罩 购买B种医用口罩 购买C种医用口罩
甲 0.1 0.4
乙 0.3 0.2
则甲、乙购买的是同一种医用外科口罩的概率为( )
A.0.24 B.0.28 C.0.30 D.0.32
5.(10.1.2事件的关系和运算-2020-2021学年高一数学新教材配套学案(人教A版2019必修第二册))从1,2,3,…,7这7个数中任取两个数,其中:
①恰有一个是偶数和恰有一个是奇数;②至少有一个是奇数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数.
上述事件中,是对立事件的是( )
A.① B.②④ C.③ D.①③
6.(陕西省黄陵中学2016-2017学年高一(普通班)下学期期末考试数学试题)从某班学生中任意找出一人,如果该同学的身高小于160 cm的概率为0.2,该同学的身高在[160,175](单位:cm)内的概率为0.5,那么该同学的身高超过175 cm的概率为( )
A.0.2 B.0.3 C.0.7 D.0.8
7.(重庆市南开中学2020届高三下学期第九次教学质量检测数学(理)试题)据《孙子算经》中记载,中国古代诸侯的等级从低到高分为:男 子 伯,侯 公,共五级.若给有巨大贡献的3人进行封爵,假设每种封爵的可能性相等,则3人中恰好有两人被封同一等级的概率为( )
A. B. C. D.
8.(山东省德州市2019-2020学年高二下学期期末考试数学试题)甲、乙两队进行友谊赛,采取三局两胜制,每局都要分出胜负,根据以往经验,单局比赛中甲队获胜的概率为,设各局比赛相互间没有影响,则甲队战胜乙队的概率为( )
A. B. C. D.
多项选择题:本题共4小题,每小题满分5分,共20分. 在每小题给出的四个选项中,有多项符合题目要求。全部选对得5分,部分选对得2分,有选错的得0分.
9.下列命题中是真命题的是( )
A.做7次抛掷一枚均匀硬币的试验,结果有4次出现正面,因此出现正面的概率是
B.盒子中有大小均匀的3个黑球,2个白球,1个红球,则每种颜色被摸到的可能性相同
C.从-4,-3,-2,-1,0,1,2中任取一个数,取得小于0的概率大于取得不小于0的概率
D.分别从2名男生,2名女生中各选一名作为代表,则每名学生被选中的可能性相同
10.(第十章概率10.1随机事件与概率10.1.4概率的基本性质)黄种人群中各种血型的人所占的比例见下表:
血型 A B AB O
该血型的人所占比例 0.28 0.29 0.08 0.35
已知同种血型的人可以输血,O型血可以给任何一种血型的人输血,任何血型的人都可以给血型的人输血,其他不同血型的人不能互相输血,下列结论正确的是( )
A.任找一个人,其血可以输给B型血的人的概率是0.64
B.任找一个人,B型血的人能为其输血的概率是0.29
C.任找一个人,其血可以输给O型血的人的概率为1
D.任找一个人,其血可以输给型血的人的概率为1
11.(2021·河北保定·高一期末)以下结论不正确的是( )
A.对立事件一定互斥 B.事件A与事件B的和事件的概率一定大于事件A的概率
C.事件A与事件B互斥,则有 D.事件A,B满足,则A,B是对立事件
12.(2021·湖南·衡阳市八中高一期末)4支足球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.下列结论中正确的是( )
A.恰有四支球队并列第一名为不可能事件 B.有可能出现恰有三支球队并列第一名
C.恰有两支球队并列第一名的概率为 D.只有一支球队名列第一名的概率为
填空题:本题共4小题,每小题5分,共20分。
13.(2022·江西·景德镇一中高一期末)某次联欢会上设有一个抽奖游戏,抽奖箱中共有四种不同颜色且形状大小完全相同的小球16个,分别代表一等奖、二等奖、三等奖、无奖四种奖项.其中红球代表一等奖且只有1个,黄球代表三等奖,从中任取一个小球,若中二等奖或三等奖的概率为,小华同学获得一次摸奖机会,则求他不能中奖的概率是____________.
14.(2022·陕西·宝鸡市陈仓区教育体育局教学研究室高一期中)给出如下几个命题:
①若A是随机事件,则;
②若事件A与B是互斥事件,则A与B一定是对立事件;
③若事件A与B是对立事件,则A与B一定是互斥事件;
④事件A,B中至少有一个发生的概率一定比A,B中恰有一个发生的概率大.
其中正确的是___________.(填序号)
15.(2019年浙江省十校联盟高三上学期10月联考数学试题)1742年6月7日,哥德巴赫在给大数学家欧拉的信中提出:任一大于2的偶数都可写成两个质数的和.这就是著名的“哥德巴赫猜想”,可简记为“1+1”.1966年,我国数学家陈景润证明了“1+2”,获得了该研究的世界最优成果.若在不超过30的所有质数中,随机选取两个不同的数,则两数之和不超过30的概率是________.
16.(2018·山西·怀仁市第一中学校高一期末)口袋里装有1红,2白,3黄共6个形状相同的小球,从中取出2球,事件“取出的两球同色”,“取出的2球中至少有一个黄球”,“取出的2球至少有一个白球”,“取出的两球不同色”,“取出的2球中至多有一个白球”.下列判断中正确的序号为________.
①与为对立事件;②与是互斥事件;③与是对立事件:④;⑤.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(陕西省渭南市华州区咸林中学2021-2022学年高二下学期期中理科数学试题)甲 乙两人参加一次考试.已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题,规定每次考试都从各选题中随机抽出3题进行测试,至少答对2题才算合格.
(1)分别求甲 乙两人考试合格的概率;
(2)求甲 乙两人至少有一人考试合格的概率.
18.国家规定每年的月日以后的天为当年的暑假.某钢琴培训机构对位钢琴老师暑假一天的授课量进行了统计,如下表所示:
授课量(单位:小时)
频数
培训机构专业人员统计近年该校每年暑假天的课时量情况如下表:
课时量(单位:天)
频数
(同组数据以这组数据的中间值作代表)
(1)估计位钢琴老师一日的授课量的平均数;
(2)若以(1)中确定的平均数作为上述一天的授课量.已知当地授课价为元/小时,每天的各类生活成本为元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师天暑假授课利润不少于万元的概率.
19.某少儿游泳队需对队员进行限时的仰卧起坐达标测试;已知队员的测试分数与仰卧起坐
个数之间的关系如下:;测试规则:每位队员最多进行三组测试,
每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该
队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”
在一分钟内限时测试的频率分布直方图如下:
(1)计算值,并根据直方图计算“喵儿”1分钟内仰卧起坐的个数;
(2)计算在本次的三组测试中,“喵儿”得分等于的概率.
20.(陕西省2021届高三下学期第三次教学质量检测文科数学试题)统计某班级名学生数学期末考试成绩(单位:分)的频率频率分布直方图如图所示:
(1)分别求出成绩落在与中的学生人数;
(2)从成绩在和的学生中按照分层抽样的方法抽取人参加全校数学文化知识竞赛,如果有人获奖,求这人的成绩都在中的概率.
21.(2021·河北邯郸·高一期末)某市为了了解人们对“中国梦”的伟大构想的认知程度,针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(95分及以上为认知程度高),结果认知程度高的有人,按年龄分成5组,其中第一组:,第二组:,第三组:,第四组:,第五组:,得到如图所示的频率分布直方图,已知第一组有10人.
(1)根据频率分布直方图,估计这人的平均年龄和第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任本市的“中国梦”宣传使者.
(i)若有甲(年龄38),乙(年龄40)两人已确定人选宣传使者,现计划从第四组和第五组被抽到的使者中,再随机抽取2名作为组长,求甲、乙两人至少有一人被选上的概率;
(ii)若第四组宣传使者的年龄的平均数与方差分别为37和,第五组宣传使者的年龄的平均数与方差分别为43和1,据此估计这人中35~45岁所有人的年龄的方差.
22.(2020·山东·胶州市教育和体育局高一期末)有一种鱼的身体吸收汞,当这种鱼身体中的汞含量超过其体重的(即百万分之一)时,人食用它,就会对人体产生危害.现从一批该鱼中随机选出条鱼,检验鱼体中的汞含量与其体重的比值(单位:),数据统计如下:
(1)求上述数据的中位数、众数、极差,并估计这批鱼该项数据的分位数;
(2)有,两个水池,两水池之间有个完全相同的小孔联通,所有的小孔均在水下,且可以同时通过条鱼.
(ⅰ)将其中汞的含量最低的条鱼分别放入水池和水池中,若这条鱼的游动相互独立,均有的概率进入另一水池且不再游回,求这两条鱼最终在同一水池的概率;
(ⅱ)将其中汞的含量最低的条鱼都先放入水池中,若这条鱼均会独立地且等可能地从其中任意一个小孔由水池进入水池且不再游回水池,求这两条鱼由不同小孔进入水池的概率.
参考答案全解全析
1.B
【详解】
①②③均是可能发生也可能不发生的事件,为随机事件,
④是一定发生的事件,为必然事件.
则随机事件有个.
故选:B.
2.C
【详解】
因为从《百家姓》开头的24大姓氏中随机选取1个姓氏的基本事件共有24种,
2018年中国人口最多的前24大姓氏中《百家姓》开头的24大姓氏的基本事件有赵、孙、李、周、吴、郑、王、陈、杨、朱、何、张共有12种,
所以该姓氏是2018年中国人口最多的前24大姓氏的概率为概率为,
故选:C
3.D
解:任一事件的概率总在内,不可能事件的概率为0,必然事件的概率为1,概率是客观存在的,是一个确定值.
故选:D.
4.B
由概率的性质求得甲购买A口罩、乙购买B口罩的概率,再应用独立事件乘法公式和互斥事件加法公式求概率.
【详解】
由表知:甲购买A口罩概率为,乙购买B口罩概率为,
所以甲、乙购买同一种口罩的概率.
故选:B
5.C
【详解】
解析:③中“至少有一个是奇数”即“两个奇数或一奇一偶”,
而从1~7中任取两个数根据取到数的奇偶性可认为共有三件事件:
“两个都是奇数”“一奇一偶”“两个都是偶数”,
故“至少有一个是奇数”与“两个都是偶数”是对立事件,其余都不是对立事件.
故选:C
6.B
解:因为该同学的身高小于160cm的概率为0.2,该同学的身高在[160,175]cm的概率为0.5,和该同学的身高超过175cm的概率和为1,利用对立事件可知1-0.2-0.5=0.3,选B
7.D
【解析】
先由题意,确定3人封爵所包含的总的基本事件个数,再求出满足条件的基本事件个数,基本事件个数比,即可为所求概率.
【详解】
由题意,每个人被封爵都有5种情况,因此对3人封爵,共有种,
3人中恰好有两人被封同一等级共有种情况;
则3人中恰好有两人被封同一等级的概率为.
故选:D.
【点睛】
本题主要考查求古典概型的概率,属于常考题型.
8.C
【解析】
【分析】
甲队战胜乙队包含两种情况:①甲连胜2局,②前两局甲队一胜一负,第三局甲队胜,由此利用相互独立事件概率乘法公式和互斥事件概率加法公式能求出甲队战胜乙队的概率.
【详解】
甲、乙两队进行友谊赛,采取三局两胜制,每局都要分出胜负,
根据以往经验,单局比赛中甲队获胜的概率为,设各局比赛相互间没有影响,
甲队战胜乙队包含两种情况:
①甲连胜2局,概率为,
②前两局甲队一胜一负,第三局甲队胜,概率为,
则甲队战胜乙队的概率为.
故选:.
【点睛】
本题考查概率的求法,考查相互独立事件概率乘法公式和互斥事件概率加法公式等基础知识,考查推理能力与计算能力,是基础题.
9.CD
【解析】
【分析】
根据题意求出各试验事件发生的概率,逐一判断即可得出选项.
【详解】
解析:A中,抛掷一枚硬币出现正面的概率是,故错误;
B中,摸到黑球 白球 红球的可能性分别为,,,故错误,
C中,取得小于0的概率为,取得不小于0的概率为,故正确;
D中,每名学生被选中的可能性都为,故正确.
故选:CD.
10.AD
【解析】
根据输血的规则,可以输给B型血的人为B或O型;B型血的人可以输血给B型或血型;可以输给O型血的人只能是O型;所有人都可以输给型血的人.
【详解】
任找一个人,其血型为A、B、、O型血的事件分别记为、、、,它们两两互斥.
由已知,有,,,.因为B,O型血可以输给B型血的人,
所以“可以输给B型血的人”为事件,根据概率的加法公式,得,故A正确;
B型血的人能为B型、型的人输血,其概率为,B错误;
由O型血只能接受O型血的人输血知,C错误;
由任何人的血都可以够给型血的人,知D正确.
故选:AD.
【点睛】
此题考查互斥事件概率加法公式,关键在于弄清题意,此题应弄清楚可以输血的规则.
11.BCD
【解析】
【分析】
由对立事件与互斥事件的关系可判断A;由事件的包含关系可判断B;由对立事件的概率可判断C;由对立事件的定义可判断D.
【详解】
对于选项A:对立事件一定是互斥事件,故A正确;
对于选项B:当事件包含事件时,事件A与事件B的和事件的概率等于事件A的概率,故B错误;
对于选项C:当事件A与事件B对立时,则有,因为互斥事件不一定是对立事件,故C错误;
对于选项D:由对立事件的定义可知这种说法是错误的. 故D错误.
故选:BCD.
12.ABD
【解析】
【分析】
4支足球队进行单循环比赛总的比赛共有场比赛,比赛的所有结果共有种;
选项A,这6场比赛中不满足4支球队得分相同的的情况;
选项B,举特例说明即可;
选项C,在6场比赛中,从中选2支球队并列第一名有种可能,再分类计数相互获胜的可能数,最后由古典概型计算概率;
选项D,只有一支球队名列第一名,则该球队应赢了其他三支球队,由古典概型问题计算即可.
【详解】
4支足球队进行单循环比赛总的比赛共有场比赛,比赛的所有结果共有种;
选项A,这6场比赛中若4支球队优先各赢一场,则还有2场必然有2支或1支队伍获胜,那么所得分值不可能都一样,故是不可能事件,正确;
选项B,其中6场比赛中,依次获胜的可以是,此时3队都获得2分,并列第一名,正确;
选项C,在6场比赛中,从中选2支球队并列第一名有种可能,若选中a,b,其中第一类a赢b,有a,b,c,d,a,b和a,b,d,c,a,b两种情况,同理第二类b赢a,也有两种,故恰有两支球队并列第一名的概率为,错误;
选项D,从4支球队中选一支为第一名有4种可能;这一支球队比赛的3场应都赢,则另外3场的可能有种,故只有一支球队名列第一名的概率为,正确.
故选:ABD
【点睛】
本题考查利用计数原理解决实际问题的概率问题,还考查了事件成立与否的判定,属于较难题.
13.
【详解】
从个球中任取一个小球,中二等奖或三等奖的概率为,
故可得代表二等奖和三等奖的球共有个,又代表一等奖的球有个,
故代表无奖的球有个,故小华同学获得一次摸奖机会,不能中奖的概率.
故答案为:.
14.① ③
【解析】
【分析】
由几何概型中随机事件的发生概率可以为0或1,判断①;若事件A与B是对立事件,则A与B一定是互斥事件,但事件A与B是互斥事件,则A与B不一定是对立事件,判断②、③;当A与B的发生概率为0或A与B互斥时,则事件A,B中至少有一个发生的概率不一定与A,B中恰有一个发生的概率相同,判断④.
【详解】
若A是随机事件,则,在几何概型中随机事件的发生概率可以为0或1,故①正确;
但事件A与B是互斥事件,则A与B不一定是对立事件;例如掷一枚骰子“朝上的面为1”和“朝上的面为2”互斥但不对立,故②错误、
若事件A与B是对立事件,则A与B一定是互斥事件,互斥事件包含对立事件;故③正确;
事件A,B中至少有一个发生的概率不一定比A,B中恰有一个发生的概率大,如果A与B的发生概率为0或A与B互斥,则概率一样大,故④错误.
故答案为:① ③
15.
【解析】
【分析】
根据题意,利用列举法求出不超过30的所有质数,再利用古典概型的概率公式进行计算即可.
【详解】
根据题意可知,不共有超过30的所有质数有2,3,5,7,11,13,17,19,23,29共10个,从中选取2个不同的数有种,和超过30的共有15种,所以两数之和不超过30的概率是.
【点睛】
本题主要考查古典概型概率的求解.
16.①④
【解析】
【分析】
在①中,由对立事件定义得与为对立事件;有②中,与有可能同时发生;在③中,与有可能同时发生;在④中,(C)(E);在⑤中,从而(B)(C).
【详解】
口袋里装有1红,2白,3黄共6个形状相同小球,从中取出2球,
事件 “取出的两球同色”, “取出的2球中至少有一个黄球”,
“取出的2球至少有一个白球”, “取出的两球不同色”, “取出的2球中至多有一个白球”,
①,由对立事件定义得与为对立事件,故①正确;
②,与有可能同时发生,故与不是互斥事件,故②错误;
③,与有可能同时发生,不是对立事件,故③错误;
④,(C),(E),,
从而(C)(E),故④正确;
⑤,,从而(B)(C),故⑤错误.
故答案为:①④.
【点睛】
本题考查命题真假的判断,是基础题,考查对立互斥事件,解题时要认真审题,注意对立事件、互斥事件等基本概念的合理运用.
17.(1)甲 乙两人考试合格的概率分别为、;
(2).
【解析】
【分析】
(1)根据古典概型计算公式进行求解即可;
(2)根据(1)的结论,结合对立事件的概率公式进行求解即可.
(1)
设事件:甲考试合格,事件:乙考试合格,
所以,;
(2)
甲 乙两人至少有一人考试合格的概率为:.
18.(1)小时;(2).
【解析】
(1)将每组的中点值乘以频数,相加后除以可得出位老师暑假一日的授课量的平均数;
(2)设一位钢琴老师每年暑假天的授课天数为,计算出每位钢琴老师每日的利润,结合每位钢琴老师天暑假授课利润不少于万元求得的取值范围,再结合课时量频数表可得出所求事件的概率.
【详解】
(1)估计位老师暑假一日的授课量的平均数为小时;
(2)设每年暑假天的授课天数为,则利润为.
由,得.
一位老师暑假利润不少于万元,即授课天数不低于天,
又天暑假内授课天数不低于天的频率为.
预测一位老师天暑假授课利润不少于万元的概率为.
【点睛】
本题考查频数分布表的应用,考查平均数与概率的计算,考查数据处理能力,属于基础题.
19.(1)0.03;41个;(2)0.555.
【解析】
【分析】
(1)由可得,利用每个矩形的中点横坐标与该矩形的纵坐标相乘后求和,即可结果;(2)在本次的三组测试中,“喵儿”得分为事件A,则“喵儿”可能第一组得分,或者第二组得分,或者第三组得分,根据互斥事件的概率公式以及独立事件同时发生的概率公式可得结果.
【详解】
(1).
“喵儿”仰卧起坐的平均值为:(个)
(2)由直方图可知,“喵儿”的得分情况如下:
0 60 80 100
0.1 0.5 0.1
在本次的三组测试中,“喵儿”得80分为事件A,则“喵儿”可能第一组得80分,或者第二组得80
分,或者第三组得80分,则.
【点睛】
本题主要考查频率分布直方图的应用,以及互斥事件与独立事件的概率公式,属于中档题. 直方图的主要性质有:(1)直方图中各矩形的面积之和为;(2)组距与直方图纵坐标的乘积为该组数据的频率;(3)每个矩形的中点横坐标与该矩形的纵坐标相乘后求和可得平均值;(4)直观图左右两边面积相等处横坐标表示中位数.
20.(1)成绩落在中学生人数为,成绩落在中学生人数为;(2).
【解析】
【分析】
(1)根据频率分布直方图中所有矩形面积之和为求出实数的值,并计算出成绩落在与中的学生所占的频率,乘以可得结果;
(2)列出所有的基本事件,并确定事件“所抽的人的成绩都在中”所包含的基本事件数,利用古典概型的概率公式可求得所求事件的概率.
【详解】
(1)据直方图知组距为,由,解得,
成绩落在中学生人数为,
成绩落在中学生人数为;
(2)从成绩在和的学生中按照分层抽样的方法抽取人,成绩落在有人,成绩落在有人,
记成绩落在中的人为、,成绩落在中的人为、、、,
则从人选人的基本事件共有个:
、、、、、、、、、、、、、、.
其中人的成绩都在中的基本事件有6个.
故所求概率为.
【点睛】
方法点睛:求解古典概型概率的方法如下:
(1)列举法;
(2)列表法;
(3)数状图法;
(4)排列组合数的应用.
21.(1)32.25岁;37.5;(2)(i);(ii)10.
【解析】
【分析】
(1) 根据频率分布直方图,利用组中值乘以相应的频率,即可的这人的平均年龄;设第80百分位数为,计算从左到右频率和为或计算从右到左频率和为,即可求出;
(2)(i)由题意可得,第四组应抽取4人,记为,,,甲,第五组抽取2人,记为,乙,根据古典概型计算方法求解即可;
(ii)根据方差的计算原理计算合并后方差即可.
【详解】
解:(1)设这人的平均年龄为,则
(岁).
设第80百分位数为,
方法一:由,解得.
方法二:由,解得.
(2)(i)由题意得,第四组应抽取4人,记为,,,甲,第五组抽取2人,记为,乙,
对应的样本空间为:
,共15个样本点.
设事件“甲、乙两人至少一人被选上”,则
,共有9个样本点.
所以,.
(ii)设第四组、第五组的宣传使者的年龄的平均数分别为,,方差分别为,,
则,,,,
设第四组和第五组所有宣传使者的年龄平均数为,方差为.
则,
,
因此,第四组和第五组所有宣传使者的年龄方差为10,
据此,可估计这人中年龄在35~45岁的所有人的年龄方差约为10.
22.(1)中位数为;众数为;极差为;估计这批鱼该项数据的百分位数约为;(2)(ⅰ);(ⅱ).
【解析】
【分析】
(1)由中位数—排序后处于中间的数,如有两个数取其平均数;众数—出现频率最高的数、极差—最大数与最小数的差;百分比位数—数据集中有n个数:当np为整数时,当np不为整数时;即可求出对应值;(2) (ⅰ)记:“两鱼最终均在水池”; :“两鱼最终均在水池”求出概率,由它们的互斥性即可求得两条鱼最终在同一水池的概率;(ⅱ)记:“两鱼同时从第n个小孔通过”且鱼的游动独立,知,而10个事件互斥,则“两鱼同时从一个小孔通过”的概率即可求,它与“两条鱼由不同小孔通过”为互斥事件,进而求得其概率
【详解】
解:(1)由题意知,数据的中位数为
数据的众数为
数据的极差为
估计这批鱼该项数据的百分位数约为
(2)(ⅰ)记“两鱼最终均在水池”为事件,则
记“两鱼最终均在水池”为事件,则
∵事件与事件互斥,
∴两条鱼最终在同一水池的概率为
(ⅱ)记“两鱼同时从第一个小孔通过”为事件,“两鱼同时从第二个小孔通过”为
事件,依次类推;而两鱼的游动独立
∴
记“两条鱼由不同小孔进入水池”为事件,则与对立,又由事件,事件,互斥
∴
即
【点睛】
本题考查了数据特征值的概念,以及利用条件概率公式,结合互斥事件、独立事件等概念求概率;注意独立事件:多个事件的发生互不相关,且可以同时发生;互斥事件:一个事件发生则另一个事件必不发生,即不能同时发生
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
