北师大版数学八年级下册6.2 平行四边形的判定 同步练习(含答案)
文档属性
| 名称 | 北师大版数学八年级下册6.2 平行四边形的判定 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 396.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-18 08:23:47 | ||
图片预览


文档简介
北师大版八下 6.2 平行四边形的判定
一、选择题(共17小题)
1. 下面几组条件中,能判定一个四边形是平行四边形的是
A. 一组对边相等 B. 两条对角线互相平分
C. 一组对边平行 D. 两条对角线互相垂直
2. 如图,,点 在直线 上,点 , 在直线 上,,如果 ,,那么平行线 , 之间的距离为
A. B. C. D. 不能确定
3. 已知直线 ,点 在 上,点 ,, 在 上,且 ,,,则 与 之间的距离
A. 等于 B. 等于
C. 等于 D. 小于或等于
4. 点 ,, 是平面内不在同一条直线上的三点,点 是平面内任意一点,若 ,,, 四点恰能构成一个平行四边形,则在平面内符合这样条件的点 有
A. 个 B. 个 C. 个 D. 个
5. 如图,有 ,, 三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线
A. 户最长 B. 户最长 C. 户最长 D. 三户一样长
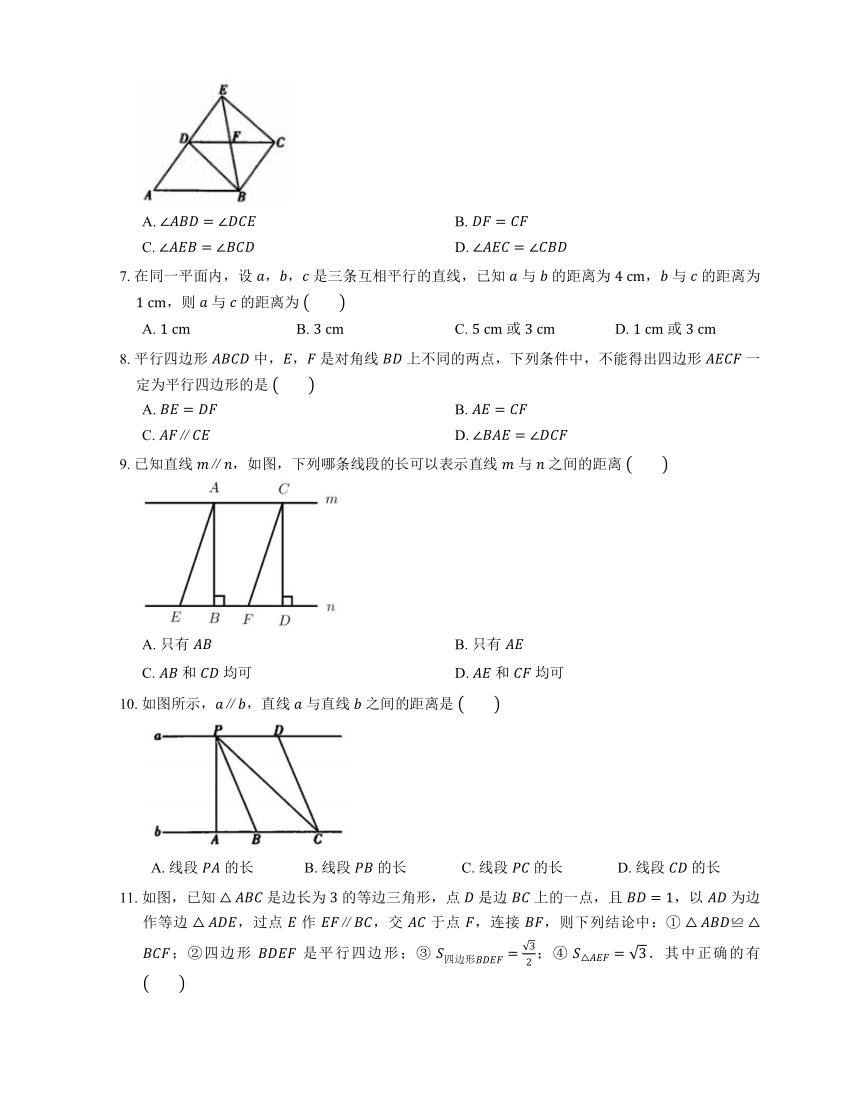
6. 如图, 是平行四边形 边 延长线上一点,连接 ,,, 交 于点 .添加以下条件,不能判定四边形 为平行四边形的是
A. B.
C. D.
7. 在同一平面内,设 ,, 是三条互相平行的直线,已知 与 的距离为 , 与 的距离为 ,则 与 的距离为
A. B. C. 或 D. 或
8. 平行四边形 中,, 是对角线 上不同的两点,下列条件中,不能得出四边形 一定为平行四边形的是
A. B.
C. D.
9. 已知直线 ,如图,下列哪条线段的长可以表示直线 与 之间的距离
A. 只有 B. 只有
C. 和 均可 D. 和 均可
10. 如图所示,,直线 与直线 之间的距离是
A. 线段 的长 B. 线段 的长 C. 线段 的长 D. 线段 的长
11. 如图,已知 是边长为 的等边三角形,点 是边 上的一点,且 ,以 为边作等边 ,过点 作 ,交 于点 ,连接 ,则下列结论中:① ;②四边形 是平行四边形;③ ;④ .其中正确的有
A. 个 B. 个 C. 个 D. 个
12. 下列命题中,说法正确的是
A. 所有菱形都相似
B. 两边对应成比例且有一组角对应相等的两个三角形相似
C. 三角形的重心到一个顶点的距离,等于它到这个顶点对边距离的两倍
D. 斜边和直角边对应成比例,两个直角三角形相似
13. 如图,若直线 ,则直线 , 之间的距离是
A. 线段 的长度 B. 线段 的长度
C. 线段 的长度 D. 线段 的长度
14. 在四边形 中,对角线 , 相交于点 ,给出下列四个条件:① ;② ;③ ;④ .从中任选两个条件,能使四边形 为平行四边形的选法有
A. 种 B. 种 C. 种 D. 种
15. 在同一平面内,已知 ,若直线 , 间的距离为 ,直线 , 间的距离为 ,则直线 , 间的距离是 .
A. B. C. 或 D. 不确定
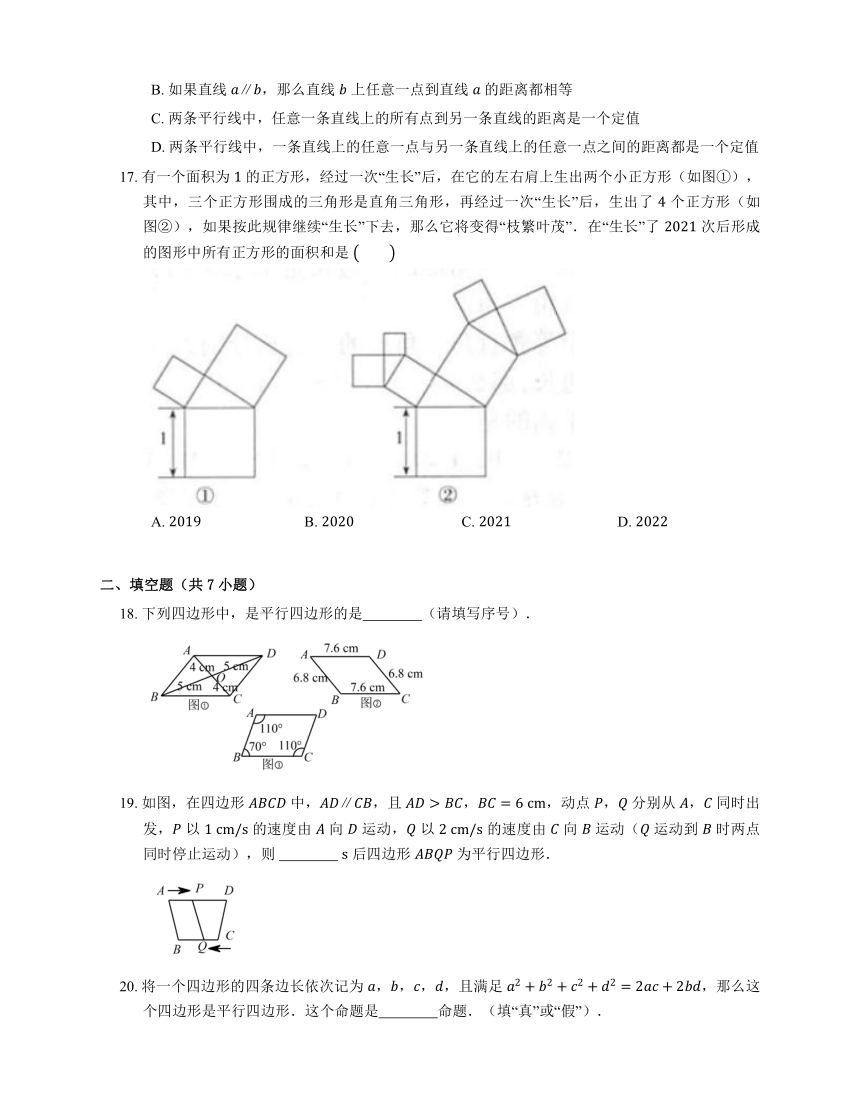
16. 如图,已知直线 ,小王在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离都是 ;小丁在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离 也都是 .该操作反映了平行线的某种性质,下列对该性质的描述中,不正确的是
A. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
B. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
C. 两条平行线中,任意一条直线上的所有点到另一条直线的距离是一个定值
D. 两条平行线中,一条直线上的任意一点与另一条直线上的任意一点之间的距离都是一个定值
17. 有一个面积为 的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图①),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了 个正方形(如图②),如果按此规律继续“生长”下去,那么它将变得“枝繁叶茂”.在“生长”了 次后形成的图形中所有正方形的面积和是
A. B. C. D.
二、填空题(共7小题)
18. 下列四边形中,是平行四边形的是 (请填写序号).
19. 如图,在四边形 中,,且 ,,动点 , 分别从 , 同时出发, 以 的速度由 向 运动, 以 的速度由 向 运动( 运动到 时两点同时停止运动),则 后四边形 为平行四边形.
20. 将一个四边形的四条边长依次记为 ,,,,且满足 ,那么这个四边形是平行四边形.这个命题是 命题.(填“真”或“假”).
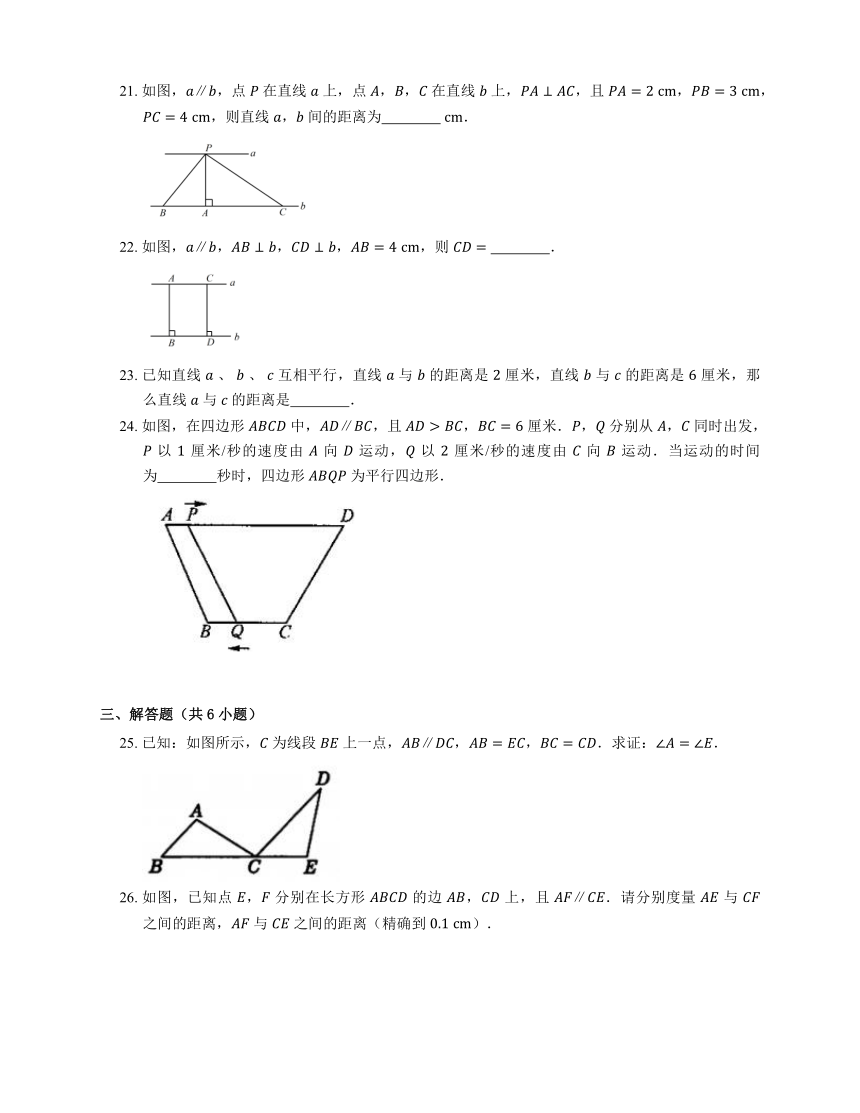
21. 如图,,点 在直线 上,点 ,, 在直线 上,,且 ,,,则直线 , 间的距离为 .
22. 如图,,,,,则 .
23. 已知直线 、 、 互相平行,直线 与 的距离是 厘米,直线 与 的距离是 厘米,那么直线 与 的距离是 .
24. 如图,在四边形 中,,且 , 厘米., 分别从 , 同时出发, 以 厘米/秒的速度由 向 运动, 以 厘米/秒的速度由 向 运动.当运动的时间为 秒时,四边形 为平行四边形.
三、解答题(共6小题)
25. 已知:如图所示, 为线段 上一点,,,.求证:.
26. 如图,已知点 , 分别在长方形 的边 , 上,且 .请分别度量 与 之间的距离, 与 之间的距离(精确到 ).
27. 若两个角的两边分别垂直,其中一个角比另一个角的 倍少 ,求这两个角的度数.
28. 如图,已知 为平行四边形 的边 上的任一点, 延长线交 延长线于点 .试说明 的理由.
29. 如图,平面四边形 的对角线 , 相交于点 ,, 分别是 , 的中点,连接 ,.
(1)根据题意,补全图形;
(2)求证:.
30. 如图,已知四边形 是平行四边形, 于点 , 于点 ,延长 , 分别交 , 于点 ,.
(1)求证:四边形 是平行四边形;
(2)已知 ,,求 的长.
答案
1. B
2. B
3. D
4. C
【解析】过 ,, 三点作对边的平行线
5. D
6. C
【解析】 四边形 是平行四边形,
,,
,,
,
,
,
四边形 为平行四边形,故A正确;
,
,在 与 中,
,
,
,
四边形 为平行四边形,故B正确;
,
,
,
,
,同理 ,
不能判定四边形 为平行四边形,故C错误;
,
.
,
,
四边形 为平行四边形,故D正确.故选C.
7. C
【解析】当直线 在 , 之间时,
因为 ,, 是三条互相平行的直线, 与 的距离为 , 与 的距离 ,
所以 与 的距离为 ();
当直线 不在 , 之间时,
因为 ,, 是三条互相平行的直线, 与 的距离为 , 与 的距离为 ,
所以 与 的距离为 ().
综上所述, 与 的距离为 或 .
8. B
【解析】A.如图,
四边形 是平行四边形,
,,
,
,
四边形 是平行四边形,故不符合题意;
B.如图所示,,不能得到四边形 是平行四边形,故符合题意;
C.如图,
四边形 是平行四边形,
,
,
,
又 ,
,
,
且 ,
四边形 是平行四边形,故不符合题意;
D.如图,
四边形 是平行四边形,
,,
,
又 ,
,
,,
,
,
且 ,
四边形 是平行四边形,故不符合题意.
9. C
【解析】,
在同一平面内,垂直于 的线段,也垂直于 ,且该线段可表示 , 的最短距离.
故 , 可表示 , 的距离.
10. A
【解析】由题图可得,直线 与直线 之间的距离是线段 的长,故选A.
11. C
【解析】连接 ,作 于点 .
, 都是等边三角形,
,,,
,
,
,,
,
,
是等边三角形,,
,
,
四边形 是平行四边形,故②正确;
,,,
,故①正确;
,故③正确;,故④错误.
12. D
13. B
【解析】由直线 ,,得线段 的长度是直线 , 之间的距离.
14. B
15. C
16. D
17. D 【解析】设正方形 ,, 围成的直角三角形的三条边长分别是 ,,.
如图,
根据勾股定理,得 ,
一次“生长”后,.
第二次“生长”后,,
推而广之,“生长”了 次后形成的图形中所有的正方形的面积和是 .
18. ①②③
19.
【解析】设 后四边形 为平行四边形,则 ,,,
四边形 是平行四边形,
所以 ,
所以 ,
所以 .
所以 后四边形 是平行四边形.
20. 真
21.
22.
23. 厘米或 厘米
24.
25. ,
,
在 和 中,
,
(全等三角形的对应角相等).
26. 过点 作 于点 .
经测量可得:,,则 与 之间的距离是 , 与 之间的距离是 .
27. 设另一个角的度数为 ,则这个角的度数是 .
因为两个角的两边分别垂直,
所以
解得
所以 或 .
故这两个角的度数分别是 , 或 ,.
28. 提示:连接 ,
因为 ,
所以 ,
因为 ,
所以 ,
所以 ,
所以 .
29. (1) 略.
(2) 四边形 是平行四边形,对角线 , 交于点 ,
,.
又 , 分别是 , 的中点,
,,
.
在 与 中,
,
.
30. (1) 四边形 是平行四边形,
,
,,
,
四边形 是平行四边形.
(2) 四边形 是平行四边形,
,
,
,
,
,
,
,
,
在 中,.
一、选择题(共17小题)
1. 下面几组条件中,能判定一个四边形是平行四边形的是
A. 一组对边相等 B. 两条对角线互相平分
C. 一组对边平行 D. 两条对角线互相垂直
2. 如图,,点 在直线 上,点 , 在直线 上,,如果 ,,那么平行线 , 之间的距离为
A. B. C. D. 不能确定
3. 已知直线 ,点 在 上,点 ,, 在 上,且 ,,,则 与 之间的距离
A. 等于 B. 等于
C. 等于 D. 小于或等于
4. 点 ,, 是平面内不在同一条直线上的三点,点 是平面内任意一点,若 ,,, 四点恰能构成一个平行四边形,则在平面内符合这样条件的点 有
A. 个 B. 个 C. 个 D. 个
5. 如图,有 ,, 三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线
A. 户最长 B. 户最长 C. 户最长 D. 三户一样长
6. 如图, 是平行四边形 边 延长线上一点,连接 ,,, 交 于点 .添加以下条件,不能判定四边形 为平行四边形的是
A. B.
C. D.
7. 在同一平面内,设 ,, 是三条互相平行的直线,已知 与 的距离为 , 与 的距离为 ,则 与 的距离为
A. B. C. 或 D. 或
8. 平行四边形 中,, 是对角线 上不同的两点,下列条件中,不能得出四边形 一定为平行四边形的是
A. B.
C. D.
9. 已知直线 ,如图,下列哪条线段的长可以表示直线 与 之间的距离
A. 只有 B. 只有
C. 和 均可 D. 和 均可
10. 如图所示,,直线 与直线 之间的距离是
A. 线段 的长 B. 线段 的长 C. 线段 的长 D. 线段 的长
11. 如图,已知 是边长为 的等边三角形,点 是边 上的一点,且 ,以 为边作等边 ,过点 作 ,交 于点 ,连接 ,则下列结论中:① ;②四边形 是平行四边形;③ ;④ .其中正确的有
A. 个 B. 个 C. 个 D. 个
12. 下列命题中,说法正确的是
A. 所有菱形都相似
B. 两边对应成比例且有一组角对应相等的两个三角形相似
C. 三角形的重心到一个顶点的距离,等于它到这个顶点对边距离的两倍
D. 斜边和直角边对应成比例,两个直角三角形相似
13. 如图,若直线 ,则直线 , 之间的距离是
A. 线段 的长度 B. 线段 的长度
C. 线段 的长度 D. 线段 的长度
14. 在四边形 中,对角线 , 相交于点 ,给出下列四个条件:① ;② ;③ ;④ .从中任选两个条件,能使四边形 为平行四边形的选法有
A. 种 B. 种 C. 种 D. 种
15. 在同一平面内,已知 ,若直线 , 间的距离为 ,直线 , 间的距离为 ,则直线 , 间的距离是 .
A. B. C. 或 D. 不确定
16. 如图,已知直线 ,小王在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离都是 ;小丁在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离 也都是 .该操作反映了平行线的某种性质,下列对该性质的描述中,不正确的是
A. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
B. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
C. 两条平行线中,任意一条直线上的所有点到另一条直线的距离是一个定值
D. 两条平行线中,一条直线上的任意一点与另一条直线上的任意一点之间的距离都是一个定值
17. 有一个面积为 的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图①),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了 个正方形(如图②),如果按此规律继续“生长”下去,那么它将变得“枝繁叶茂”.在“生长”了 次后形成的图形中所有正方形的面积和是
A. B. C. D.
二、填空题(共7小题)
18. 下列四边形中,是平行四边形的是 (请填写序号).
19. 如图,在四边形 中,,且 ,,动点 , 分别从 , 同时出发, 以 的速度由 向 运动, 以 的速度由 向 运动( 运动到 时两点同时停止运动),则 后四边形 为平行四边形.
20. 将一个四边形的四条边长依次记为 ,,,,且满足 ,那么这个四边形是平行四边形.这个命题是 命题.(填“真”或“假”).
21. 如图,,点 在直线 上,点 ,, 在直线 上,,且 ,,,则直线 , 间的距离为 .
22. 如图,,,,,则 .
23. 已知直线 、 、 互相平行,直线 与 的距离是 厘米,直线 与 的距离是 厘米,那么直线 与 的距离是 .
24. 如图,在四边形 中,,且 , 厘米., 分别从 , 同时出发, 以 厘米/秒的速度由 向 运动, 以 厘米/秒的速度由 向 运动.当运动的时间为 秒时,四边形 为平行四边形.
三、解答题(共6小题)
25. 已知:如图所示, 为线段 上一点,,,.求证:.
26. 如图,已知点 , 分别在长方形 的边 , 上,且 .请分别度量 与 之间的距离, 与 之间的距离(精确到 ).
27. 若两个角的两边分别垂直,其中一个角比另一个角的 倍少 ,求这两个角的度数.
28. 如图,已知 为平行四边形 的边 上的任一点, 延长线交 延长线于点 .试说明 的理由.
29. 如图,平面四边形 的对角线 , 相交于点 ,, 分别是 , 的中点,连接 ,.
(1)根据题意,补全图形;
(2)求证:.
30. 如图,已知四边形 是平行四边形, 于点 , 于点 ,延长 , 分别交 , 于点 ,.
(1)求证:四边形 是平行四边形;
(2)已知 ,,求 的长.
答案
1. B
2. B
3. D
4. C
【解析】过 ,, 三点作对边的平行线
5. D
6. C
【解析】 四边形 是平行四边形,
,,
,,
,
,
,
四边形 为平行四边形,故A正确;
,
,在 与 中,
,
,
,
四边形 为平行四边形,故B正确;
,
,
,
,
,同理 ,
不能判定四边形 为平行四边形,故C错误;
,
.
,
,
四边形 为平行四边形,故D正确.故选C.
7. C
【解析】当直线 在 , 之间时,
因为 ,, 是三条互相平行的直线, 与 的距离为 , 与 的距离 ,
所以 与 的距离为 ();
当直线 不在 , 之间时,
因为 ,, 是三条互相平行的直线, 与 的距离为 , 与 的距离为 ,
所以 与 的距离为 ().
综上所述, 与 的距离为 或 .
8. B
【解析】A.如图,
四边形 是平行四边形,
,,
,
,
四边形 是平行四边形,故不符合题意;
B.如图所示,,不能得到四边形 是平行四边形,故符合题意;
C.如图,
四边形 是平行四边形,
,
,
,
又 ,
,
,
且 ,
四边形 是平行四边形,故不符合题意;
D.如图,
四边形 是平行四边形,
,,
,
又 ,
,
,,
,
,
且 ,
四边形 是平行四边形,故不符合题意.
9. C
【解析】,
在同一平面内,垂直于 的线段,也垂直于 ,且该线段可表示 , 的最短距离.
故 , 可表示 , 的距离.
10. A
【解析】由题图可得,直线 与直线 之间的距离是线段 的长,故选A.
11. C
【解析】连接 ,作 于点 .
, 都是等边三角形,
,,,
,
,
,,
,
,
是等边三角形,,
,
,
四边形 是平行四边形,故②正确;
,,,
,故①正确;
,故③正确;,故④错误.
12. D
13. B
【解析】由直线 ,,得线段 的长度是直线 , 之间的距离.
14. B
15. C
16. D
17. D 【解析】设正方形 ,, 围成的直角三角形的三条边长分别是 ,,.
如图,
根据勾股定理,得 ,
一次“生长”后,.
第二次“生长”后,,
推而广之,“生长”了 次后形成的图形中所有的正方形的面积和是 .
18. ①②③
19.
【解析】设 后四边形 为平行四边形,则 ,,,
四边形 是平行四边形,
所以 ,
所以 ,
所以 .
所以 后四边形 是平行四边形.
20. 真
21.
22.
23. 厘米或 厘米
24.
25. ,
,
在 和 中,
,
(全等三角形的对应角相等).
26. 过点 作 于点 .
经测量可得:,,则 与 之间的距离是 , 与 之间的距离是 .
27. 设另一个角的度数为 ,则这个角的度数是 .
因为两个角的两边分别垂直,
所以
解得
所以 或 .
故这两个角的度数分别是 , 或 ,.
28. 提示:连接 ,
因为 ,
所以 ,
因为 ,
所以 ,
所以 ,
所以 .
29. (1) 略.
(2) 四边形 是平行四边形,对角线 , 交于点 ,
,.
又 , 分别是 , 的中点,
,,
.
在 与 中,
,
.
30. (1) 四边形 是平行四边形,
,
,,
,
四边形 是平行四边形.
(2) 四边形 是平行四边形,
,
,
,
,
,
,
,
,
在 中,.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
